考虑时变啮合刚度的船用高速斜齿轮动力学特性分析

文建爽，杜进辅，刘 凯，王峥嵘

(西安理工大学机械与精密仪器工程学院，陕西西安710048)

dynamics

斜齿轮由于承载能力大、传动平稳、易于加工和调整等优点，在航空、船舶、汽车和工业减速器等领域中获得了广泛应用，其动态啮合性能对机械设备整机可靠性、稳定性和振动噪声等特性影响显著。因此，斜齿轮传动的动力学特性一直是国内外学者的研究热点[1-3]。早期研究中，一般以平均啮合刚度代替时变啮合刚度[4]；后来，随着改进的材料力学法[5]以及基于LTCA[6]的时变啮合刚度计算方法的提出，学者们开始关注时变啮合刚度对齿轮传动动态性能的影响[7-9]。朱增宝、朱如鹏等[10]建立了采用双齿联轴器的人字齿行星传动系统动力学模型，从动载特性方面分析了时变啮合刚度对人字齿振动特性的影响；张柳等[11]从时域和频域方面着重分析了时变啮合刚度和齿距误差对斜齿轮振动特性的影响；王燕等[12]在系统振动微分方程的平衡位置处对其进行线性化处理，并利用多尺度法获得了系统振动稳定的边界条件，进而分析了时变啮合刚度对斜齿轮系统振动稳定性的影响。

但上述研究大都针对中低转速条件，所获得的结论是否适合高转速情况尚待验证。随着现代工业的高速发展，高速重载齿轮传动的需求也日益增多，对齿轮传动高转速、大载荷、高寿命等方面的要求也日益严格，许多工业领域的齿轮往往工作在过共振区，如直升机、船舰及电动汽车等领域的部分斜齿轮传动其转速已达到10 000 rpm以上。可见，研究高转速条件下斜齿轮传动的动力学特性具有重要意义。

为此，本文以某船用高速斜齿轮传动系统为研究对象，建立了6自由度弯-扭-轴耦合动力学模型，基于LTCA获得时变啮合刚度曲线，研究转速变化对系统振动特性的影响，并通过分析不同时变啮合刚度激励下，齿轮副啮合线方向振动加速度的时、频域结果，研究时变啮合刚度的均值和波动幅值对系统振动的影响，以期获得具有理论意义和实际应用价值的成果，为高速斜齿轮传动的设计和应用提供参考依据。

1 斜齿轮副弯-扭-轴动力学模型

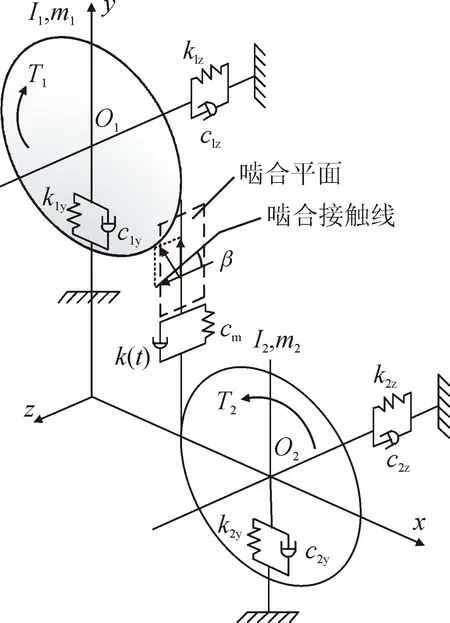
图1 斜齿轮弯-扭-轴动力学模型Fig.1 Bend-torsion-shaft dynamic model of helical gear

采用集中质量法建立6自由度斜齿轮传动的弯-扭-轴耦合动力学模型[13]，见图1。该系统的广义位移矩阵可表示为：

{δ}={y1,z1,θ1,y2,z2,θ2}T

(1)

式中：yi、zi、θi(i=1，2)分别表示主、从动斜齿轮中心在径向、轴向振动位移及转角位移。根据牛顿第二定律列出图1所示动力学模型的微分方程组见式(2)。

(2)

基于力、位移分解，将该系统中切向动态啮合力和轴向动态啮合力以参数形式表达如下：

式中：m1、m2分别为主、从动轮质量；Rb1、Rb2分别为主、从动轮基圆半径；β为斜齿轮螺旋角；α为压力角；T1、T2分别为主、从动轮转矩；y1、y2分别为主、从动轮中心在y方向的振动位移；z1、z2分别为主、从动轮中心在z方向的振动位移；θ1、θ2分别为主、从动轮的扭转振动位移；k1y、k2y分别为主、从动轮在y方向的等效支承刚度；k1z、k2z分别为主、从动轮在z方向的等效支承刚度；c1y、c2y分别为主、从动轮在方y向的等效支承阻尼；c1z、c2z分别为主、从动轮在z方向的等效支承阻尼；k(t)为齿轮时变啮合刚度；cm为啮合阻尼，其计算公式如下：

(4)

式中，ξ为阻尼比，本文取0.1。

为了消除齿轮刚体转角位移对后续分析的影响，引入相对转角位移q将转角位移转化为线位移，其表达式为：

q=Rb1θ1-Rb2θ2

(5)

将式(5)代入式(2)中，扭转振动方程可化简为：

(6)

式中，me为齿轮副的等效扭转质量：

(7)

2 时变啮合刚度的计算

本文采用基于LTCA的方法计算齿轮副时变啮合刚度，该方法以将齿轮几何分析和力学分析有机地结合在一起的LTCA为基础，可以得到齿轮副在修形和误差条件下的啮合刚度曲线。啮合刚度k(t)的计算式如下：

(8)

式中：P为力或力矩；Z为线位移或角位移变形。

通过LTCA可获得齿面载荷分布P和在当前接触位置载荷P作用下的线位移传动误差Z。Z主要由几何传动误差、轮齿弯曲变形和齿面接触变形引起。

几何传动误差与载荷P大小无关，由齿面设计和加工决定。当齿轮副材料、几何参数及啮合位置一定时，轮齿弯曲变形和接触变形由载荷P决定，可以根据美国格里森公司的计算方法得到[14]。各组成部分与载荷P的关系如下：

(9)

式中：c1,c2,c3为常数；δ1,δ2,δ3分别表示几何传动误差、轮齿弯曲变形和接触变形。

将一个啮合周期进行n等分，Zk(P)表示第k(k=1,2,…,n)个啮合位置在名义载荷P作用下的承载变形，可由轮齿LTCA程序得到[15]。

综上所述，可以得到第k个啮合位置在名义载荷P作用下的承载变形：

(10)

用待定系数法，进行三次不同载荷下的运算，便可确定系数c1,c2,c3，得到齿轮副不同啮合位置的载荷与变形的函数关系式。通过这个关系式，可以确定任意载荷下该位置的啮合刚度，对每一个啮合位置均进行上述运算，即可得到齿轮副整个啮合周期各啮合位置的啮合刚度，进而得到齿轮副的啮合刚度曲线。

3 算 例

表1为某船用高速斜齿轮副参数，其三维模型见图2。

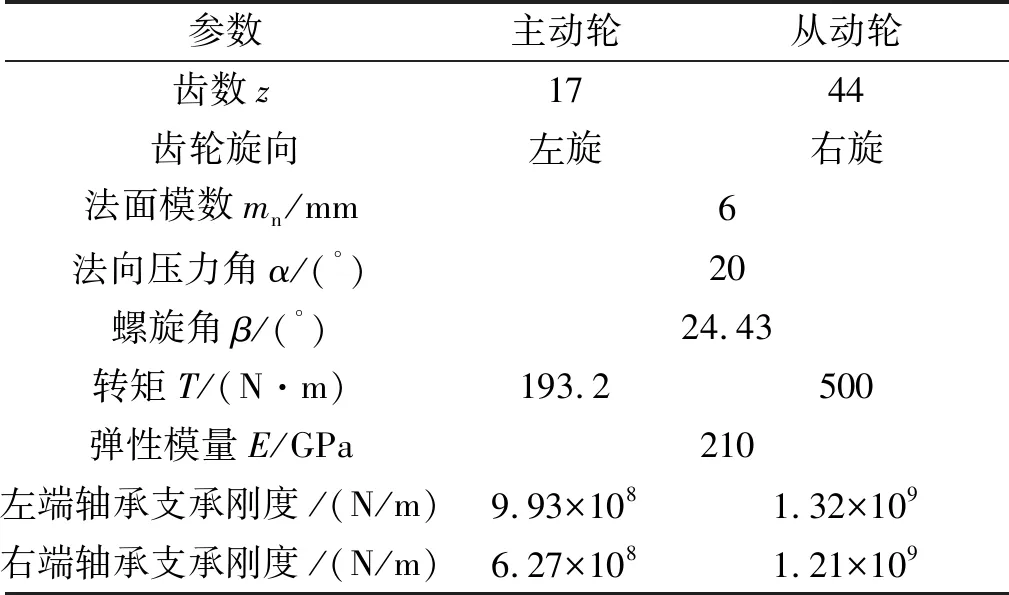
表1 齿轮副基本参数

图2 某斜齿轮三维模型Fig.2 3D model of a helical gear

根据前文方法，得到其在500 N·m负载下的时变啮合刚度曲线见图3。

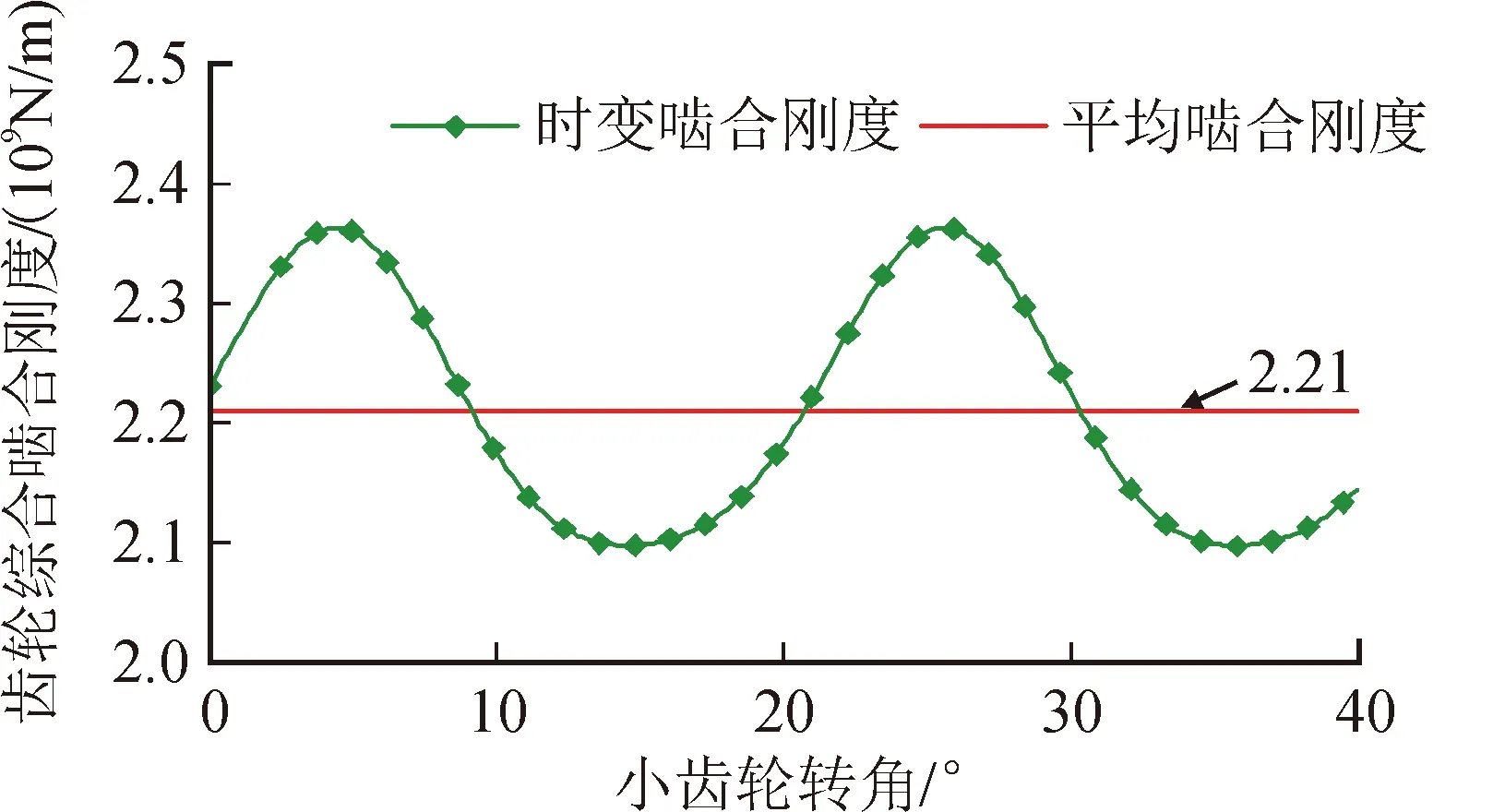
图3 齿轮综合啮合刚度曲线Fig.3 Gear comprehensive meshing stiffness curve

以斜齿轮副端面啮合线方向的相对振动加速度a作为主要指标考查系统振动程度，其表达式为：

(11)

将求解动力学模型得到的各方向振动加速度按照式(11)合成，并求出其均方根值。接着依次求出各转速下的相对振动加速度均方根值，绘制如图4所示的时变啮合刚度激励下的齿轮端面啮合线方向振动-转速图。

图4 齿轮啮合线方向振动-转速图Fig.4 Gear vibration-rotation speed diagram of meshing direction

图4可以看出，在时变啮合刚度曲线激励不变的情况下，不同转速下系统振动程度不同；除去共振峰外的加速度均方根值并未随转速升高而明显升高。这是由于时变啮合刚度作为一种参数激励，其本身的均值及幅值与转速无关。也即，只考虑时变啮合刚度激励情况下，远离共振转速时，转速升高对系统振动特性的影响不显著。在1/3和1/2共振转速N0处，发生了明显的超谐波共振。

为了研究齿轮平均啮合刚度对系统振动的影响，基于图2所示时变啮合刚度，取0.6倍、0.8倍、1.0倍、1.2倍、1.4倍五种不同平均啮合刚度(幅值不变，见图5)作为系统激励。求得系统啮合线方向振动加速度情况，见图6。

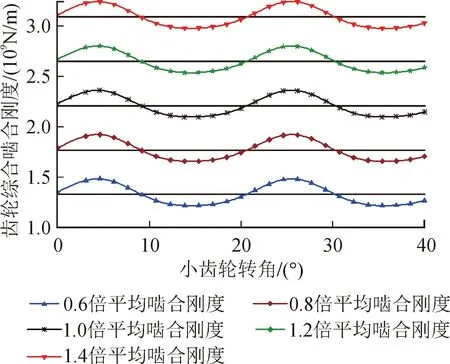
图5 不同平均刚度值的啮合刚度曲线Fig.5 Meshing stiffness curve of different means of stiffness

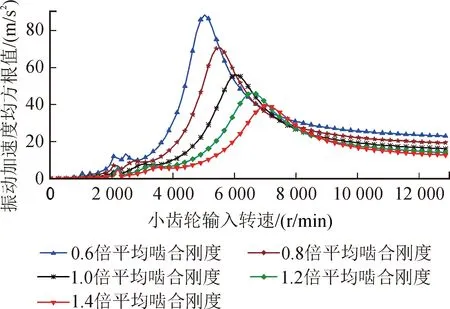
图6 不同平均啮合刚度下的振动-转速图Fig.6 Vibration-rotation speed diagram of the different means of stiffness

图6中，在齿轮时变啮合刚度幅值不变的情况下，除去共振峰值外，齿轮相对振动加速度均方根值随着齿轮平均啮合刚度的升高而降低，且系统固有频率发生了改变，齿轮副共振转速随齿轮平均啮合刚度的增大而增大。进一步分析得，平均啮合刚度减小使系统振动加速度均方根值相对于转速的变化率变大，这导致齿轮转速达到共振转速附近时齿轮振动系统稳定性变差。

图7～8分别为转速9 000 r/min、12 000 r/min时5种不同平均啮合刚度下啮合线方向振动时域图。

图7 9 000 r/min时不同平均刚度下啮合线方向振动时域图Fig.7 Time domain diagram of meshing direction vibration under different means of stiffness at 9 000 r/min

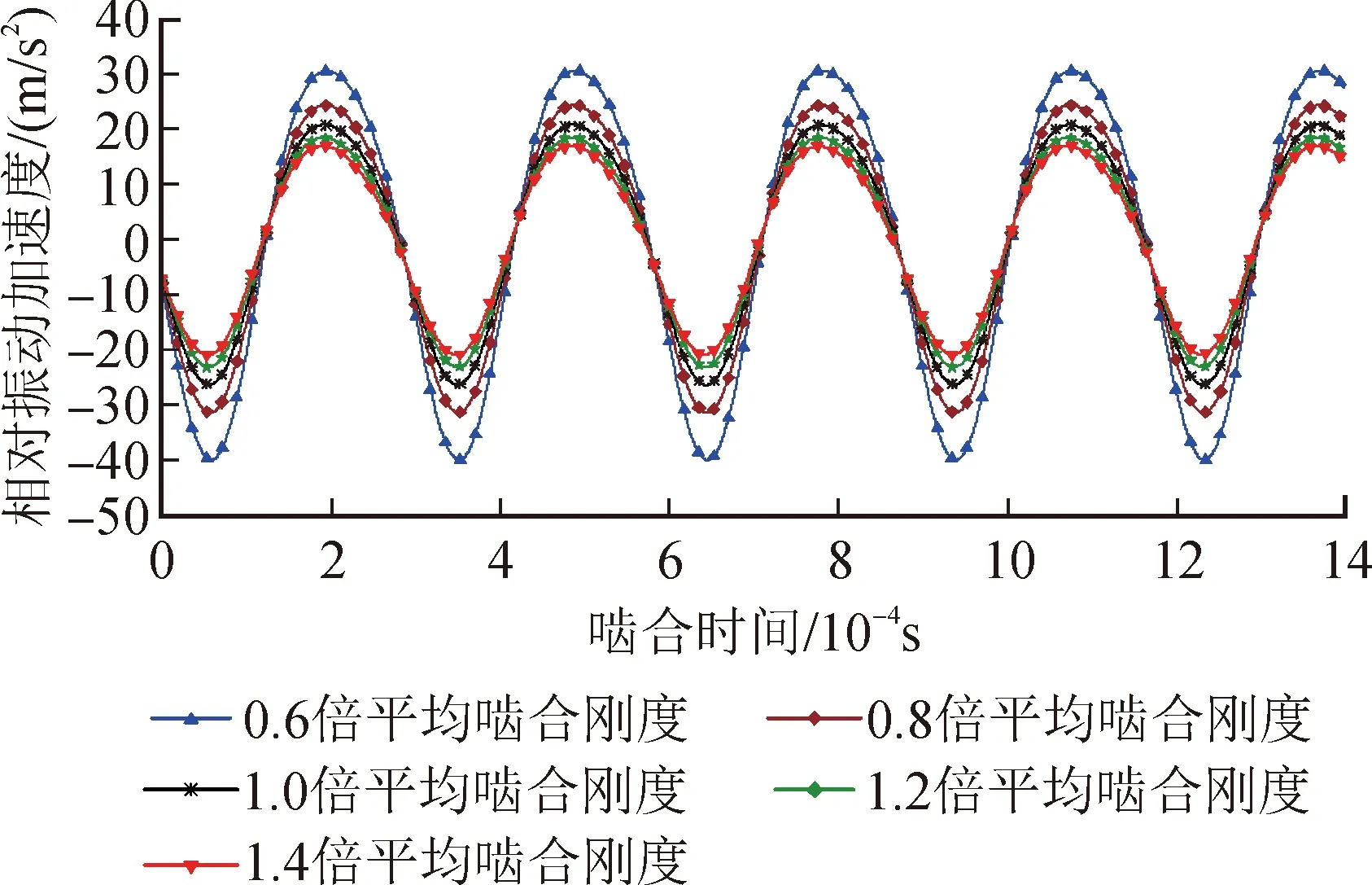
图8 12 000 r/min时不同平均刚度下啮合线方向振动时域图Fig.8 Time domain diagram of meshing direction vibration under different means of stiffness at 12 000 r/min

图9～10为频域图。

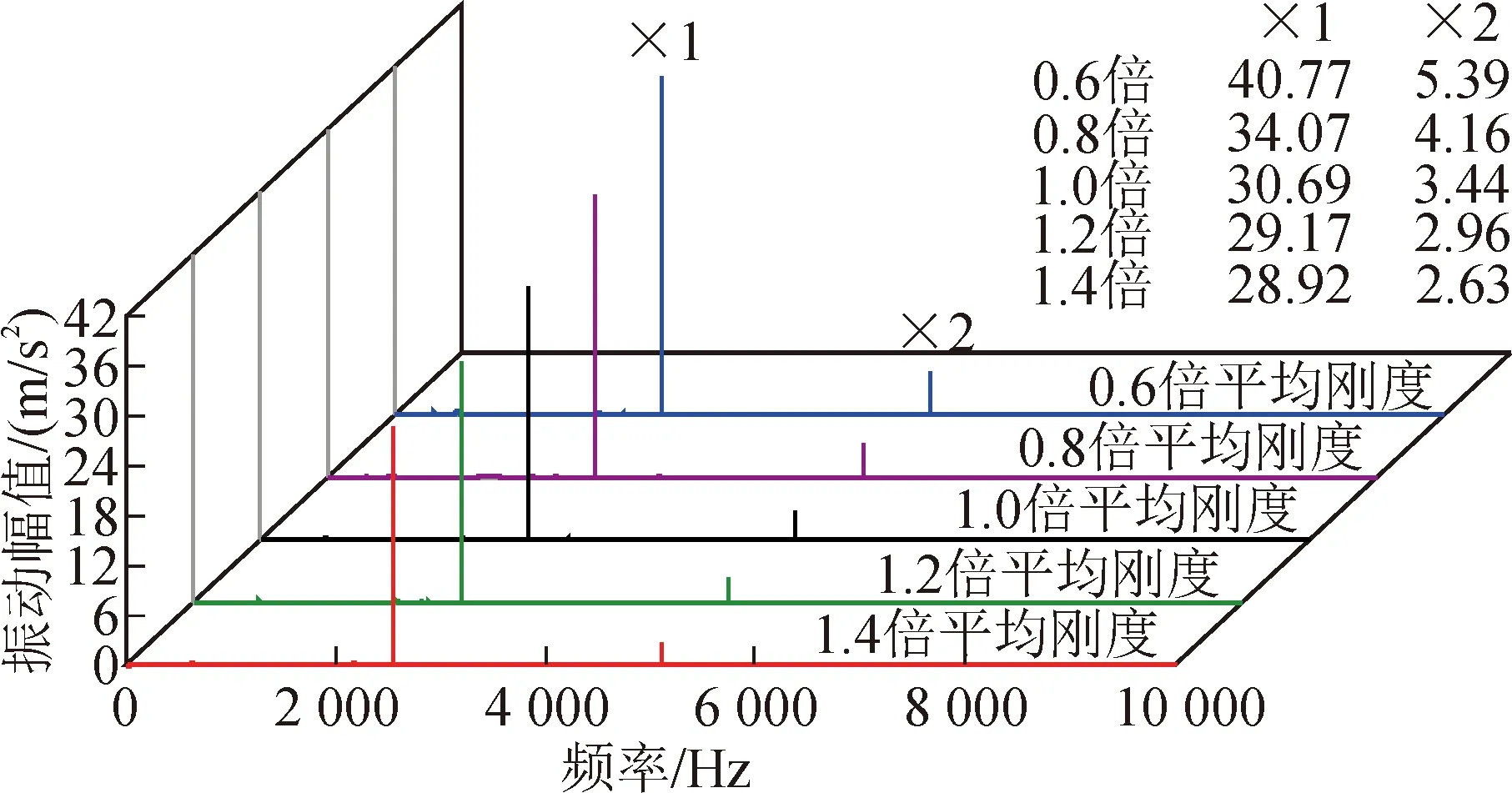
图9 9 000 r/min时不同平均刚度下啮合线方向振动频域图Fig.9 Frequency domain diagram of meshing direction vibration under different stiffness means at 9 000 r/min

图10 12 000 r/min不同平均刚度下啮合线方向振动频域图Fig.10 Frequency domain diagram of meshing direction vibration under different stiffness means at 12 000 r/min

由图7～10可得，平均啮合刚度越大，齿轮振动幅值越大，与图6得到的结论一致。

时变啮合刚度的幅值波动大小是影响齿轮系统振动响应的重要因素。为了研究时变啮合刚度对齿轮系统振动响应的影响，基于图2所示时变啮合刚度，取0.6倍、0.8倍、1.0倍、1.2倍、1.4倍五种不同幅值(平均啮合刚度值和周期保持不变，见图11)，作为系统激励输入动力学模型。求得系统啮合线方向振动加速度情况，见图12。

图11 不同幅值的啮合刚度曲线Fig.11 Meshing stiffness curves of different amplitudes

由图12得， 在齿轮平均啮合刚度不变的情况下，啮合刚度的幅值越大齿轮端面啮合线方向振动均方根值越大；且啮合刚度的幅值波动变化并未造成共振转速发生变化；时变啮合刚度幅值增大会使振动加速度均方根值相对于转速的变化率变大，如前所述，这会导致齿轮转速达到共振转速附近时系统稳定性变差。

图12 不同啮合刚度幅值下的振动-转速图Fig.12 Vibration-rotation speed diagram under different amplitudes of meshing stiffness

图13～14分别为转速9 000 r/min、12 000 r/min时5种不同时变啮合刚度幅值下啮合线方向振动时域图，其频域图见图15～16。由图13～16可得，啮合刚度幅值越大，齿轮振动幅值越大。与分析图12得到的结论一致。

图13 9 000 r/min时不同幅值波动下啮合线方向振动时域图Fig.13 Time domain diagram of meshing direction vibration under different amplitudes of meshing stiffness at 9 000 r/min

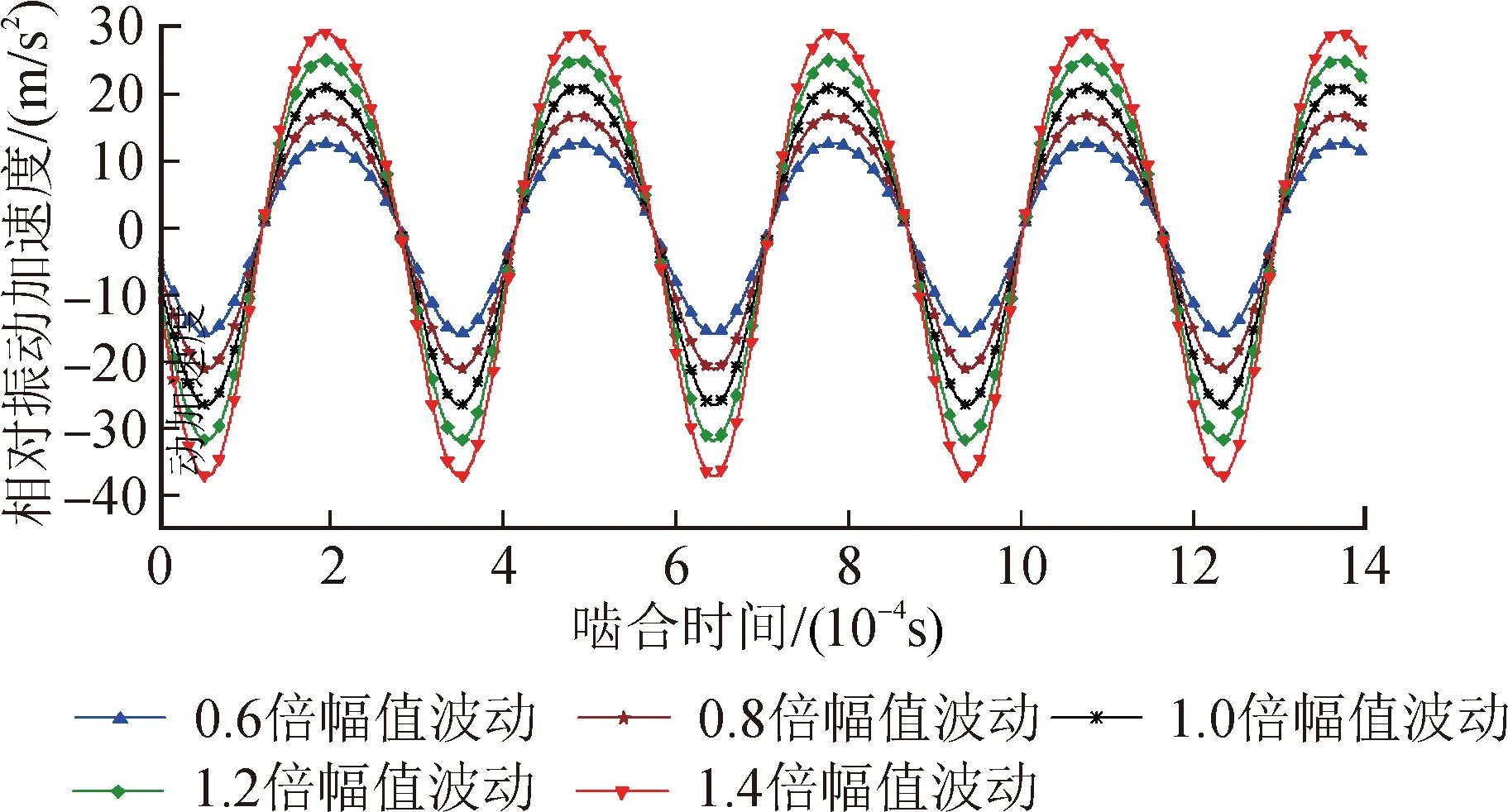
图14 12 000 r/min时不同幅值波动下啮合线方向振动时域图Fig.14 Time domain diagram of meshing direction vibration under different amplitudes of meshing stiffness at 12 000 r/min

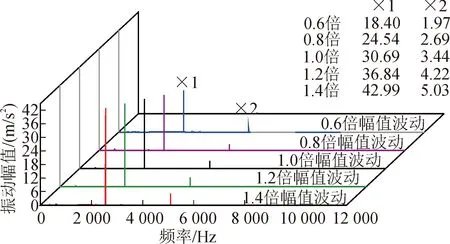
图15 9 000 r/min时不同幅值波动下啮合线方向振动频域图Fig.15 Frequency domain diagram of meshing direction vibration under different amplitudes of meshing stiffness at 9 000 r/min

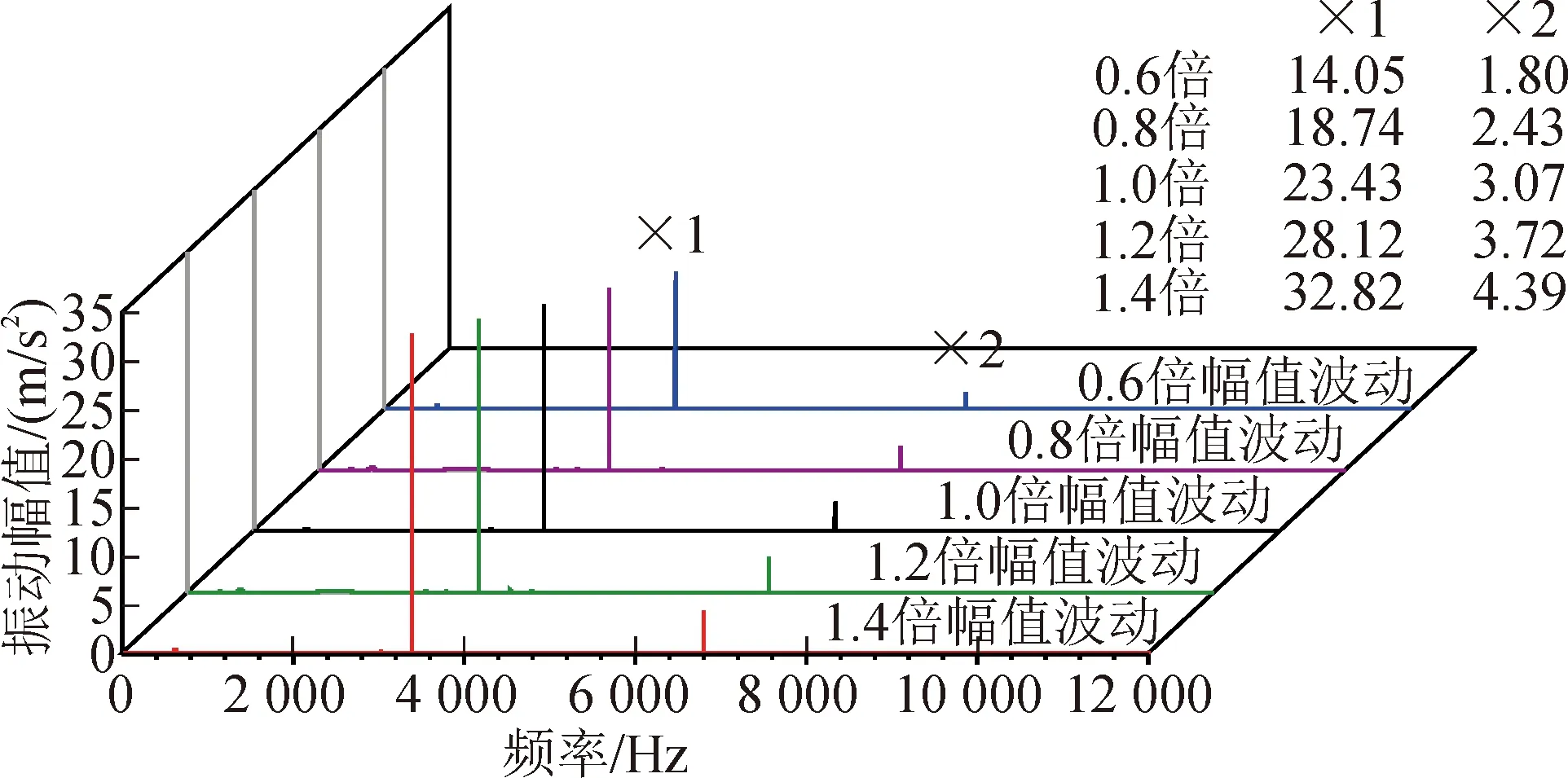
图16 12 000 r/min不同幅值波动下啮合线方向振动频域图Fig.16 Frequency domain diagram of meshing direction vibration under different amplitudes of meshing stiffness at 12 000 r/min

4 结 论

本文以某船用高速斜齿轮传动系统为研究对象，建立了考虑时变啮合刚度的斜齿轮弯-扭-轴耦合动力学模型，基于LTCA计算了齿轮副的时变啮合刚度，并研究了转速和齿轮副时变啮合刚度的变化对系统动力学特性的影响。所得结论如下。

1) 时变啮合刚度激励下，远离共振转速时，转速变化对系统振动特性的影响不显著。

2) 在1/3和1/2共振转速N0处，发生了明显的超谐波共振。

3) 齿轮副平均啮合刚度值增大会使系统振动幅值减小，但共振转速会发生改变，即系统固有频率会发生改变，齿轮平均啮合刚度越大，系统的共振转速也越大。

4) 时变啮合刚度波动幅值增大会使振动加剧，但不改变系统固有频率。