多年冻岩土区露天矿边坡局部稳定性探究

李国锋，李 宁,2，刘乃飞，朱才辉

(1. 西安理工大学 岩土工程研究所，陕西西安710048；2. 兰州交通大学土木工程学院，甘肃兰州730070； 3.西安建筑科技大学土木工程学院，陕西西安710055)

多年冻土和季节冻土区的面积约占地球陆地面积的50%，我国永久性冻土和季节性冻土的分布区域占国土面积的70%以上[1]。青海木里煤矿就处在青藏高原高寒带山地的多年冻土区，是青海省最大的煤炭资源分区之一。多年冻土区的露天矿边坡有其特殊的地层分布，本文对王晓东等[2]提出的地层概化模型进行优化，如图1所示。

图1 多年冻土区露天矿边坡的地层特性Fig.1 Strata status of open-pit slope in permafrost regions

永冻层上部为受温度影响的季冻层，边坡开挖后，坡表一定深度内的永冻层会变成季冻层，且永冻层下的不冻层在坡表处也会出现冻融交替现象。

该地区年最低气温-34 ℃，最高气温19.8 ℃，年平均气温为-4.2 ℃～-5.1 ℃，年平均地温-1.0 ℃～-3.5 ℃。由于气候的季节性冷暖变化，季冻层每年4月下旬开始融化，9月底至10月中旬达到最大融深，融化速度各月稍有差异，平均0.01 m/d，9月末气温开始下降，当进入负温后，季融层自上而下迅速回冻，至12月初季融层全部冻结。即在气温下降回冻开始或回冻后一段时间内会出现最大融化深度。张宝龙[3]、张宏刚等[4]经近 2 年多观测，认为该处季冻层厚约5～6 m，多年冻土层厚约58～60 m。徐拴海[5]进一步指出，季冻层在表层5 m 左右波动，并基于调查研究，首次提出了冻融岩土边坡5种基本破坏模式，指出逆层边坡多为中上部局部突出而下部崩塌，顺层边坡多为层间块片状脱落滑塌，切层边坡多为岩石劣化块体滑落或大块倾倒，破碎地层主要为表层剥蚀，而松散地层为掏蚀、滑塌等，并明确指出环境的反复剧烈变化主要影响坡体浅层地表，而其中温度变化是岩体性态改变的驱动力，水分是岩体冻融劣化的根源。

目前，关于多年冻土区的露天矿边坡稳定性分析评价方法，主要集中于强度折减法、极限平衡法及有效应力法。武鹤等[6]采用极限平衡法推导了寒区土质边坡冻融滑塌安全系数表达式，并讨论了各项参数对边坡稳定性的影响。曹兰柱等[7]，基于强度折减法探讨了不同开挖位置、开挖坡角和内排追踪距离下的边坡变形破坏机制和其对稳定性的影响规律。李荣建等[8]研究表明，传递系数法在分析边坡的局部滑动问题中具有明显的局限性。侯玲等[9]基于场变量的边坡有限元强度折减法实现了高效边坡安全系数求解，并基于最大等效塑性应变原理实现了边坡潜在滑动面位置的精细搜索。刘红军等[10]基于有效应力法推导了季节性冻土区边坡稳定性分析方法，且认为土质、地下水、气候、坡角、坡面朝向、冻结层是边坡失稳的主要影响因素。牛富俊等[11]指出，坡体表层土体变形和滑动可用有效应力分析法、总应力分析法、有效应力和固结理论等进行稳定性评价，认为地下冰水界面是热融滑塌型滑坡的滑面，且基于静力平衡法推导了安全系数表达式。

多年冻土区露天矿边坡具有其特殊的地层分布，在水冰相变、冻胀融缩的周期性影响下易产生局部滑塌或掏蚀破坏。强度折减法、极限平衡法等多为整体稳定性分析评价方法，不适用于局部损伤破坏演化分析与评价。因此，本文拟沿用笔者前文提出的“含相变三场耦合简化算法”和理想边坡模型[12,13]，探究边坡冻融局部损伤破坏演化过程，讨论基于屈服接近度的局部稳定性分析评价方法的实用性，并以此研究各因素对边坡稳定性的影响。

1 模型参数与方法

1.1 模型建立

木里煤田聚乎更矿区含F3、F7等断层及其它软弱结构面，但均埋藏较深，本文主要研究坡表局部的损伤破坏，故可忽略软弱夹层等的影响。因此，沿用如图2所示的理想边坡模型[13]，采用FLAC3D软件进行模拟分析。

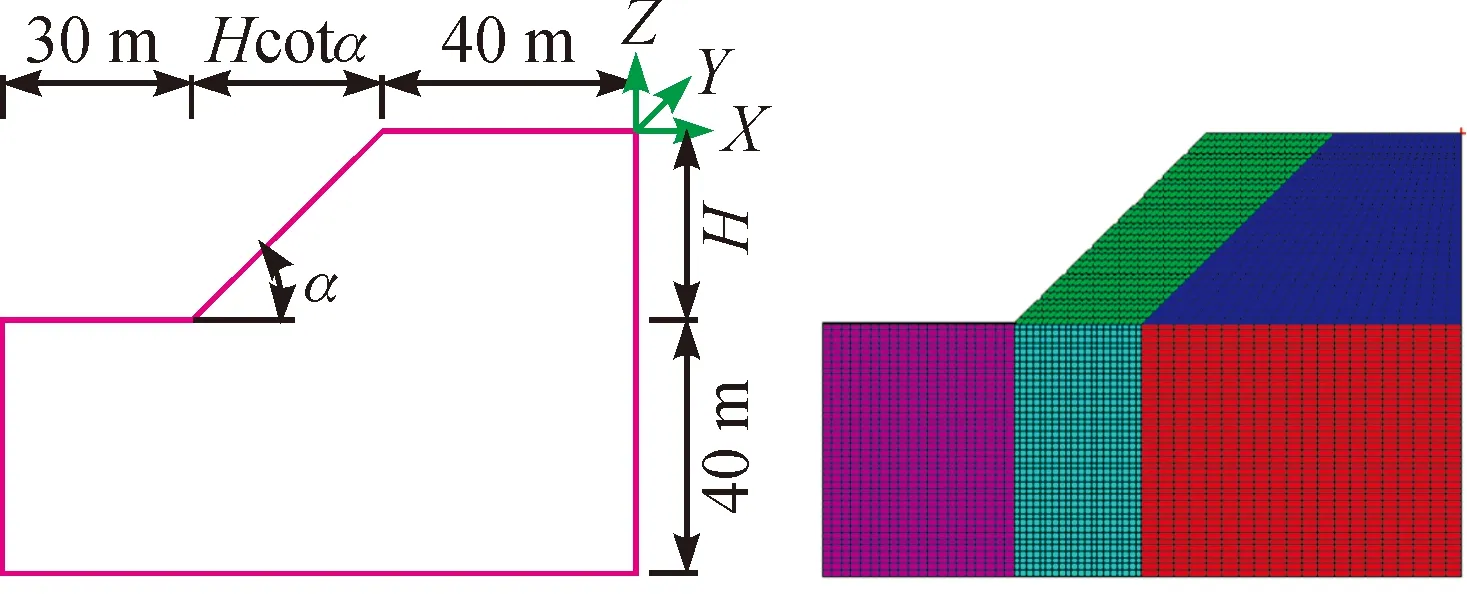
图2 计算模型Fig.2 Test model

其中，应力场、温度场及渗流场分别采用M-C模型、各向同性传导-对流模型、各向同性渗流模型。对模型底面进行全位移约束，侧面进行法向位移约束。该地区坡体稳定，主要是坡表季冻层受温度周期性的影响，而永冻层和不冻层相对比较稳定，基本不受大气温度影响，模型底面和侧面与大地基岩的热交换对坡表影响很小。为简化起见，假设模型侧面和底面与外界没有流体和温度交换，而坡表与外界有温度交换，则坡表采用透水对流温度边界，其余采用不透水绝热边界。由边坡岩土体自重产生初始应力场，并假设岩土体饱和。边坡初始温度T(h)按真实木里地温且按深度(h)分段施加，坡表温度T(d)按当地实际气温随时间天(d)变化：

(1)

T(d)=-7.1-26.9×cos(2π(d+110)/12.0/30.0)

(2)

1.2 参数选取

冻岩试样的相关试验不少[2,12-19]，但该处边坡涉及的是冻岩土体，其参数研究却不多，因此只能假设、简化或参见其它学者的研究成果。本文假设岩体参数随温度和冻融循环次数的变化规律近似同岩石试样，则只须对初始值乘以对应的折减系数即可。假设岩体热流场参数同岩石试样，仅考虑温度年冻融循环，而忽略温度昼夜循环的影响。边坡岩土体初始物理力学参数和热流场参数分别如表1～2所示。各参数的取值，在相关文献[12-13,16]中已进行了详细讨论。

表1 初始物理力学参数

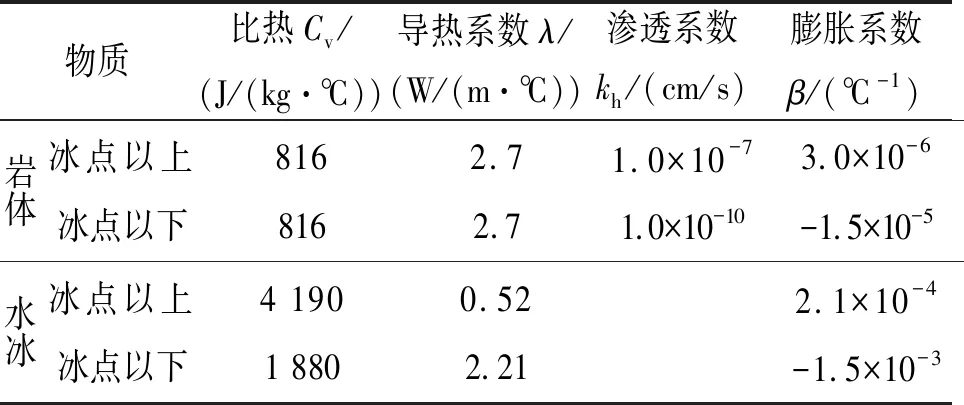
表2 热流学参数

冻融循环中岩石泊松比变化较小，可按初始值考虑[14]。假设只有变形模量和内黏聚力随温度和冻融循环次数[13]变化：

(3)

(4)

式中，T为温度；n为冻融循环次数；E(T)、C(T)分别为温度为T时对应的变形模量和粘聚力；KE、KC分别为冻融循环次数为n时对应的变形模量E和粘聚力C的冻融系数。

在整个冻融循环中，干燥岩样表现为热胀冷缩性，变形为弹性无残余变形，但饱水岩样经历了冷缩-冻胀-回温迟滞-融缩-热胀五个阶段，有明显的残余变形[15]。因此，对于饱水岩样，岩基依然遵守热胀冷缩规律，水分冻结体积增大使岩基孔隙扩大所产生的变形大于岩基自身冷缩变形，从而整体表现为冻胀；冰融化时体积变小，同时部分微裂隙闭合，从而整体表现为融缩；冰融化后岩基自身热胀变形和不可恢复的蓬松化变形组成了其残余变形。而对于冻岩土体工程而言，融化后水分散失，岩体强度也会降低，进而直观表象是融沉或者滑塌破坏。饱水岩样冰点上下分别表现“冷缩”和“冷胀”性质，且融缩后有残余变形[15]。因此，岩石基质热膨胀系数取3×10-6℃-1，水→冰相变时取-1.5×10-5℃-1，冰→水相变时可恢复热膨胀系数为-1.2×10-5℃-1[12,14]。水、冰在冰点以上取2.1×10-4℃-1，在冰点以下取-1.5×10-3℃-1。由于温度变化范围相对较小，故可认为岩石基质的比热和导热系数不变，且对静止空气的对流传热系数可取5 W/(m2·℃)。

1.3 含相变THM耦合简化算法

冻融循环下岩土体边坡稳定是一个复杂的动态平衡问题，具有显著的时效性，除了要考虑动态参数、边界外，还须要考虑水冰相变、多场耦合的作用。本文沿用作者前文[12,16]中的“含相变THM耦合简化算法”，对“热-流-力”进行顺次串联得到耦合算法。其核心是水冰相变前后单元温差对应的热量累计不小于相变潜热，只需采用FISH语言编写简单函数，将相变能量项用温差能量项代换即可。即在水→冰相变时，系统温度不变，释放的潜热抵消了系统在外界吸收热量下引起的温度降低；在冰→水相变时，系统温度不变，储存的潜热抵消了系统在外界释放热量下引起的温度升高。

1.4 屈服接近度分析方法

工程边坡稳定性分析主要研究坡体破坏范围、损伤破坏演化过程、变形破坏机理以及支护措施等，主要根据变形和应力判据来分析评价岩土体的安全状态。而多年冻土区露天矿边坡不同于一般边坡，其具有特殊的地层分布，在季冻层底是相当厚度的永冻层，两层之间则是富水的水冰临界薄弱面。融化部分岩体强度降低，在自重作用下主要发生浅表层局部块体或片状脱落、滑塌、崩塌等破坏，可采用极限平衡法近似求解其表层局部稳定系数，也可间接利用边坡局部经受冻融循环次数、局部变形量、局部损伤破坏体积等来评价，其中屈服接近度也是一种行之有效的方法。

周辉[19]提出屈服接近度(yield approach index，YAI)的概念，可广义地表述为：描述一点的现时状态与相对最安全状态的参量的比。屈服接近度YYAI∈[0,1]，数值越小，表示越接近破坏，当YYAI=0表示应力点达到破坏。高丽燕[20]对YAI重新进行定义，空间应力状态下一点的屈服接近度为：沿π平面坐标原点与应力点的连线方向，该点到屈服边界线的距离与π平面坐标原点到屈服边界线的距离之比，如图3所示。

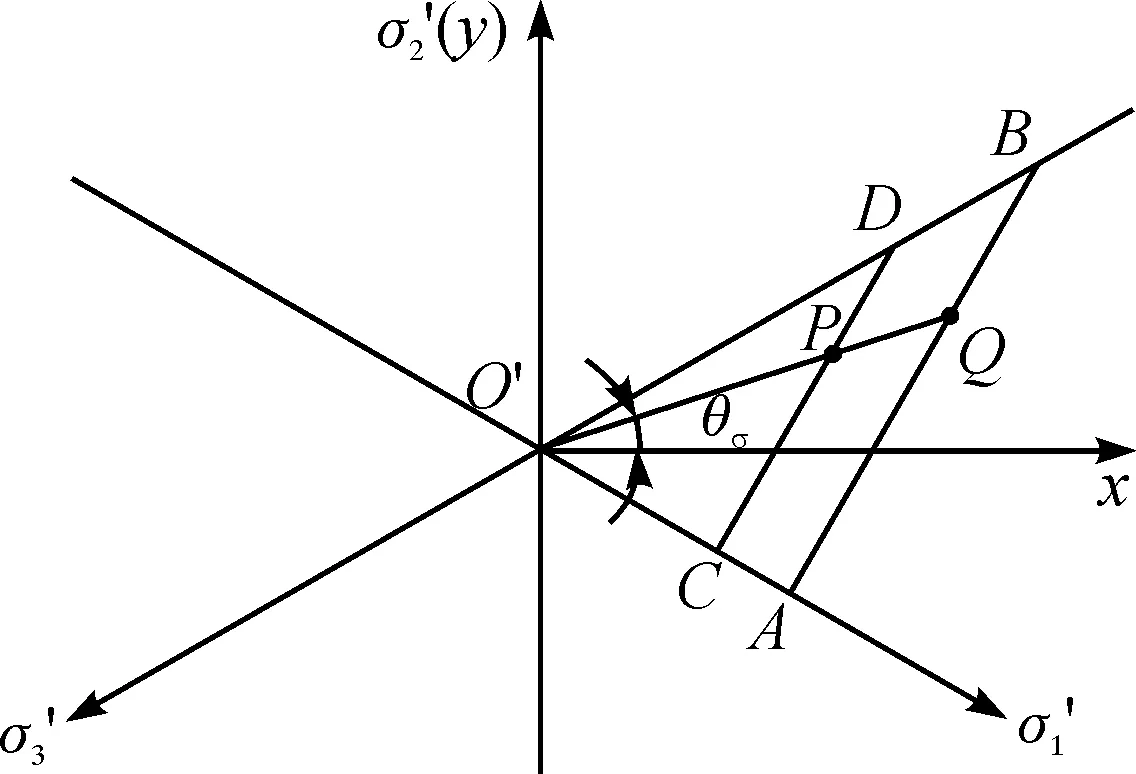
图3 屈服接近度π平面示意图Fig.3 YAI model on π plane

图3中，AB为屈服边界，Q点为O′P延长线与AB的交点，主应力空间的P点在π平面的坐标值可由这3个主应力计算得到。

对于M-C破坏准则，应力空间P点的屈服接近度可以表示为：

(5)

式中，σ1、σ2、σ3分别为P点第一、第二、第三主应力，上标′表示相应坐标轴名称；σt为抗拉强度；Ι1为第一主应力不变量；J2为第二偏应力不变量；θσ为应力洛德角；c为内粘聚力；φ为内摩擦角。

2 边坡稳定性分析

季节和昼夜交替产生的温差引起岩体中的水分反复相变冻融，而反复冻融又严重削弱岩土体的强度，严重威胁边坡的安全与稳定。多年冻土区露天矿边坡稳定性影响因素不同于一般的边坡，除了自身的形态尺寸外，主要还有温度、水分、冻融次数、应力状态等。因此，本节总结主要影响因素及其范围，设计如表3所示的试验方案，在基础方案基础上探究基于局部屈服接近度的稳定性分析评价方法的实用性及影响因素的敏感性。

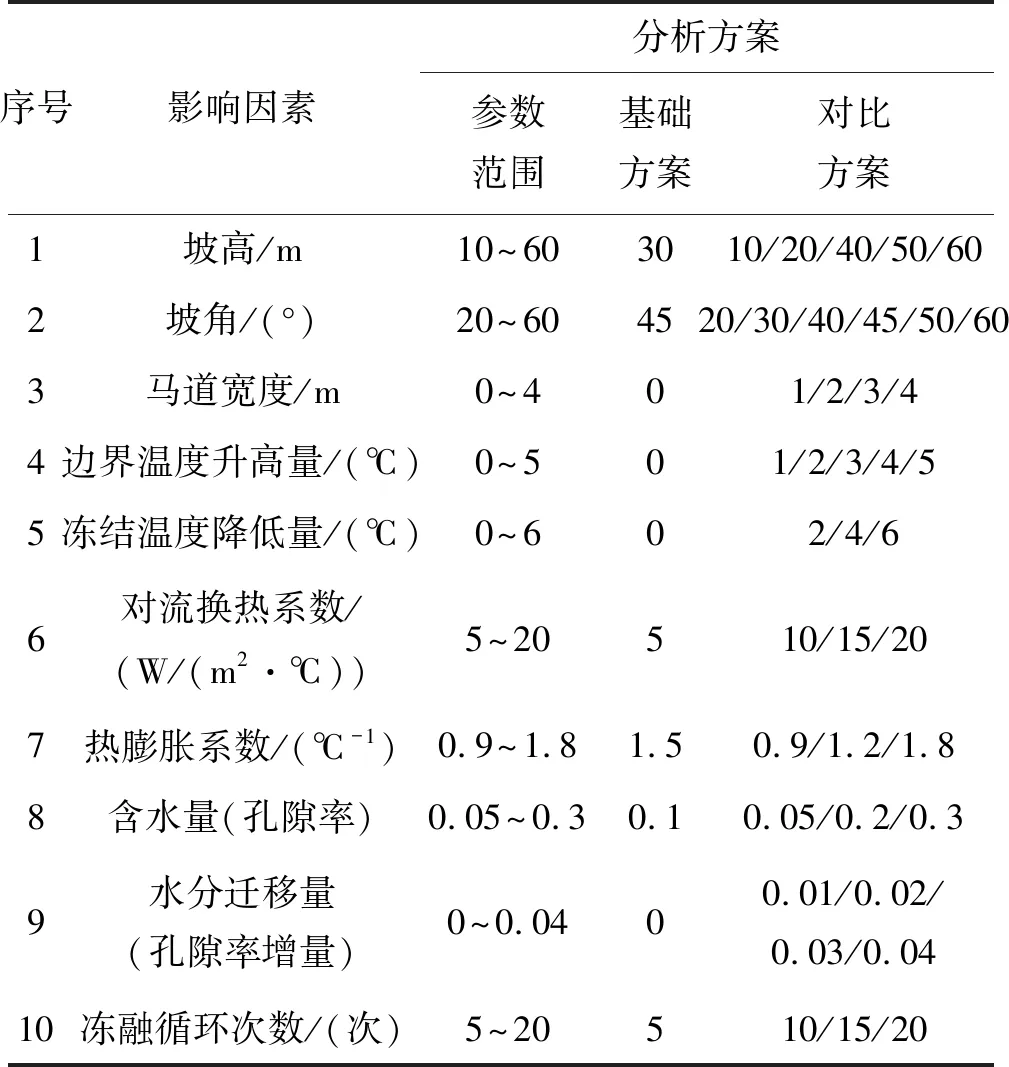
表3 冻融循环作用下边坡稳定性分析方案

其中，“边界温度升高量”和“冻结温度降低量”是预设的两个影响因素。全球变暖趋势早有定论，且联合国政府间气候变化专门委员会(IPCC)估计，21 世纪全球平均气温将增加1.4～5.8 ℃，而青藏高原未来50a气温可能上升2.2～2.6 ℃[21]。

2.1 冻融破坏演化过程

对基础方案的第5次冻融循环各月份的冻融深度、塑性区、拉应力区、剪应变增量区的演化过程进行分析，如图4所示，由于受篇幅所限，仅列出1、4、7、10月的相关结果。

由图4可知，3月底季冻层坡肩部位开始融化，7～9月达到最大融化深度约5～6 m，9月末气温下降进入负温，季融层自上而下迅速回冻，至12月初季融层全部冻结，冻融深度与实际调研情况十分相似。坡表1～4 m范围内主要存在拉剪塑性区历史，有发生滑塌破坏的趋势；坡表3～8 m范围内主要存在拉塑性区历史，可能由于水冰反复相变造成。回冻时由于冻胀力的作用，新拉塑性区会随着冻结面的回迁而内移，而在坡肩部位新生成拉剪塑性区。当季冻层融化时，由于表层热融滑塌的影响，会在坡肩、坡脚部位产生一定的拉应力。其中，8月拉应力区域最小，坡肩处拉应力不到0.05 MPa，而坡肩内一定深度却达0.21 MPa；当季融层回冻时，拉应力区会逐渐扩大并向永冻层深入，但最大值部位由坡内向坡肩处外移，其中12月拉应力最大为0.50 MPa，则可近似认为坡肩处岩体的最大冻胀力为0.45 MPa。变形区主要在坡肩呈“三角形”状分布，坡体浅层有沿季融层底冰面消融滑塌的趋势，与顶盖掏蚀现象类似，而坡肩内部是受力的关键，是坡体浅层安全的敏感区，如果在坡肩下部一定范围内进行加固，可在很大程度上提高坡体安全性。

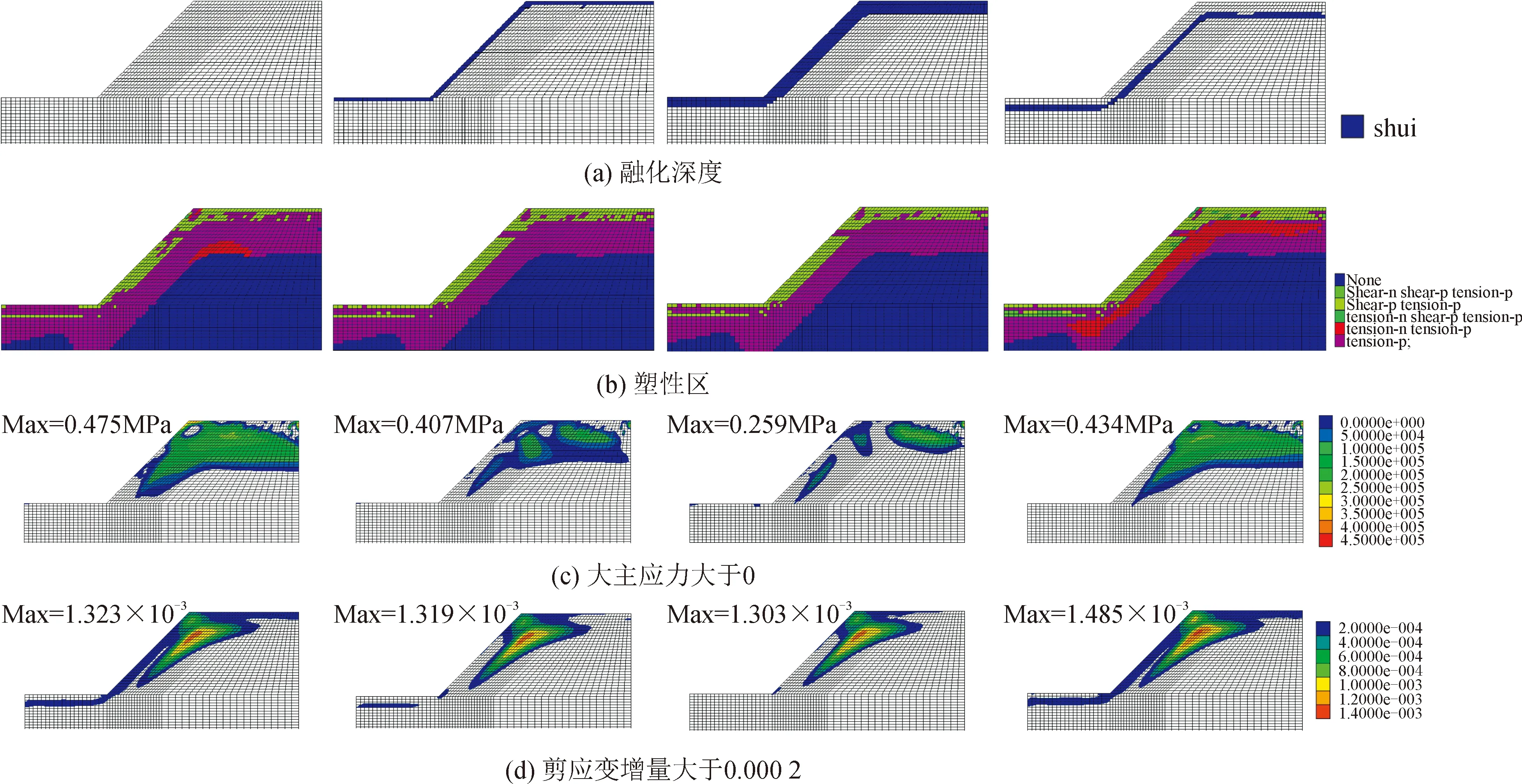
图4 冻融演化过程Fig.4 Evolution process on freezing-thawing

2.2 局部屈服接近度

将YYAI平均分成10段(0.0～0.1,…,0.9～1.0)，在整个计算模型中，每段内各单元的总体积占模型总体积的百分比即分段体积百分比，将分段百分比逐段累加即基于屈服接近度分段体积累计百分比。对基础方案的第5次冻融循环各月的屈服接近度分段的体积累计百分比进行分析，如图5所示。

由图5可知，各月份的屈服接近度分段体积累计百分比变化趋势基本一致，而在YYAI=0.6的邻域范围内或曲线的转折点附近各月份分布有所差异，其为易受水冰相变影响的区域，即冻融敏感区。且各月均在YYAI=0.8处增量最大，其中1月最小约为38%，而7月最大约为49%，其为坡体的内部稳定区。其中YYAI≤0.6的区域分布百分比约占整个模型体积的20%，基本属于受外界环境影响的冻融区或季冻层，即有效屈服区。同时，高丽燕[20]指出，YYAI≥0.2表示结构安全，那么可认为YYAI≤0.6为冻岩土边坡的损伤破坏的有效影响范围，而其中0.2

图5 屈服接近度分段的体积累计百分比Fig.5 Volume percentage on YAI distribution

虽然计算模型的边界范围取值对分段体积百分比有一定的影响，但对破坏损伤范围的分布基本不影响，同时模型网格越小，范围精度将越高。

YAI是空间应力状态下定义的，是在网格单元尺度上判断某一单元的损伤破坏程度，将同等级的YAI单元连接起来即YAI云图或等值线图。基础方案的第5次冻融循环各月份(1、4、7、10月)的有效屈服接近度云图，如图6所示。

由图6可知，有效屈服区YYAI≤0.6综合了拉剪破坏性质及其区域分布，整体呈三角形分布，且破坏区YYAI≤0.2集中于坡肩部位，而损伤区基本沿冻融面成层分布，且随着季融层的回冻在坡脚部位会产生屈服损伤区。

图6 各月YAI演化过程Fig.6 Evolution process on YAI

YYAI表示的是某一单元的屈服或破坏程度，对于冻融边坡工程的局部的安全程度而言，可采用边坡表层易受冻融影响有效屈服区(YYAI≤0.6)内各单元的屈服接近度的体积加权平均值来表示，即局部屈服接近度：

(6)

其中，Yi和Vi分别表示各区段单元的屈服接近度和对应体积，且YJB值越低，表明损伤破坏程度越严重。对第5次冻融循环内各月份的局部屈服接近度进行分析，如图7所示。

图7 局部屈服接近度历时曲线Fig.7 YJB changes with time

由图7可知，随着环境温度的升高，季冻层逐渐融化，3月局部屈服接近度快速下降，4月至7月达到最低，而后随着季融层回冻而升高。即每年4～7月份为危险月份，此时坡体浅层最可能发生局部崩塌或滑移破坏。因此，后续影响因素分析时，均以每年6月结果为基础进行对比分析。由此可见，基于“局部屈服接近度”的方法来分析边坡的局部安全稳定状态可行，对解决此类边坡问题有一定的参考意义。

2.3 影响因素的敏感性

为了方便后续影响因素分析，定义屈服相对比K，表示各对比方案的有效屈服范围内破坏或损伤范围分别与基础方案的有效屈服范围的比，K值越大，表明破坏或损伤程度相对越高。以第5次冻融循环6月的K值为例进行对比分析。

1) 影响因素整体分析

在基础方案基础上，在各影响因素变化范围内，进行单因素分析，当各因素分别平均增加10%时，对应的K平均增量百分比，如表4所示。

表4 K平均增量百分比

注：表中加粗数值表示各区段的3个较大值。

由表4可知，当各因素分别平均增加10%时，冻结温度对局部屈服区域影响最大，达到10.23%，而其中大部分主要影响的是损伤区，即永冻层上缘区域，那么在实际工程中应防止因人为因素而导致的冻结温度降低。坡高和冻融循环次数对局部屈服区影响次之，且其依然主要影响的是损伤区，而坡角和热膨胀系数直接导致坡体发生破坏。在参数变化范围内，对局部有效屈服区的影响程度从大到小依次是：冻结温度、坡高、冻融循环次数、热膨胀系数、孔隙率，而其中对局部破坏区的影响程度从大到小依次是：坡角、热膨胀系数、坡高、孔隙率、冻融循环次数。

2) 单因素影响分析

由上节可知，坡高、坡角、冻结温度降低量、热膨胀系数、孔隙率、冻融循环次数等对边坡局部安全性影响较大，因此，本节对这些因素进行详细分析，如图8所示。

由图8(a)、(b)可知，多年冻土深度范围内，随着坡高的增加，有效屈服区和损伤区逐渐增大，而已破坏和临近破坏区先增加到40 m处达到极值而后逐渐降低。其中，坡高每增加10 m，已破坏、临近破坏和损伤区比例分别增加0.009、0.017、0.093，说明坡高的增加容易导致坡体内部的损伤积累。随着坡角的增加，有效屈服区变化不大，而损伤区逐渐减小，已破坏和临近破坏区整体呈增大趋势，而临近破坏区先增加到50°处达到极值而后有降低趋势。其中，坡角每增加10°，已破坏、临近破坏和损伤区比例分别增加0.057、0.030、-0.093，说明坡角的增加容易导致坡体表层的破坏。

由图8(c)、(d)可知，随着冻结温度的降低，有效屈服区和损伤区逐渐增大，而已破坏和临近破坏区域变化不大。其中，冻结温度每降低2℃，已破坏、临近破坏和损伤区比例分别增加-0.001、0.010、0.332，说明冻结温度的降低容易引起坡体内部的损伤积累。随着热膨胀系数的增加，各屈服区域均增加，其中热膨胀系数每增加0.3 ℃-1，已破坏、临近破坏和损伤区比例分别增加0.041、0.037、0.045，说明热膨胀系数的增加将整体增大坡体的破坏与损伤区域。

由图8(e)、(f)可知，随着孔隙率的增大，有效屈服区、损伤区和已破坏区先增加到0.2处达到极值而后逐渐降低。其中，在极值前孔隙率每增加0.05，已破坏、临近破坏和损伤区比例分别增加0.050、0.026、0.043，说明孔隙率的增加将整体增大坡体的破坏与损伤区域。随着冻融循环次数的增加，各屈服区域均呈增加趋势但增率变缓，且早期主要影响的是已破坏区域而后期主要影响损伤区域。其中，冻融次数每增加5次，已破坏、临近破坏和损伤区比例分别增加0.011、0.014、0.136，说明冻融次数的增加主要引起损伤区的累积。

3 结 论

本文沿用 “含相变三场耦合”简化算法和理想边坡模型，探究了边坡冻融局部损伤破坏演化过程，讨论了基于屈服接近度局部稳定性分析方法的实用性，并以此探究了各因素对边坡稳定性的影响。

1) 模拟的冻融深度与实际调研情况十分相似，新拉塑性区会随着季融层回冻而内移，而拉应力最大值区域反而外移至坡肩。变形区主要在坡肩呈“三角形”状分布，有产生消融滑塌的趋势，与顶盖掏蚀现象类似。坡体浅层有沿季融层底冰面滑塌的趋势，而坡肩内部是坡体整体安全的受力关键。

2) 冻岩土体边坡的局部有效屈服区为YYAI≤0.6，而其中0.2

3) 各影响因素对局部有效屈服区的影响程度从大到小依次是：冻结温度、坡高、冻融循环次数、热膨胀系数、孔隙率，且坡高、坡角、孔隙率分别存在40 m、50°和 0.2的极值。坡高的增加、冻结温度的降低、冻融次数的增加主要导致坡体内部的损伤积累，坡角的增大更易导致坡体表层的破坏，而热膨胀系数的增加、孔隙率的增加将整体增大坡体的破坏与损伤区域。