一元二次方程的解法(二)配方法
2019-05-28湖北省麻城市福田河中心学校吕延涛
湖北省麻城市福田河中心学校 吕延涛
配方法作为一元二次方程的解答方式的一种,在培养学生的解题能力,强化学生的素质发展方面发挥着至关重要的作用。因此,为了加强数学教学的效率和效果,教师就要从教学内容和学生的实际状况出发,为学生构建多样化的数学活动。本文结合笔者的实践经验,对于如何讲解“一元二次方程的解法(二)配方法”进行了以下几点探究:
1.创设情境,引入配方法
有效的数学情境,不仅能够激发学生的兴趣,还能够促进学生的思维发展。并且,情境教学是最符合初中生的性格特点的教学手段之一。因此,教师在讲解一元二次方程的解法的过程中,就可以联系学生已经掌握的知识,为学生构建数学情境,从而加深学生的印象,使学生能够从根本上理解配方法,同时这也是引出配方法的重要渠道之一。
比如:笔者曾经为学生提出了这样一个例题:x2+8x+6=5。首先笔者提出了问题:你能够解出这个一元二次方程吗?有的学生就提到了用直接开平方的方式就能够解答出来。紧接着,笔者又提出了问题:那么你能够解出x2+8x+1=0 吗?学生在经过思考和分析之后,就发现,两边的方程都减去5 就变成了x2+8x+1=0,这是我们刚刚才解决过的问题。然后,笔者根据学生的思路,为学生分析了解答的过程:方程x2+8x+6=5 两边同时减去5,就变成了x2+8x+1=0,这是对等式基本性质的应用。最后,笔者就根据这道题的解题思路,引出了配方法,首先,笔者引导学生将常数项移到了等号的右边,也就是x2+8x=-1,然后再将等式两边同时加上一次项系数一半的平方16,就能够得到x2+8x+16=15,(x+4)2=15,所以学生在这样的解题情境中,就能够掌握配方法的解决思路。
2.提出问题,理解配方法
问题是数学教学的灵魂。科学合理的问题,不仅能够吸引学生的注意力,培养学生的探究能力,还能够加强学生的实践能力。学生只有在解题的过程中,才能够充分地理解配方法的运用规律。因此,教师就要及时提出问题,从而加深学生对配方法的理解和认知。
比如:在经过情境的创建之后,学生对配方法已经有了一个基础的了解。因此,为了加深学生对配方法的理解,笔者就为学生提供了例题:3x2+8x-3=0。并且,笔者根据这个题目,规范了学生的解题步骤:化1,移项,配方,变形,开方、求解,定解。学生在笔者的引导下,就能够掌握解题的正确方法。可见,要想让学生理解和掌握配方法,就必须要在实际的题目中为学生讲解相关的知识。只有这样才能够取得良好的教学效果。
3.加强练习,应用配方法
练习是巩固学生知识的重要手段之一。并且,学生只有做过大量的题目之后,才能够构建起解决问题的模型。因此,教师就要注重课后练习活动的组织,从而提高学生的应用能力。

4.中考链接,深化配方法
在初中数学教学中,最重要的就是要培养学生的解题能力。而中考就是对学生数学能力的终极考验。因此,要想使学生拥有面对中考的能力,教师就要结合中考真题,为学生讲解配方法的应用策略。只有这样,学生才能够深化学生对配方法的理解。
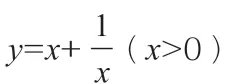
总之,教师在日常教学的过程中,一定要注重学生的主观体验,并且,教师要从学生的兴趣和学习状况出发,为学生构建多样化的数学课堂,从而满足学生的情感体验,强化学生的综合素养。
