高超声速导弹流场与结构温度场耦合数值分析*
2019-05-28徐世南吴催生
徐世南,吴催生
(中国空空导弹研究院,河南洛阳 471000)
0 引言
目前世界各国都大力投入高超声速导弹的研制,试图抢占高超声速实战化先机,以其为应用背景的验证项目相继进行。但也面临试验要求技术难度大、经费高等困难。采用计算机仿真对高超声速导弹进行流场、结构温度等准确预测,可以对其热防护与结构设计提供指导[1-3]。
对于高超声速飞行器热、力等载荷环境的数值模拟,传统方法忽略耦合效应的影响,即未考虑结构变形与温度、压力之间的耦合关系。仲继泽等[4]发展了一种基于流-固单向耦合的方法,得到了机翼的力载荷。韩玉琪等[5]通过定常流动换热分析计算飞行器涡轮盘的热、力载荷,传递给盘体得到其应力场。此方法虽然计算效率高,但当耦合效应明显时,无法精确预示热力学环境。随着仿真技术的发展,考虑耦合效应影响的求解方法得到了广泛开展,保证计算结果更加精确。周印佳等[6]采用分区求解方法,将计算区域分为流体区域和固体区域,在耦合交界面进行数据传输,完成了高超声速流动与结构的耦合分析。由于此方法耦合子物理场在一个时间步内只进行一次数据交换,时间精度上仅能达到一阶,安效民等[7]在流固之间引入内迭代,使分区耦合方法在时间方向上达到了二阶时间精度。肖军等[8-9]将气动和结构动力方程各自构造子迭代求解,也获得了每一物理时间步的高精度结果。黄唐等[10]建立和流固之间的联系,实现了流场、热、结构一体化数值模拟。
高超声速导弹处于一个复杂的多场耦合环境,采用合适的计算方法对其进行仿真分析,能够更有效的得到导弹热/力载荷。文中基于分区耦合方法,建立高超声速导弹平飞状态的仿真模型,对其流场和结构温度场进行仿真分析,并研究温度场、压力场和结构变形之间的关系。
1 控制方程和耦合策略
1.1 控制方程
在进行流-固-热耦合计算时,各自域内遵循基本的守恒原则,其中流体控制方程采用积分形式的N-S方程[11]:
(1)
式中:Q为守恒变量;G为无黏通量;GV为粘性通量;t为物理时间;∂Ω为某一固定区域Ω的边界;dS为面积微元;n为控制边界法向单位矢量。
对式(1)按有限体积法进行空间离散可得:
(2)
式中:VI为第I个控制体单元;NF为包围第I个单元的所有面数;ΔSm为第m个表面的法向量。
由于结构温度与变形存在相互耦合关系,利用有限单元法对其进行统一求解。基于静气动弹性,将变分原理应用于热传导控制方程、结构控制方程以及它们相应的边界条件,可得到如下形式的热-结构有限元矩阵方程:
(3)
式中:K为结构刚度矩阵;KT为热传导矩阵;KuT为热弹性刚度矩阵;u为位移向量;T为温度向量;F为力载荷向量;QT为热载荷向量。
1.2 耦合策略
采用分区求解方法,将计算区域分为流体区域和固体区域。在流体区域内求解统一的流体控制方程得到热流qf和压力pf,并将其通过耦合界面传递给固体区域;在固体区域内,求解热-结构控制方程得到结构壁面温度Ts和位移us,并将其通过耦合界面传递给流体区域。基于ADINA软件,完成对高超声速导弹气动/热/结构的多场耦合分析,具体实现形式如图1所示。
1)将初始设置的结构壁面温度Ts和结构位移us作为仿真分析初始条件通过耦合界面传递给流体区域;
2)在流体区域进行气动热力学仿真计算,得到热流qf和壁面压力pf;
3)热流qf和流体壁面压力pf通过耦合界面传递给固体区域;
4)在固体区域进行热-结构仿真计算,得到结构壁面温度Ts和结构位移us;
5)对流体区域和固体区域计算结果进行收敛检查,检查流体压力pf和结构温度Ts是否满足收敛标准,如果不收敛,继续在t0时间步进行迭代计算,直到满足收敛标准或达到设置的迭代次数,如果满足收敛结果,输出此时间步计算结果并进入t0+Δt时间步的迭代计算;
6)不断循环该过程,直至设置的时间终止值,完成多场耦合数值计算。
2 仿真校验
为验证耦合计算方法有效性,以经典圆管绕流实验作为算例[12]。实验来流参数见图2,圆管内半径25.4 mm,外半径38.1 mm。圆管材料为不锈钢,材料热力学参数可参见文献[12-14]。圆管内壁设为等温壁,温度值为294.4 K。图3为计算初始时圆管表面压力与文献[12]实验结果对比,图中p0为驻点压强,θ为物面到圆心的连线与x轴的夹角。图4为计算的驻点2 s的温度变化,仿真值与文献结果相符。验证了耦合仿真方法的有效性。
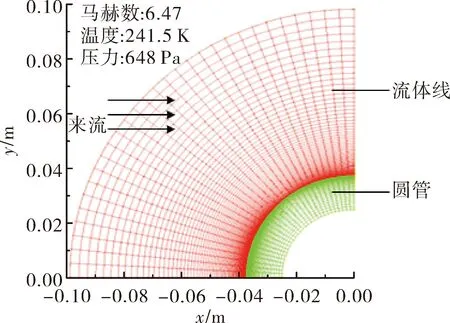
图2 二维计算网格
3 计算结果分析
3.1 仿真模型
采用某无翼/舵布局高超声速导弹,不考虑内部元器件与辐射效应;导弹头部为陶瓷材料,弹身为钛合金材料,具体材料参数见表1。导弹仿真模型如图5所示,长细比L/D为20,L为导弹全长,D为导弹弹径。仿真边界条件设置为:在AB、BC、CD边界施加速度、压力和温度载荷;导弹结构为固体场,外场和内场为流体场,流体场与固体场交界面为耦合界面。仿真参数为:来流压力、温度、速度分别为7 494 Pa、216.5 K、5Ma,攻角为0°,初始温度293 K,初始压力7 494 Pa。采用瞬态计算,并基于仿真终止时间40 s进行研究。
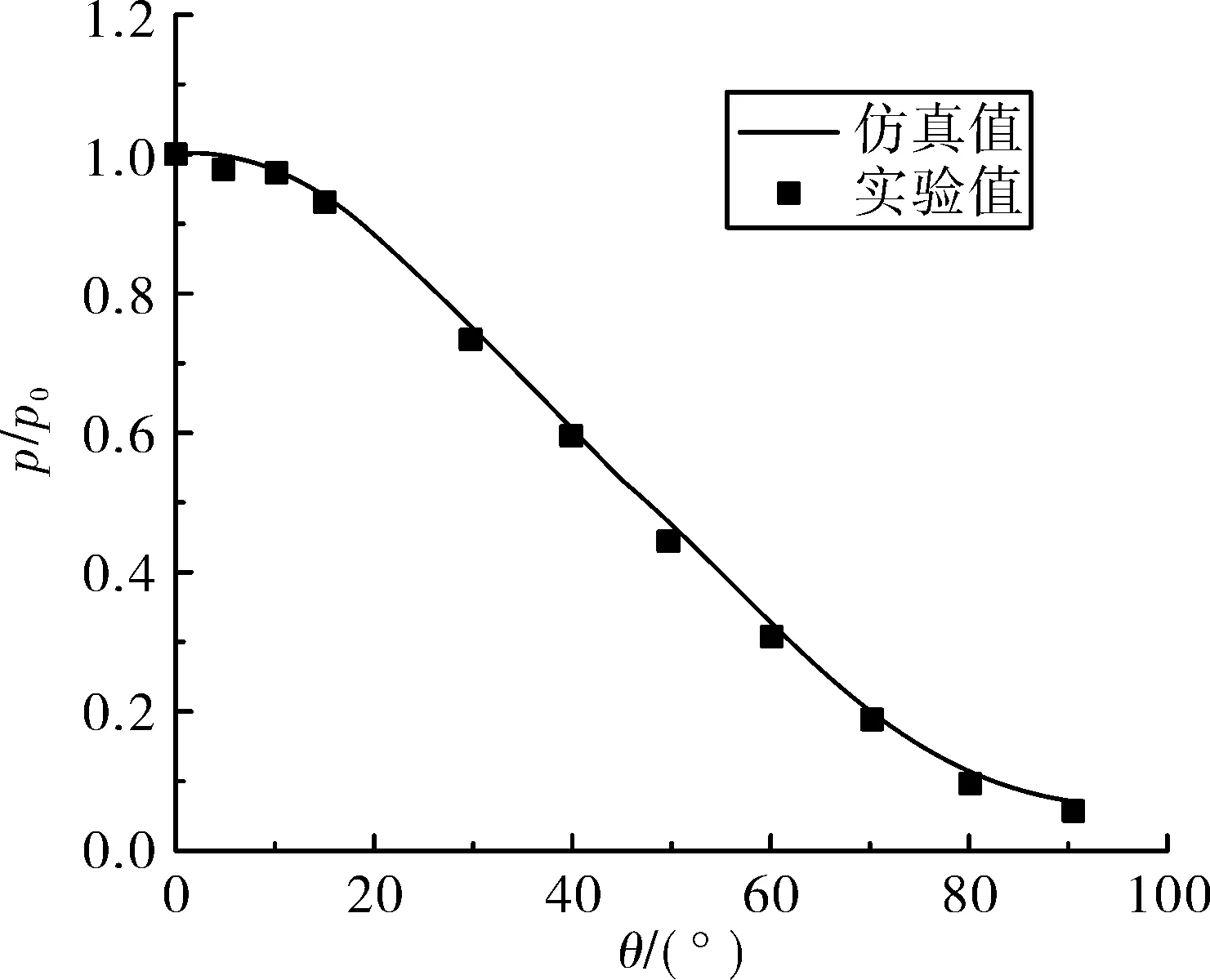
图3 壁面归一化压力分布与实验结果对比
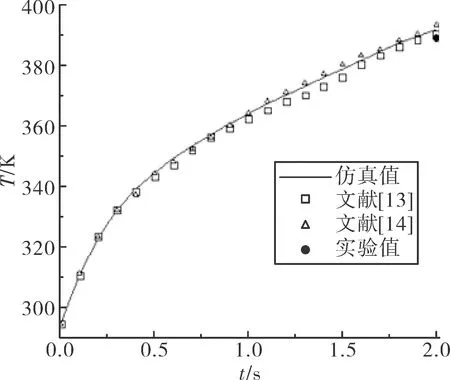
图4 驻点温度随时间变化
由于温度场、压力场与结构变形之间存在耦合效应,将影响因素分为以下3种:
1)热因素,即仿真计算时结构变形仅由热变形造成;
2)气动力因素,即仿真计算时结构变形仅由气动力造成;
3)无变形因素,即仿真计算时结构无变形。
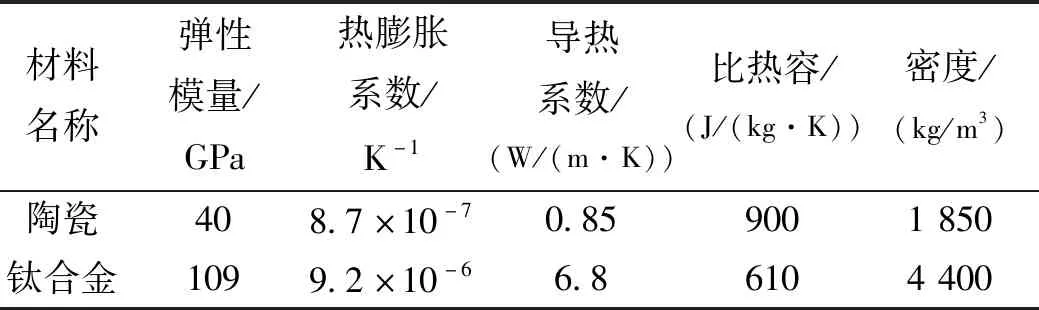
表1 材料参数
3.2 结构变形分析
研究结构变形,定义轴向变形量为ΔL/L×100%,式中ΔL(假设拉伸为正值,压缩为负值)为结构沿X轴方向的位移量;定义径向变形量为ΔD/D×100%,式中ΔD(假设膨胀为正值,收缩为负值)为结构沿Y轴方向的位移量。横坐标进行归一化处理,坐标数值为:x/L,导弹头部最前端位置为坐标原点,x表示导弹轴向位置,L为导弹全长。其变形量如图6所示,结构沿X轴发生轴向拉伸,沿Y轴发生径向膨胀。
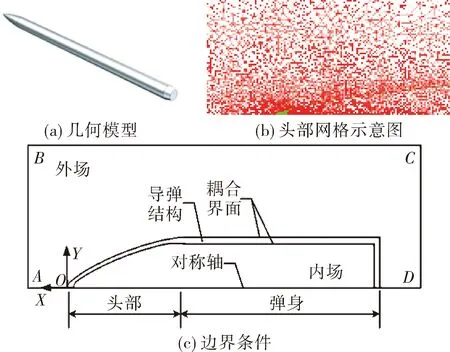
图5 仿真模型
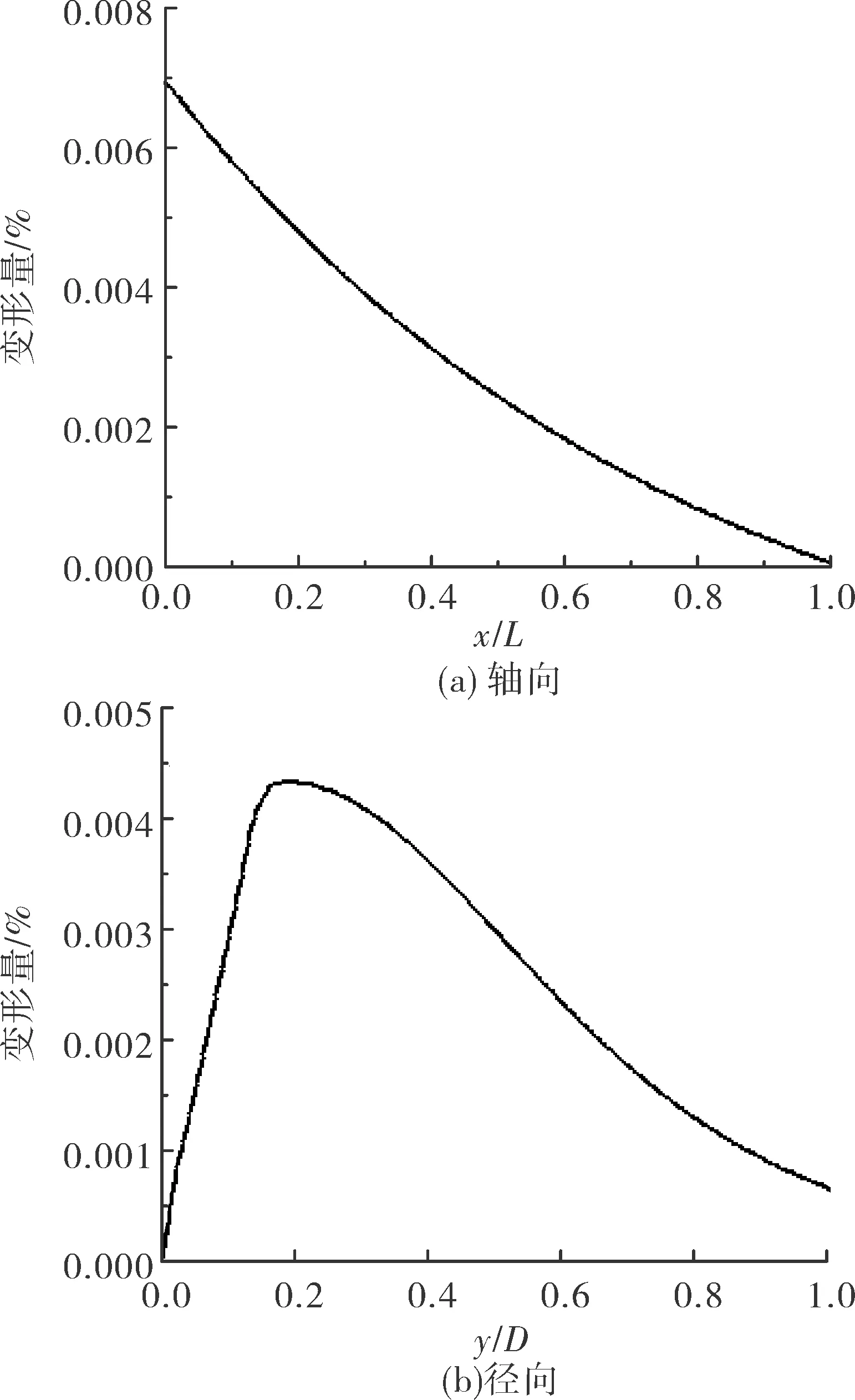
图6 结构变形图
以头部末端位置为例,研究气动热和气动力对结构变形的影响,如图7所示,在导弹平飞状态,热因素使结构发生拉伸和膨胀,气动力因素与之相反,其中结构变形主要由热因素引起。
3.3 温度与压力分析
导弹外壁温度与压力分布如图8所示,头部温度与压力载荷值大,越靠近头部位置,来流发生的摩擦和压缩越剧烈,动能转化成的热能越多,速度的变化梯度也越大。
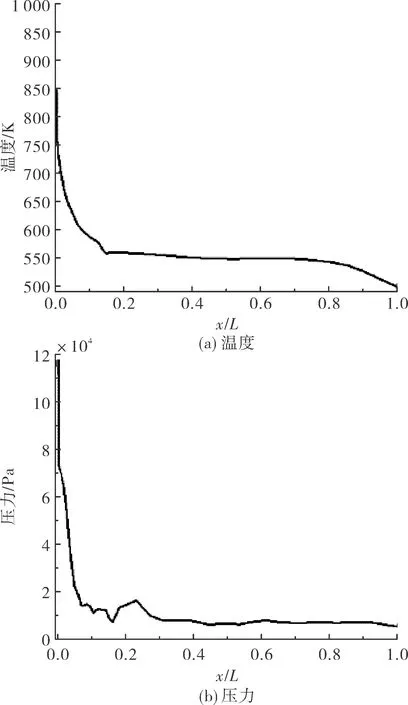
图8 温度与压力曲线
以头部末端位置为例,研究耦合效应对温度和压力的影响,如图9所示,在导弹平飞状态,耦合效应对温度和压力的影响较小,结构变形量不大,不足以改变流场与结构温度场分布。
3.4 耦合算法适用性分析
虽然考虑耦合效应,采用双向耦合算法仿真结果更精确,但是计算效率比不考虑耦合效应的低,在实际应用中,仿真值在许用误差范围内即可。通过改变弹身长度研究不同长细比下耦合效应对导弹气动热、气动力载荷的影响。以头部末端位置为例,如图10所示,图中ΔT、ΔP分别为考虑耦合效应与不考虑耦合效应的温度差和压力差,P为考虑耦合效应的压力值。由图10可知,导弹在不同长细比下,耦合效应对仿真计算结果影响均较小,实际分析时可忽略耦合效应以提高计算效率。
4 结论
基于高超声速导弹平飞状态分析得到以下结论:
1) 导弹弹体结构发生轴向拉伸和径向膨胀,且气动加热对结构变形影响较大。
2) 头部位置气动热与气动力环境较为严酷。
3) 结构变形对压力和温度仿真影响结果较小。
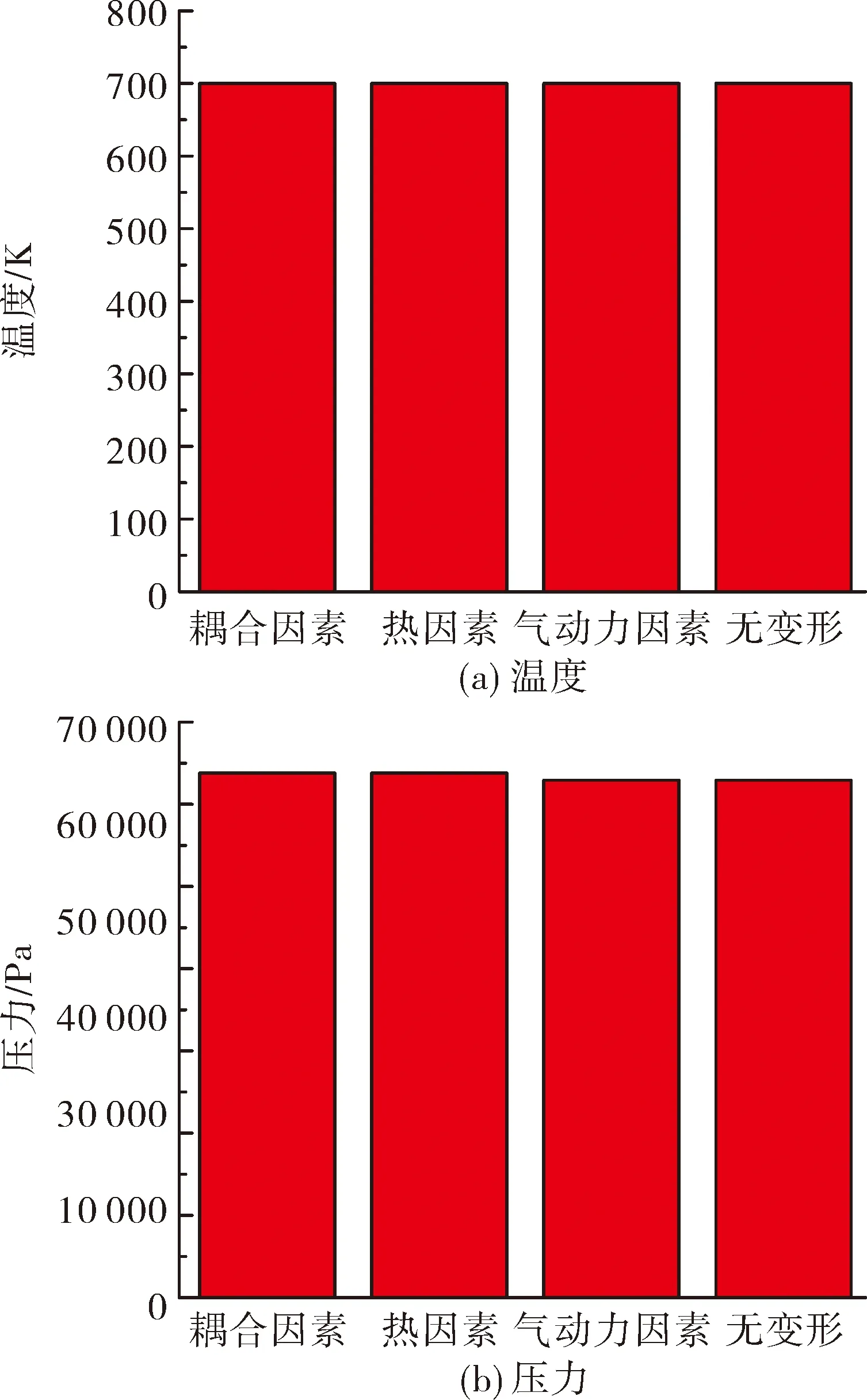
图9 耦合效应对温度与压力影响
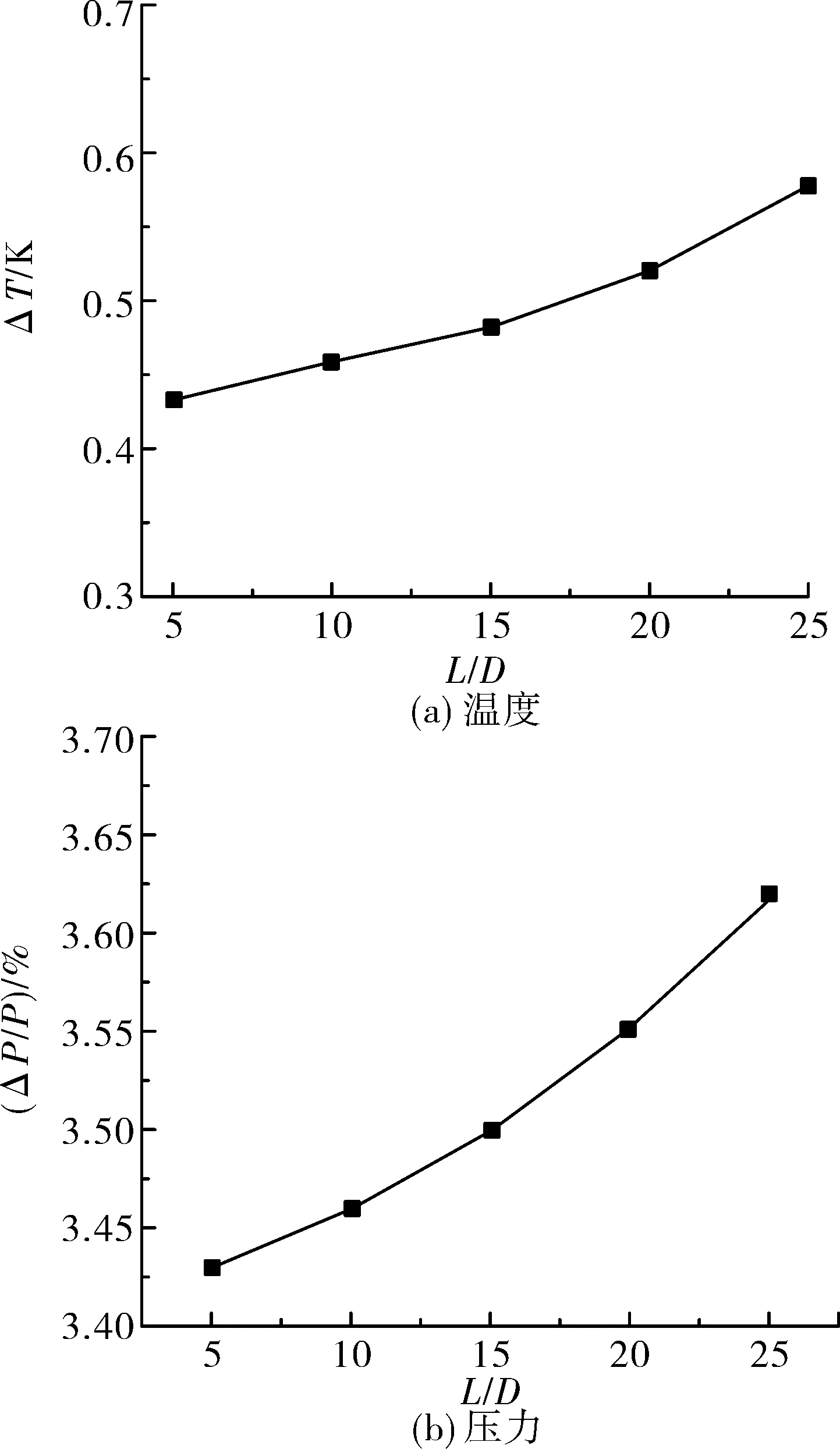
图10 不同长细比仿真值对比
4) 对导弹进行气动热和气动力分析时,可不考虑耦合效应以提高仿真计算效率。
