大型导弹起竖机构三铰点配置优化技术研究*

孟利军，郭云鹤，凡永华

(1 西京学院，西安 710123；2 上海机电工程研究所，上海 201109；3 西北工业大学，西安 710072)

0 引言

陆基机动导弹发射装置中的导弹起竖是一个变负载的运动过程，在起竖初始阶段负载转矩较大，随着导弹起竖角度增加，负载转矩随之减小；其驱动缸的推力和行程随着三铰点布局不同而改变[1-2]。以往文献对起竖装置的机械结构、动力驱动方式以及控制理论研究较多，但对三铰点的布局配置研究较少[3-6]。文中以某型导弹发射车为例，建立了三铰点式、二级缸驱动起竖机构的数学模型，通过分析改变铰点之间的位置关系对起竖过程的力学和起竖时间的影响，给出了三铰点的优化图表，研究结果可为导弹起竖机构的优化设计提供参考。

1 起竖机构数学模型的建立

图1为某型导弹发射装置的示意图。导弹装填在发射筒内，发射筒置于发射车上，借助铰链与发射车尾部及起竖缸的两端鱼耳相连，发射筒绕O点旋转至垂直位置，使导弹处于待发状态。

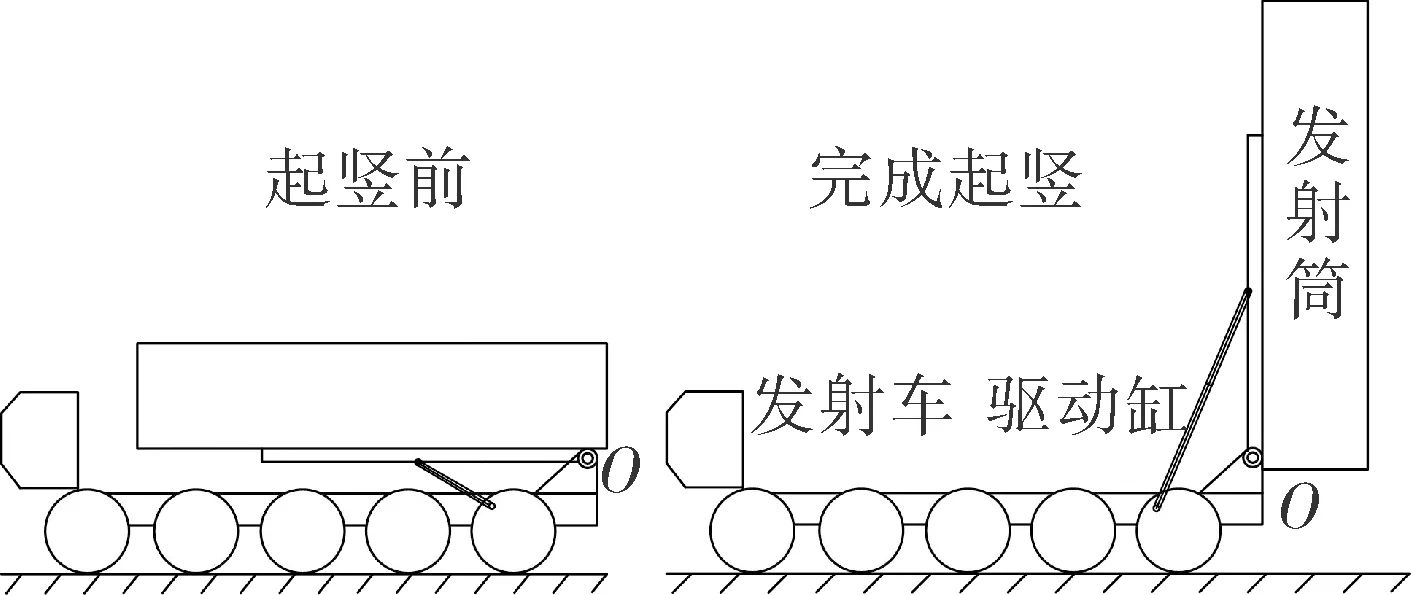
图1 某型导弹发射装置示意图

起竖机构的运动简图如图2所示，由3个转动副和一个移动副组成。由机械原理可知，该机构的自由度为1，故在驱动缸的推力作用下，发射筒将获得确定的运动规律。

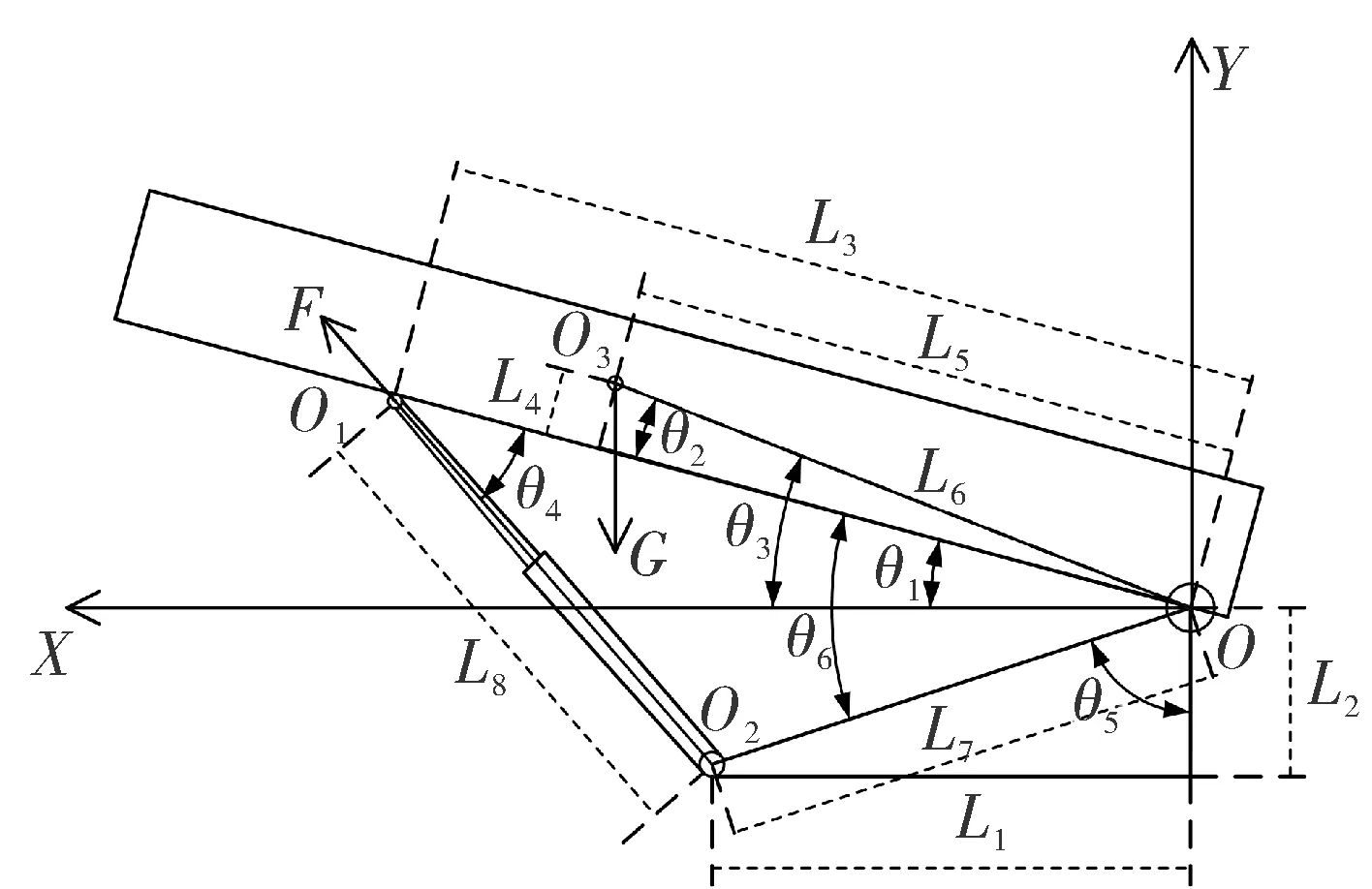
图2 起竖机构运动简图

发射车的主要参数如下：

1)质心O3沿垂直于导弹方向距旋转支点O的距离L4=1.500 m；

2)质心O3沿导弹方向距旋转支点O的距离L5=5.790 m；

3)质量m=60 000 kg；

4)重力加速度取g=9.8 m/s2；

5)旋转支点O到缸下支点O2的水平距离为L1；

6)旋转支点O到缸上支点O1沿导弹方向的距离为L3；

7)L1和L3为可变量，取值范围均为2～11 m。

2 驱动缸的受力分析

首先分析不同三绞点配置下驱动缸的受力情况。选取发射筒和导弹为研究对象，对O点建立力矩平衡方程，作用于研究对象的主动力矩为发射筒、导弹的重力矩和驱动缸的推力矩，约束反力力矩为0，列写以下方程：

(1)

(2)

(3)

(4)

θ3=θ1+θ2

(5)

(6)

(7)

(8)

(9)

利用MATLAB求解方程组，并绘制当角度不同时，L1和L3变化时，对应缸的受力F的三维图。

1)当角度为0°时，L1和L3变化时对应缸的受力F0的三维图如图3所示。

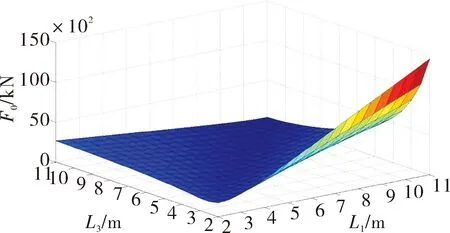
图3 初始位置受力

2)当角度为30°时，L1和L3变化时对应缸的受力F30的三维图如图4所示。

图4 起竖30°时的受力

3)当角度为60°时，L1和L3变化时对应缸的受力F60的三维图如图5所示。

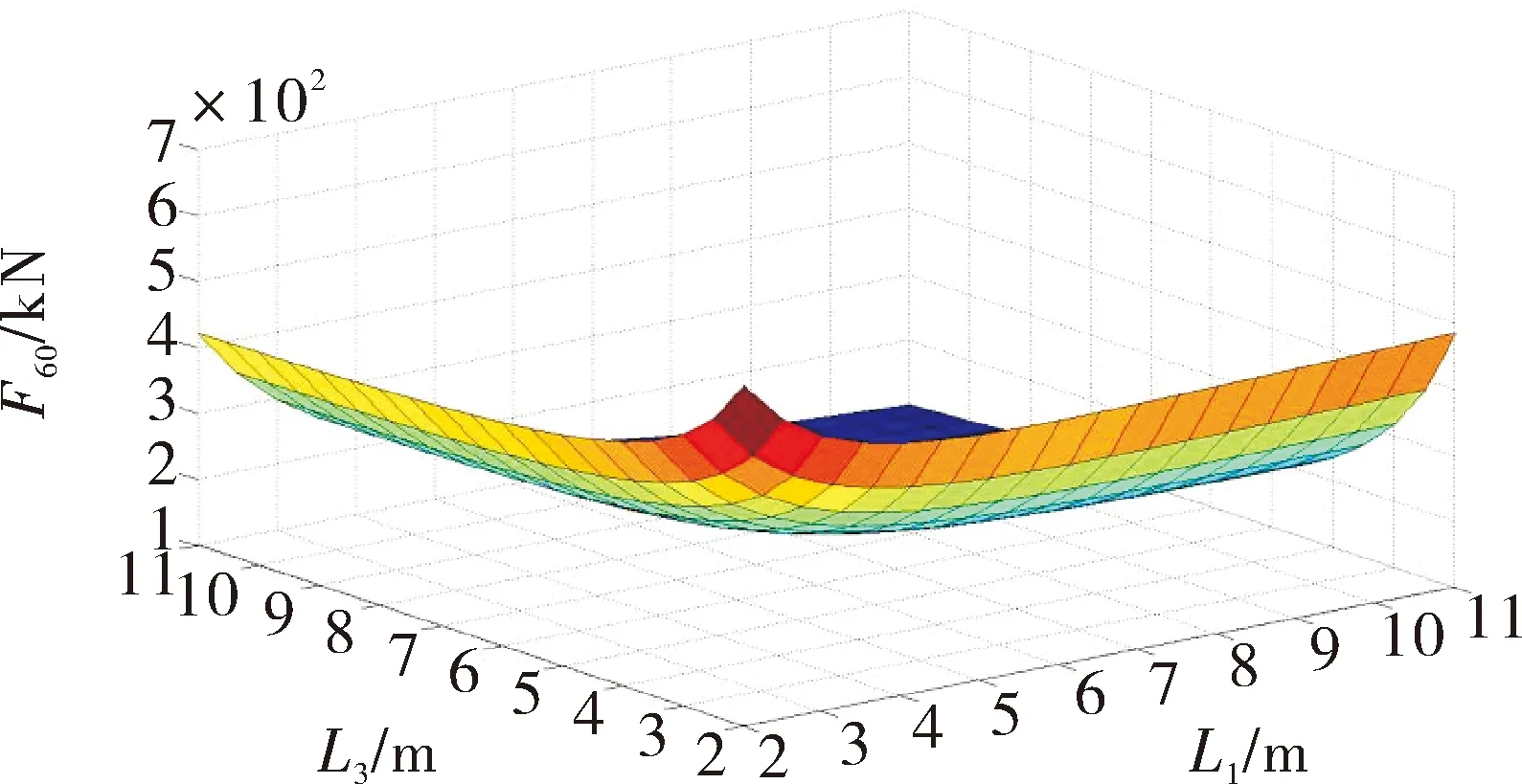
图5 起竖60°时的受力

4)当角度为75.45°时，该角度时重心几乎处于支点的正上方。L1和L3变化时对应缸的受力F75.45的三维图如图6所示。

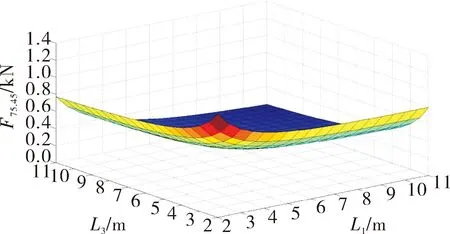
图6 起竖75.45°时的受力

5)当角度为90°时，L1和L3变化时对应缸的受力F90的三维图如图7所示。

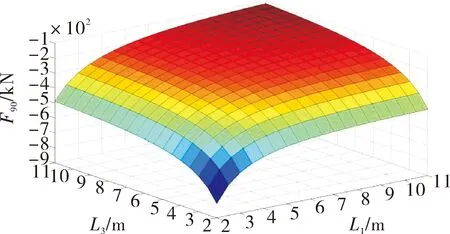
图7 起竖90°时的受力

3 起竖时间分析

快速性是起竖装置的重要指标[7]。这里起竖控制方案采用由起始位置到25°时，缸匀加速推进且加速度为a，到达90°前缸匀减速推进且加速度为2a，中间段缸匀速推进且速度为V。

设：功率为P；第一段所用时间为t1，对应缸的伸出长度为s1；中间段所用时间为t2，对应缸的伸出长度为s2；第三段所用时间为t3，对应缸的伸出长度为s3；总时间为t，总行程为s。

当θ1=0°时，得L8min为缸的初始安装长度；当θ1=90°时，得L8max为缸伸出时的最大长度，得：

(10)

(11)

s=L8max-L8min

(12)

t1=2×t3

(13)

(14)

s3=at32

(15)

s2=V×t2

(16)

s=s1+s2+s3

(17)

t=t1+t2+t3

(18)

V=at1

(19)

(20)

当θ1=25°时，代入式(5)～式(9)可求得F25的值，再联合上面的公式可求得功率和时间的关系。

利用MATLAB求解方程组[8]，并绘制当功率不同时，L1和L3变化时对应所需起竖时间的三维图。

1)当功率P为10 kW，L1和L3变化时对应所需时间t的三维图如图8所示。

2)当功率P为100 kW，L1和L3变化时对应所需时间t的三维图如图9所示。

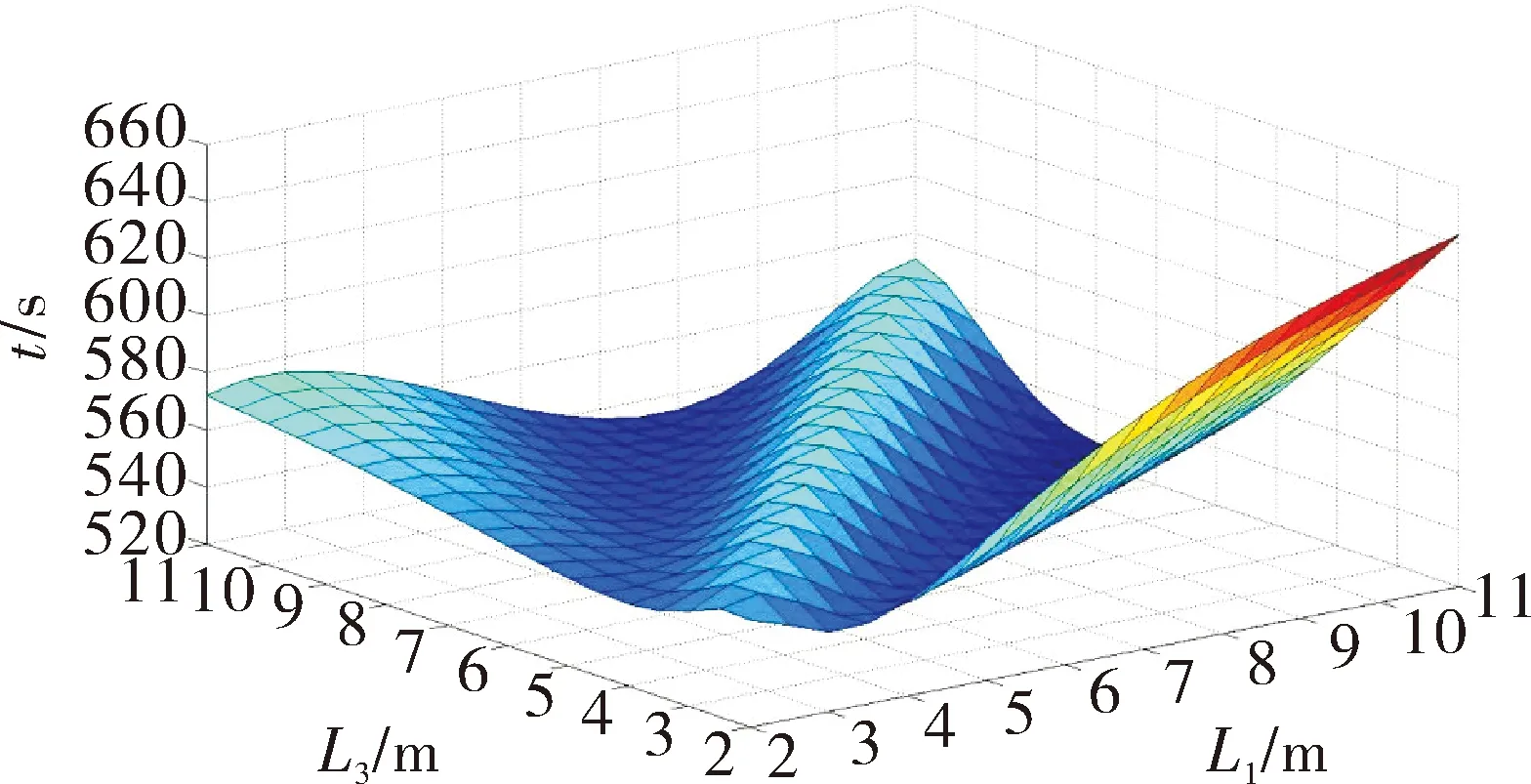
图8 功率10 kW时完成起竖所需时间

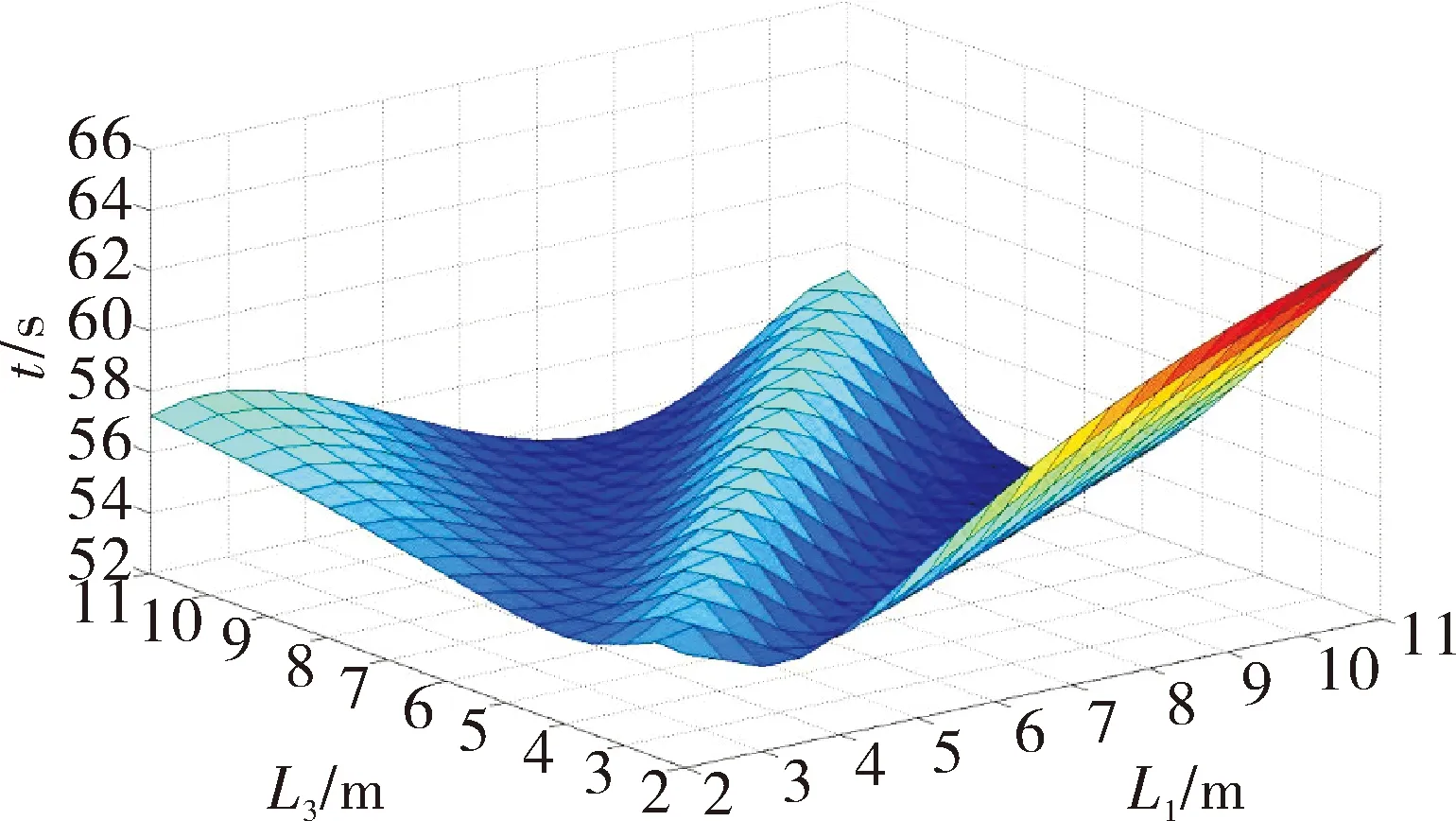
图9 功率100 kW时完成起竖所需时间

通过以上分析，可以得到缸的受力和功率时间曲线图，由于受缸初始安装长度L和行程限制，对上述分析进行优化，从而找到三铰点的最佳位置。

通过设定缸在初始位置时的最大推力小于1 470 kN；最大输出功率100 kW；全程(一次起竖)工作时间小于60 s。进行优化后的安装位置和初始载荷的曲线见图10，优化后的安装位置和全行程的工作时间曲线见图11，优化后的数据表见表1。

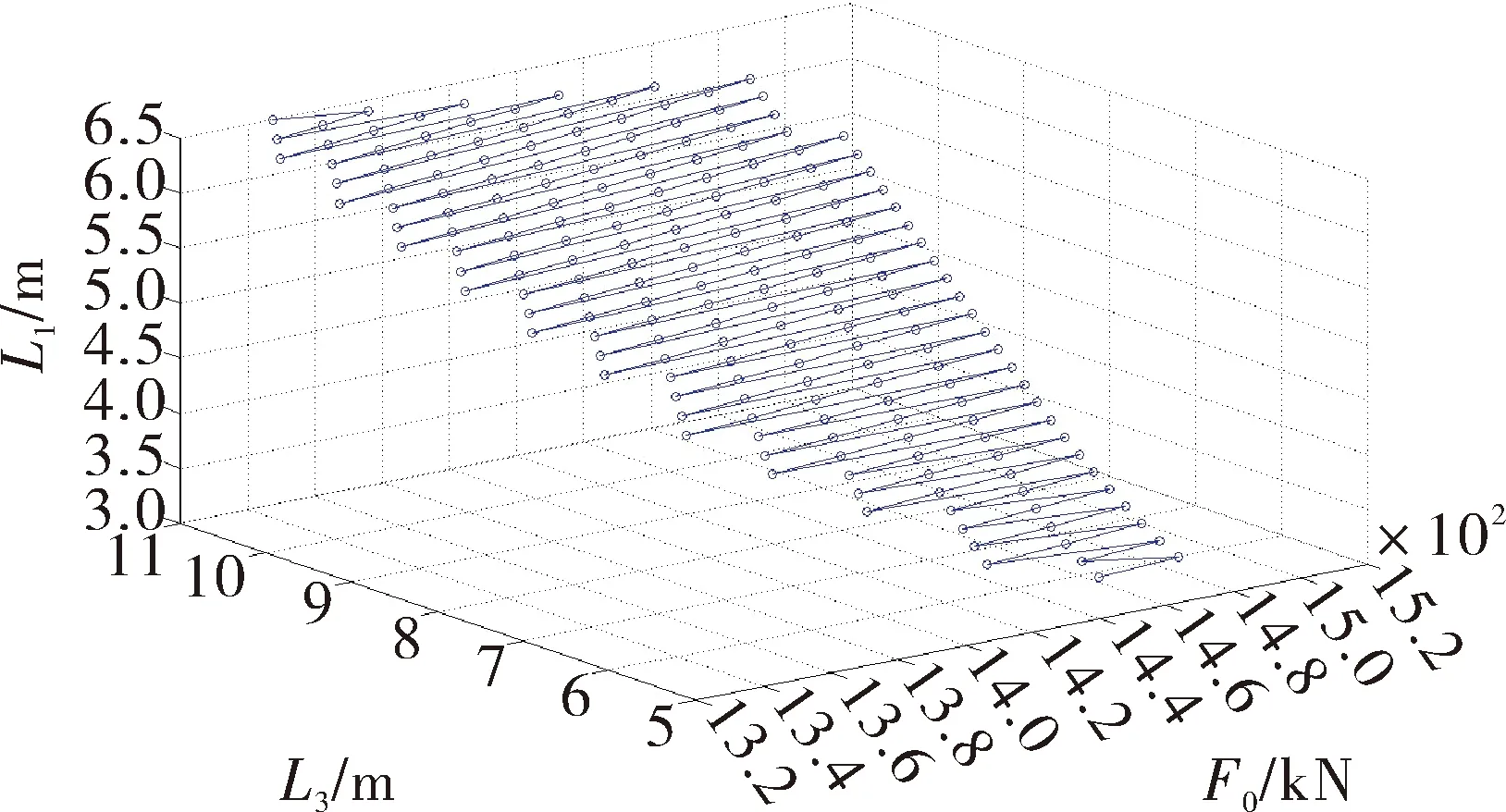
图10 优化后的安装位置和初始载荷曲线

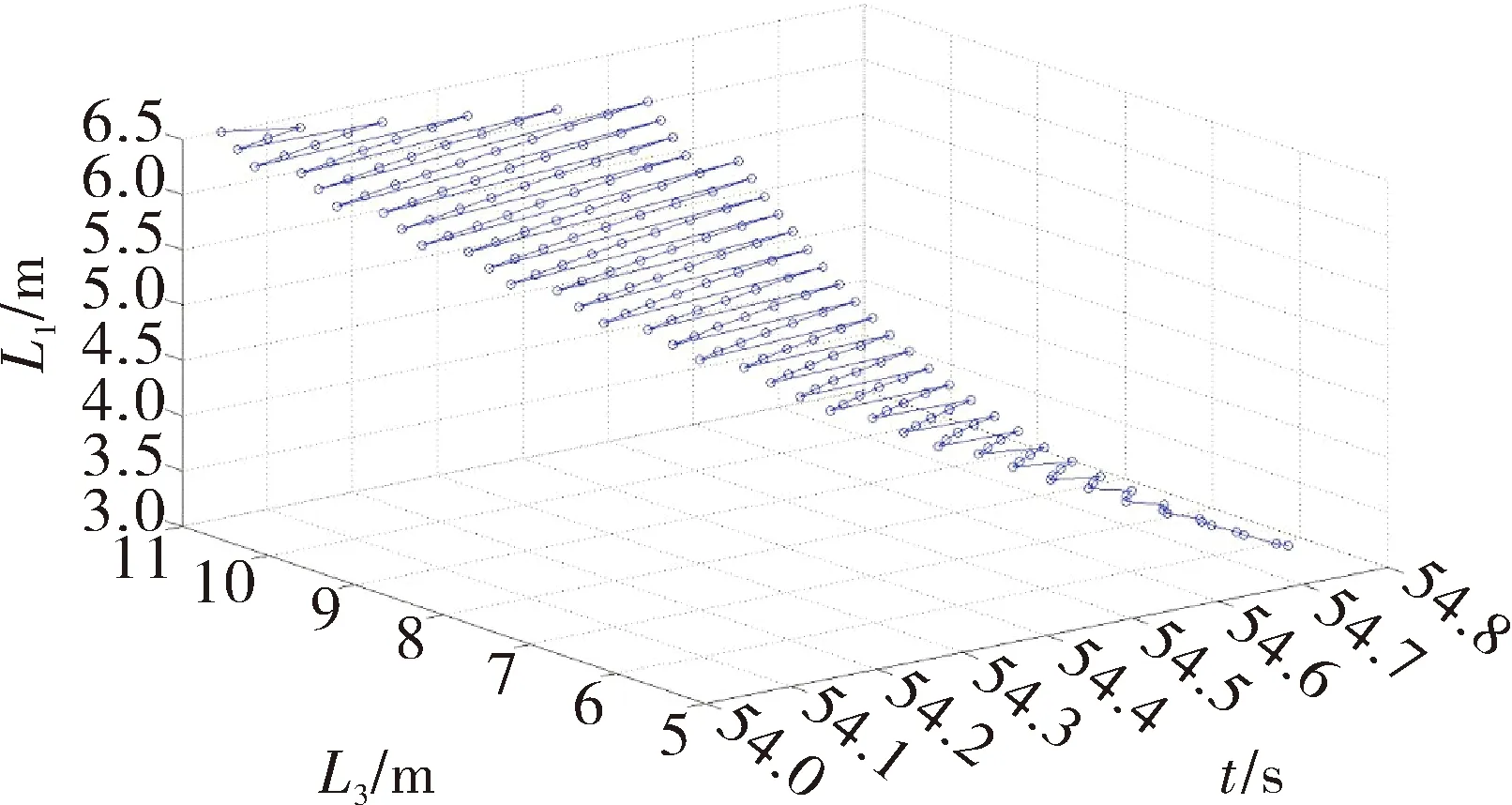
图11 优化后的安装位置和全行程工作时间曲线

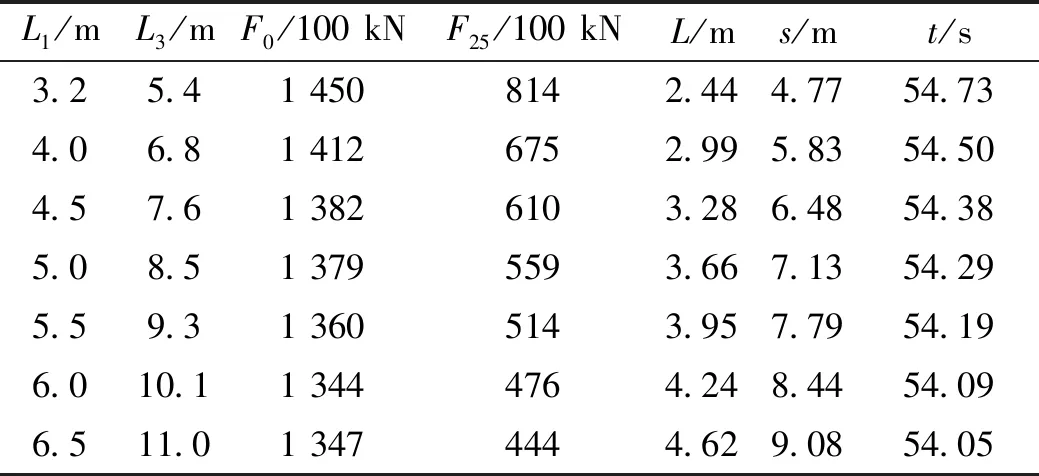
表1 优化后的数据表

4 结束语

针对典型的三铰点式二级缸驱动的导弹起竖装置进行了优化设计。通过对三铰点式起竖机构进行建模分析与仿真，既可以得出三铰点最佳位置关系，又能够给出驱动缸的驱动力和伸长比，有利于驱动缸的设计和整车布局设计。研究结果可为导弹起竖机构的优化设计提供参考，具有一定的理论意义和工程实用价值。