集对分析及分级贴近度模型在湖泊健康评价中的应用
2019-05-27吴明洋程家兴
吴明洋,程家兴
(1.重庆水利电力职业技术学院,重庆402160;2.淮安市水文局,江苏淮安223000)
0 引 言
湖泊健康综合评价可为湖泊系统修复和管理提供科学的方法[1],评价方法主要可归纳为确定性和不确定性方法,这些方法各有其优缺点[2]。目前,贴近度的公式有很多,常见的有海明贴近度、欧式贴近度、格贴近度等[3],贴近度公式必须符合贴近度的公理化要求[4],集对分析(SPA)[5]理论能够有效解决这类问题。高苏蒂等[6]将SPA理论与模糊逻辑理论相结合;周宇哲等[7]运用SPA理论解决了水环境得模糊性与不确定性;杨哲等[8]在色聚类模型中引入SPA理论。
为解决实际应用中贴近度差异性较小,无法做出准确判断的缺陷,本文将SPA理论引入到湖泊综合评价模型中,结合联系度与贴近度,采用指数型隶属函数,构造SPA与分级贴近度的耦合模型,并通过案例分析验证该模型的合理性和可行性。
1 湖泊健康评价指标体系的确立
湖泊健康综合评价的关键是确定评价指标体系,评价指标需要能够真实地反映湖泊的健康状况及变化趋向。本文将评价系统划分为4个层次结构[9],见图1。
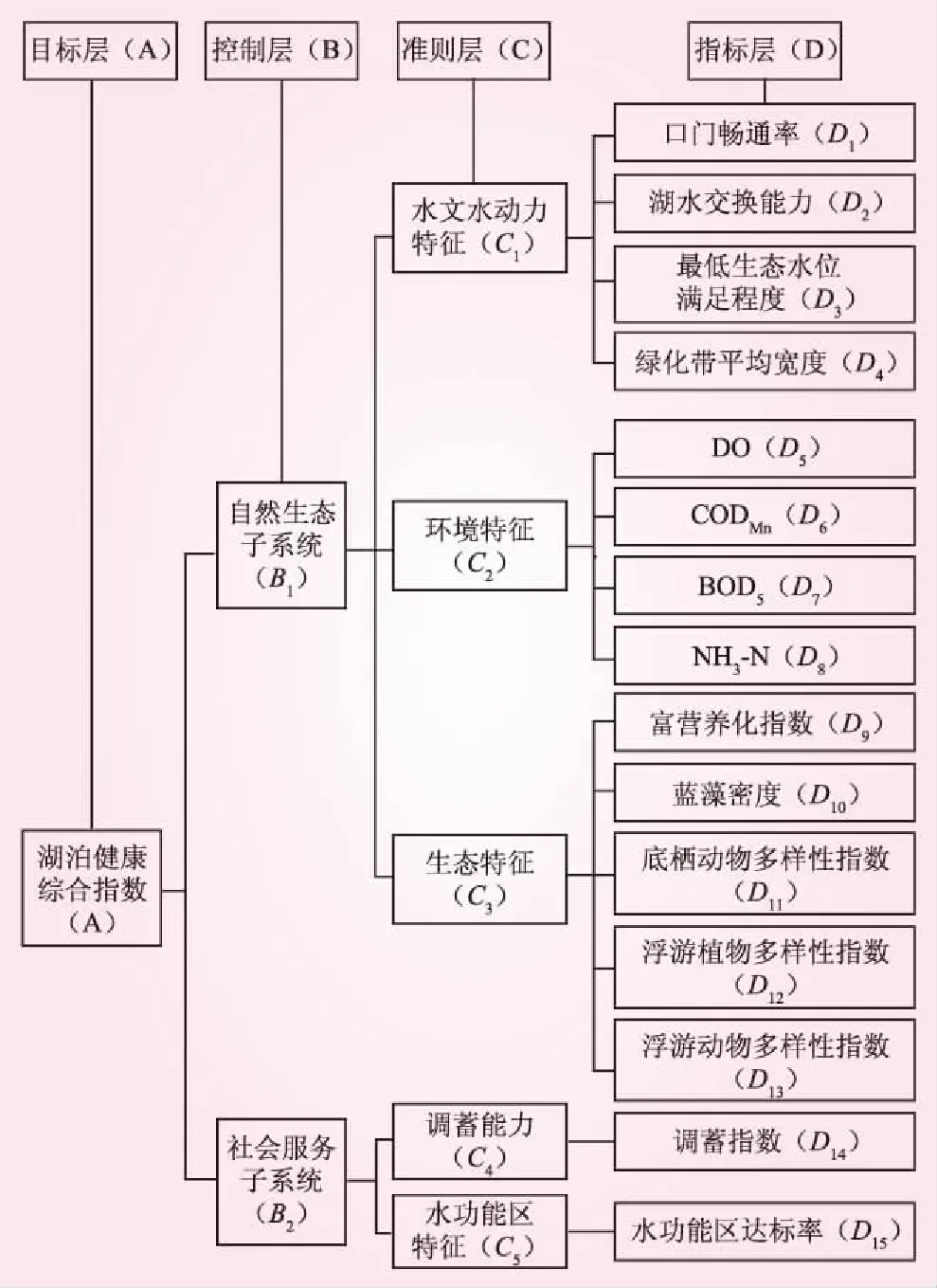
图1 湖泊健康评价指标体
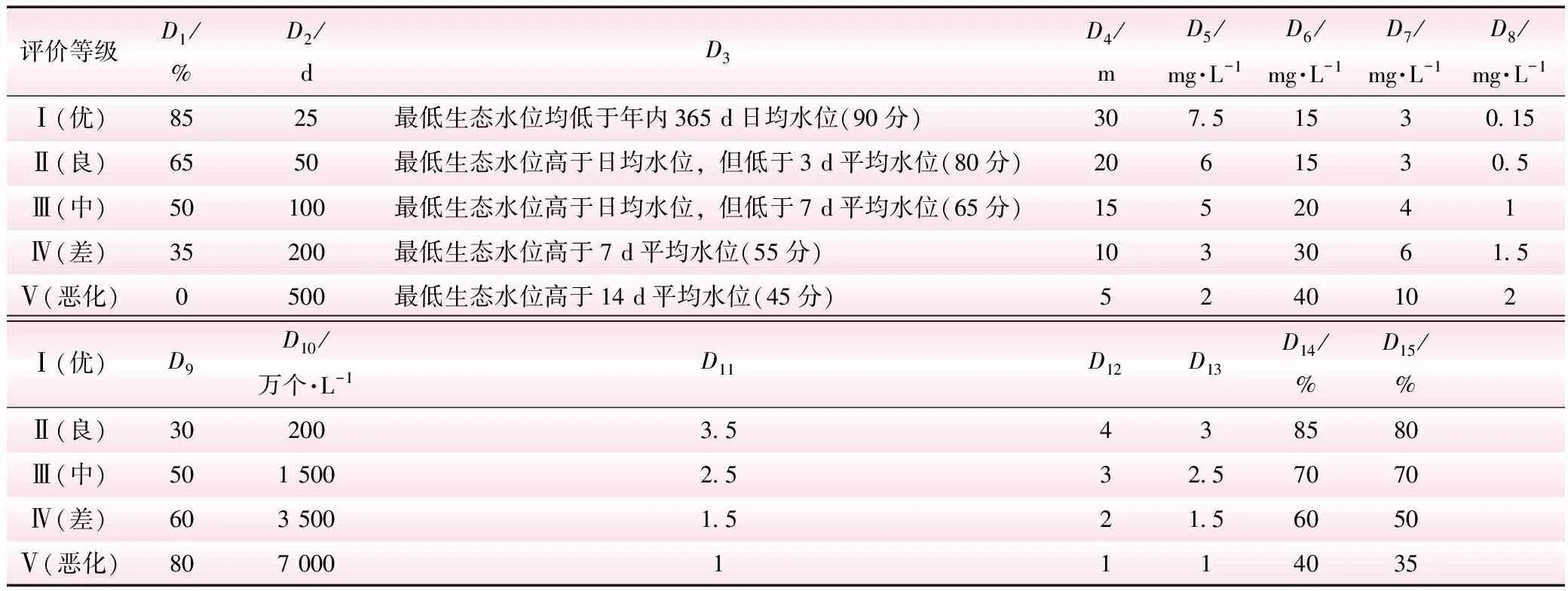
表1 评价指标分级标准
从图1可知,湖泊健康评价体系由目标层A、控制层B、准则层C及指标层D等4个层次构成。指标层D包含15个指标,主要包括口门畅通率(D1)、湖水交换能力(D2)、最低生态水位满足程度(D3)、绿化带平均宽度(D4)、DO(D5)、CODMn(D6)、BOD5(D7)、NH3-N(D8)、富营养化指数(D9)、蓝藻密度指数(D10)、底栖动物多样性指数(D11)、浮游植物多样性指数(D12)、浮游动物多样性指数(D13)、调蓄指数(D14)、水功能区水质达标率(D15)。
2 引入SPA理论的分级贴近度湖泊健康综合评价模型
2.1 隶属函数模型的确定
湖泊健康评价模型按照评价标准来建立隶属函数。
逆向指标隶属度计算。逆向指标表示指标值越小越好的指标,设μij为第i个样本的第j个指标对Ⅰ类标准的隶属度,则
μij=1x≤S1j
e-(x-S1j)2/γ2jSpj≤x
(1)
γj=1p∑pk=1Skj
(2)
式中,x为某指标的评分值;spj为第j个评价因子p级标准上限值;skj为第j个评价因子的k级评价等级的上限值;γj为第j个评价指标的参考标准值。
正向指标隶属度计算。正向指标表示指标值越大越好的指标,设μij为第i个样本的第j个指标对Ⅰ类标准的隶属度,则
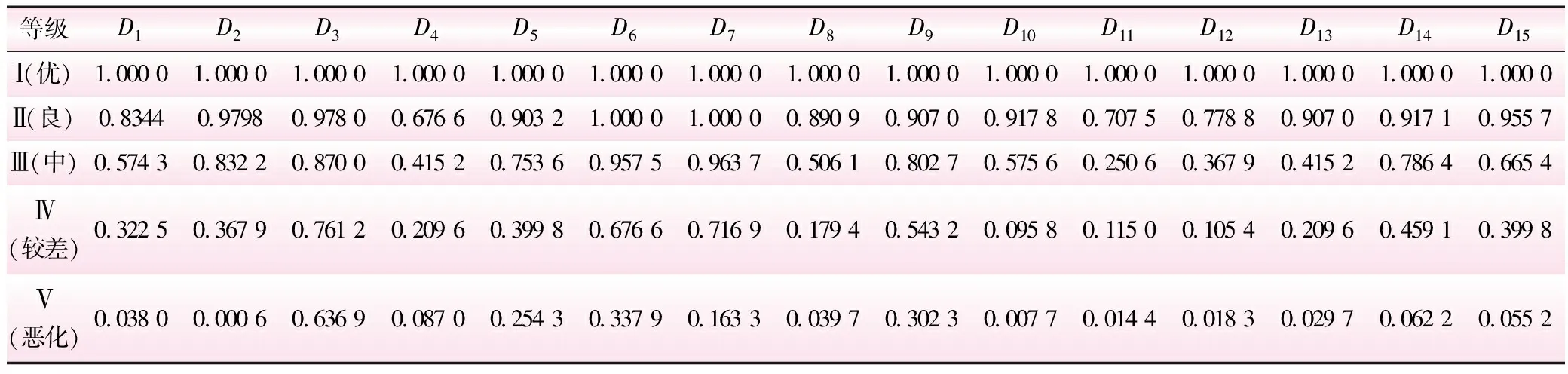
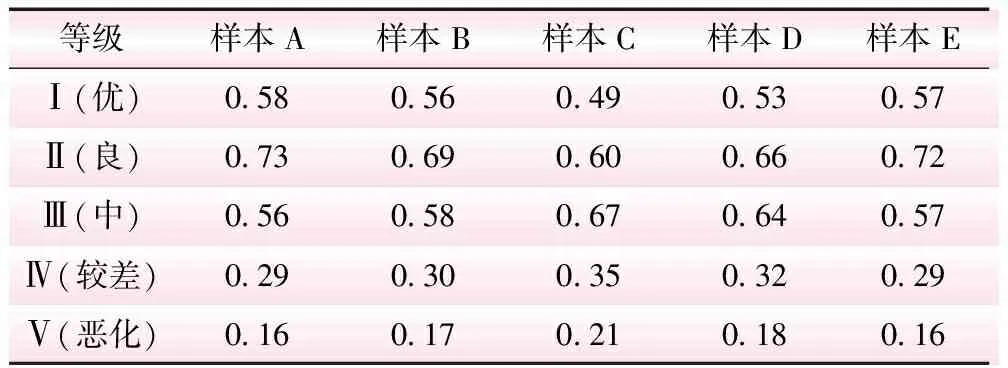
μij=1x≥S1j (3) 式中,skj为第j个评价指k级评价标准的下限值;spj为第j个评价指p级评价标准的下限值。 按下面的隶属函数确定各评价等级标准限值sk对Ⅰ类标准的分项隶属度kj,即 kj=e-(Skj-S1j)2/γ2j (4) 表2 湖泊综合健康评价指标实际值 表3 各评价指标对Ⅰ类(优类)标准的隶属度μij 表4 各指标各评价等级标准限值sk对Ⅰ类标准的分项隶属度kj 表4 各指标各评价等级标准限值sk对Ⅰ类标准的分项隶属度kj 等级D1D2D3D4D5D6D7D8D9D10D11D12D13D14D15Ⅰ(优)1.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 0Ⅱ(良)0.83440.97980.978 00.676 60.903 21.000 01.000 00.890 90.907 00.917 80.707 50.778 80.907 00.917 10.955 7Ⅲ(中)0.574 30.832 20.870 00.415 20.753 60.957 50.963 70.506 10.802 70.575 60.250 60.367 90.415 20.786 40.665 4Ⅳ(较差)0.322 50.367 90.761 20.209 60.399 80.676 60.716 90.179 40.543 20.095 80.115 00.105 40.209 60.459 10.399 8Ⅴ(恶化)0.038 00.000 60.636 90.087 00.254 30.337 90.163 30.039 70.302 30.007 70.014 40.018 30.029 70.062 20.055 2 假设各类评价等级所对应的模糊子集用sk(k=1,2,…,p)来表示,而样本评价因子的实际评分值所对应的模糊子集则用cii=1,2,…,m来描述,则综合贴近度公式如下 q(ci,sk)=1-di-δk (5) di=i-1=∑nj=1ωjμij-1 (6) δk=k-1=∑nj=1ωjkj-1 (7) 式中,di为各测点i与1之间的相对距离;δk为各评价标准等级隶属度向量k与1之间的相对距离;ωj为各评价指标的权重值。 择近原理[10]能解决贴近度大小相差不大或者相等的问题,而SPA主要用于解决不确定问题[11],其核心思想从同、异、反3个方面分析事物及系统[12]。联系系数公式如下 μi=ai1i1+ai2i2+ai3i3+ai4i4+ai5i5k=1,2,…,p (8) ai1+ai2+ai3+ai4+ai5=1i=1,2,…,m (9) aik=q(ci,sk)∑pk=1q(ci,sk) (10) 式中,ui为隶属度;aik为联系系数;q(ci,sk)为综合贴近度。 依据均分原则[13],将阈值范围[-1,1]平均分割成5份,得到4个评价等级的区间范围,具体评判为优、良、中、差、恶化。本文将层次分析赋权法(AHP)与熵值法结合起来,构造主客观赋权法来确定各指标的权重值。 某市有5个湖泊A、B、C、D、E,根据现场调研获取的数据,运用湖泊健康评价模型对2013年的湖泊健康进行评价。具体评价指标值参见表2。 根据表2实际指标值,运用引入熵权分析法的分级贴近度的湖泊健康评价模型对湖泊2013年的健康状况进行综合评价,隶属度μij计算结果参见表3,分项隶属度kj计算结果参见表4,综合贴近度q(ci,sk)计算结果见表5。 表5 各样本对应各类评价等级的综合隶属度q(ci,sk) 综合评价值μi结果如下:样本A为0.31、样本B为0.25、样本C为0.16、样本D为0.23、样本E为0.28。采用SPA和分级贴近度这2种方法对5个湖泊A、B、C、D、E的综合健康评价结果相同,分别为良、良、中、良、良,但传统贴近度模型按择近原理所得评价结果区分度较差,存在贴近度向量分量接近的现象,从而难以判别,湖泊评价等级数据可信度不高;而本文引入SPA的贴近度模型可以很好地弥补这种择近原理所造成的上述缺陷,能更准确地处理等级评价标准中存在的不确定信息,说明本文构造的模型实用性强。 本文采用指数型函数对传统隶属函数进行改进,扩大其信息覆盖范围,引入贴近度理论,同时引入SPA理论弥补贴近度法择近原理所存在的缺陷,结合主客观赋权法构建了基于SPA理论的分级贴近度湖泊健康评价耦合模型,并用该模型对样本湖泊进行综合评价,评价结果基本符合湖泊现状。
e-(x-S1j)2/γ2jSpj≤x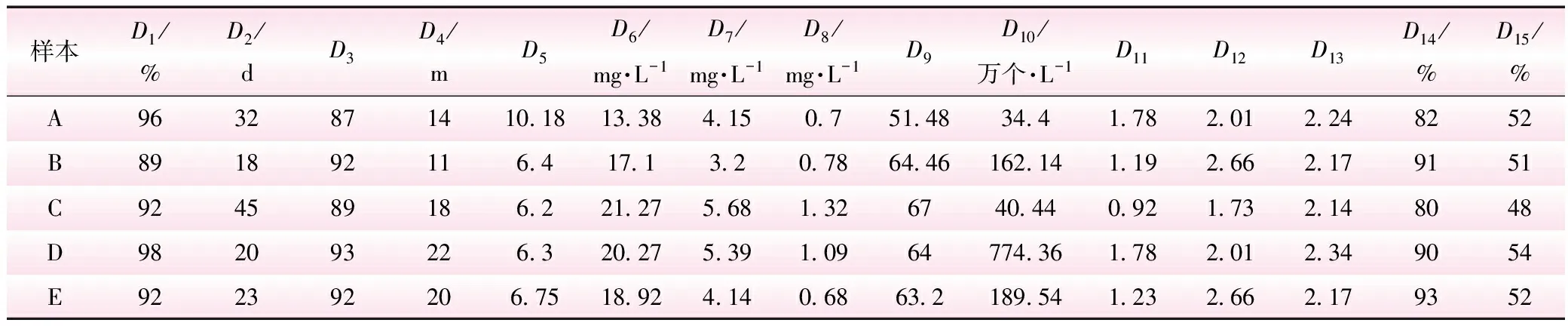

2.2 模糊贴近度的计算
(i=1,2…,m;k=1,2…,p)
(i=1,2…,m;j=1,2…,n)
(k=1,2…,p;j=1,2…,n)2.3 引入SPA的湖泊健康综合评价
3 案例应用分析
4 结 语
