红花丝采摘装置的凸轮机构运动失真研究
2019-05-27焦灏博曹卫彬孙胃岭李树峰杨双平
焦灏博,曹卫彬,孙胃岭,李树峰,杨双平
(石河子大学 机械电气工程学院,新疆 石河子 832000)
0 引言
2014 年,我国红花的种植面积超过 5.3 万 hm2,总产量占世界的80%以上[1],主要用于制药、食品加工、染料、油料和饲料等[2-3]。红花丝机械收获已经成为我国红花采摘的迫切需求,但现有的红花丝采摘装置采摘性能较低,主要表现为红花丝夹不紧导致漏采率较高,无法满足红花田间收获作业要求。其主要原因在于红花丝采摘装置的凸轮驱动机构在工作过程中存在较大冲击,导致出现运动失真[4-10],安装在推杆上的动齿与安装在主轴上的定齿在夹紧红花丝的过程中受到推杆与凸轮的冲击,使得动齿与定齿产生振动,导致弹簧施加给红花丝的夹紧力急剧减少,甚至夹不住红花丝,出现漏采现象。针对上述问题,建立了推杆在弹簧-凸轮作用下的动力学模型,并采用多项式函数设计凸轮型线。当凸轮型线对推杆的支持力始终小于弹簧对推杆的作用力时,可消除凸轮失真现象。由于凸轮运动失真发生在凸轮的回程段,通过MatLab软件对凸轮型线与推杆在弹簧作用下动力学模型进行编程,调节凸轮回程角与凸轮回程大小,消除凸轮机构失真现象。调整凸轮型线的参数发现:当凸轮行程大于红花丝采摘装置的动齿与定齿的张开间距、凸轮回程角大于动齿与定齿闭合需要的旋转角时,可以有效减少凸轮机构的失真现象;且当红花丝采摘装置的动齿与定齿张开间距为4.5mm、凸轮回程为5.8mm、动齿与定齿闭合需要的旋转角度为0.1π、凸轮回程角为0.14π时,三次多项式对应的凸轮型线未发生失真现象。
1 红花丝采摘装置工作原理与工作要求
红花丝采摘装置主要由轴承、机架、弹簧挡板、压缩弹簧、开口销、定齿、动齿、推杆、万向球、端面凸轮、带滑槽的定齿安装座、动齿固定板及主轴组成,如图1所示。其运动过程为:主轴、带滑槽的定齿固定座、定齿通过螺钉固定在一起;动齿固定在推杆上,并与推杆一起固定;推杆一端与弹簧连接,一端通过万向球与凸轮连接。主轴旋转的过程中带动动齿和定齿一起旋转,在凸轮与弹簧作用下,推杆带动动齿与定齿的张合,从而夹紧花丝,在动齿与定齿一起旋转的过程中拔掉红花丝。为了方便对红花丝采摘装置进行动力学分析,确保采摘装置采摘性能,对采摘装置的关键部件参数进行测试。其中,动齿的质量为1.50kg,推杆质量为3.25kg,弹簧刚度k=20N/mm,推杆中心到主轴的距离r=25mm。根据测试,推杆与带滑槽的定齿安装座之间的摩擦因数μ=0.2,拉拔掉一朵红花丝的力需25N,凸轮回程角θ0=18°。钢与红花丝之间的摩擦因数测试表明,红花丝与动齿、定齿的摩擦因数为0.5。采摘装置的转速不能低于8r/s,为保证较高的采摘效率与采净率,采摘装置转速取10r/s。
为了研究过程简单化,将红花丝采摘装置进行简化,如图2所示。图2中,在弹簧推动作用下,推杆带动动齿沿着主轴的轴线方向移动,与定齿闭合,夹紧红花丝;同时,主轴旋转,带动定齿和动齿绕着主轴沿着凸轮的型线旋转,实现红花丝的拉拔。因此,红花丝采摘装置在只有一个驱动的条件下,实现了对红花丝的夹紧与拉拔动作,且弹簧刚度、凸轮型线、主轴转速之间的匹配关系影响着采摘装置的工作性能。为提高红花采摘装置采摘红花丝的性能,需对弹簧刚度、凸轮型线及主轴转速之间进行动力学分析。
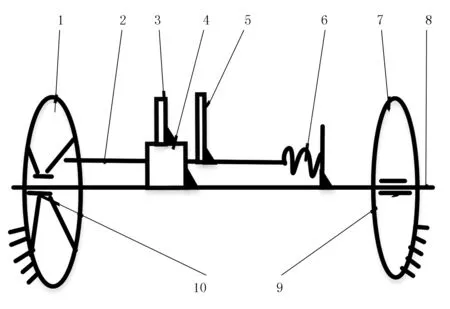
1.凸轮 2.推杆 3.定齿 4.主轴与推杆构成移动副 5.定齿 6.弹簧 7.支座 8.主轴 9.主轴与支座构成转动副 10.主轴与凸轮构成转动副
2 夹花过程的推杆运动位移建模
红花丝的夹紧发生在凸轮的回程段,在弹簧的推动下,推杆在绕着主轴旋转的过程中沿着轴向移动,带动采摘红花丝的动齿移动,与安装在机架上的定齿闭合夹紧花丝。为了研究方便,将推杆沿着凸轮型线的旋转运动转化为沿着凸轮型线移动,因此在凸轮回程段采摘装置运动过程将转化,如图3所示。

1.主轴 2.弹簧 3.推杆 4.凸轮
device in the cam return-stroke
图3中,v为1、2、3构件沿着凸轮型线的前进速度;F弹为弹簧弹力;Ff凸轮对推杆的摩擦力;FN凸轮对推杆的支持力;F凸轮为凸轮对推杆的作用力的合力。
将动齿质量视为推杆质量的一部分,定齿质量视为主轴质量的一部分,推杆以角速度w绕着主轴轴心以半径为r的旋转运动转化为以线速度为v=wr沿着凸轮回程型线移动。为了保证推杆能够始终与凸轮回程型线接触,需要在凸轮的线约束下,对弹簧推动推杆的运动状态研究,建立了弹簧推动推杆运动的动力学模型,如图4所示。图4中,F弹为弹簧对推杆的弹力,m为推杆质量,F凸轮为凸轮对推杆的作用力的合力。

图4 弹簧推杆的动力学模型
推杆的合力F等于弹簧弹力F弹=K(x0+x)减去凸轮支持力F凸轮。其中,x0为弹簧初始压缩量,由于拉拔掉一朵花丝需25N的力,因此需要的弹簧压缩量Xj=25N/(0.5×K)=2.5mm,x为推杆运动位移,即
F=K(x0+x)-F凸轮
(1)
当弹簧对推杆的弹力大于凸轮对推杆的支持力(即K(x0-x)>F凸轮)时,推杆的运动将不会脱离凸轮面。由于凸轮支持力F凸轮与凸轮型线曲线函数f(s)的二次导数、推杆质量成正比例关系,其表达为
(2)
式(1)、式(2)可以得出推杆运动位移与凸轮型线的关系为
(3)
其中,f(θ)表示凸轮型线与凸轮角位移θ的变化关系。
假设在没有凸轮支持力F凸轮的作用下推杆的自由位移为x(t),则
(4)
其中,h=4.5mm为动齿与定齿张开时候的间距。通过对式(4)进行求二阶导数,与式(1)得到推杆运动微分方程为
(5)
通过二阶非齐次微分方程的解法,求得推杆运动位移x(t)的数学模型为
(6)
由图3可得出推杆沿着凸轮轨迹运动对应的角位移θ及w(推杆绕着主轴的转速),二者之间的关系为
θ=wt
因此,将推杆自由位移x(t)转化为角位移函数x(θ),即
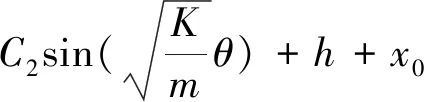
(7)
其中,C1、C2通过边界条件求解。
当推杆在凸轮回程的最顶端时,θ=0,x(w)=x0,带入式(7)得
C1=0
(8)
在凸轮回程的最低端时,假设θ=θ0,x(w)=x0=2.5mm,则
(9)
由式(6)~式(9)得,采摘装置推杆自由运动的位移为
x(θ)=-7.5sin(2.05θ)+7
(10)
由于推杆的自由位移x(θ)大于推杆受凸轮支持力的位移x,因此由式(3)与式(10)可得
(11)
式(11)为红花丝采摘装置驱动机构的凸轮型线不失真的理论条件,为凸轮型线的设计合理性提供了理论基础。
3 保真条件下的凸轮型线设计与试验
3.1 凸轮回程型线设计条件分析
采用三次多项式、五次多项式、七次多项式对凸轮回程型线设计,以便选取最优多项式凸轮型线轨迹方程,其表达式为
(12)
(13)
(14)
通过对式(12)~式(14)求导得出凸轮型线对推杆的不同多项式加速度为
(15)
(16)
(17)
利用MatLab软件绘制3种多项式对应的加速度与弹簧对推杆的加速度进行对比,如图5所示。当凸轮对推杆产生的加速度小于弹簧对推杆的加速度时,即满足式(11)凸轮不失真的条件。当凸轮的回程角度为0.14π、凸轮的回程为5.8mm时,推杆在弹簧推动下的加速度均大于三次多项式的凸轮型线,未发生失真现象。五次多项式与七次多项式均大于弹簧对推杆的加速度(即出现了凸轮型线失真),因此三次多项式作为凸轮回程型线的最佳函数。
通过对图5进一步分析可知:当凸轮的基圆半径与推杆的质量一定时,凸轮型线对推杆的加速度曲线与弹簧对推杆的加速度的曲线围成的面积越大,则凸轮与推杆的摩擦力做的越大,凸轮表面的磨损越严重。通过3种多项式的比较发现:三次多项式对应的凸轮型线磨损最小,摩擦力做的功也最小。因此,保真凸轮机构的运动不失真,不仅能实现提高红花丝采摘装置的性能,还可以降低红花丝采摘装置的能耗。
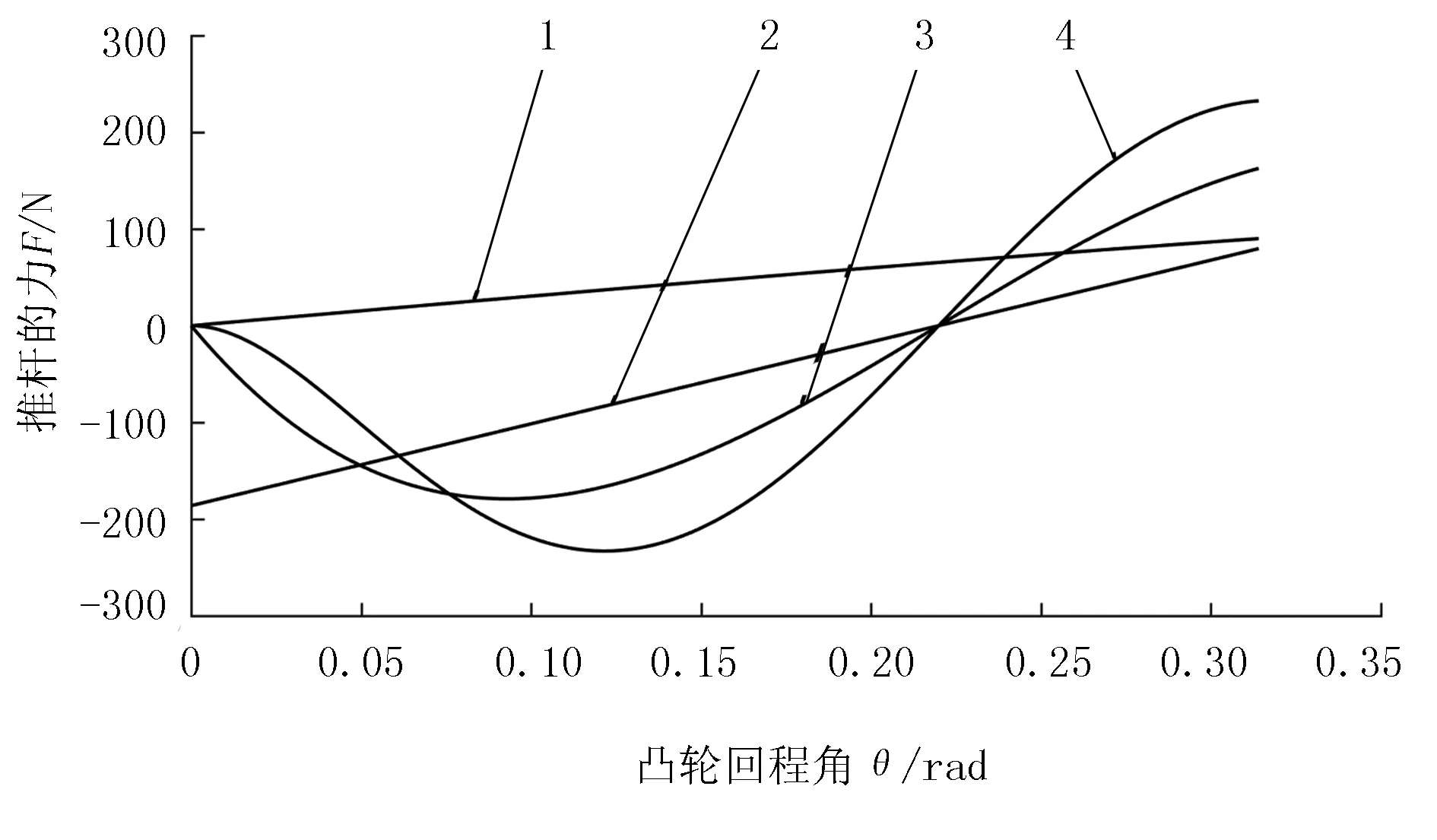
1.弹簧对推杆的力 2.三次多项式凸轮型线曲面对推杆的力 3. 五次多项式凸轮型线曲面对推杆的力 4. 七次多项式凸轮型线曲面对推杆的力
3.2 凸轮回程型线设计
当凸轮型线满足凸轮动力学要求时,还应满足红花丝采摘装置的工作要求。采摘红花丝时,推杆的转角为18°(即0.1π),动齿与定齿的间距为4.5mm。为满足动力学的设计要求,保证凸轮机构运动的不失真,将凸轮回程角设计为0.14π。对凸轮的型线进行运动学校验,即满足当凸轮型线在凸轮回程角位移为0.1π时,凸轮的回程位移应该大于等于4.5mm。通过MatLab软件对位移方程进行编程,如图6所示。
图6 凸轮回程型线函数程序
通过多种多项式方程进行轨迹仿真,如图7所示。通过分析发现,三次多项式对应的凸轮回程轨迹也最为理想。

1.七次多项式的凸轮型线 2.五次多项式对应的凸轮型线 3.三次多项式对应的凸轮型线 4.推杆在弹簧作用下的自由位移
3.3 凸轮升程型线设计
凸轮升程在近休止与远休止衔接处应光滑过渡,避免机械运动冲击,要求凸轮的升程对应的型线两端点都连续可导,即满足各自的端点处速度与加速度均为零。为此,采用五次多项式进行设计,且凸轮型线采用对称结构设计。凸轮回程角范围为[0,0.14π],则近休止角与回程角和为π,近休止角为0.86π;为了保证升程段推杆运动平稳,取升程角为π/3,则远休止为2π/3。采用MatLab绘制凸轮型线如图8所示。
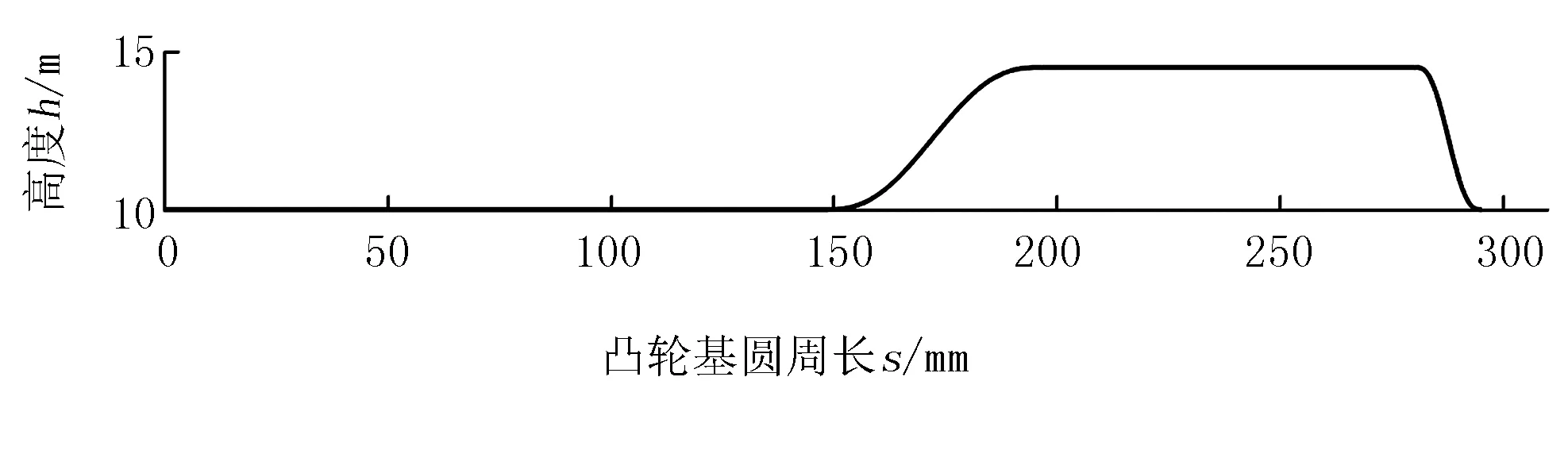
图8 凸轮型线
通过Creo软件绘制凸轮的三维模型如图9所示。
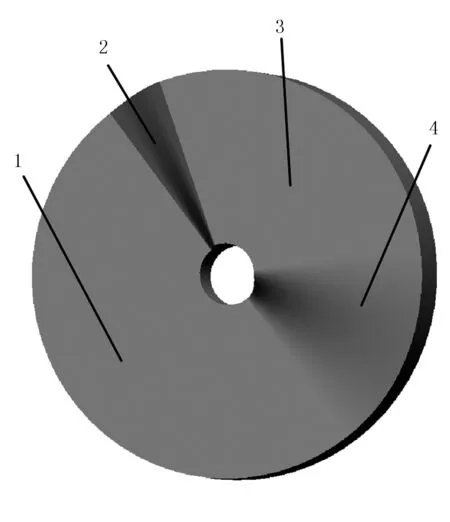
1.近休止 2.凸轮回程 3.凸轮远休止 4.凸轮升程
对红花丝采摘装置的推杆在凸轮断面的运动进行仿真,如图10所示。由图10可以看出:在凸轮型线的作用下,推杆运动速度连续。
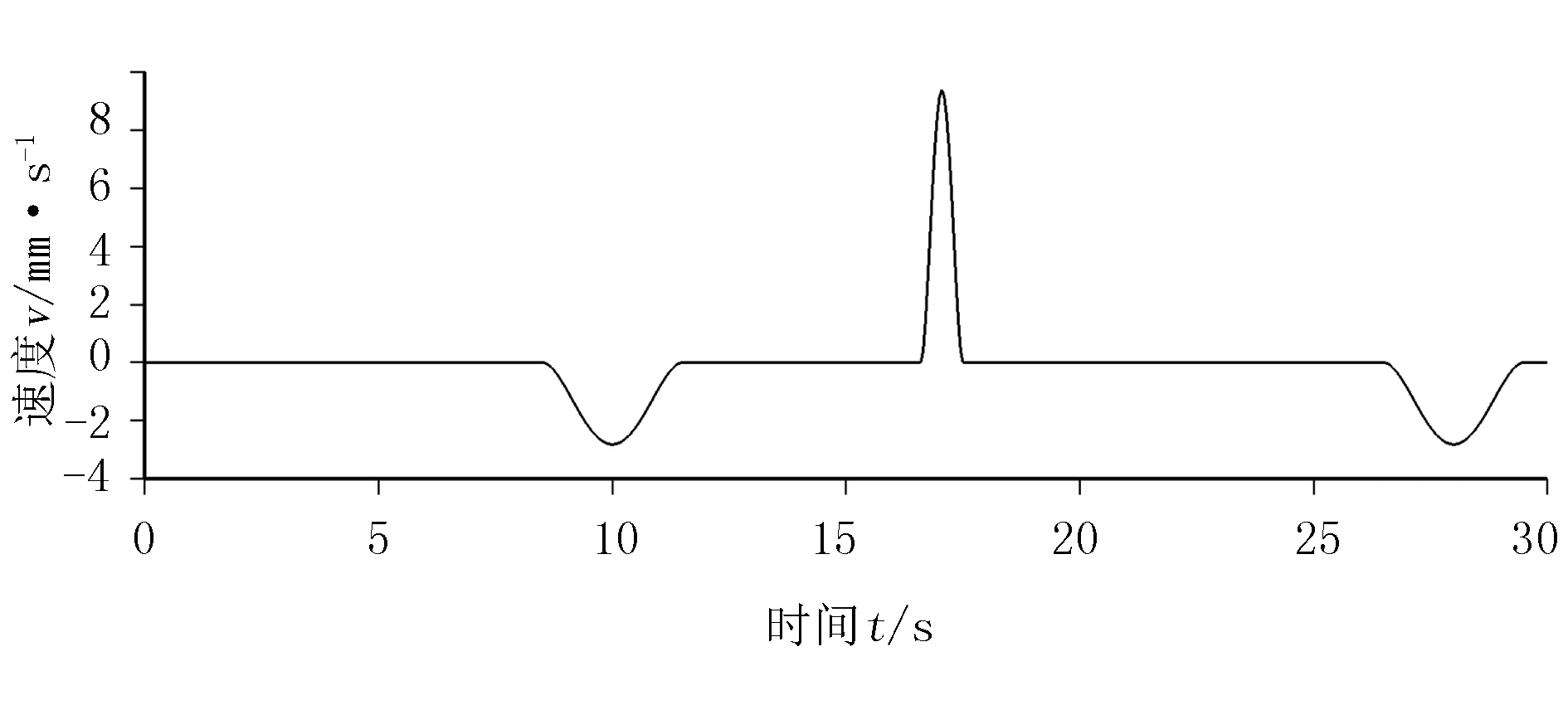
图10 推杆运动速度分析
对推杆运动的加速度测试,如图11所示。图11中,未发生跳跃,说明推杆在凸轮型线运动的过程中不会脱离凸轮型线。

图11 推杆加速度分析
3.4 台架试验
对凸轮的三维模型进行加工,安装于红花丝采摘装置,通过高速摄像对推杆在凸轮面的运动情况进行测试,如图12所示。

1.电机 2.链轮 3.供电箱 4.弹簧 5.主轴 6.采摘红花的动齿与定齿 7.推杆 8.凸轮
电机通过链轮带动主轴旋转,在弹簧的作用下,推杆绕着凸轮的端面进行转动。当主轴的转速为10r/s
时,通过高速摄像机对推杆在凸轮面上的运动情况进行观测,结果未发现推杆脱离凸轮,消除了采摘红花丝的动齿与定齿产生振动,有效地避免红花丝采摘装置的漏采,提高了红花丝的采净率。
4 结论
1)由于凸轮型线设计不合理,造成凸轮机构运动失真。为避免该现象出现,凸轮对推杆的力应小于弹簧对推杆的作用力,以消除凸轮机构的运动失真。
2)为保证红花丝采摘装置采摘性能,通过MatLab软件对推杆在弹簧与凸轮作用下的动力学模型进行分析,结果表明:动齿与定齿闭合需要的旋转角应小于凸轮的回程角,凸轮回程的行程应该大于动齿与定齿张开间距;当凸轮的回程为5.8mm、回程角为0.14π时,三次多项式对应的凸轮回程型线不会造成运动失真。
3)高速摄像试验表明:当红花丝采摘装置的转速为10r/s时,红花丝采摘装置的推杆未脱离凸轮面。由此验证了该设计理论的正确性。
