基于改进布谷鸟算法-BP神经网络的松茸发酵过程软测量建模

朱湘临，宋 彦，王 博，丁煜函，朱 莉，姜哲宇2，陈 威

(1.江苏大学 电气信息工程学院，江苏 镇江 212013；2.无锡太湖水务有限公司，江苏 无锡 214000)

0 引言

松茸作为一种珍贵的食药两用真菌，因其自身特有的抗肿瘤、抗衰老、改善免疫系统功能等功效而大受人们喜爱[1]。随着我国对松茸需求量的日益增大，传统的培养方式已远远不能满足人们对松茸的需求。松茸液态深层发酵和其他传统生产方式相比，具有菌丝体生长周期短、产量高、污染小等优越性，并且通过液体深层发酵获得的菌丝体在营养价值上与野生子实体相近。然而，由于发酵过程的高度时变性和不确定性，目前，关键生物参量还难以实时在线测量。通常将发酵液于3500r/min离心20min，菌丝体经去离子水反复洗涤，离心多次，取沉淀物于60℃烘干至衡重，用分析天平沉重。离线化验时滞性很大，并且在线取样容易引入人为污染，会降低发酵品质,无法满足现场实时优化控制的需要。因此，软测量技术的引入是解决上述问题的有效途径[2-5]。

BP神经网络(BPNN)[6]软测量是近年来应用很广泛的一种数据驱动软测量方法，因其优良的非线性逼近能力，已被广泛地应用于微生物发酵过程的软测量建模中[7]。但是传统BPNN在发酵过程软测量实际应用中存在以下问题：

①其算法本质为梯度下降法，权值修正时收敛缓慢，易陷入局部最优；

②初始权值和阈值为随机选择，缺乏理论依据。

国内外学者在这方面做了许多研究，花亚梅等[8]将动量和自适应调节学习率引入BPNN，对其进行改进，增加了沼气厌氧发酵的稳定性、缩短了训练时间；杨强大等[9]改进了传统BPNN的误差函数，由此在一定程度上克服了用传统BPNN对诺西肽建模的过拟合现象；迟雷等[10]采用添加动量项和可变学习速率的方法对BP算法进行改进，提高了发酵过程的预测精度；以上对传统BPNN的改进，都是对权值修正公式进行了改进，一定程度上提高了预测精度，但是还存在着初始权值和阈值选择不当而陷入局部最小值的问题。文献[11]强调在多峰值优化过程中，布谷鸟搜索算法(CS)相对于粒子群算法和遗传算法更容易获得最优解；国内外研究者也已将CS优化BPNN运用到短时交通流量预测[12]、微波加热温度预测模型[13]、网络流量预测[14]、神经网络图像复原[15]、股价预测[16]等。以上这些运用布谷鸟算法优化BPNN虽然具有较好的全局性能和收敛速度[17]，然而在局部搜索能力上稍有欠缺[18-23]。同时这些智能优化算法只能得到BPNN的一个参量初值，之后的参量更新依靠传统BPNN的自身修正。

为解决上述存在的这些问题，提出了一种基于改进CS优化改进BPNN的软测量建模方法。将两阶段发现概率的改进CS和运用附加动量与动态学习率的改进BPNN相结合，以松茸发酵过程中难测量为对象，建立软测量模型。仿真结果表明，改进的CS-BPNN软测量模型预测精度提高了6%以上，能够满足松茸发酵过程中实时在线测量的需求。

1 算法描述

1.1 BP算法的改进

传统BP算法的权值更新公式为：

w(i+1)=w(i)+Δw(i+1)

(1)

引入附加动量和动态调整学习率对BP算法进行改进，附加动量法的改进以传统BP算法的权值更新公式为基础，其在每个权重的变化上加上一项正比于上次权重变化量的值，由此得到新的权值。其权值更新公式为：

w(i+1)=mc×w(i)+μ×Δw(i+1)

(2)

式中，mc为动量因子、μ为学习率，都取0～1之间的数。

动态调整学习率进行的规则为：检验权重修正值，倘若能将误差函数减少，就代表此学习速率值较小，那么增大它；倘若不能，就减小它的值。它的调整公式为：

(3)

式中，μ为学习率，当权重修正值使误差函数E(i)降低时，增大μ；相反，则减少。

1.2 布谷鸟算法的改进

布谷鸟算法是由模拟布谷鸟借窝产卵的繁衍习性与飞行方式转变得到的[24]，它属于第3种新型仿生群智能算法。布谷鸟算法采用莱维飞行更新布谷鸟鸟巢位置，莱维飞行(Lévy flight)是具有截尾概率分布步长的随机游走[25-27]。此外，布谷鸟算法要遵守3个准则：①一只布谷鸟一次仅分娩一只蛋，并且随机挑选鸟巢孵化；②相对最优的鸟巢能够保留到下一代；③鸟巢总个数是固定的，鸟窝主人有概率pa发现外来鸟蛋。在上面3个准则下，布谷鸟算法使用Lévy飞行实现位置更新的公式为：

⊕L(λ)i=1,2,...n

(4)

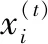
(5)

布谷鸟算法虽然拥有较好的全局性能，可它的收敛速度和局部搜索能力却还存在问题。在布谷鸟算法里，pa为十分关键的参量，优异的pa能够使算法的全局搜索能力与局部搜索能力得到平衡。因此从pa入手对传统布谷鸟算法进行改进，具体为将原固定发现概率改进为两阶段动态发现概率。第一阶段以全局为主、局部为辅，第二阶段以局部为主、全局为辅。实现方法：在算法前Nmax/2(Nmax为最大迭代次数)里保证pa值逐步降低，使得布谷鸟可以搜寻新的鸟巢，pa选取负正弦自适应递减策略；而在后Nmax/2里使布谷鸟在现鸟巢附近搜索更优异的鸟巢，pa选取负余弦自适应递减策略。具体公式为：

(6)

式中，pamax和pamin分别表示发现概率的最大值和最小值；Nmax和Ni分别表示迭代次数的最大值和当前迭代值。

2 松茸发酵过程软测量建模

2.1 辅助变量选择

在建立松茸发酵关键参量软测量模型之前，必须对发酵机理进行分析[28]，确定合适的辅助变量。在松茸发酵过程中，既对主导变量(菌丝生物量)有影响，又易于在线实时测量的有：空气流量q、发酵罐压力p、发酵罐温度T、发酵液体积V、CO2释放率CER、氨水流加速率η、葡萄糖流加速率l、溶解氧DO、电机搅拌速度r、发酵液酸碱度pH。

(7)

式中，k为采样时刻，μij是两个变量的相关系数，si是不易测变量数据组，sj是可测变量数据组，m为样本大小。

(8)

式中，λij(k)是变化率相关系数，M为取样个数，ζk是符号因子，rij是关联度，β是数据变化率对关联度的影响。

通过一致关联度法，根据公式(7)、(8)得到环境变量数据和主导输出变量之间的关联度，具体的计算数值结果如表1所示。

表1 环境变量和主导变量的关联度

关于辅助变量的选取数量，过多会导致模型复杂，增加模型学习训练的时间；过少会导致模型学习能力差，预测结果不准确。本文选择关联度最高的前4个作为辅助变量，即电机搅拌转速r、空气流量q、溶解氧DO、发酵液酸碱度pH。因此该软测量的主导变量与辅助变量之间的模型为：

φ(X)=f(pH,r,q,DO)

(9)

2.2 改进CS-BP的软测量建模

鉴于改进后，CS的全局搜索能力和局部搜索能力会更加突出，更易适合用来优化BPNN的构架。我们将BPNN看作改进CS算法的适应度函数，那么即可利用算法自身全局寻优能力强的优势去寻觅初始的权值与阈值组合，进而把获得的最优神经网络结构运用到实际发酵过程。

改进的CS-BPNN软测量模型的算法如下：

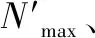
(3)根据公式(6)对pa进行更新，产生服从均匀分布的随机数r∈(0,1)，与pa进行对比，若r>pa，就将鸟巢位置随机变化，若r

(5)将获得的最优解向量进行反编码操作，提取出BPNN的权值和阈值之后根据输入输出就可建立改进的CS-BP模型。

(6)计算均方误差E，若E≤ε，则保存对应的权值。若不是，则计算出权值的改变量ΔW，具体过程如同传统BPNN一样。

(7)将ΔW代入公式(2)得到新的权值，对比先后两次均方误差E，按公式(3)调整学习速率μ。

3 实验与仿真

按照工艺要求，本次取用100 L发酵罐，装液量为70 L，将发酵罐进行高温蒸汽灭菌，发酵过程温度控制在25 ℃±1 ℃、通气量为0.7 (V/V·min)、接种量为8%、发酵罐压控制在0.3～0.5 MPa。搅拌电机带动搅拌轴旋转，搅拌转速设为200 rpm。菌丝体经去离子水反复洗涤、离心多次，取沉淀物于60 ℃烘干直到恒重，采用分析天平就可获取菌丝生物量。由于发酵过程中的初始生物量过小，我们一般不测量。在正常发酵条件下，每次采样间隔3小时同时离线测量菌丝生物量。汇集现场数据进行数据预处理，一共采集15个发酵批次的数据，从上述批次中拿出3批(包含180个样本)作为测试样本，其余12批数据(包含720个样本)作为训练样本。

图1 菌丝生物量预测曲线

从预测结果拟合程度能够发现，改进型CS-BPNN软测量模型相比传统BPNN软测量建模，具有更强的预测能力。比较两种软测量模型的菌丝生物量误差曲线如图2所示。

图2 菌丝生物量误差曲线

根据图中曲线，能够轻易的发现，改进CS-BPNN模型的预测值与实验值之间的误差要比传统BPNN小得多，拟合程度也高很多。

表2为松茸发酵过程中菌丝生物量用改进CS-BPNN和传统BPNN软测量模型预测输出的误差对比情况。由表能够轻易发现，对于第一批测试样本，改进CS-BPNN模型下样本均方根误差(RMSE)为0.247 7，明显低于传统BPNN均方误差0.581 4。其他两批测试样本，传统BPNN的均方误差也明显高于CS-BPNN，表明了改进CS-BPNN建模的预测性能更为优越，稳定性更强并且精度更高。由于采用离线软测量建模，在实际应用中离线建模速度并是很重要，因此此处不做详细说明。

表2 两种模型误差对比

4 结束语

针对松茸发酵过程的关键参量(菌丝生物量)难以在线测量的问题，提出了一种基于改进CS-BPNN的软测量建模方法。分别采用两阶段动态发现概率法和引入附加动量与动态调整学习率来依次对CS和BPNN进行改进，仿真结果表明，和传统BPNN相比，改进CS-BPNN能更好的平衡局部搜索和全局搜索的能力，并且预测精度提高6%以上。