一种用于给水管网多目标优化的改进差分算法

莫涵 冯燕 马琪然

摘 要：针对标准差分算法无法有效处理给水管网多目标优化问题，提出一种新的算法——改进差分算法。首先，采用Pareto最优原理和非支配排序策略，建立多目标优化机制，保障算法对多个目标的协调与寻优；其次，采用精英策略取代差分算法原有的选择策略，确保每次寻优均能得到基于全局的最优个体，提高寻优效率。河内管网的优化案例表明，改进的差分算法是一种可行的、适用于给水管网多目标优化的方法。

关键词：差分算法；算法改进；给水管网；多目标优化

DOI：10. 11907/rjdk. 191287

中图分类号：TP312 文献标识码：A 文章编号：1672-7800（2019）005-0089-04

Abstract：To deal with the multiobjective optimization of the water distribution system，which can not be solved by standard difference algorithm，a new algorithm named improved difference algorithm has been proposed. Firstly， the Pareto optimal principle and non-dominated sorting strategy are adopted to establish a multiobjective optimization mechanism to ensure the coordination and optimization of the algorithm for multiple objectives.Secondly， the elite strategy is used to replace the original selection strategy of the difference algorithm to ensure that the optimal individuals based on the overall situation can be obtained for each optimization， so as to improve the efficiency of the optimization.According to the case of Hanoi pipeline network， it is proved that the improved difference algorithm proposed in this paper is a feasible method for multiobjective optimization of water distribution system.

Key Words：differential algorithm；algorithm improved；water distribution system；multiobjective optimization

0 引言

给水管网是城镇重要的基础设施，承担生活和生产用水重任，给水管网优化是否合理直接影响整个供水系统的运行效益和经济效益。长期以来，给水管网设计本身是一个难以处理的不确定性多项式问题，多数优化研究主要围绕管网经济性单一目标展开，对影响管网后期运行性能关注较少，导致现实生活中很多管网在运行期出现爆管[1-4]、漏损、局部供水不足、运行管理费用高等问题[5-6]。我国“十二五”和“十三五”规划中明确指出“要加大对供水设施的投资力度”、“增强供水管网的建设力度”[7-8]，但是如果继续延用不够完善的单目标方法设计新的给水管网，会造成大量资源浪费，这与我国建设资源节约型社会目标相违背。因此，有必要寻找一种既能实现管網经济性优化，又能实现管网可靠性优化的给水管网多目标优化方法。

标准差分算法（简称差分算法）是一种利用群体间个体差异实现启发式并行搜索的实参优化算法[9]，具有鲁棒性强、空间复杂度低、搜索能力强的特点[10-11]，常用于处理复杂、离散、非线性的优化问题。2010年，Suribabu等[12]首次将差分算法引入给水管网的优化问题研究。之后，Vasan等[13]、Zheng等[14]分别采用附加惩罚函数和参数自适应方法，对差分算法进行了改进，改进后的差分算法在处理给水管网最小经济投入的优化方面表现优异，但仍旧无法处理多个目标的优化设计问题。本文通过深入分析差分算法原理机制，结合给水管网多目标优化特点，提出一种改进差分算法并将其成功应用于河内管网优化设计，得到一系列既考虑管网经济性又兼顾管网可靠性的最优解决方案。

1 基本原理

1.1 差分算法

差分算法起源于遗传退火算法，结构与其它进化算法相似，主要由差分变异、交叉和选择环节组成。

1.1.1 差分变异

1.2 算法缺陷

以某小型环状管网为例，分别以管网成本最低、管网弹性最高及二者同时最优为优化目标，利用差分算法寻找最适合管网的管径组合方案。

（1）差分算法可快速完成给水管网的单目标寻优，但得到的优化方案并不完全符合设计要求的基本约束条件。以管网成本最低为例，差分算法找到的管径组合方案对应的管网成本极低，但将该方案包含的所有管径取出，发现部分管径为0，而实际工程中管径不允许为0。因此，该优化结果不具有实际参考意义。

（2）差分算法在处理多个目标优化时表现出明显的“惰性”，在以管网成本最低和管网弹性最高为优化目标时，算法只围绕其中一个目标展开，对另一个目标直接忽略，得到的优化结果实质上还是单目标最优，而非多目标最优。

对差分算法的运行机理进行深度剖析，发现造成上述问题的原因是差分算法缺乏判断既矛盾又竞争的多个目标优劣机制。基于此，本文对差分算法进行改进。

2 改进差分算法

2.1 Pareto最优思想

给水管网优化中，多个优化目标间的矛盾性和竞争性造成很难找到一个满足所有目标的最优解，只能通过对各目标进行权衡和折中的方式获得尽量接近全局最优解，Pareto表现的正是这种优秀的权衡思想。

目标函数空间（[Λ]）中的任意向量[u]和[v]，[u={u1，][u2，？，un}]，[v={v1，v2，？，vn}]，对于[？i∈{1，2，？，k}]满足[uivi]，并且[？j∈{1，2，？，k}]使得[ujvj]，则称[u]优于（支配）向量[v]（记作[u？v]）。

在可行性区域[Xf]中，对于[？x]不存在[a∈Xf]，使得[F（a）=（f1（a），f2（a），？，fk（a））]优于（支配）[F（x）=（f1（x），f2（x），][？，fk（x））]，即称x是[Xf]中的Pareto 最优解[18]。

2.2 非支配排序

得到Pareto最优解的关键在于判别比较对象的支配性（或非支配性）。本文采用非支配排序对种群中的所有个体对应的函数值（即适应度）进行非支配性计算，并根据计算结果进行排序，确定每个个体对应的等级情况，由此完成多个目标的判断与优选。本文采用的非支配排序过程如下：

（1）对主种群[P]中的每一个体[p]均设置两个参数[Sp]和[np]，其中[Sp]表示一个集合，包含了所有被[p]支配的个体；[np]是一个数，表示主种群[P]中支配个体[p]的个体数。

（2）对于个体[p]，初始化[Sp]和[np]，即[Sp=φ]，[np=0]。

（3）判断支配与否。将个体[p]与种群[P]中的每个个体进行比较。如果[p]支配[q]，则将[q]加到集合[Sp]里面，即[Sp=Sp？{q}]；否则，[q]支配[p]的话，则[np]值加1，即[np=np+1]。

（4）对种群[P]中的每个个体均进行支配比较，最终每个个体均对应自己的[Sp]和[np]。在所有个体中，找出[np=][0]，意味着个体[p]不被种群[P]中任何个体支配，是非支配个体。将其放到第一前沿集合（First Front，简写为[F1]），即[F1=F1？p]；再令个体[p]的解集等级为1，即[prank=1]。

（5）将[Fi]中的每个非支配个体[p]、对应[Sp]集合里的个体[q]进行支配个体数减1操作，即令[nq=nq-1]。

（6）若步骤（5）之后得到[nq=0]，说明之后的层级中无可支配个体[q]，则将个体[q]放入第2个前沿集合（[F2]），并令[qrank=prank+1]，使[F2=F2？p]。

（7）对[F2]重复步骤（4）-步骤（6）的分级操作，直到所有个體均被分级。

2.3 精英策略

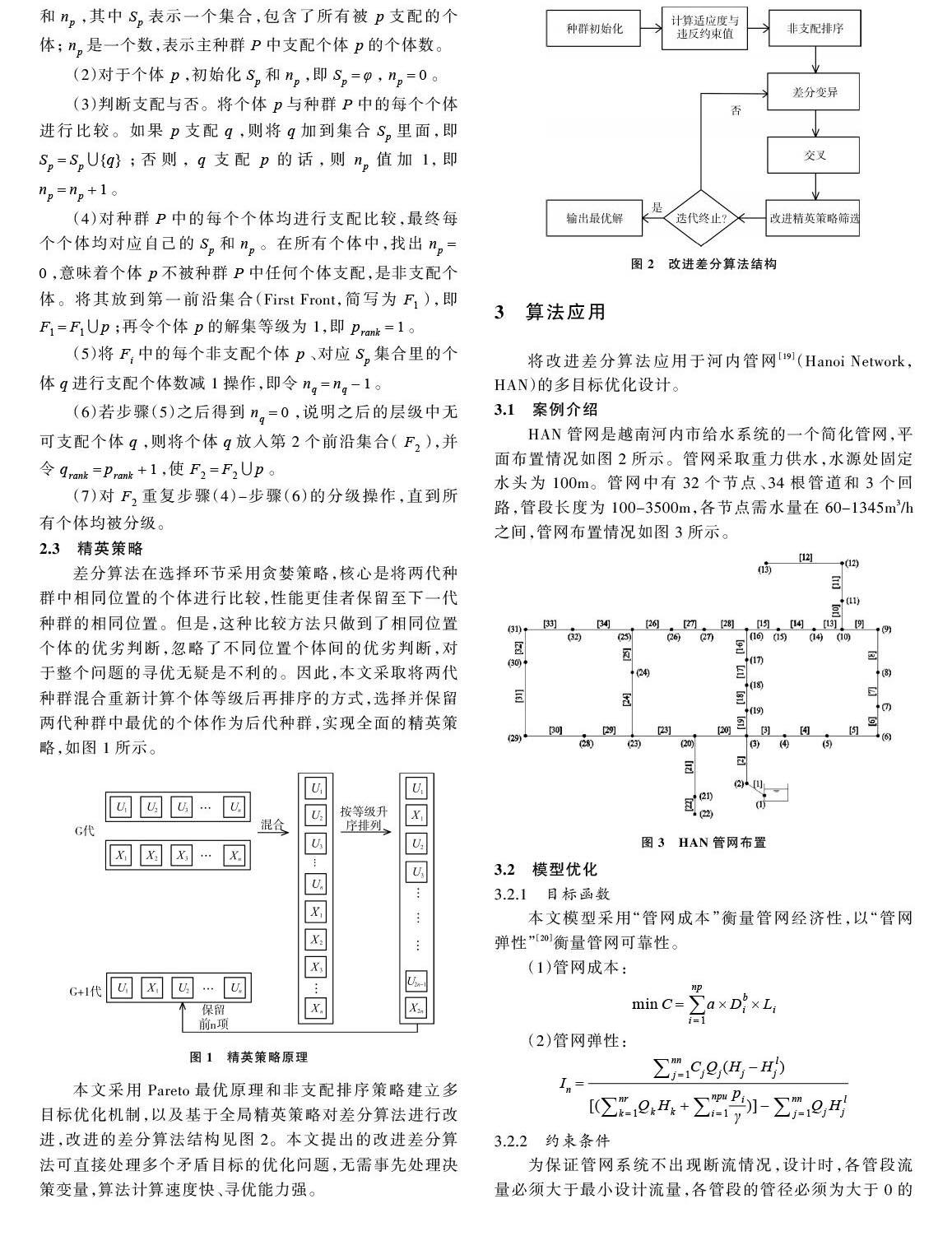
差分算法在选择环节采用贪婪策略，核心是将两代种群中相同位置的个体进行比较，性能更佳者保留至下一代种群的相同位置。但是，这种比较方法只做到了相同位置个体的优劣判断，忽略了不同位置个体间的优劣判断，对于整个问题的寻优无疑是不利的。因此，本文采取将两代种群混合重新计算个体等级后再排序的方式，选择并保留两代种群中最优的个体作为后代种群，实现全面的精英策略，如图1所示。

本文采用Pareto最优原理和非支配排序策略建立多目标优化机制，以及基于全局精英策略对差分算法进行改进，改进的差分算法结构见图2。本文提出的改进差分算法可直接处理多个矛盾目标的优化问题，无需事先处理决策变量，算法计算速度快、寻优能力强。

3 算法应用

将改进差分算法应用于河内管网[19]（Hanoi Network， HAN）的多目标优化设计。

3.1 案例介绍

HAN管网是越南河内市给水系统的一个简化管网，平面布置情况如图2所示。管网采取重力供水，水源处固定水头为100m。管网中有32个节点、34根管道和3个回路，管段长度为100-3500m，各节点需水量在60-1345m3/h之间，管网布置情况如图3所示。

3.2 模型优化

3.2.1 目标函数

本文模型采用“管网成本”衡量管网经济性，以“管网弹性”[20]衡量管网可靠性。

3.2.3 算法优化

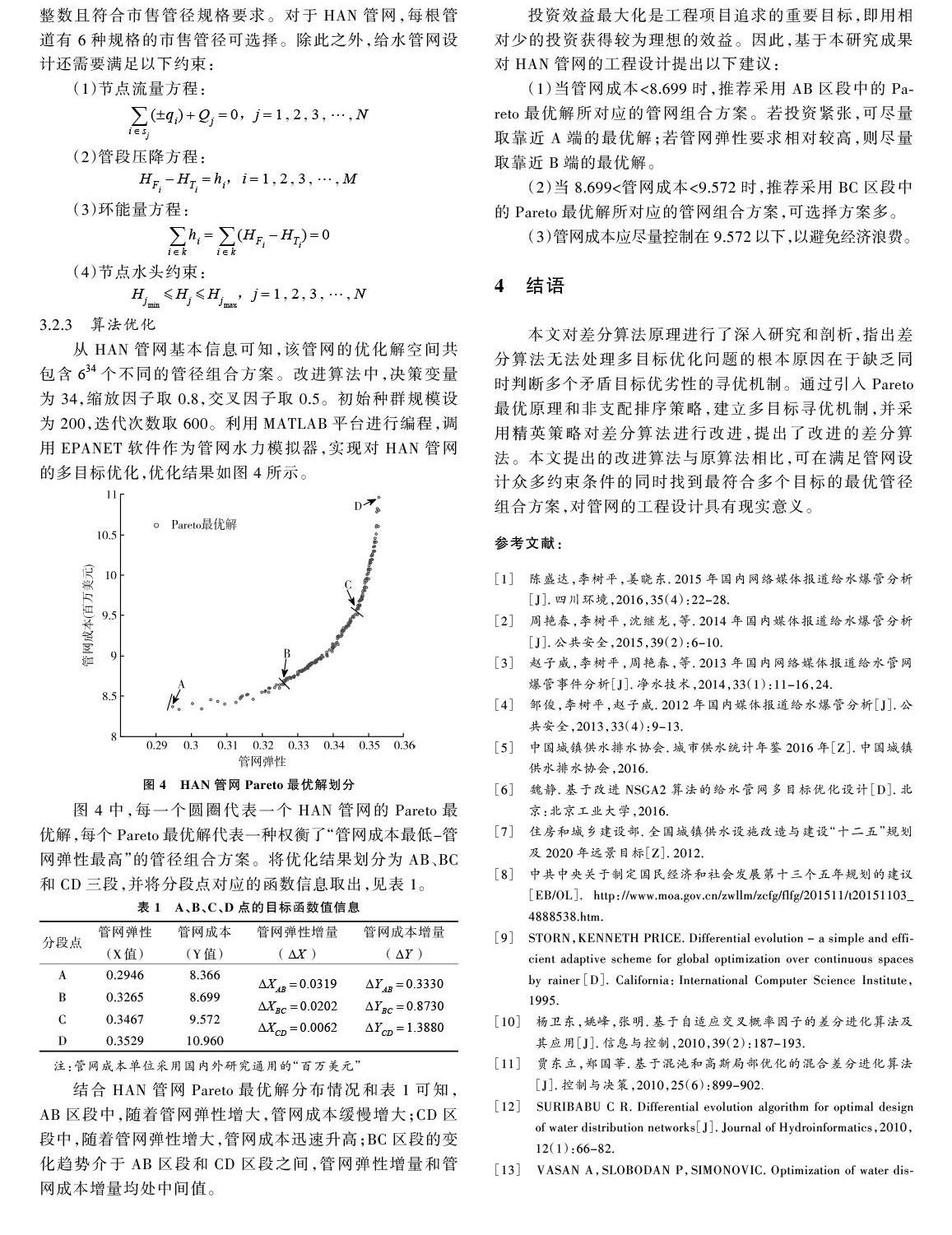
从HAN管网基本信息可知，该管网的优化解空间共包含[634]个不同的管径组合方案。改进算法中，决策变量为34，缩放因子取0.8，交叉因子取0.5。初始种群规模设为200，迭代次数取600。利用MATLAB平台进行编程，调用EPANET软件作为管网水力模拟器，实现对HAN管网的多目标优化，优化结果如图4所示。

图4中，每一个圆圈代表一个HAN管网的Pareto最优解，每个Pareto最优解代表一种权衡了“管网成本最低-管网弹性最高”的管径组合方案。将优化结果划分为AB、BC和CD三段，并将分段点对应的函数信息取出，见表1。

结合HAN管网Pareto最优解分布情况和表1可知，AB区段中，随着管网弹性增大，管网成本缓慢增大；CD区段中，随着管网弹性增大，管网成本迅速升高；BC区段的变化趋势介于AB区段和CD区段之间，管网弹性增量和管网成本增量均处中间值。

投资效益最大化是工程项目追求的重要目标，即用相对少的投资获得较为理想的效益。因此，基于本研究成果对HAN管网的工程设计提出以下建议：

（1）当管网成本<8.699时，推荐采用AB区段中的Pareto最优解所对应的管网组合方案。若投资紧张，可尽量取靠近A端的最优解；若管网弹性要求相对较高，则尽量取靠近B端的最优解。

（2）当8.699<管网成本<9.572时，推荐采用BC区段中的Pareto最优解所对应的管网组合方案，可选择方案多。

（3）管网成本应尽量控制在9.572以下，以避免经济浪费。

4 结语

本文对差分算法原理进行了深入研究和剖析，指出差分算法无法处理多目标优化问题的根本原因在于缺乏同时判断多个矛盾目标优劣性的寻优机制。通过引入Pareto最优原理和非支配排序策略，建立多目标寻优机制，并采用精英策略对差分算法进行改进，提出了改进的差分算法。本文提出的改进算法与原算法相比，可在满足管网设计众多约束条件的同时找到最符合多个目标的最优管径组合方案，对管网的工程设计具有现实意义。

参考文献：

[1] 陈盛达，李树平，姜晓东. 2015年国内网络媒体报道给水爆管分析[J]. 四川环境，2016，35（4）：22-28.

[2] 周艳春，李树平，沈继龙，等. 2014年国内媒体报道给水爆管分析[J]. 公共安全，2015，39（2）：6-10.

[3] 赵子威，李树平，周艳春，等. 2013年国内网络媒体报道给水管网爆管事件分析[J]. 净水技术，2014，33（1）：11-16，24.

[4] 邹俊，李树平，赵子威. 2012年国内媒体报道给水爆管分析[J]. 公共安全，2013，33（4）：9-13.

[5] 中国城镇供水排水协会. 城市供水统计年鉴2016年[Z]. 中国城镇供水排水协会，2016.

[6] 魏静. 基于改进NSGA2算法的给水管网多目标优化设计[D]. 北京：北京工业大学，2016.

[7] 住房和城乡建设部. 全国城镇供水设施改造与建设“十二五”规划及 2020 年远景目标[Z]. 2012.

[8] 中共中央关于制定国民经济和社会发展第十三个五年规划的建议[EB/OL]. http：//www.moa.gov.cn/zwllm/zcfg/flfg/201511/t20151103_4888538.htm.

[9] STORN，KENNETH PRICE. Differential evolution - a simple and efficient adaptive scheme for global optimization over continuous spaces by rainer[D]. California：International Computer Science Institute，1995.

[10] 杨卫东，姚峰，张明. 基于自适应交叉概率因子的差分进化算法及其应用[J]. 信息与控制，2010，39（2）：187-193.

[11] 贾东立，郑国莘. 基于混沌和高斯局部优化的混合差分进化算法[J]. 控制与决策，2010，25（6）：899-902.

[12] SURIBABU C R. Differential evolution algorithm for optimal design of water distribution networks[J]. Journal of Hydroinformatics，2010，12（1）：66-82.

[13] VASAN A，SLOBODAN P，SIMONOVIC. Optimization of water distribution network design using differential evolution[J]. Journal of water resources planning and management，2010（2）：279-287.

[14] ZHENG F F，AARON C， ZECCHIN，et al. Self-adaptive differential evolution algorithm applied to water distribution system optimization[J]. Journal of computing in civil engineering，2013（27）：148-158.

[15] BREST J，BOSKOVIC B，GREINER S，et al. Performance comparison of self-adaptive and adaptive differential evolution algorithms[J]. Soft Computing，2007，11（7）：617-629.

[16] DAS S，ABRAHAM A，CHAKRABORTY U K，et al. Differential evolution using a neighborhood based mutation operator[J]. IEEE Transactions on Evolutionary Computation，2009，13（3）：526-553.

[17] 王叢佼，王锡淮，肖建梅. 具有参数自适应机制的改进离散差分进化算法[J]. 计算机科学，2014（1）： 279-282.

[18] 王凌，何锲，金以慧. 智能约束处理技术综述[J]. 化工自动化及仪表，2008（1）：1-7.

[19] FUJIWARA O，KHANG D B. A two-phase decomposition method for optimal design of looped water distribution networks[J]. Water Resour， Res，1987，23（6）：977-982.

[20] PRASAD T D. Multiobjective genetic algorithms for design of water distribution networks[J]. Water Resour Plann Manage，2004，130（73）：73-82.

（责任编辑：杜能钢）