地形因子对偏转型滑坡-碎屑流运动参数的影响

杨海龙，樊晓一，裴向军，裴 钻

(1.成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059；2.西南科技大学土木工程与建筑学院，四川 绵阳 621010；3.工程材料与结构冲击振动四川省重点实验室，四川 绵阳 610041)

地形条件作为滑坡运动的载体，是影响滑坡运动堆积过程的决定性因素之一。因此，研究地形因子对滑坡运动参数的影响，是揭示地形条件对滑坡运动作用机制的一个重要切入点。基于滑坡大样本数据的统计分析是研究滑坡地形因子对运动参数影响的有效方法之一。樊晓一等[1]选取水平运动距离、视摩擦因数作为运动参数评价指标，分析滑面长度、滑坡坡度、坡脚角度和滑坡堆积区坡度等地形参数对不同滑坡规模的坡脚型地震滑坡运动参数的作用机制，认为研究坡脚型和偏转型滑坡运动机制不应忽略坡脚坡度差和偏转角度的作用[2]，探讨了地形因子对于不同滑坡启动机理的滑坡运动参数的影响大小[3]。以黄土滑坡大样本数据建立的滑动距离BP神经网络模型亦能较好地反映滑坡运距参数同滑坡体积参数、地形参数之间的关系[4]。一系列的室内模型试验研究表明，坡脚角度是碎屑流最大运动距离[5]、视摩擦系数[6]和前缘速度[7]的显著性影响因子；坡脚对碎屑流前缘的阻止作用显著，坡度越大滑坡的能量消耗也就越大[8]。对不同下垫面条件下的滑坡运动数值模拟表明，下垫面摩擦系数[9]、地形起伏度[10]、滑面粗糙度[11]等地形参数是影响滑坡运动参数的主要因素，表现为对滑坡运动距离、前缘速度的影响。因此，为了减小运动参数预测的离散性，在预测模型中应充分考虑各地形因子对滑坡运动参数的影响，以提高预测模型的可靠性。

已有研究重点关注地形因子对运动参数的影响大小，缺乏运动参数与主控地形因子间关系模型的描述。因此，本文选取沟谷地形中常见的一类滑坡运动形式即偏转型滑坡为研究对象，对偏转型滑坡-碎屑流的场地条件进行概化、分类并提取主要地形参数，借助数值模拟手段进行不同地形因子组合条件下的滑坡-碎屑流模拟，揭示主要地形因子对滑坡运动参数的影响规律，为沟谷偏转型滑坡-碎屑流运动参数模型的建立提供参考。

1 沟谷偏转型滑坡地形特征

偏转型滑坡-碎屑流是沟谷地形中常见的一种滑坡运动形式。沟谷地形对滑坡运动产生约束作用，从而导致滑坡运动方向发生偏转，并产生相对较远的运动距离。此类滑坡的显著地形特征表现为存在的两个典型的地形突变点，选取典型沟谷偏转型滑坡碎屑流实例进行说明(图1)。

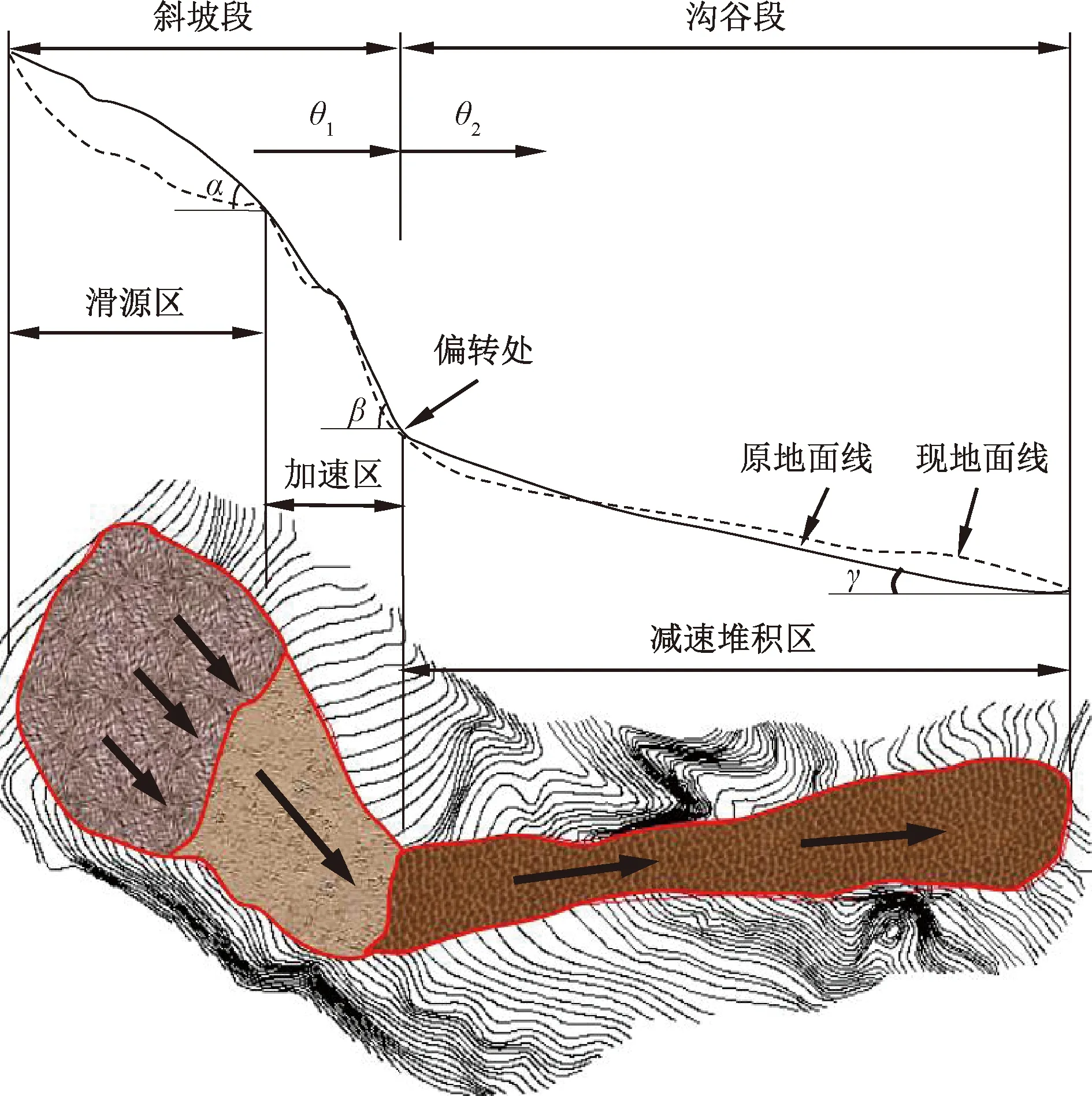
图1 典型偏转型滑坡碎屑流场地特征Fig.1 Site condition of landslide-debris avalanchesof the typical turning-type

地形突变点1位于坡面，是滑源区与加速区的分界点；地形突变点2位于沟谷坡脚处，是斜坡加速区与沟谷堆积区的分界点以及滑坡运动方向的分界点。因此，主要地形参数包括为滑源区坡度(α)、斜坡坡度(β)和沟谷坡度(γ)和偏转角度(θ)。借鉴相关文献[12-13]中有关地形条件概化分类的方法，根据坡面特征可进一步将偏转型滑坡地形划分为凹面偏转型、凸面偏转型和坡脚偏转型(表1)。

表1 偏转型滑坡场地分类Table 1 Types of site condition of landslide of the turning-type

2 研究方案

2.1 研究方法

由于模拟对象不考虑运动过程中的解体破碎效应，根据碎屑流颗粒的结构特征和力学行为，采用离散元素法模拟滑坡碎屑流在运动过程中的力学行为。碎屑流颗粒间的接触力学模型是离散元素法求解颗粒运动状态和受力的关键[14]。模拟对象为无黏性的岩石碎屑流颗粒，颗粒表面黏附力小，具有散粒物料特性。因此，本文中采用Hertz-Mindlin(no-slip)接触模型。

2.2 模拟材料与参数选取

选用文[5]中的岩土体S5作为本文偏转型滑坡碎屑流的模拟材料，颗粒级配如图2所示。由于颗粒模型与真实颗粒在形状、表面粗糙度等方面仍存在差异，若直接引入真实颗粒的相关参数进行模拟，则不能准确反映碎屑流的真实运动状态，因此需要对模拟参数进行标定[15]。

图2 碎屑流颗粒级配Fig.2 Particle gradation of debris flow

利用DEM模拟碎屑流的运动过程需要的物理参数见表2，其中泊松比δ、密度ρ、剪切模量G、弹性恢复系数е均可通过土工实验获得，颗粒与滑槽间的ξ2取值宜与颗粒间的ξ2相同，颗粒与滑槽间的ξ1也可由试验确定。因此，只需要对碎屑流颗粒间的ξ1、ξ2进行标定。

参考文[15]中对颗粒间ξ1、ξ2的标定方法，采用堆积法和内部坍塌法进行休止角仿真试验，利用MATLAB图像处理技术获取堆积角正切值τ，建立自变量为ξ1、ξ2，因变量为τ的回归方程：

最后代入岩土体的真实休止角求解ξ1、ξ2即完成参数标定(表2)。

2.3 数值模型

根据偏转型滑坡碎屑流地形特征构建滑槽模型，滑槽模型由料箱、上部滑槽和下部滑槽三部分组成，建模过程在Rhino中完成(图3)。

表2 模拟参数取值Table 2 Values of simulation parameters

图3 滑槽模型示意图Fig.3 Schematic diagram of the chute mode

上部滑槽用于模拟碎屑流在坡面上的加速运动，高度固定为1.25 m；下部滑槽用于模拟碎屑流在沟谷中受偏转作用后的运动堆积过程，滑槽模型宽度和两侧挡板高度均为0.5 m。滑源区坡度、斜坡坡度和沟谷坡度和偏转角度可根据模拟方案进行调整。

碎屑流颗粒模型根据颗粒级配曲线生成，颗粒形状采用圆形颗粒组合成不规则的岩土体颗粒。在滑源区的堆积形态为三棱柱体，体积方量为0.025 m3，约60 000个碎屑流颗粒(图4a)。为了加速碎屑流颗粒在指定区域生成，赋予颗粒一定的初始速度。由于颗粒具有初始速度，当所有颗粒运动到指定区域堆积后在一段时间内不会静止，为了加速颗粒静止可以适当提高颗粒间的摩擦系数，减小碰撞恢复系数。当颗粒最大速度小于0.05 m/s时，可以认为颗粒已经达到静止状态(图4b)。

图4 碎屑流模型示意图Fig.4 Schematic diagram of debris flow

2.4 模拟方案

滑源区坡度(α)、斜坡坡度(β)、沟谷坡度(γ)和偏转角度(θ)共同决定了沟谷偏转型滑坡的地形条件。由于滑源区坡度与斜坡坡度之间的关系决定了坡面地形特征，是进一步划分偏转型滑坡类型的依据。因此设定滑源区坡度为定值，主要考虑斜坡坡度、沟谷坡度和偏转角度的变化。3个地形参数分别取3种水平，共进行27组仿真模拟。其中为了减小误差，每组模拟重复3次，取3次模拟结果的平均值作为该组最后的模拟结果(表3)。

2.5 运动参数指标选取

选取合理的运动参数作为评价指标是地形因子对偏转型滑坡运动特征影响分析的关键。视摩擦系数(f)

表示滑体在运动路径上克服摩擦力所做的功，在一定程度上反映了滑坡运动路径上地形条件对滑坡运动的阻止效应。前缘速度恢复系数(k)即坡脚偏转前后的滑坡前缘速度的比值，反映坡脚偏转作用对碎屑流前缘的阻止效应。此二者均为偏转型滑坡重要的运动参数，因此本文选取其作为滑坡运动参数的评价指标。

表3 参数变量及取值Table 3 Parameter variables and values

2.6 模拟结果

偏转型滑坡碎屑流在不同地形参数组合地形条件下的运动过程如图5所示(以β=55°、γ=5°、θ=20°为例)，滑坡运动参数(f、k)的模拟结果见表4。

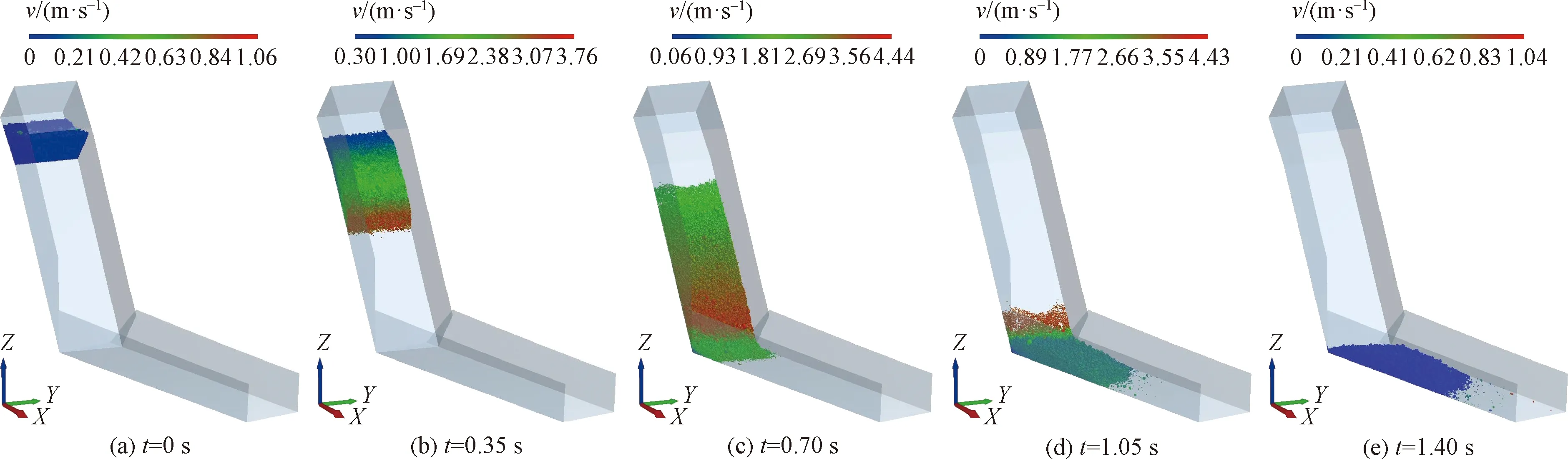
图5 偏转型滑坡碎屑流的动过程Fig.5 Movement process of landslide-debris flow of the turning-type

表4 运动参数的模拟结果Table 4 Simulation results of motion parameters

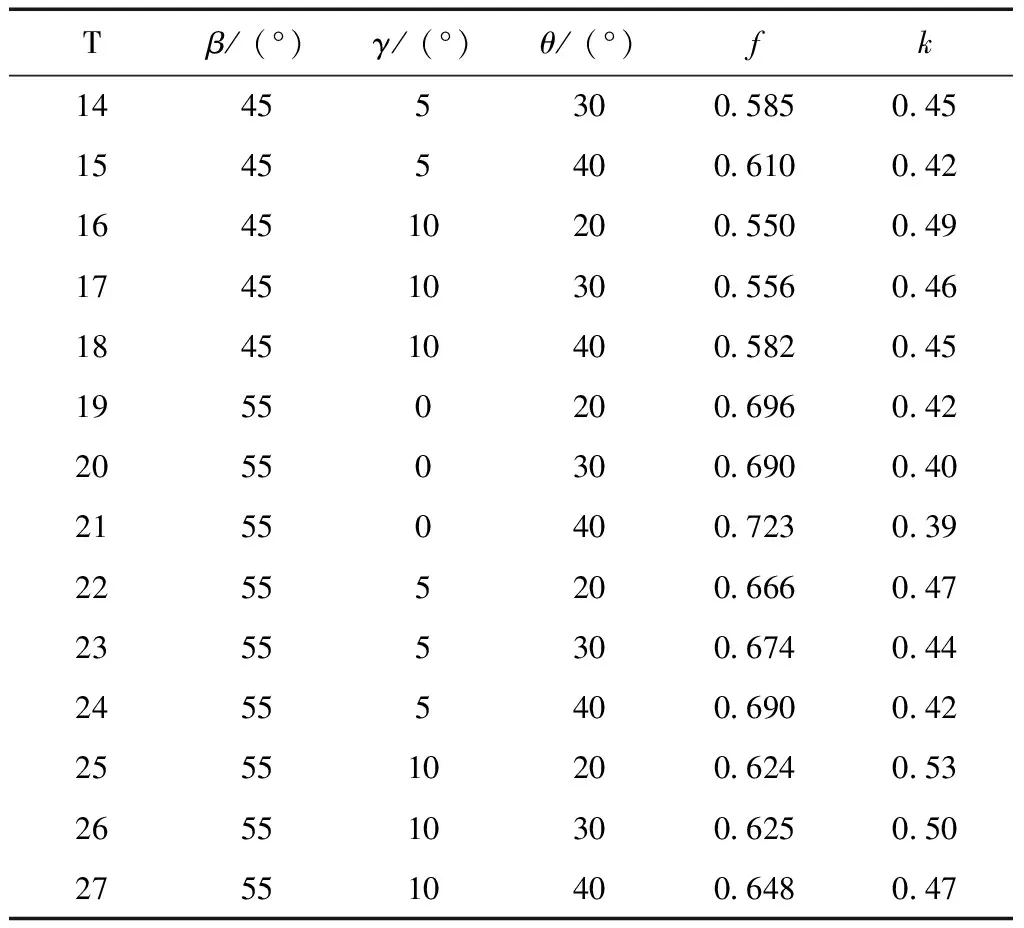
续表4

3 偏转型滑坡运动特征分析

地形参数对视摩擦系数(f)、前缘速度恢复系数(k)的影响如图6所示。视摩擦系数随斜坡坡度和偏转角度的增大而增大，随沟谷坡度的增大而减小；前缘速度恢复系数随斜坡坡度的增大先减小后增大，随偏转角度的增大而减小，随堆积区坡度的增大而增大。上述分析表明，偏转型滑坡的运动受斜坡坡度、沟谷坡度、偏转角度的影响。但是地形参数对偏转型滑坡运动的影响大小以及地形因子对运动参数的作用机制尚不清楚。

3.1 地形因子对视摩擦系数的影响分析

3.1.1地形因子敏感度分析

采用正交分析法[5,16]分析地形因子(β、γ、θ)对摩擦系数的影响(表5)，分析结果表明：在不同斜坡坡度条件下，偏转角度对视摩擦系数的影响小于沟谷坡度；在不同沟谷坡度条件下，偏转角度对视摩擦系数的影响也小于斜坡坡度；在不同偏转角度条件下，斜坡坡度对视摩擦系数的影响大于沟谷坡度。

各地形因子在不同水平下，视摩擦系数极差平均值R2=0.008，运动参数f平均值f2=0.587，相对误差为1.43%，试验误差较小，试验结果可靠，可以进行极差分析。视摩擦系数的极差分析结果见表6，Ii、IIi、IIIi表示在不同因素水平下视摩擦系数的平均值，Ri

为极差。当斜坡坡度处于不同水平时，视摩擦系数的波动程度显著大于沟谷坡度和偏转角度(图7)，即斜坡坡度对视摩擦系数的影响最大，沟谷坡度、偏转角度次之。

极差分析初步判定了各地形因子对偏转型滑坡运动参数的重要程度，为了避免由于试验误差引起的数据波动所造成的误判，采用方差分析法进一步对视摩擦系数f影响因子的重要程度进行分析(表7)。分析结果表明：斜坡坡度对视摩擦系数的影响非常显著，是决定性因素；沟谷坡度、偏转角度对视摩擦系数的影响不显著，为非决定性因素。综上，沟谷坡度、偏转角度对视摩擦系数的影响均小于斜坡坡度。

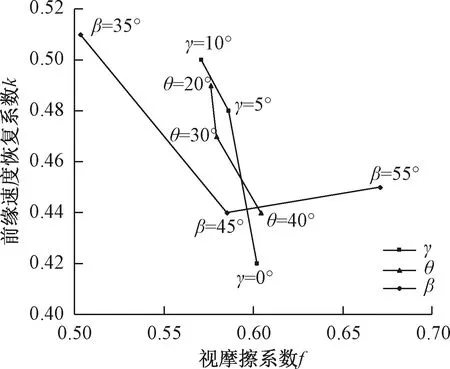
图6 不同因素水平下运动参数的变化趋势Fig.6 Changes of motion parameterswith different factors

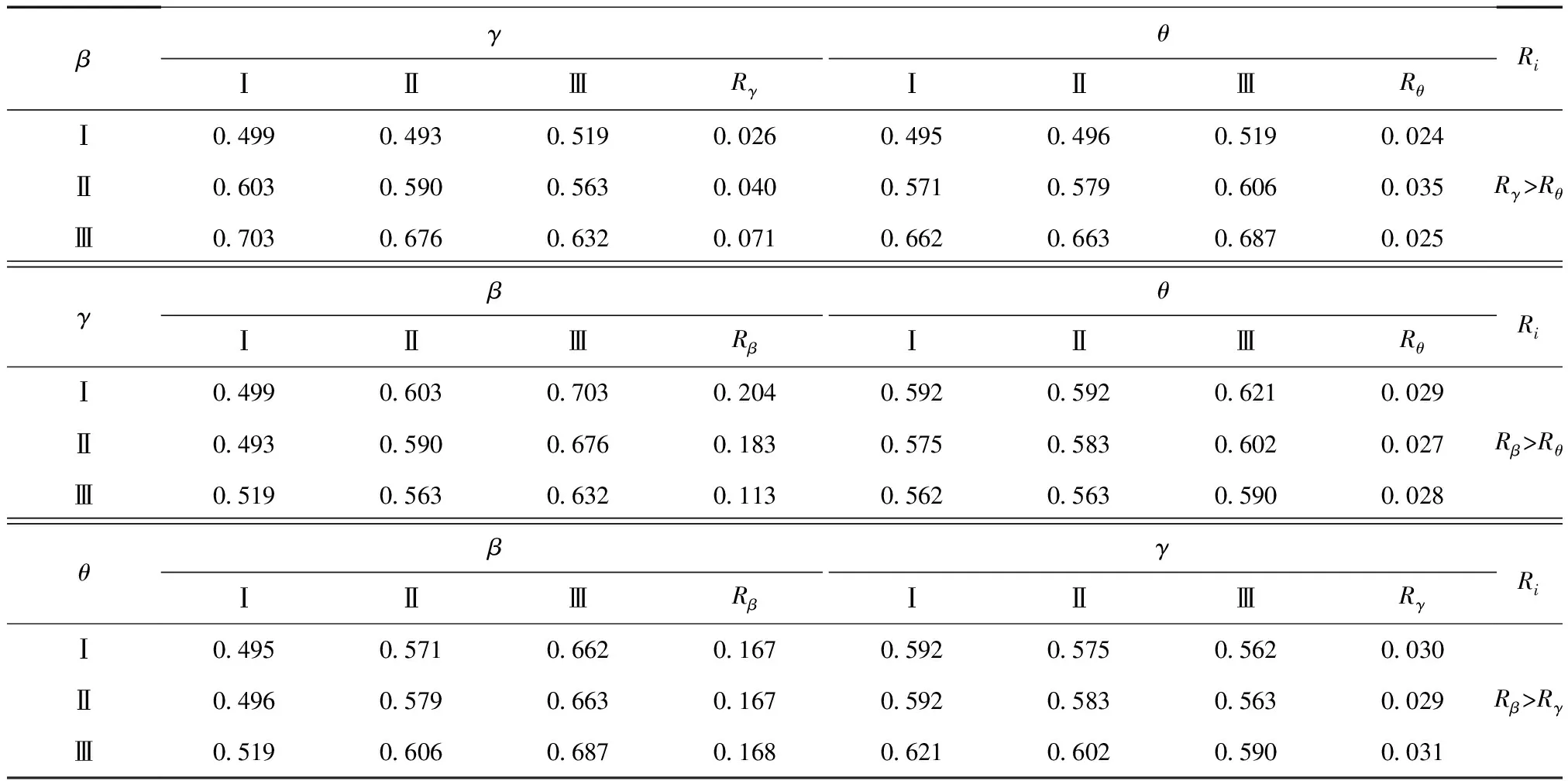
表5 视摩擦系数f正交分析结果Table 5 Orthogonal analysis of apparent coefficient of friction

表6 视摩擦系数极差分析结果Table 6 Range analysis of apparent coefficient of friction

图7 视摩擦系数与各影响因素的关系Fig.7 Relationship between apparent coefficientof friction and factors

nf0.05f0.01SASEF显著性β23.405.610.1260.01695.3∗∗γ23.405.610.0040.1370.36-θ23.405.610.0040.1370.37-

注：** 表示非常显著；-表示不显著

3.1.2视摩擦系数与显著性因子间关系分析

方差分析表明，影响沟谷偏转型滑坡-碎屑流视摩擦系数(f)的显著性地形因子是斜坡坡度(β)。采用回归分析法，建立视摩擦系数与加速区坡度之间的函数关系，定量描述视摩擦系数与显著性地形因子之间的关系。将偏转型滑坡碎屑流运动参数与显著性地形因子间的非线性模型描述为：

①不同年龄医护工作者职业认同水平具有差异性。其中年龄＞50岁的医护工作者职业认同程度高于其他年龄医护工作者，≤30岁的医护工作者职业认同程度最低，随着年龄增加医护工作者职业认同程度提高。

f=η0+η1tanβ+η2tan2β

(1)

式中：η0——常数；

η1——β的回归系数。

为了保证回归模型的合理性，对27组模拟数据进行残差分析，发现异常点5处并剔除(图8)；最后对剩余22组数据进行回归分析，可以得到非线性回归方程：

f=0.27+0.38tanβ-0.06tan2β

(2)

对回归结果进行检验：相关系数R=0.95，即观测值与回归方程拟合程度高，临界值F=196.12>>F0.99(1，20)=8.02>F0.95(1，20)=4.35，回归效果非常显著；表明偏转型滑坡碎屑流的视摩擦系数与斜坡坡度之间具有较强的非线性关系，可以用二次函数进行描述(图9)。

图8 视摩擦系数残差分析Fig.8 Residual analysis of apparent coefficient of friction

图9 视摩擦系数与主要影响因子间的关系Fig.9 Relationship between the apparent coefficient offriction and the main influence factor

3.2 地形因子对前缘速度恢复系数的影响分析

3.2.1地形因子敏感度分析

地形因子(β、γ、θ)对前缘速度恢复系数k影响的正交分析结果见表8，结果表明：在不同斜坡坡度条件下，偏转角度对前缘速度恢复系数的影响小于沟谷坡度；在不同沟谷坡度条件下，偏转角度对前缘速度恢复系数的影响也小于斜坡坡度；在不同偏转角度条件下，斜坡坡度对前缘速度恢复系数的影响小于沟谷坡度。

各地形因子在不同水平下，前缘速度恢复系数的极差平均值R2=0.007，平均值f2=0.467，相对误差为1.59%，表明试验误差较小，试验结果可靠，可以进行极差分析。前缘速度恢复系数的极差分析结果见表9，Ii、IIi、IIIi表示在不同因素水平下前缘速度恢复系数的平均值，Ri为极差。

当沟谷坡度处于不同水平时，前缘速度恢复系数k的波动程度略大于斜坡坡度，但均大于偏转角度(图10)，即沟谷坡度对前缘速度恢复系数的影响最大，斜坡坡度次之，偏转角度最小。

表8 前缘速度恢复系数正交分析结果Table 8 Orthogonal analysis of the restitution coefficient of mass-front velocity

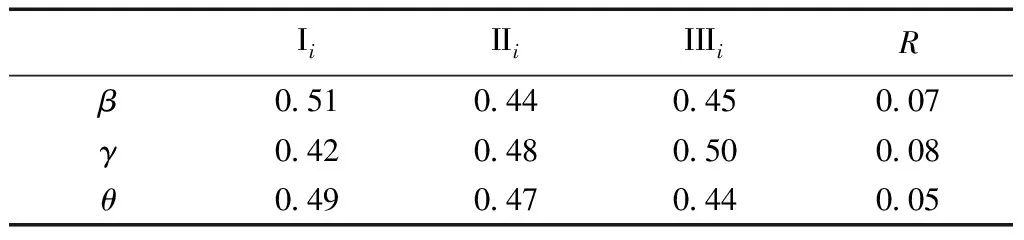
表9 前缘速度恢复系数极差分析Table 9 Range analysis of the restitution coefficientof mass-front velocity

图10 前缘速度恢复系数与各影响因素的关系Fig.10 Relationship between the restitution coefficientof mass-front velocity and influence factors

nf0.05f0.01SASEF显著性β23.405.610.0220.0515.10∗γ23.405.610.0310.0428.82∗∗θ23.405.610.0110.0622.19-

注：** 表示非常显著；*表示显著；-表示不显著

3.2.2前缘速度恢复系数与显著性因子关系分析

方差分析表明，影响沟谷-偏转型滑坡碎屑流前缘速度恢复系数(k)的显著性地形因子是斜坡坡度(β)、沟谷坡度(γ)。采用回归分析法，建立前缘速度恢复系数与斜坡坡度、沟谷坡度之间的函数关系，定量描述前缘速度恢复系数与显著性地形因子之间的关系。因此，将前缘速度恢复系数与显著性地形因子β、γ间的非线性模型描述为：

k=η0+η1tanβ+η2tanγ+η3tanβtanγ+

η4tan2β+η5tan2γ

(3)

式中：η0——常数；

η1、η2、η3、η4、η5——tanβ、tanγ的回归系数。

为了保证回归模型的合理性，对27组模拟数据进行残差分析，发现异常点2处并剔除(图11)；最后对剩余25组数据进行回归分析，可以得到非线性回归方程：

k=0.28tan2β-0.23tan2γ-0.68tanβ+0.31tanγ+0.14tanβtanγ+0.80

(4)

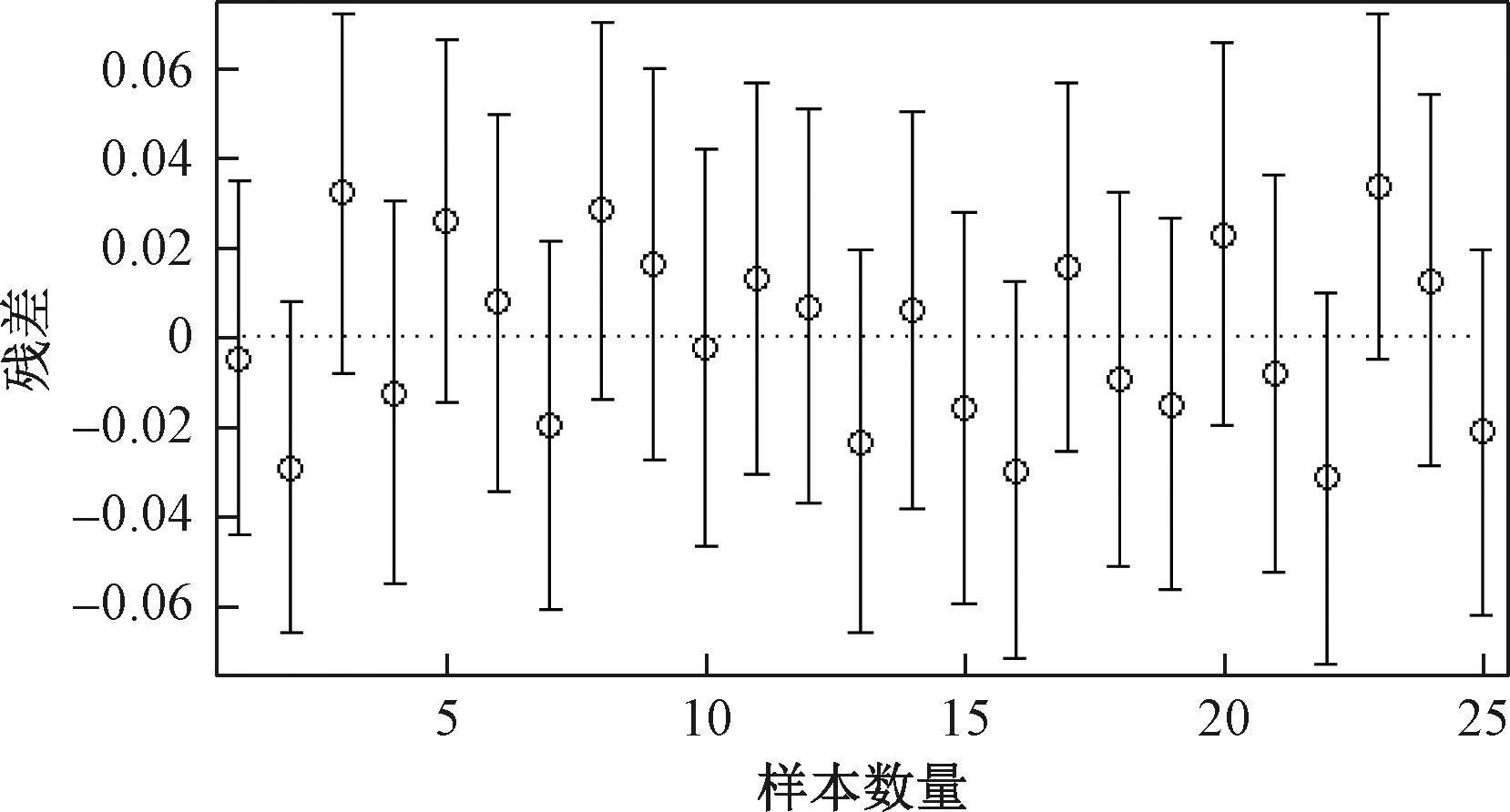
图11 前缘速度恢复系数残差分析Fig.11 Residual analysis of the restitution coefficientof front velocity

对回归结果进行检验：相关系数R2=0.80，即观测值与回归方程拟合程度高，临界值F=15.30>F0.99(2，22)=5.72>F0.95(2，22)=3.44，回归效果非常显著；表明偏转型滑坡-碎屑流的前缘速度恢复系数与斜坡坡度和沟谷坡度间存在较强的非线性关系，可以用二次型函数描述(图12)。

图12 前缘速度恢复系数与主要影响因子间的关系Fig.12 Relationship between the restitution coefficientof mass-front velocity and the main influence factors

4 结论

(1)沟谷偏转型滑坡-碎屑流的显著地形特征表现为运动区域之间存在两个重要的地形分界点，主要地形参数为滑源区坡度、斜坡坡度、沟谷坡度和偏转角度，根据坡面地形特征可将沟谷偏转型滑坡进一步分为坡脚偏转型、凹面偏转型和陡坡偏转型。

(2)沟谷偏转型滑坡的视摩擦系数、前缘速度恢复系数均主要受地形起伏的影响。斜坡坡度对视摩擦系数的影响最大，沟谷坡度次之，偏转角度最小；斜坡坡度、沟谷坡度对前缘速度恢复系数的影响远大于偏转角度的影响。因此，斜坡坡度是视摩擦系数的显著性因素；斜坡坡度、沟谷坡度是前缘速度恢复系数的显著性因素。

(3)沟谷偏转型滑坡运动参数与主要影响因子之间的非线性关系非常显著。视摩擦系数与斜坡坡度之间的非线性关系可用二次函数描述；前缘速度恢复系数与斜坡坡度、沟谷坡度间的非线性关系，可用二次型函数描述。