含分数阶的灰色模型及其在地基沉降预测中的应用
2019-05-24赖文杰齐昌广郑金辉王新泉左殿军
赖文杰,齐昌广,郑金辉,王新泉,左殿军
(1.宁波大学建筑工程与环境学院,浙江 宁波 315211;2. 浙江大学城市学院土木工程系,浙江 杭州 310015;3. 交通运输部天津水运工程科学研究院岩土工程研究中心,天津 300456; 4. 河海大学土木与交通学院,江苏 南京 210098)
路基实测数据沉降预测方法是交通土建工程界研究的热点,同时也是软基沉降控制计算方法理论研究的一大难题。这是由于软基实际固结规律的复杂形式难于用一般数学曲线拟合所造成的。为了更好地通过实测数据预测路基沉降发展规律,工程界对基于实测数据的沉降预测方法进行了广泛的研究,其中具有代表性的有:双曲线法、三点法、指数函数法、Asaoka法、灰色模型预测法等。通过将上述方法的预测结果和实测沉降数据对比发现,预测方法计算结果仍与实际值有较大的误差,故需对传统预测模型及计算方法做进一步改进。
目前国内对沉降预测模型及计算方法的改进研究主要有:甘友文等[1]对传统对双曲线预测模型进行改进,提出精度更高的修正的双曲线模型。王志亮等[2]基于抛物线插值法和直线最小二乘法,对Asaoka法中时间间隔取值Δt进行研究,该方法成功应用于多级荷载路堤工程中的沉降预测。肖治宇[3]将自适应神经模糊推理系统(ANFIS)应用于软基沉降预测,提出ANFIS软土地基沉降预测模型。该模型克服了局部极小值的缺点,预测精度高于传统的生长曲线预测模型。唐利民[4]指出最小二乘法的病态性会导致沉降预测模型参数求解失败,可通过正则化无偏估计处理参数来提高预测精度。朱志铎等[5]基于成长型曲线建立软基全过程沉降预测的Logistic模型,确定模型参数及其对不同阶段的地基沉降影响。曹文贵等[6]对单项预测模型沉降的计算和实测值的误差描述方法进行改进,拟合出新型目标误差函数,从而获得简单实用的工后沉降预测方法。复杂工况下的沉降规律并不明显,为了能够更准确预测沉降,众多学者采用灰色理论来预测地基沉降。如刘国华等[7]将基于单变量的灰色预测模型推广至多变量的灰色预测模型。李洪然等[8]采用参数累计法代替最小二乘法对传统GM(1,1)地面沉降模型进行修正,构建了参数估计的灰色沉降预测模型。此外,苗雨等[9]、李篷等[10]也对灰色理论预测沉降提出相关计算模型,并给出了误差性分析。虽然上述基于灰色理论建立的沉降计算模型具有一定的应用价值,但求解的微分方程均为整数阶,即预测模型存在不连续的问题,局限性较大。

本文以灰色预测模型为研究对象,把模型中的一阶微分代换为分数阶微分,提出一种基于分数阶的灰色预测模型。与传统灰色预测模型相比,增加了分数阶阶次的识别,从而增大参数识别的难度。为此,笔者基于分数阶系统模型,建立了含分数阶的灰色模型,结合工程实例验证该模型的合理性,并计算了分数阶灰色预测模型误差。
1 分数阶系统模型
分数阶目前存在三种定义,本文采用Caputo微积分定义,函数y(t)的α阶微分可表示为:
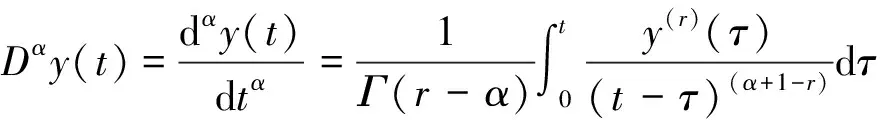
(1)
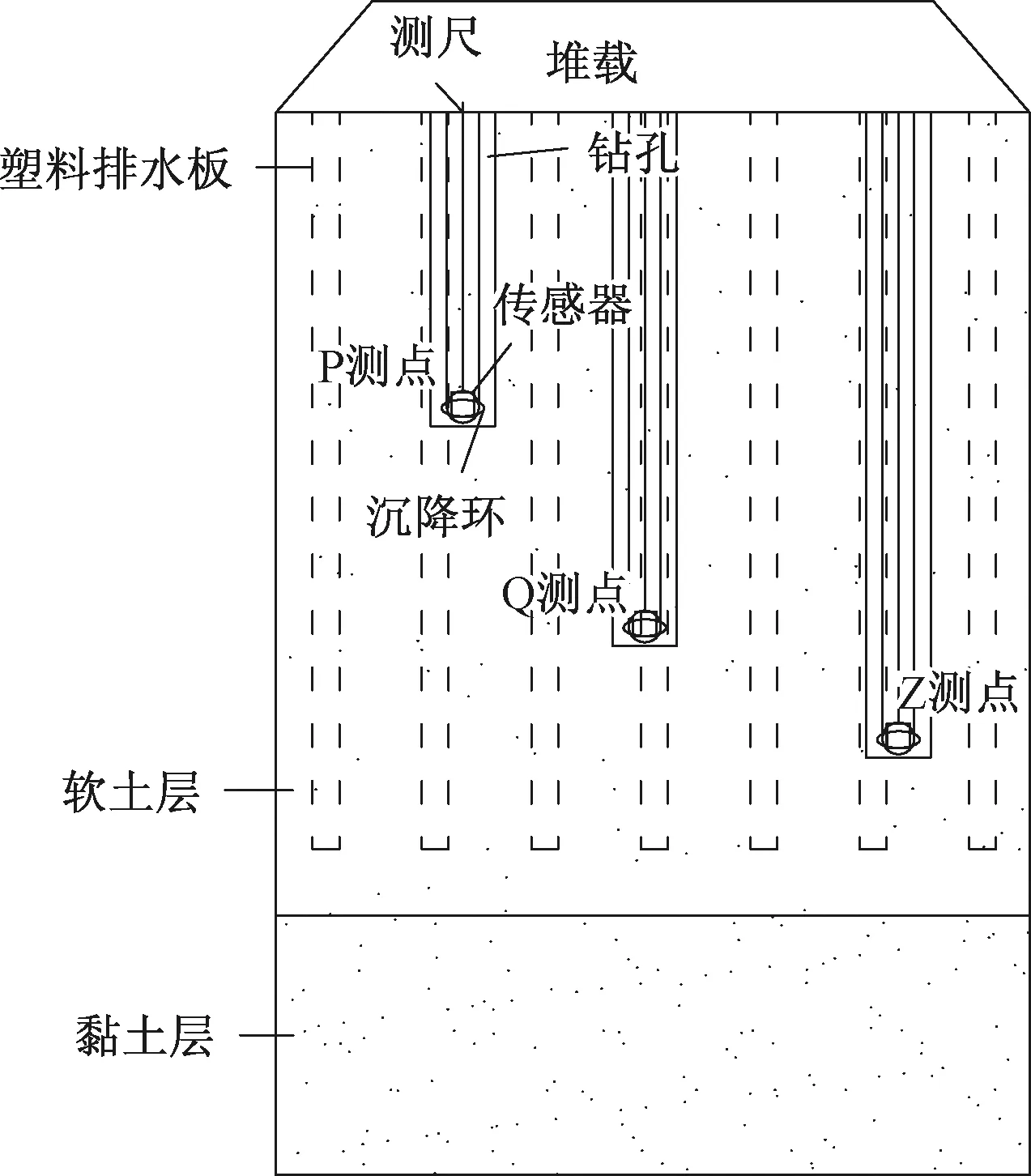
r-1<α 式中:r——正整数; α——一个分数; Γ()——Gamma函数。 (2) 其Laplace变换可表示为: (3) 本文中,考虑的为零初始条件,此时,Laplace变换为: L[Dαy(t)]=sαY(s) (4) 有关sα的计算,通常采用整数阶积分进行近似处理,本文采用相位前置式滤波器的方式来模拟sα的输出结果。假设拟合频率段为(ωb,ωh),则可构造如下滤波器的传递函数,为: (5) 式中:2N+1——所选择的滤波器阶次。 式(5)也可表示为状态方程的形式: w=CIzI(t)(6) 式中:zI(t)——N+1维状态矢量。 CI=[0 … 0 1] 式(6)可转换为: w=CzI(t) (7) 设原始时间序列为: y(0)=[y(0)(1)y(0)(2) …y(0)(n)] 其一次累加生成序列为: y=[y(1)y(2) …y(n)] 则灰色模型可表示为: (8) 式(8)中的待定常数b1、b2由下式确定: (9) 从式(8)可以看出,灰色模型是无输入的常微分方程,这里对其做两个方面的变动:其一是增加输入项u;其二是变常微分方程为分数阶微分方程,即: (10) 为保持原灰色模型的特点,此处,输入项u可采用单位阶跃函数,即: (11) 对式(10)两边进行Laplace变换,可得系统的传递函数为: (12) 若定义z(t)的频域表示为: (13) 则输出变量y(t)可表示为: Dαz(t)=-b1z(t)+u(t) y(t)=b2z(t) (14) 上式可等效地写为: y(t)=b2zN+1(t) (15) (16) 需要说明两点:其一,含分数阶的模型识别,需要系统输入,按式(11)输入才能得到正确结果;其二,与常规的灰色模型识别方法相比,虽然只是增加了一个参数α(或者是中间参数δ和η),但就是由于参数α的出现,使得识别难度大大增加,在获得式(16)之后,方可使得识别变得可行。具体识别算法可采用常规的识别算法即可,如Marquardt算法[16]等。 以浙江省某高速公路K1049+678断面为例,该段地基富含软土,压缩性较大。通过在地基上打入塑料排水板将土体内的水分排出,并在断面上选择P、Q、Z三个点进行沉降监测(图1)。工程自2016年3月开工,沉降监测频率为30 d/次,并于2017年6月22日截止。利用传统的双曲线沉降预测模型及本文提出的含分数阶灰色理论预测模型对该断面的沉降数据进行计算,并对计算结果进行验证分析。沉降观测点原始数据见表1。 以2016年3月至10月的数据作为原始数据进行建模预测,预测2016年11月至2017年6月的沉降,并与实测值进行对比。 采用本文所提出的模型(即式(10)),在采用分数阶微分滤波器近似时,考虑到高速公路的特点,选择的拟合频率段为(0.001 1000)rad/s,N=4,即滤波器的阶次为9。参数估计分别为: α=1.14;b1=0.135;b2=1.200 V(s)=2.63·s10+1398·s9+1.316×105·s8+2.573×106·s7+1.075·107·s6+9.652×106·s5+1.864×106·s4+7.692·104·s3+658.7·s2+s W(s)=s9+658.7·s8+7.692×104·s7+1.864×106·s6+9.652×106·s5+1.075×107·s4+2.573×106·s3+1.316×105·s2+1398·s+2.63 图1 测点布置简图Fig.1 Schematic diagram of the measuring points 表1 沉降观测原始数据 通过二阶范数进行误差分析,定义式如下: (17) 式中:y——实测累加数据; 传统双曲线沉降预测模型的计算表达式[17]如下: (18) 式中:S0——时间t0时的累积沉降量; t0——时间零点; St——时间t时的累积沉降量; 根据图解法得到: 观测点P:α=0.7779,β=0.0553 观测点Q:α=0.9071,β=0.0426 观测点Z:α=0.8057,β=0.0273 将α,β代入式(18)中,即可得到传统双曲线沉降预测模型。 采用灰色预测模型时(即式(8)),可由式(9)估计其参数,分别为: 观测点P:b1=0.0729;b2=127.0539 观测点Q:b1=0.0759;b2=116.4983 观测点Z:b1=0.0591;b2=131.0533 根据计算得到的参数,代入式(8)可计算出整数阶预测模型。 根据式(17),双曲线预测模型计算的P,Q,Z误差分别为282,139,225,整数阶模型的误差为186,202,93。本文提出含分数阶灰色模型方法的误差分别为116,63,53,可见本文提出含分数阶灰色预测模型较传统双曲线和整数阶预测模型计算结果更优。 将实测结果和本文含分数阶灰色理论预测模型计算结果、传统双曲线预测模型、整数阶汇于图2中,相比较可以看出,本文提出含分数阶灰色理论沉降计算方法能得到更好地预测结果。 图2 实测结果与预测结果的比较Fig.2 Comparison of the measured results andpredicted results at points (1)传统的灰色模型是无输入的常微分方程,本文对其进行两方面的改进:其一是增加输入项u;其二是变常微分方程为分数阶微分方程。 (2)结合工程实例对分数阶灰色模型、整数阶灰色模型及双曲线模型进行误差计算,本文建立的含分数阶灰色理论预测结果与工程实测结果之间的误差较整数阶灰色理论沉降预测模型、双曲线预测模型的精度更高,与实测结果拟合更好。



2 含分数阶的灰色模型






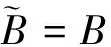
3 预测模型在沉降预测中的应用




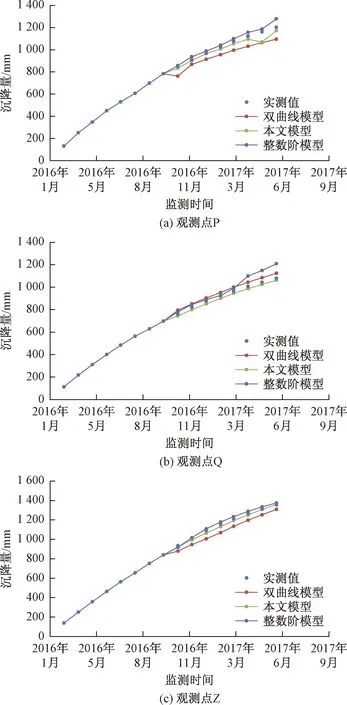
4 结论
