多段曲线拟合弹齿式枝条捡拾参数反求法求解

李 辉，杨爱茜，李建平，王利源，刘俊峰，杨 欣

(1.河北农业大学 机电学院，河北 保定 071000；2.衡水学院，河北 衡水 053000)

0 引言

长期以来，我国水果种植保持着“非集约式”管理模式。随着机械化水平的提高，其技术繁杂、耗时费力、生产成本高的弊端逐渐显露出来。近年来，随着我国土地大面积集中流转政策的实施，乔砧栽培的老龄化果园将被矮砧集约栽培种植模式逐渐替代。矮砧集约栽培种植模式具有农业机械化水平高、生产成本低、适合大规模果园管理的优势。

针对矮砧集约栽培种植现代果园中每年剪枝后产生的大量枝条的现象，采取粉碎处理直接还田的措施，不仅增加土壤中有机质含量、增强土壤保水保肥能力的效果，且可以达到减少化肥施用量、保护环境的目的。由于这种栽培种植模式果园行间距小，大型枝条粉碎设备无法进入果园内移动作业，因此需要一种适合果园行间高效移动式处理枝条的设备。根据现代果园修剪的枝条具有直径小、大树叉少、修剪后枝条整体大部分紧贴地表等特点，研究了拖拉机悬挂式枝条处理设备的关键性部件—弹齿滚筒式枝条捡拾器[1-3]。捡拾器轴向弹齿数量多，具有轴向排列密度高、漏枝率低、整体质量轻及耗能低的优点。

1 枝条捡拾器数学模型

如图1所示：枝条捡拾器属弹齿滚筒式结构，ΔABC在转动过程中形状是固定不变的，弹齿在围绕O点转动的过程中，同时受到滑道的束缚，产生摆动效果，并不断地变换空间姿态，完成捡拾过程的一系列动作。了解其基本结构及工作原理[4-14]，建立数学模型如下：

以O点为中心，建立坐标系，中心轴以ω的角速度顺时针匀速转动。设A点坐标为(x1,y1)，∠EOA=α，OA=r，α=ωt，t为时间(s)，则有

x1=rcosα

(1)

y1=rsinα

(2)

设弹齿AC与水平坐标轴夹角为β，弹齿长度AC=L2，C点坐标为(x2,y2)，则

x2=x1+L2cosβ

(3)

y2=y1+L2sinβ

(4)

设B点坐标为(x3,y3)，曲柄长度为L1，BC=L3,则

L12=(x3-x1)2+(y3-y1)2

(5)

L32=(x3-x2)2+(y3-y2)2

(6)

设弹齿与曲柄的夹角为θ，∠CAB=θ，根据余弦定理得

L32=L12+L22-2L1L2cosθ

(7)

由式(5)、式(6)得

x12-x22+2x3(x2-x1)+y12-y22+
2y3(y2-y1)=L12-L32

(8)

将式(7)代入式(8)，可得

x12-x22+2x3(x2-x1)+y12-y22+
2y3(y2-y1)=2L1L1cosθ-L22

(9)

式(9)、式(5)组成关于B点坐标(x3,y3)的二次二元方程式，假设方程式为

Py32+Qy3+R=0

(10)

(11)

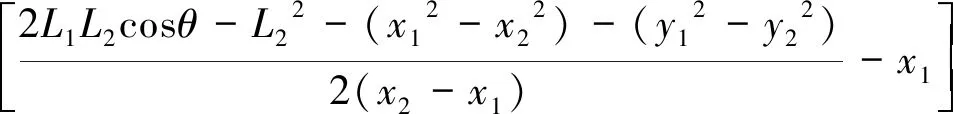
(12)

(13)

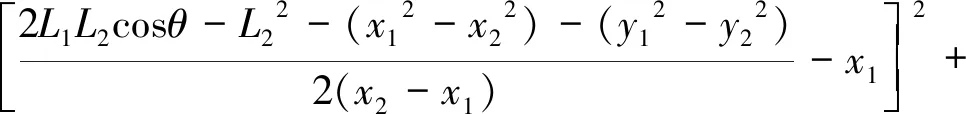
(14)

将式(12)～式(14)代入式(11)中，即可得两个y3值。将y3值代入式(9)，即可解得x3值，即

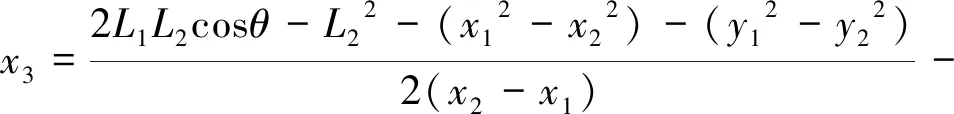
(15)

建立弹齿滚筒式捡拾器数学模型，由式(11)～式(14)可以看出：涉及的变量参数有L1、L2、L3、α、β、θ、r、ω和t等，A点坐标(x1,y1)与C点坐标(x2,y2)均可以由上述变量参数求得，因此B点坐标值(x3,y3)也能由上述变量参数求得。B点坐标是由上述变量参数决定的变化坐标点，B点坐标的变量精度是由旋转角度α的变化精度决定的，即为滑道任意点坐标值，将坐标点进行拟合，即为滑道函数曲线。

2 枝条捡拾动作多段分析

为了满足捡拾器“捡拾”地表上枝条的动作要求，将弹齿旋转1周视为1个周期，并对旋转十字架的旋转角度α进行分段设计。按照弹齿顺时针旋转方向，以x轴为起始点(见图1)，依次分为：①弹齿与枝条分离阶段，旋转角α1=∠EOD；②弹齿放齿划地聚拢枝条阶段，旋转角α2=∠DOH；③捡拾枝条阶段，α3=∠HOF；抬升回拢枝条阶段，α4=∠FOG；④向后推送枝条阶段，α5=∠GOE。

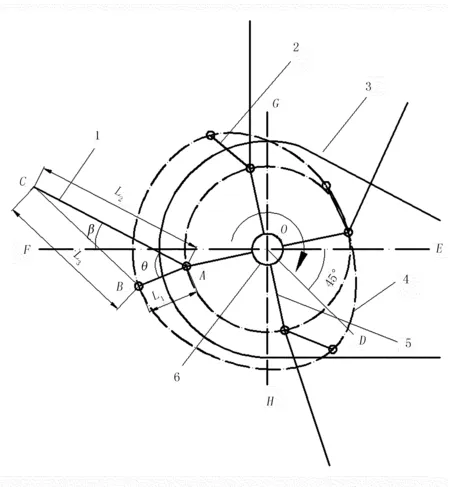
1.弹齿 2.曲柄 3.护板 4.滑道 5.旋转十字架 6.旋转中心轴图1 枝条捡拾器结构示意图Fig.1 Diagram of structure for pick up mechanical

(a) 弹齿与枝条分离阶段

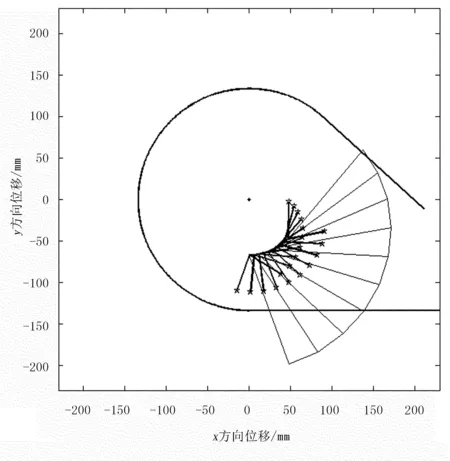
(b) 弹齿放齿划地聚拢枝条阶段

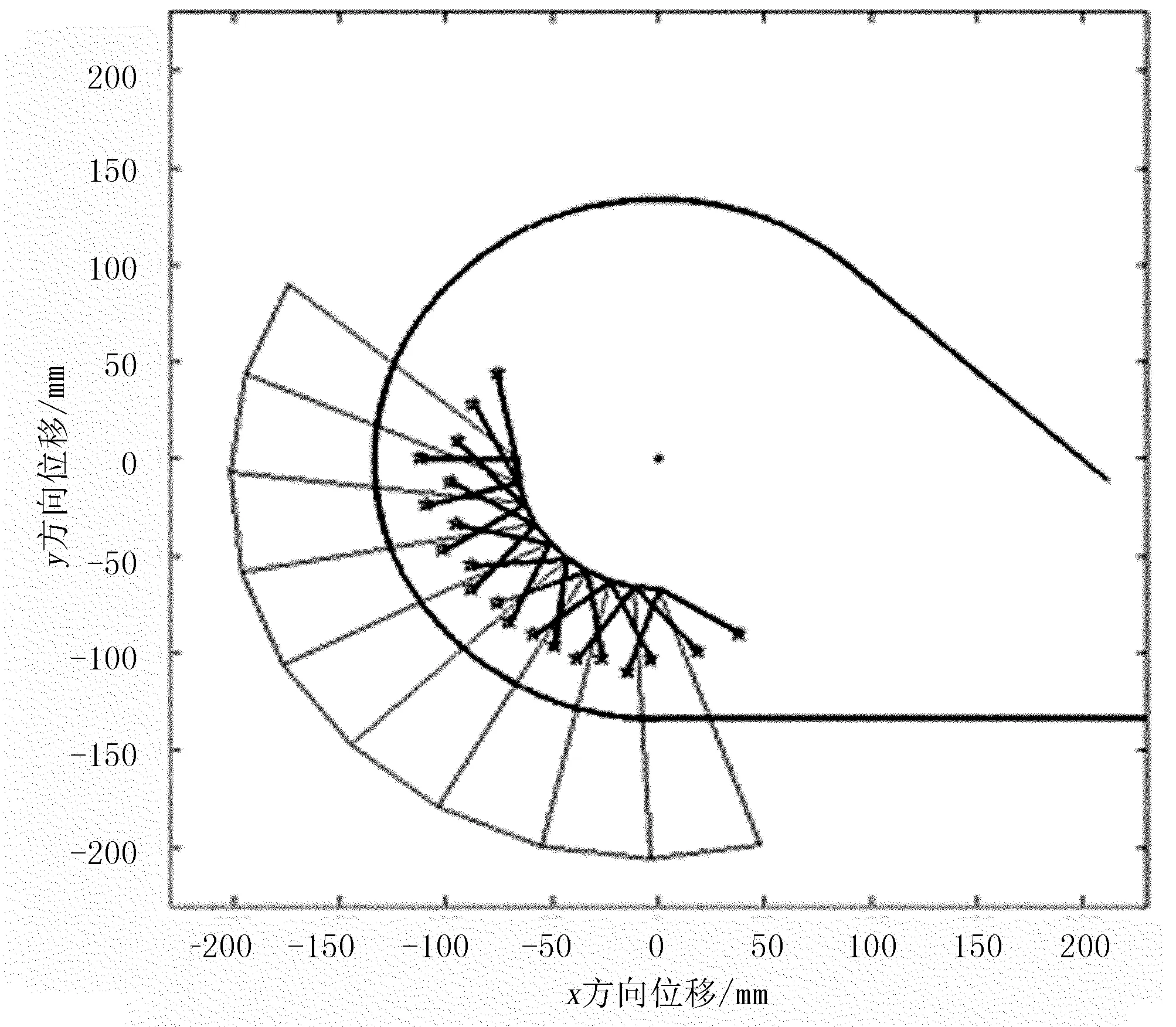
(c) 捡拾枝条阶段

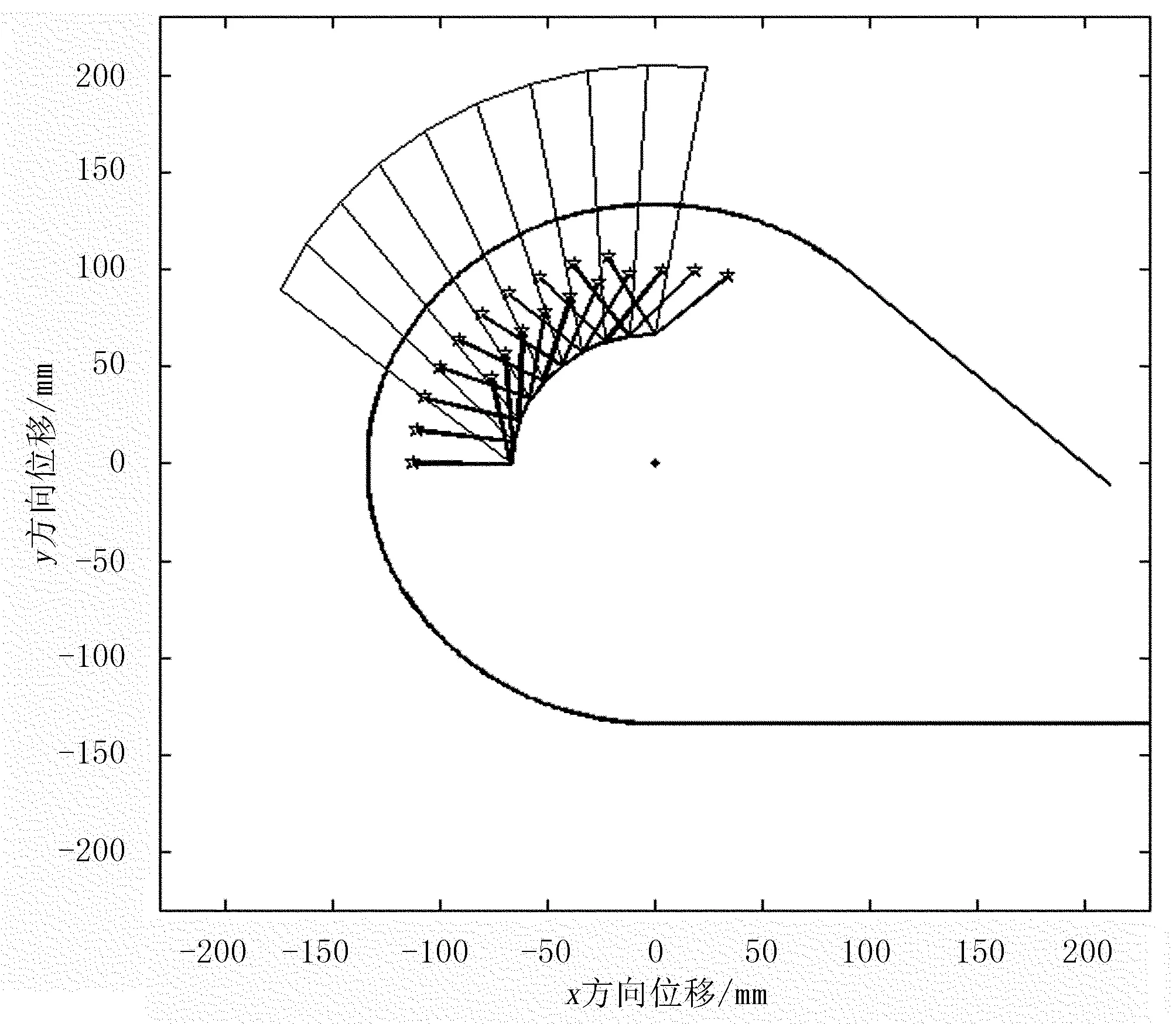
(d) 抬升回拢枝条阶段

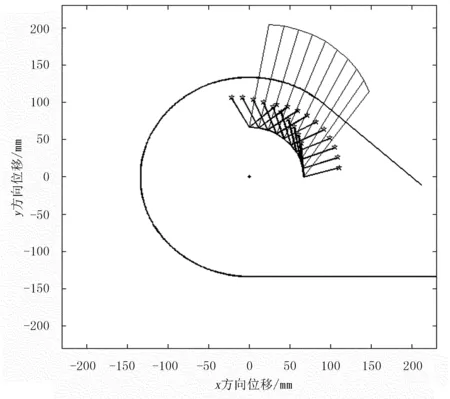
(e) 向后推送枝条阶段图2 弹齿转动各阶段运动轨迹Fig. 2 Spring-finger subsection running state

3 人机交互软件仿真与检验

弹齿尖端运动轨迹、弹齿空间运动姿态和滑道曲线运动轨迹与枝条捡拾效果密切相关。本文提出一种基于计算机人机对话的方法[16]检验并优化弹齿滚筒式枝条捡拾器的主要参数。通过虚拟仿真运动轨迹，优化并检验是否能够满足捡拾枝条并向后输送的动作要求[17-18]。

3.1 软件界面与功能介绍

人机交互软件是通过计算机编程，提取机构中的主要参数实行变量控制，充分发挥人的判断、经验等优势，结合计算机的强大计算能力，实现机械机构的虚拟仿真，并对主要参数进行检验和优化的方法。

软件界面的右侧上方是输入参数进行优化变量的区域，下方是输出图形和数据进行分析、判断的控制区域，软件界面的左侧是图形显示区域。软件中输入参数包括弹齿滚筒式捡拾器的变量参数L1、L2、α、β、θ、r、ω、t。其中，α、β分别可以根据捡拾枝条分解的动作要求对其进行分段设置，编制的程序最多可以分解成5段，分段时需要保证α、β周期循环且具有连续性。输出参数包括弹齿尖端运动轨迹、弹齿空间运动姿态、曲柄空间运动姿态、滑道曲线运行轨迹，软件左侧的图形显示窗口可以虚拟仿真捡拾动作，并采集所需要的具体数据。

如图3所示：软件程序编制了弹齿滚筒式枝条捡拾器运行1周，可以最多分解成5段的功能，也可以分解成更少的动作，但要保证α、β数值连续，不能产生脱离实际的跳跃值。

3.2 检验

由图4所示的弹齿运行轨迹可以看出：曲柄端点任意1个A点，都对应2个B点，即存在2个属于滑道曲线的函数值，这是因为ΔABC满足约束条件存在两种情况，分别是以AC为轴，镜像两侧存在两个滑道约束位置，也正符合上述数学模型中存在两个解的情况。

4 数据采集与后处理

弹齿滚筒式捡拾器虚拟仿真精度取决于数据节点的数量，同样的区间获取的数据节点数量越多，精度越高。如图5(a)所示，最初仿真得到的滑道数据是曲线2上的数据圆点，运用插值法对圆点进行函数运算，然后对这些数据点进行曲线拟合并进行平滑处理[20]，得到曲线2的函数曲线，即滑道曲线函数，如图6所示。

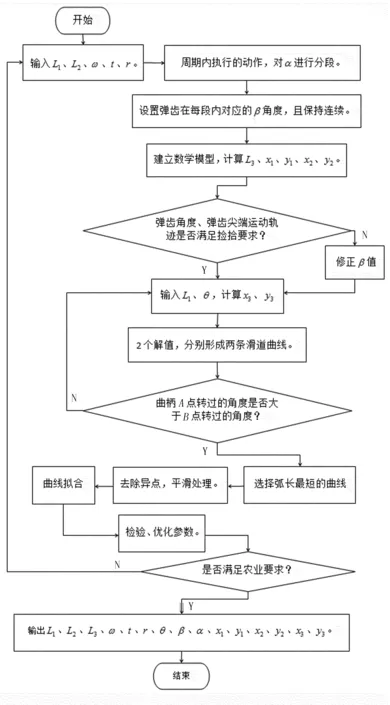
图3 软件流程图Fig.3 Flow diagram of software design

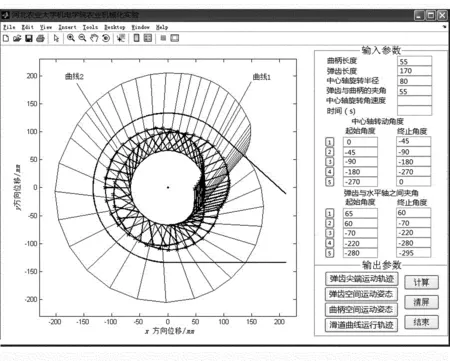
图4 曲柄运行轨迹与呈现状态Fig. 4 Result of optimization

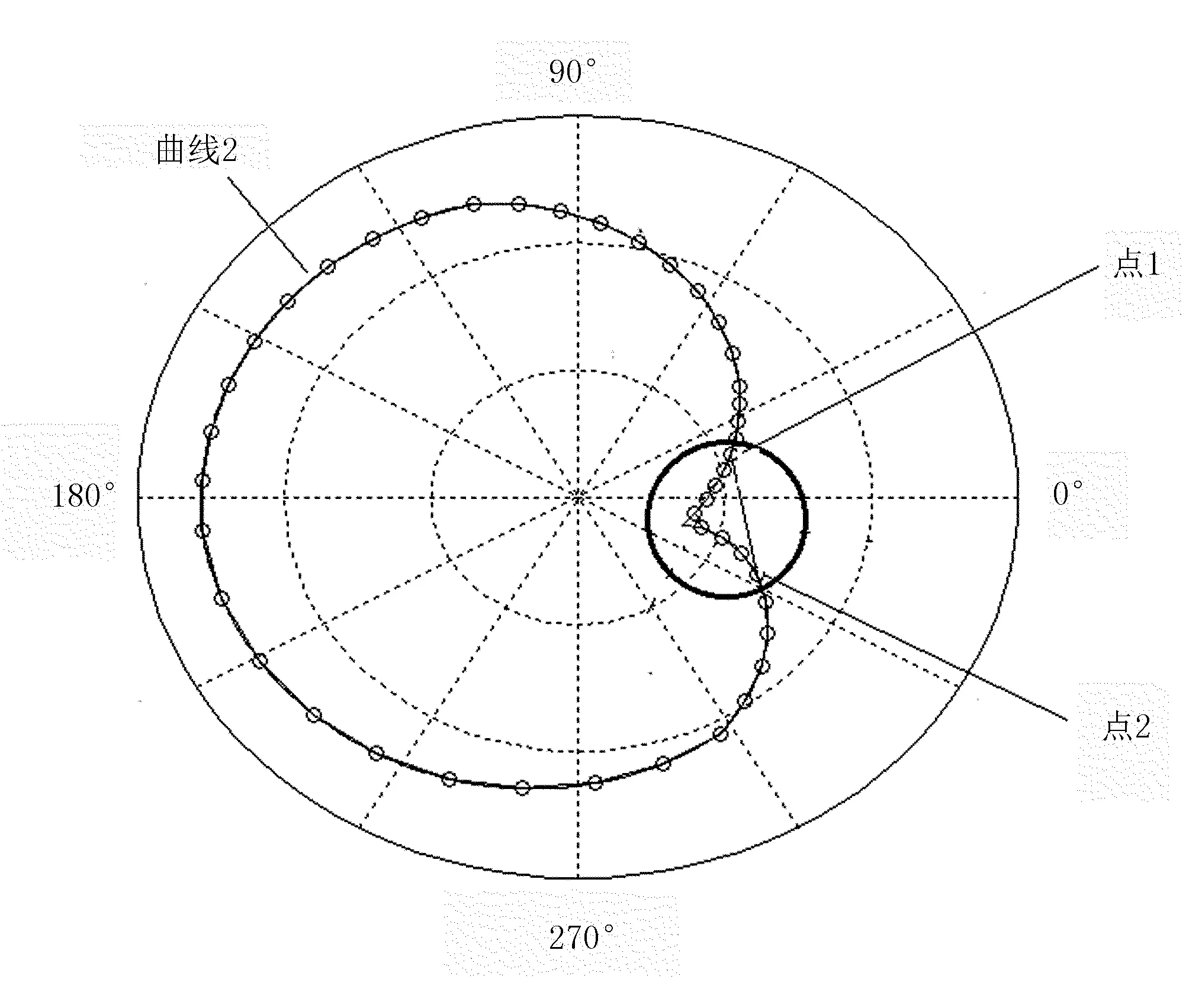
(a) 处理前

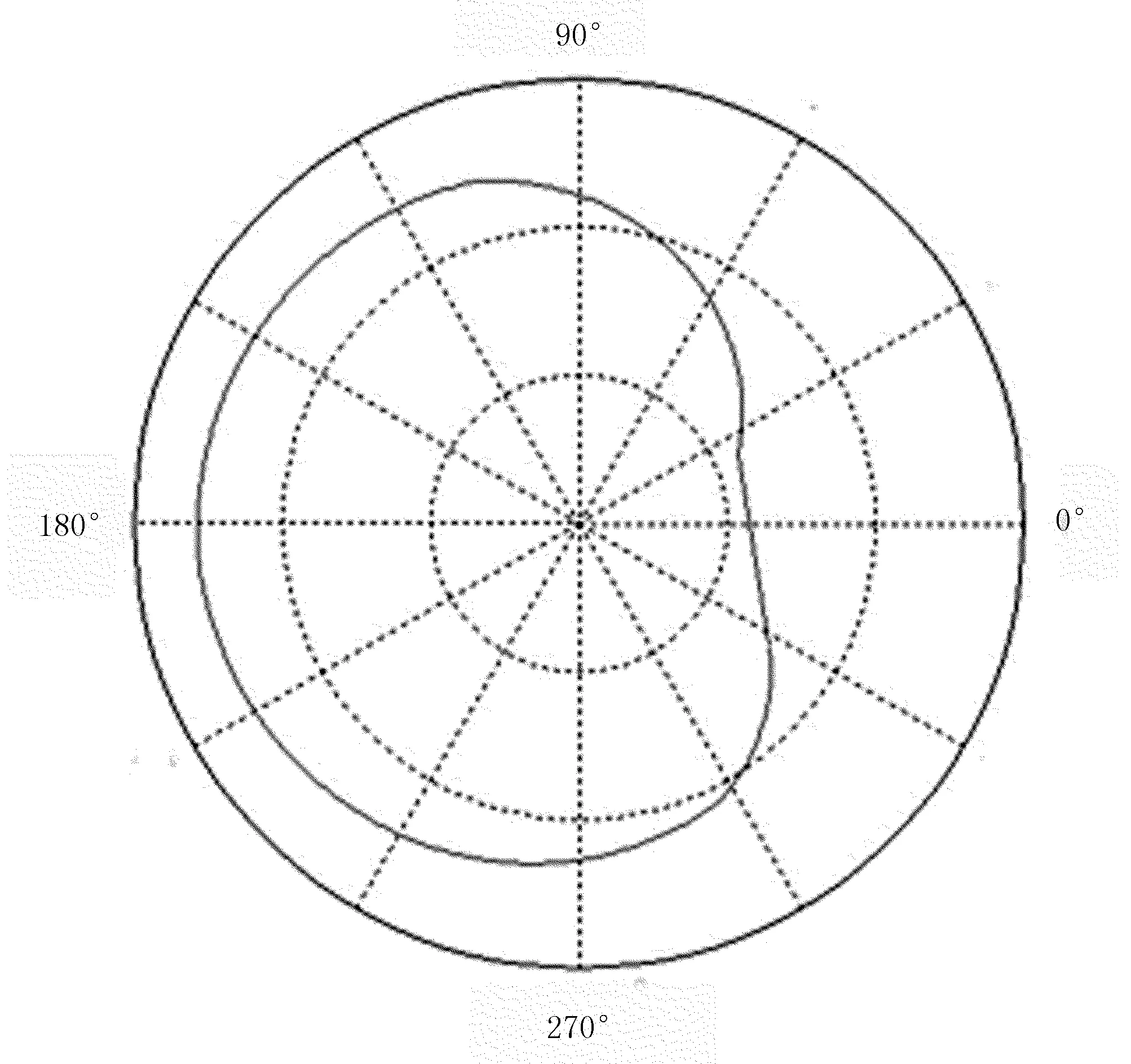
(b) 处理后图5 数据处理Fig.5 Date post-processing

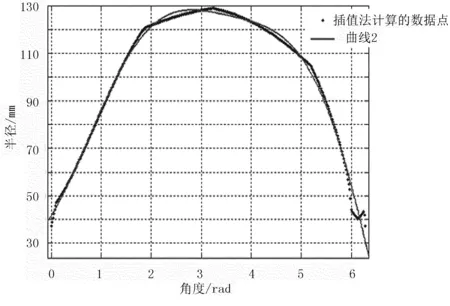
图6 多段曲线拟合Fig.6 Subsection curve fitting

曲线2的Fourier函数表达式为

f(x)=a0+a1cos(x·w)+b1sin(x·w)+a2cos(2x·w)+b2sin(2x·w)+a3cos(3x·w)+b3sin(3x·w)

其中，a0=38.69，a1=46.5，b1=76.06，a2=-33.46，b2=-33.33，a3=-10.13，b3=22.04，w=0.453。

当捡拾器正常运行时，曲柄轴承在滑道内快速滑动。当运行到图5(a)中圆圈内的突出点时，不能平滑地过渡，同时产生很大的冲击，影响滑道和曲柄的使用寿命。因此，需要对圆圈内突出的部分进行平滑处理。结合图3可以看到：当曲柄轴承运行到滑道的突出部分时，弹齿都处在护板以内的位置；当弹齿全部在护板内时，不会影响捡拾效果，只需要将尖突部分删掉。根据显示窗口中弹齿与护板的相对位置，可以判断出点1和点2的具体位置，然后由直线连接两点。如图5(b)所示：滑道曲线是由一段曲线和一条线段组成的，曲线与线段连接处平滑过渡，即满足捡拾动作要求，又缩短了滑道的孤长，增加了零件使用寿命。

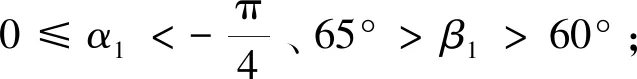
5 结论

1)通过分析弹齿滚筒式捡拾器结构，建立了数学模型。经过分段设置弹齿空间运行姿态来满足捡拾动作的要求，利用反求法对滑道中心函数曲线进行求解，再经过数据的后处理，满足了枝条捡拾器设计目标的要求。

2)使用人机交互软件的方式，对弹齿滚筒式枝条捡拾器进行模拟，优化相关参数，人与计算机互相配合，能够实现基于类比设计方法的弹齿滚筒式捡拾器参数求解、动态仿真、数据采集与后处理的数字化设计过程。