聚变激光等离子体相互作用中受激拉曼散射动理学数值模拟研究进展

刘明明，李 棚，邹长林

(1.六安职业技术学院 信息与电子工程学院，安徽 六安 237158；2.安徽理工大学 电气与信息工程学院，安徽 淮南 232001)

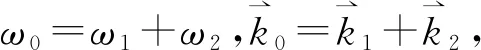
在激光与等离子体相互作用中，粒子和场的集体相互作用是一个强而复杂的非线性问题。传统上，研究该系统主要是通过理论和实验工作，发展分析模型来确定目标系统的行为，然后再通过复杂的实验来观察其随时间的演化。但激光等离子体的瞬时相互作用和极其复杂的多自由度使得解析解变得不实际。而在实验上观察激光等离子体相互作用的许多重要细节也是极其困难的。因此，需要其他的手段来进一步加深对这个领域的理解。

基于高性能计算机技术的发展，数值模拟如今已得到空前发展，以致它已成为独步理论和实验之外的单支学科，逐渐展示着其在理论模型建立和实验结果理解上的价值。当前清晰且详细地理解激光等离子体相互作用的物理机制只有借助于理论，实验和数值模拟三者的结合[2]。数值实验可以提供我们想要的各种系统演化的信息。研究者可以使用每次模拟的结果来检测基于简单分析模型给出的预期值，或者将其与实验结果进行比较，来推测实验上难以获得的细节。最终，在建立适当的基准之后，这个工具就可以被用于预测未来实验的结果，并有助于指导这个领域内实验的可努力方向。

1 动理学数值模拟研究的方法

通常，等离子体中的粒子都不是碰撞平衡(如麦克斯韦分布)。这种平衡性导致的差别使得等离子体有别于流体或固体力学，并引发出一些最重要的等离子体行为。我们对于遵循等离子体在相空间(坐标和动量)中演化的动理学模型十分感兴趣。在概念和计算上动理方程数值求解相比于流体方程更能满足要求。目前有两种方法被用于模拟动理方程：欧拉(也称为Vlasov)方法和Particle-In-Cell(PIC)或拉格朗日方法。Vlasov方法中视等离子体为“相空间中流体”，而不是离散型宏粒子的集合。在相空间中的固定网格上通过求解动理学方程以获得分布函数f(x,p)。换句话说，PIC方法用一个离散有限大小粒子集合(宏粒子)来替代f(x,p)，它们可以在相空间中自由移动。

两种方法都有其优点和缺点。PIC方法的优点是所需宏粒子的数目随着计算维数的增加而并不快速的相应增加。这使得PIC代码得到空前的发展，并实现了商业化。但是PIC方法存在产生于单粒子的高噪声问题。它等同于实际等离子体中的物理涨落(这种涨落振幅是很小的，因为在物理德拜球中的粒子数目远大于PIC模拟中的数目)。高噪声水平使得PIC方法很难用于研究线性和弱非线性。在连续性方法中，我们视分布函数f为一相空间流体，它没有产生于PIC方法中单粒子运动时的涨落或噪声。我们要付出的代价是更多的相空间网格和计算机内存，运行时间，尤其是在高维的情况中。但随着超级计算机的计算能力的指数级增长，使得Vlasov代码正变得越来越流行。

1.1 Particle-In-Cell方法

描述无碰撞等离子体的相对论运动方程[7]

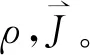
随后在网格上求解。这里ε0,μ0是真空中的介电系数和导磁率。重复迭代方程组(1)和(2)，我们就得到了等离子体和场在时空中的自洽演化。

(3)

PIC方法包含两个部分，粒子推动和场的求解。如图1所示，粒子推动部分使用离散在网格上的电场，通过洛仑兹力，计算粒子的加速；并且根据新的速度将粒子推动到新的位置。之后，粒子的电荷和电流将沉积到网格上。在场的求解部分根据麦克斯韦方程来推进电场和磁场。

图1 PIC方法的计算流程图(虚线框部分考虑的是蒙特卡洛碰撞)

1.2 Vlasov方法

我们考虑等离子体仅是在x轴(纵向)上变化(∂/∂y=∂/∂z=0)。等离子体会与纵向静电场Ex和横向电磁场Ey,Bz(y方向(横向)上线性极化)。在y方向上，我们视等离子体为冷流体，都具有同样的横向速度vy(x,t)。这个横向流会将纵向(x)和横向(y)动力学耦合在一起。动理学方程为[8](P27-35)

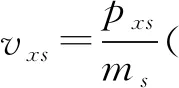
一维无碰撞(νCs=0)Vlasov代码基本算法主要是基于三次样条插值[8]，利用分步法将fs由t时刻推动到t+dt时刻。将时间步分为在x空间中是自由流运动，在px空间中由电磁力推动粒子加速。首先利用自由流Vlasov方程

(5)

将fs由t推动到t+dt-。利用Poisson方程(4b)由新时刻的密度ρ(t+dt)计算出Ex(t+dt).然后利用Jy(t+dt/2)计算出方程(4c)中的E±，我们现在可得到Ey(t+dt)，并利用它将vy由t+dt/2推进到t+3dt/2时刻。最后，在动量空间中利用方程

(6)

计算出t+dt时刻的fs。

2 受激拉曼散射模拟研究进展

以聚变中激光与等离子体相互作用中SRS为研究对象，国内外的学者做大量工作。以三波耦合模理论分析为基础，北京应用物理与计算数学研究所曹莉华研究员课题组研究了小带宽频率啁啾对SRS的影响，得出频率啁啾对后向SRS有抑制作用，且后向散射不依赖于啁啾符号[9]；正(负)啁啾对前向SRS有微弱的增强(减弱)的作用。粒子模拟(PIC)和理论分析结果一致。中国科学技术大学郑坚教授课题组对耦合模方程组做数值计算研究了稳态近似条件下噪声源对后向SRS反射率的影响[10]。Benisti等利用耦合模理论推导了SRS阈值强度并与Vlasov代码比较分析了SRS不稳定中朗道阻尼率的非线性降低以及等离子体波的非线性波数和频率移动[11-12]。这些耦合模稳态近似分析中忽略了不稳定性系统的时间演化特性，同时流体三波耦合模型并没有体现最具决定性意义的等离子体动理学特性。

以PIC模拟为研究手段，Vu首先提出被捕获粒子可以导致等离子体波的频率和阻尼率出现非线性降低[13]，前者将导致等离子体波与入射波和散射光波之间的三波共振失谐，于是SRS达到饱和。Yin等利用三维VPIC程序得出高维情况下动理非线性频移效应[14-15]。在中心处大振幅的有限宽度等离子体波(相对于边缘)具有较大的频移。随着相移累积，波前将变得“弯曲”。最终被捕获粒子的调制不稳定性导致波开始“自聚焦”[16]，如图1所示。该过程使得等离子体波越来越窄，进而SRS过程开始熄灭并达到饱和。Fahlen等利用三维静电BEPS程序研究指出[17-18]，在kλD≥0.2时，中心轴附近的横向上出现大振幅波，波中心近似为平面波，振幅近似为常量，也即被捕获粒子处于准稳态并在较长时间内得到维持，同时横向边缘受到阻尼。由于依赖波振幅的负频移效应，有限宽度波的中心相对于其边缘累积了一定的相移，于是波的横向边界逐渐向中心轴收敛。在耦合模方程中引入Morales-O’Neil非线性频移的理论表达式[19]，Chapman等研究的非均匀等离子体中SRS自共振现象[20]，其中空间非均匀性导致正频移与被捕获粒子导致的负频移相互抵消，也即SRS三波不稳定性维持共振增长。

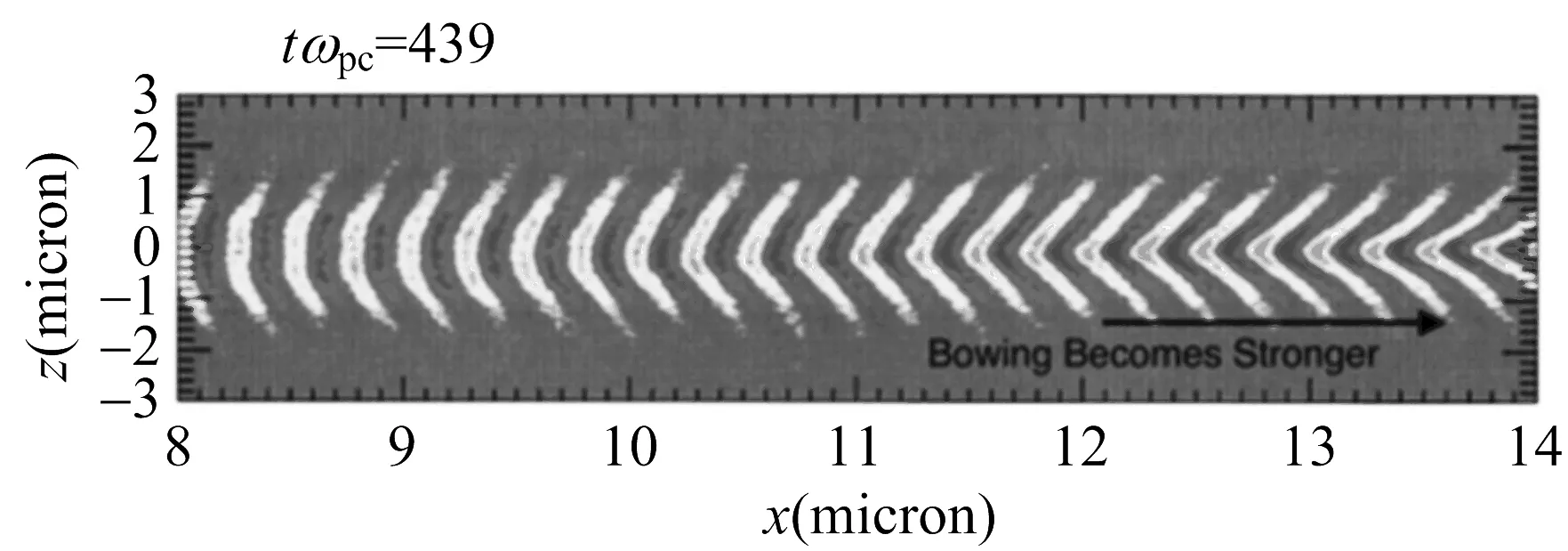
图2 非线性频移导致的波前弯曲[16]

利用RPIC程序，Vu等[13]得到的反射率要远大于强阻尼极限下对流增益理论计算值。他们认为被捕获粒子导致朗道阻尼率非线性降低，于是在阈值强度处反射率快速增大，也即“动理增强”，如图2所示。反射率的突然增大是因为不稳定性由强阻尼转换到弱阻尼。Vu等随后又建立了“动理增强”效应的理论模型[22]，进一步指出该效应是速度扩散和捕获竞争的结果。以三波耦合理论分析为基础，我们利用PIC代码模拟研究了后向SRS不稳定性的跃变属性参数范围及其对平均反射率的定量影响[7]。

图3 SRS平均反射率在阈值强度处跃升，在更高强度处达到饱和[21]

图4 不同强度两个散斑激光入射到等离子体中，Ex(ωpet=3417)表明两个散斑中都建立了SRS的子波-电子等离子体波[24]

多散斑激光入射均匀和非均匀等离子体中时，SRS饱和及热电子输运的影响也得到充分研究[23-24]。如图3所示，研究表明当SRS中电子等离子体波出现波前弯曲并成丝时，强度高的散斑中以及前向和侧向散射中产生的热电子都会通过降低的朗道阻尼使得强度弱的散斑中SRS增长率增强，也就是说散斑中电子捕获增强的三波相互作用通过电子输运、后向散射和侧向散射使得强弱两个散斑出现自组织并展现相干性。这时SRS的饱和水平取决于kλD，反射率正比于(kλD)-4，当kλD和朗道阻尼增大，散斑间的相互作用减弱，相应SRS时间平均反射率也降低。

国防科技大学卓红斌教授和上海交通大学盛政明教授课题组利用一维粒子模拟代码验证了当激光带宽远大于线性增长率时，带宽对SRS的线性增长阶段具有明显的抑制作用[25-27]。

Vlasov数值模拟方法是在相空间中固定的欧拉网格上通过求解动理方程以获得分布函数f(x,p)的演化，因此没有PIC方法中单粒子运动时的涨落或噪声。由于复杂的数值方法和大量计算资源的占用，致使利用Vlasov方法模拟研究SRS不稳定性物理的学者还较少，研究的内容主要侧重不稳定性中等离子体波物理属性及其对SRS的影响，且这些代码都是一维的。Brunner等利用开发的SAPRISTI代码主要是研究电子等离子体波和离子等离子体波(受激布里渊散射(SBS)中的次级子波)的非线性频移和边频不稳定性效应[28]。Strozzi等利用开发的ELVIS代码研究了Single-Hot-Spot和NIF两种参数下后向SRS中静电波非线性频移效应和电子声汤姆孙散射。北京应用物理与计算数学研究所的刘占军等利用开发的代码研究了SRS激发的太赫兹辐射、电子-离子碰撞效应对后向SRS反射率的影响和SBS效应[29]。随着计算机性能的飞速提升，Vlasov方法因其无数值噪声特性将受到越发广泛的关注，特别是在线性和弱非线性激光-等离子体相互作用问题中的应用[30]。

3 结语

SRS是激光聚变中的关键物理问题之一，对于聚变工程来说，人们追求的是建立高科学置信度的激光聚变全过程数值模拟分析[31]。目前虽然在各个方向上取得了一系列进展，但是有待解决的问题依然很多，包括物理建模、数值计算方法及相关程序研制等。例如在建模过程中要充分考虑波-波、波-粒子相互作用的SRS、SBS以及自聚焦等耦合效应。由于等离子体密度密切影响激光等离子体相互作用，通常简单扣除受激散射激光能量的处理方式，难以反映其对辐射驱动对称性的影响。随着高性能计算机技术的高速发展，计算机结构和并行程序结构都变得异常复杂，这给激光聚变应用程序的发展带来巨大挑战。高效应用好计算机数值模拟分析，以进一步推动聚变工程的研究进展，人们还需要面对高性能模拟应用程序研制周期和运行效率问题。尽管如此，这依然是一个有着巨大潜力的朝阳领域，相信未来令人瞩目的成果会不断出现。