二维磁流变包层声学超材料∗
2019-05-22许振龙吴福根
许振龙 吴福根
(1 广东科学技术职业学院机械与电子工程学院 珠海 519090)
(2 广东工业大学材料与能源学院 广州 510006)
0 引言
声子晶体和声学超材料具有声波或弹性波禁带,声波或弹性波在禁带中无法传播[1−3]。声子晶体产生禁带的机理是布拉格散射,要求晶格尺寸与声波波长在同一数量级。声学超材料是亚波长尺寸的人工微结构,可以调控和操纵波长高于晶格尺寸两个数量级的声波的传播。通过对声学超材料微结构单元加工和设计,可以实现许多具有应用前景的特殊性能,如负折射与超透镜[4]、双负折射与反向多普勒效应[5]、零折射率与全反射[6]、亚波长检测[7]、全方位声学斗篷[8]等。
Liu 等[9]构建出局域共振型的声学超材料,局域共振型声学超材料禁带对应的波长远远大于晶格的尺寸,单元尺寸可以很小,使得低频噪声和振动控制的元件化成为可能。研究人员在局域共振型超材料方向做了许多努力。Larabi 等[10]设计了多层交替排列的同轴圆柱形局域共振型超材料。Bonnet等[11]设计了硬核和包层组成的圆柱形和球形复合超材料结构,结果表明在理想模型下,通过组分和形状的优化可以得到最低的共振频率。Wang等[12]设计了金属核芯通过弹性梁连接到弹性体基体的局域共振型超材料,在宽频率范围内实现带隙的可调谐,还利用变形来打开或关闭带隙。Yang 等[13]使用有效质量密度的拓扑优化方法来最大化局域共振型超材料的第一个带隙。Chen 等[14]提出了一种由多层黏弹性连续介质组成的耗散局域共振型超材料,可以有效衰减瞬态冲击波。Krushynska等[15]设计了二维和三维双局域超材料结构。
含磁性材料的超材料研究正逐渐展开[16]。磁流变弹性体是由磁性颗粒分散在天然橡胶或硅橡胶基体材料中组成。外加磁场条件下,弹性体中磁性颗粒会形成链状聚集结构[17−19]。磁流变弹性体克服了磁流变液易沉降、稳定性差的缺点,具备响应快、可逆性好等优点。Xu 等[20]设计了一维二组分和三组分的声子晶体磁流变隔振支座,结果表明其存在着完全声波带隙,并且可以通过外磁场调节其带隙宽度和位置。Alireza 等[21]设计了多孔磁流变弹性体局域共振型超材料,研究了不同变形、不同外磁场作用下的能带结构,证明大变形和外磁场可以改变带隙的位置和宽度。
根据研究现状,设想以磁流变弹性体作为超材料局域共振单元硬核的包层,实现弹性系数的可调。文中计算采用有限元方法,研究结果表明:通过外磁场控制磁流变弹性体包层,或者调整磁流变弹性体包层的厚度,都可以调节局域共振型超材料声波禁带的宽度和位置,这些将为声学超材料设计提供新的思路。
1 模型和方法
图1(a)为磁流变弹性体包层局域共振型声学超材料示意图,各个共振单元如图周期排列,磁流变弹性体包层可以通过外磁场调节控制其弹性模量。图1(b)为圆形内核声学超材料结构单元,周期晶格常数a= 0.025 m,钨圆形内核半径为r1,包裹磁流变弹性体后半径为r2。
对于二维弹性各向同性介质,波动方程表示为

图1 磁流变弹性体包层局域共振型声学超材料和圆形内核声学超材料结构单元Fig.1 Local resonance acoustic metamaterial with magnetorheological elastomer cladding and acoustic metamaterial unit with circular core
本文计算采用有限元方法,方法已广泛应用于声子晶体能带结构计算,用于处理复杂材料结构时有明显优势。文中采用钨的密度ρt=19.3×103kg/m3,其纵波波速为Ctl= 5.09×103m/s,横波波速为Ctt= 2.80×103m/s。环氧树脂密度ρe= 1.2×103kg/m3,其纵波波速为Cel=2.83×103m/s,横波波速为Cet=1.16×103m/s。
磁流变弹性体计算采用磁偶极子模型,Fe颗粒密度ρFe= 7.89×103kg/m3,橡胶密度ρr= 1.2×103kg/m3。采用磁流变弹性体的拉伸性能与剪切性能近似,其泊松比取0.47[22]。剪切模量的改变量与外磁场关系为[23−24]
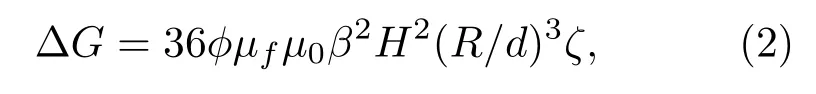
式(2)中,ϕ是基体中的Fe 颗粒的体积比,R是Fe颗粒半径,d是聚集状态链中的两个颗粒之间的距离,µ0是真空磁导率,H为外部磁场磁场强度,ζ ≈1.202,β ≈1,µf= 1 是相对磁导率。假设d/R= 2.5,ϕ= 27%,并采用典型的弹性参数G0=0.4 MPa。
2 计算结果和讨论
如图1(b)圆形内核局域共振型超材料单元,设计的圆形钨内核半径r1= 0.01 m,包裹磁流变弹性体后半径r2= 0.0105 m,即磁流变弹性体厚度为d= 0.0005 m。图2是圆形内核超材料系统声波能带结构图及对应ΓX方向的透射系数图。超材料单元中密度大的钨块充当质量块,密度小的环氧树脂作为基体,磁流变弹性包层起到弹簧的作用。系统中钨质量块和环氧树脂基体的密度相差较大,声波传播时会产生运动失谐,在低频处呈现负等效质量密度。由于钨块的质量较大,在特定频率处,几乎集中了声波传递的全部能量,所以在1407 Hz 和11600 Hz 附近,可以看到一些平直的能带。平直的能带对应的模态的波速度为零,此时结构中无频散。平直能带频率对应于局域模态,如果特定频率声波入射到超材料系统中,和局域模态发生作用,会出现局域现象。声波无法用其他非局域态方式通过周期结构,因此能带被分裂,从而产生局域带隙。可以看到在1407∼5799 Hz 之间出现一个较大的完全带隙,图右侧是对应ΓX 方向的透射图,在带隙范围内出现较大的衰减,在局域频率处衰减最强,出现不对称的透射尖峰,这是局域共振Fano 现象的典型特点。这些结果表明:采用磁流变弹性体为包层的二维圆形内核超材料单元,在低频处存在声波局域共振完全禁带。
图3(a)是圆形内核声学超材料668 Hz 时Γ点的振动模态图,图3(b)是1407 Hz 时X点的振动模态图,可以看到圆形内核钨质量块内核呈自旋态或传播状态,超材料单元的振动集中在钨质量块上,包层和基体的振速/振幅几乎为0,所以带隙的下边沿的振动模式可以看作一个圆形内核质量块的振动,相邻晶格之间的振动相位的周期性保持了整个系统的动态平衡,系统进入禁带状态。此时系统可以简化为质量弹簧系统如图3(c)所示,其中模块M表示钨内核等效质量块,弹簧k表示包层的等效刚度。带隙的下边缘的频率可以估测为
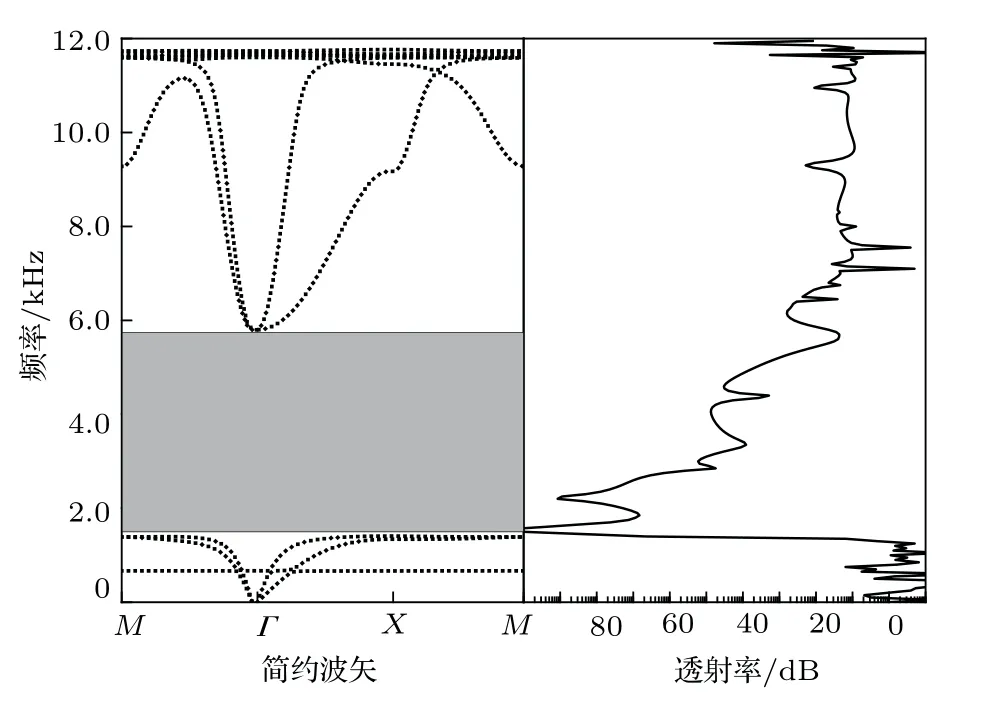
图2 圆形内核声学超材料声波能带结构及ΓX 方向透射系数Fig.2 Acoustic wave band structures and corresponding ΓX-direction transmission curve of acoustic metamaterial with circular core
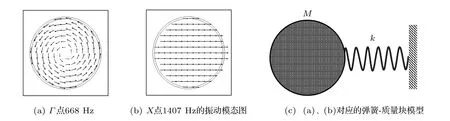
图3 声学超材料带隙下边沿的振动模态图及对应的弹簧-质量块模型Fig.3 Acoustic metamaterial vibration mode of the lower edge of the band gap and the corresponding spring-mass model
图4(a)是圆形内核声学超材料禁带上边沿5799 Hz时Γ点的振动1模态图, 图4(b)是5799 Hz时Γ点的振动2 模态图,可以看到圆形内核钨质量块与包层、基体介质的一起振动,系统从此进入允许弹性波传播的导带状态。此时系统可以简化质量弹簧系统如图4(c)所示,其中模块M表示钨质量块,m表示基体的质量,弹簧k表示包层的等效刚度。带隙的上边沿的频率可以估测为

图4 声学超材料带隙上边沿振动模态图及对应的弹簧-质量块模型Fig.4 Acoustic metamaterial vibration mode of the upper edge of the band gap and the corresponding spring-mass model
图5为局域共振型声学超材料系统(r1=0.01 m,r2= 0.0105 m)声波带隙与外磁场强度的关系。施加一个从0 kOe到10 kOe平行于磁流变弹性体的磁场(图1(a))。当外磁场强度H= 0 kOe至H= 10 kOe,带隙频率范围从1407∼5799 Hz 变化为2210∼8980 Hz。可以看到,随着外加磁场增强,带隙逐渐增大,而且带隙的中心位置明显向上移动。分析其原因是外加磁场改变了磁流变弹性体弹性模量,弹性模量决定着包层的弹性系数,外加磁场越强,弹性系数k就越大。根据上下边沿频率的估测方法,带隙上下边沿的频率随着弹性系数k增大,带隙中心位置上移,上移过程中带隙上边沿的频率增大得更快。随着磁场增强,带隙越来越大。可以总结出,局域共振型超材料的声波带隙受外磁场的影响,调节外部磁场强度可以调节带隙的中心位置和带隙宽度。

图5 声学超材料声波带隙与外磁场的关系Fig.5 External magnetic field as function of acoustic metamaterial acoustic bang gaps
图6为当外磁场强度H= 0 kOe,局域共振型声学超材料声波带隙与磁流变弹性体包层厚度的关系。保持晶格周期a=0.025 m和r1=0.01 m不变,调整磁流变弹性体包层厚度从d= 0.0002 m 到d= 0.002 m,带隙频率范围从2204∼9002 Hz 变化为712∼2360 Hz。可以看到,随着磁流变弹性体包层厚度的增加,其声波带隙中心位置下移,带隙宽度逐渐减小。分析其原因是磁流变弹性体包层厚度增加,包层的等效刚度降低,包层弹性系数k减小,带隙上边沿比下边沿减小得更快,导致系统带隙宽度减小,中心位置下移。结果表明,声波带隙对包层厚度是敏感的,通过调节包层厚度,可以调节带隙的中心位置和宽度。

图6 声学超材料声波带隙与磁流变弹性体包层厚度的关系(H =0 kOe)Fig.6 Magnetorheological elastomer cladding thickness as function of acoustic metamaterial acoustic bang gaps (H =0 kOe)
3 结论
本文用磁流变弹性体作为包层设计了二维局域共振型声学超材料。超材料周期单元中,圆形钨内核为质量块,环氧树脂为基体,磁流变弹性体相当于弹簧。用有限元方法进行计算,分析了系统能带结构、声波透射率、振动模态等,结果分析表明:外磁场可以调控磁流变弹性体包层的弹性系数k,调控带隙上下边沿的频率,从而调节带隙的中心位置和宽度;还可以调控磁流变弹性体包层的厚度来调节二维局域共振型超材料带隙的中心位置和宽度。这些方法对声学超材料的可调谐应用设计有一定的借鉴价值。
