陕北黄土区SRTMDEM精度对不同地形因子的响应

高志远, 谢元礼, 刘 状, 蒋广鑫

(1.西北大学, 西安 710127; 2.陕西省地表系统与环境承载力重点实验室, 西安 710127)

SRTM DEM(Shuttle Radar Topography Mission)是全球最常见的免费中分辨数字高程模型之一，在土壤侵蚀、水土流失、流域分析、地貌分析等地理学各个领域都有着十分广泛的应用。SRTM DEM的精度相较于另一种常见的中分辨率数字高程模型ASTER GDEM，不但在绝大部分区域内精度优于ASTER GDEM[1]，并且SRTM DEM在地形较为复杂的地区其误差与地形具有较强的相关性[2]，即其误差随地形变化的敏感性较ASTER GDEM更强，因此利用SRTM DEM作为数据源进行精度与地形因子研究较为合适。

现阶段，SRTM DEM精度评价研究已取得了不少进展，Rodriguez等[3]利用USGS发布的NED(National Elevation Dataset)数据集作为高程标准数据，对全美SRTM DEM进行了精度评价。Manas等[4]利用动态全球定位系统，对全球6个大陆的SRTM DEM产品的绝对高程误差和相对高程误差进行了评估。而后Mukul等[5]又提出利用全球定位系统网络IGS(International Global Navigation Satellite System Service Network)分别对X波段和C波段的SRTM DEM数据进行了全球性的精度比较和评估。Zhao等[6]人利用ICESat/GLAS数据对中国中部地区的ASTER GDEM与SRTM DEM数据进行精度比较分析。詹蕾等[7]以我国1∶5万比例尺DEM数据作为参考数据，利用空间插值的方法对全陕西省的SRTM DEM数据进行了精度评价。在地形因子的研究中，张泉等[8]提出SRTM DEM误差与不同地形和地表覆盖密切相关，坡度增大，误差由正变负，误差绝对值增大。张朝忙等[9]在研究中国地区SRTM DEM精度时提出DEM数据高程精度受地形影响并存在一定的空间分布性。杜小平等[10]提出DEM的高程误差随地形起伏增加而增加。南希等[11]提出DEM数据垂直精度对坡度有较大的依赖性，且中误差随坡度有近似指数的曲线的增长趋势。可以说不管是全球大尺度还是地区小尺度，SRTM DEM的研究工作已有不小进展，但针对影响SRTM DEM精度的地形因子的研究工作却比较少，在以往的研究工作中，研究者也倾向于将研究精力投入在DEM精度的评估工作，而涉及到地形因子的影响性时也偏向于做定性的试验性结论陈述，而未做详细的定量研究。本文利用ICESat/GLAS GLA14陆地测高数据作为高程标准数据，结合不同的地形因子综合分析，对1弧秒SRTM DEM精度随地形因子的变化进行定量化研究。

1 研究区概况和数据

1.1 研究区概况

研究区以陕北典型黄土沟壑地貌为主要研究地貌类型，其大致范围为东经108.7°—110.5°，北纬37.0°—38.1°。包括了陕西省延安市的子长县和安塞县的一部分，以及榆林市的子洲县、米脂县全境和横山县、靖边县、佳县与绥德县的部分地区，总面积约为20 000 km2。黄土沟壑地区沟壑纵横、地形破碎、地形起伏度较大，各种地形因子变化较为明显，因此把黄土沟壑地区作为DEM地形因子评价的试验样区是比较合适的。

1.2 研究数据及处理

本文中研究数据分为两种，一种是SRTM DEM数据，将其作为精度评估原始数据，具体为SRTM1 Arc-Second Global，其空间分辨率为30 m，下载自(https:∥earthexplorer.usgs.gov/)。第2种是GLA14测高数据，GLA14(Global Land Surface Altimetry Data)数据隶属于ICESat/GLAS数据集中的二级产品，由GLA 05和GLA 06数据再生产，其传感器每秒发射40次脉冲亮斑，星下光斑点的直径为70 m，沿卫星轨迹相邻两光斑间隔为170 m，GLA14水平精度为±20 cm，垂直精度为±18 cm[8-9]。综合比较两种数据可以看出，GLA 14数据较SRTM DEM数据具有较高的精度，其垂直精度和水平精度都达到了cm级，因此可以作为评测SRTM DEM精度的标准对比数据，GLA 14数据来源于美国国家冰雪数据中心，下载自(http:∥nsidc.org/)。

2 研究方法

2.1 精度评价指标

在本文研究中，引用4个指标量作为精度评价及地形因子分析的参考指标，分别为高程误差d、平均误差Mean、标准偏差SD和中误差RSME。高程误差d代表了每一个GLA14数据点与对应SRTM DEM栅格点的差值(HSRTM-HGLAH14)，平均误差Mean是高程误差的平均值，是数据集中误差的平均体现。标准偏差SD表示高程误差之间数据离散的程度。中误差RSME是指测量值与真值之间的离散程度，是对测量值精度最直接的评价。4种指标公式如式(1—4)[10-13]所示。

d=HSRTM-HGLA14

(1)

(2)

(3)

(4)

2.2 地形因子与地理探测器

本研究中，引入高程、坡度、坡向、总曲率、平面曲率以及剖面曲率6种地形因子对SRTM DEM精度进行相关性分析。除了常规的几种地形因子高程、坡度和坡向外，还涉及到了3种曲率因子，其中平面曲率反映了地形在等高线方向的变化率，表达了坡向的变化;剖面曲率是一种对地形在最大坡度方向上高程的变化的度量，是地面坡度的变化率，高程变化的二阶导，是坡度的坡度;总曲率是平面曲率、剖面曲率与正切曲率的和，是地表复杂度和破碎度的一种度量方式。假设z=f(x,y)是地形曲面函数，并且函数连续、二阶可导，则剖面曲率KV和平面曲率KC的计算公式如式(5—6)[14-16]所示。

(5)

(6)

式中：p是指x方向上的高程变化率；q指y方向上的高程变化率；s表示x方向高程变化在y方向的变化率；t是指y方向高程变化的变化率；r是指x方向上高程变化的变化率。

为了探求上述6种地形因子与SRTM DEM精度之间的关系，本文引入地理探测器的手段进行因子的相关性分析。地理探测器是一种新型的空间统计方法，它的基本原理继承了亚里士多德以来人类认识自然环境的主要方法。即空间分异表达，是一种能够揭示背后驱动因子的统计学方法，不同于常规的相关性分析，地理探测器具有更高的空间敏感性，能够更加直接地揭示自变量与因变量之间的关系。此方法不但能够同时参与多因子的相关性分析，并且可以揭示自变量因子间的交互影响对因变量的影响。本文中应用王劲峰等[17]开发的代码进行计算，代码下载自(http:∥www.geodetectors.org)。

2.3 分形维数的计算

本文中所采用的是表面积—尺度的方法来计算地表的分形维数,表面积—尺度法也称为投影覆盖法，由Clarke[18]等人首次提出，其主要过程如下：首先对原始SRTM DEM进行重采样，得到不同空间分辨率的数据。然后记录每一分辨率DEM的尺度Ri并且计算对应尺度下的栅格表面积Si，再利用线性拟合原理拟合lgRi与lgSi,并在双对数坐标轴上选取一段拟合度最好的一段无标度区[19]，记录下此时的拟合线性斜率K，最后由D=2-K计算得到分形维数。

在进行分维数的计算前，首先需要选择样区，在本文中共选取78个分形维数计算样区，计算样区面积大小为5 km×5 km，且样区中包含数量较多的GLA14数据点。

3 结果与分析

3.1 SRTM DEM精度评价

对SRTM DEM数据进行精度评价，做出GLA 14与SRTM DEM散点图，可以发现两者之间存在明显的线性递增关系，做出线性拟合方程，发现其斜率为1.000 9，决定系数R2为0.997 2(图1)，其拟合性极强，对其做ANOVA检验，发现其p值约为0，显著性明显。可以看出，SRTM DEM精度总体上与GLA14数据存在较为明显的相关性和一致性。图2为高程误差d的频数直方图，可以看出高程误差正值的个数明显多于负值的个数，总数上前者比后者多18.45%，为8 732个，这表明在试验样区内，多数SRTM DEM测量值较GLA14值偏大，其数据系统误差为(0.470±9.520) m，数据精度为9.531 m。

图1 GLA14与SRTM DEM拟合

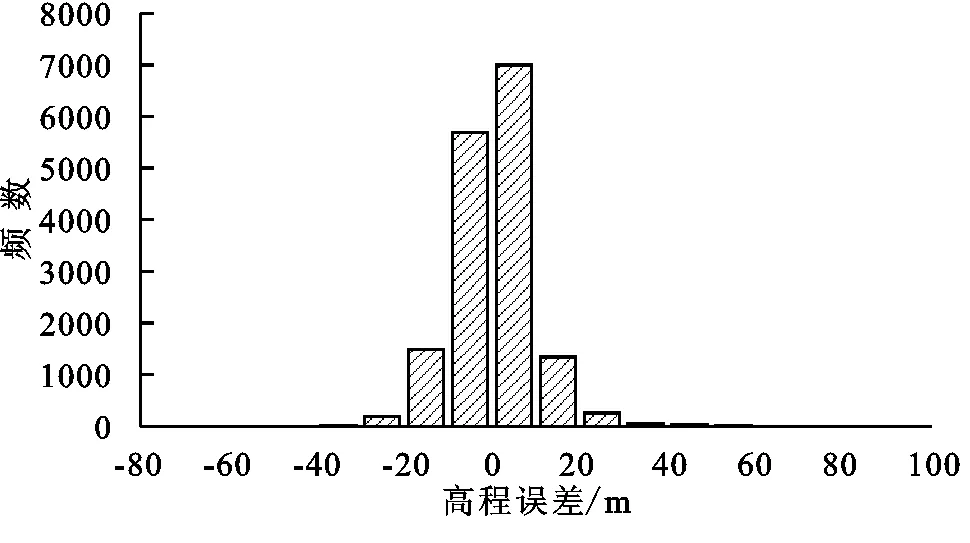
图2 高程误差频数

3.2 多因子分析

按照地理探测器的算法要求，将高程、坡度、坡向、总曲率、剖面曲率和平面曲率按照数量级进行分类。因为总曲率、剖面曲率以及平面曲率值的正负只代表该栅格表面开口的凹凸性，因此这里对三者进行绝对值处理，保证其值的大小代表了不同维度上地表的破碎程度。

设高程误差绝对值为因变量Y，高程因子为自变量X1，坡度因子为自变量X2，坡向因子为自变量X3，总曲率因子为自变量X4，剖面曲率因子为自变量X5，水平曲率因子为自变量X6，具体详情见表1。

将各地形因子分级后利用地理探测器进行解算，高程误差绝对值Y的地形因子分析结果见表2。

表1 高程误差绝对值Y各因子探测

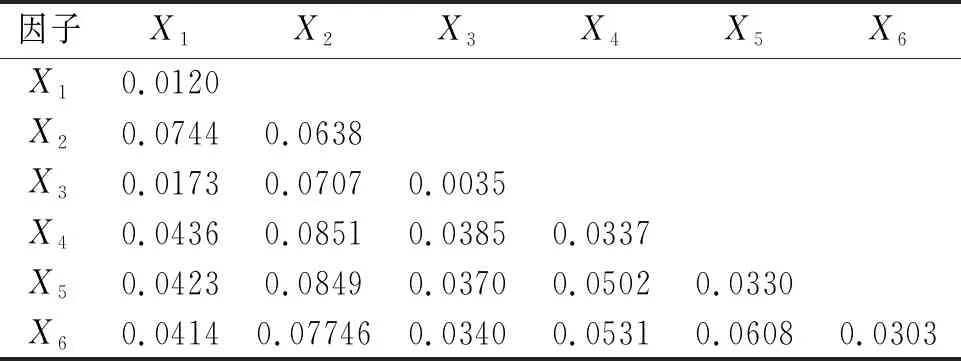
表2 高程误差绝对值Y各因子探测

在显著性水平0.05的情况下(表1)，6种地形因子皆具有显著性的统计学差异，其中坡向因子X3的q统计值最小，仅有0.003 5，这里可以认为坡向因子对高程误差绝对值的影响极小。而坡度因子X2，总曲率因子X4，剖面曲率因子X5与平面曲率因子X6的q统计值较其他因子明显较大，四者之中，坡度因子X2的q值最大，为0.063 8，说明了有6.38%的数据点高程误差绝对值Y受到坡度的影响，总曲率因子X4，剖面曲率因子X5和平面曲率因子X6的q值相当，分别是0.033 7，0 330，0.030 3，即3种因子分别解释了3.37%，3.30%和3.03%数据点的高程误差绝对值。而由表2可以看出，坡度因子与曲率因子之间的叠加以及各类曲率因子之间的叠加对高程误差绝对值的影响较大，其中总曲率因子X4与坡度因子X2的叠加和高程误差绝对值的相关性最强，q统计值为0.085 1，说明了上述两者因子的叠加解释了8.51%的数据点的高程误差绝对值Y。

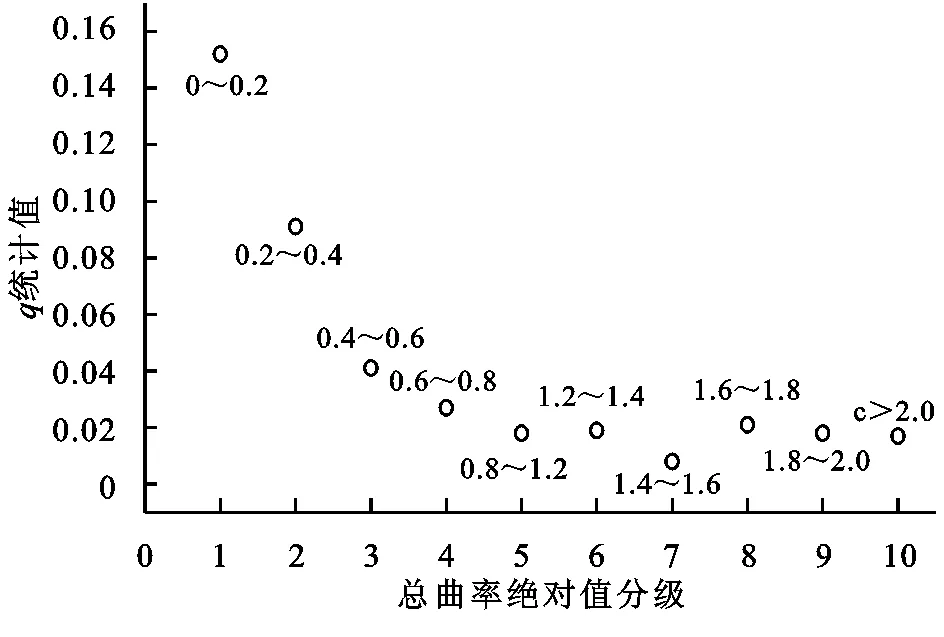
图3 坡度因子q统计值与总曲率分级关系

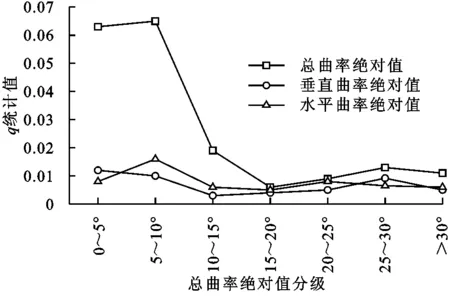
图4 3种曲率q统计值与坡度分级关系

研究发现，曲率和坡度是影响高程误差较为显著的两种地形因子。由图3可以看出，在总曲率绝对值小于0.8时，坡度因子的q统计值与总曲率绝对值呈现负相关关系，在总曲率绝对值为0～0.2时，坡度因子q统计值最大，为0.152，即坡度因子能够解释15.2%数据点的高程误差绝对值，当总曲率绝对值大于0.8时，坡度因子统计值q大致维持在0.018左右，坡度因子对高程误差绝对值的解释性较差。3种曲率因子q统计值在不同坡度分级呈现不同的分异特征(图4)，其中剖面曲率因子和平面曲率因子q统计值随坡度分级的变化，分异性不大，而总曲率因子q统计值在坡度小于10°时较大，当坡度为0°～5°和5°～10°时，总曲率因子统计值q分别为0.063，0.065，总体上，当坡度较小时，总曲率因子q统计值较大，当总曲率因子较小时，坡度因子q统计值较大。

3.3 分形维数分析

计算出每个分形维数样区内的平均误差Mean和中误差RSME，利用地理探测器进行计算，令分形维数D为自变量X，平均误差为因变量Y1，中误差为因变量Y2，结果见表3。

表3 分形维数因子探测表

在显著性水平0.05的情况下，两者的p检验值都小于0.05，具有显著性的统计学差异，分形维数与平均误差的q统计值为0.370 4，说明分维数可以解释37.04%分维数样区的平均误差，而分形维数与中误差的q统计值为0.672 6，说明分维数可以解释67.26%分维数样区的中误差。可见相比较高程、坡度、坡向、总曲率、剖面曲率与水平曲率这些普通的地形因子，SRTM DEM误差与分形维数的相关性更高。

为了进一步了解分形维数与平均误差及中误差的关系，对其进行拟合分析，结果与地理探测器的结果相一致，见图5—6，两种精度指标量均与分形维数存在明显的相关关系，相比平均误差，中误差与分形维数的相关性更强，决定系数R2达到了0.683 3。平均误差和中误差均与分形维数存在二次多项式的拟合关系，在研究区内，平均误差随着分形维数的增大先减少后增大，其平均误差最小值出现在分形维数为2.034左右，最小值约为0.260 m。中误差和分形维数的拟合趋势随着分形维数的增大，中误差呈现增大的趋势，其最大值时的分形维数约为2.046，最大值为13.42 m，在研究区内其中误差随分形维数变化处于一直增加的状态，增长逐渐趋于平稳，直到峰值。

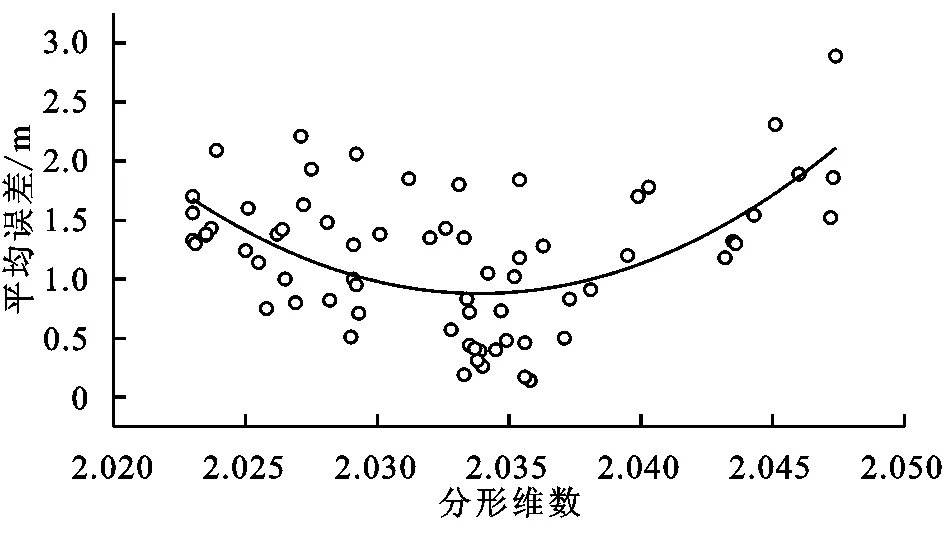
图5 平均误差与分形维数拟合

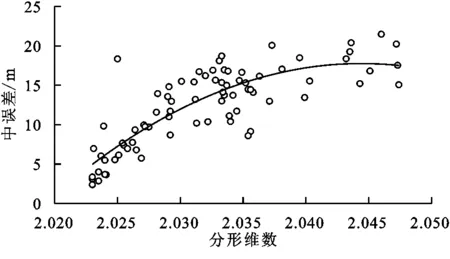
图6 中误差与分形维数拟合

4 结 论

(1) 在黄土沟壑研究区域内，SRTM DEM高程平均误差为0.470 m，高程误差标准偏差为9.520 m，数据精度为9.531 m，在研究区内符合SRTM DEM理论精度。

(2) 单一地形因子对SRTM DEM精度的影响非常小，具体来讲，高程因子、坡向因子对数据精度的影响最小，坡度因子对精度影响相对最大；地形因子两两叠加后对精度的影响较单因子变大，其中坡度因子与曲率因子综合后对精度的影响相对最大，并且当坡度较小时，总曲率因子q统计值较大，当总曲率因子较小时，坡度因子q统计值较大。

(3) 地表粗糙度(分形维数)对数据精度的影响较为明显，其作为地表自变量因子能够解释37.04%的样区的平均误差，对中误差的解释程度达到了总样区数目的67.26%。分形维数与平均误差和中误差具有比较明显的二次多项式拟合关系。