气井井筒积液高度计算模型研究

孟红霞，徐悦新，陈德春，张凯瑞，常 峰，姜 东

(1.中国石油大学(华东)石油工程学院，山东 青岛 266580；2.中国石化胜利油田分公司，山东 东营 257002)

气井积液会对气井的生产造成严重危害，导致气井产量降低或停产[1,2]，及时诊断气井是否存在积液及计算积液高度并采取适当的排水采气措施，对保证气井高效生产具有重要意义[3-6]。目前国内外学者提出了多种井筒积液高度的计算方法，如通过利用井口油套压力的差值来计算积液高度[7-9]，或通过监测气井井底流压来计算积液高度[10]，或通过测试井筒压力梯度分析井筒液面位置[11-12]，前者方法较为简单，但准确性和可靠性差，后者的花费高，不能满足目前油气田实时、智能提效的需要。笔者从气井积液规律和井筒气液分布状态出发，基于“U”型管原理和井筒流体的压力平衡，研究井筒油管与油套环空中气液两相流动机理，建立了气井井筒积液高度计算模型，利用地面实时监测参数，可以经济有效、较为准确地计算油管中积液高度和积液液面位置。

1 气井井筒积液现象

1.1 井筒积液规律

当气井产量无法达到临界携液流量时，气井将会产生积液[13]。典型井筒积液过程如图1所示，气井投产初期，地层能量充足，气体自身的能量足够将液体携带至井口，井底没有积液产生。随着气井的长时间开采，没有外来能量的补充，地层压力逐渐下降，气体自身的能量不足以将液体全部携带至井口，液体开始回落，并聚集于井底，形成井底积液。当井底存在积液时，不仅增加了气体沿井筒流动的液流阻力，而且对地层产生额外的回压，积液量太大可使气井完全停喷[14-15]。

气井井底积液主要有3个来源：一是地层中的自由水，主要包括层间水、边水和底水等；二是由于井筒流体温度和压力的降低而从天然气中凝析出的凝析液；三是外来工作液，如钻井液、压裂液等[16]。

图1 气井井筒积液过程

1.2 气井积液后井筒内气液状态

气井在正常生产不产生积液的情况下，油管内和油套环空内均无积液，油管和油套环空内会被气体所充满。

当气井产生积液后，油管和油套环空下部均会出现液体聚集，油管的上部以气液两相流动的方式生产，而油套环空的上部已存在具有一定压力的气柱；随着生产的进行，进入油套环空的气体量增加，油套环空上部的气柱不断加长，会把油套环空下部的液体顶替到井底和油管内，当油套环空气柱的长度等于管鞋深度后，油套管环空将被气体充满，自由气将不再能够进入油套环空，如图2所示。井筒为“U”型连通管，油管与油套环空在油管管鞋深度处的压力相等。

图2 气井井筒积液状态

2 井筒积液高度计算模型

根据上述气井积液后井筒内的气液分布状态，推导建立井筒积液液面深度和积液液柱高度计算模型。

2.1 假设条件

(1)气井积液产生的主要液体为水。

(2)油套环空无产量，且生产时间足够长，油套环空内为纯气体。

(3)气井采用油管稳定生产，积液井油管内的液面处以上可认为是产气较大，产液较小的稳定两相流。

2.2 计算模型

如图2所示，气井正常生产时，根据压力平衡关系，有

Ptb=Pc+ΔP1=Pt+ΔP2+ΔP3

(1)

式中，Ptb为管鞋处的压力，MPa；Pc为井口套压，MPa；Pt为井口油压，MPa；ΔP1为油套环空中气柱的压降，MPa；ΔP2为油管中从井口到积液液面处流体的压降，MPa；ΔP3为油管中从积液液面处到管鞋处液柱的压降，MPa。根据式(1)所求的Ptb，可以对积液气井的积液高度进行计算

(2)

则式(2)中h即为所求的油管中积液高度。

井口套压Pc可由井口套压表读取，沿油套环空向下根据静气柱压降计算模型可以求出管鞋处压力Ptb[17]。积液气井正常生产时，油管内下半部分为静液柱，假设气液界面距离管鞋的积液高度为h，以管鞋处压力Ptb为初值向上采用静液柱压降计算模型计算油管中液柱的压力分布(如图3中的B线)；油管内积液液面以上部分根据气体的携液能力的变化呈气、水两相流动状态，因此采用更适合计算气井压降的Hagedorn-Brown模型[18-19]，以井口油压Pt为初值向下计算油管中流体的压力分布(如图3中的A线)。直到求得井筒内积液液面上下两部分压力分布曲线的交点(图3中A线与B线的交点)，该交点对应的D-h值为井筒积液液面深度，进而计算井筒积液高度h。

图3 井筒积液高度计算

由于井筒流体的参数(如气体压缩因子和气体、液体、气液混合物密度等[20])与井筒流体的温度、压力互为函数关系，所以，需要采用迭代法求解。

3 实例计算与精度分析

根据上述井筒积液高度计算模型，利用Visual Basic语言编制相关软件，对气井井筒积液高度进行计算。

3.1 计算步骤

运用压力迭代法计算油套环空气体压力分布和管鞋处压力步骤如下：

(1)将油套环空从井口(D1,P1)到管鞋处划分成M段，取一微元段长度为Δh，并假设该段对应的压降为ΔPcl，则该段下端点压力为Pc=P1+ΔPcl；

(2)计算该段的平均压力和平均温度以及其对应的气体的压缩因子、密度等气液两相流体物性参数；

(4)重复(1)—(3)步，直到计算的ΔPc2满足精度要求为止；

(5)将D1+Δh赋予D1，将P1+ΔPc2赋予P1，重复(1)—(4)步，直到计算到管鞋处为止，此时输出油套环空中气体的压力分布和管鞋处压力Ptb。

运用压力迭代法计算油管中流体压力分布和积液高度步骤如下：

(1)将油管中从井口(D1,P1)到管鞋处划分成M段，取一微元段长度为Δh，并假设该段对应的压降为ΔPtl，则该段下端点压力为Pt2=Ptl+ΔPtl；

(2)计算该段的平均压力和平均温度以及其对应的气体的压缩因子、密度等气液两相流体物性参数；

(4)重复(1)—(3)步，直到计算的ΔPt2满足精度要求为止；

(5)将D1+Δh赋予D1，将Pt1+ΔPt2赋予Pt1，重复(1)—(4)步，直到计算到管鞋处为止，此时输出油管中从井口到管鞋无积液情况时的压力分布(如图3中的A线)。

(7)计算该段的平均压力和平均温度以及其对应的气体的压缩因子、密度等气液两相流体物性参数；

(11)求A线与B线的交点，即井筒积液液面深度D-h，从而计算出井筒积液高度h。

3.2 计算结果分析

(1)以某气田一口气井为例进行计算分析，气井的基础数据如表1所示：

根据气井井筒温度分布方法[21]，计算得到该井温度剖面如图4：

表1 某气井基础数据

图4 计算实例温度剖面

根据环空纯气柱压力计算模型，由套管压力计算油套环空油管管鞋处压力为20.035 MPa，并以此压力向上计算液柱压力分布(如图5中B线所示)，与从井口压力向下计算的油管内流体压力分布(如图5中A线所示)交于一点。

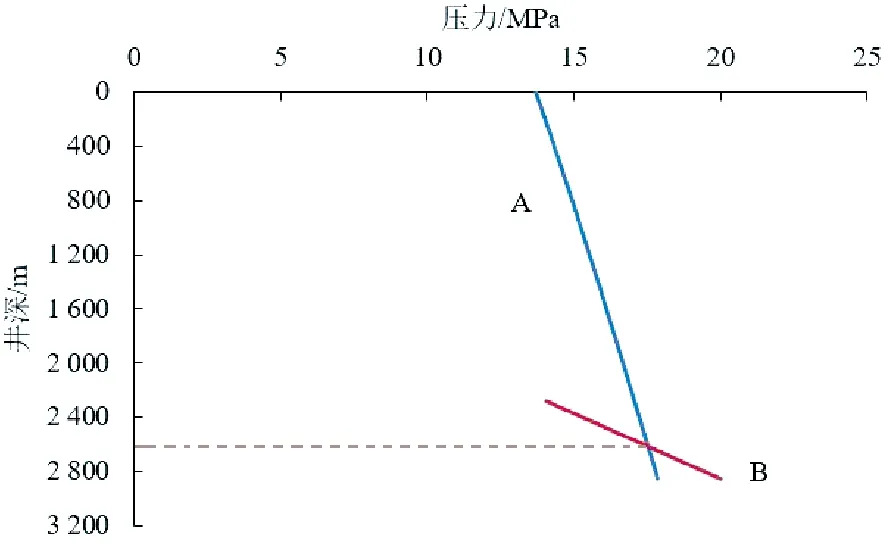
图5 计算实例井筒压力分布

如图5所示，虚线处即为积液深度2 633.3 m处，从而求得积液高度为237 m，而实际测得积液高度为240.1 m，相对误差为1.3%，表明所建立的模型具有较高的精度。

(2)以下采用某气田的气井生产数据(见表2)，对模型进行检验，计算结果精度分析见表3。

表2 某气田生产数据表

计算结果见表3，表明在气井基础数据确定的情况下，只需测得井口油压、井口套压等参数，就可以较为准确地计算出气井井筒中的积液高度和积液液面深度；10口井的井筒积液高度平均绝对误差为39.67 m；平均相对误差为12.71%。积液液面深度的平均绝对误差为39.67 m，其中3号井和7号井误差较大，平均相对误差分别为6.66%和6.01%，平均绝对误差分别为-153 m和-57 m。各井积液液面深度的平均相对误差为2.02%，能够满足工程计算的需要，表明所建立的模型具有较高的精度。

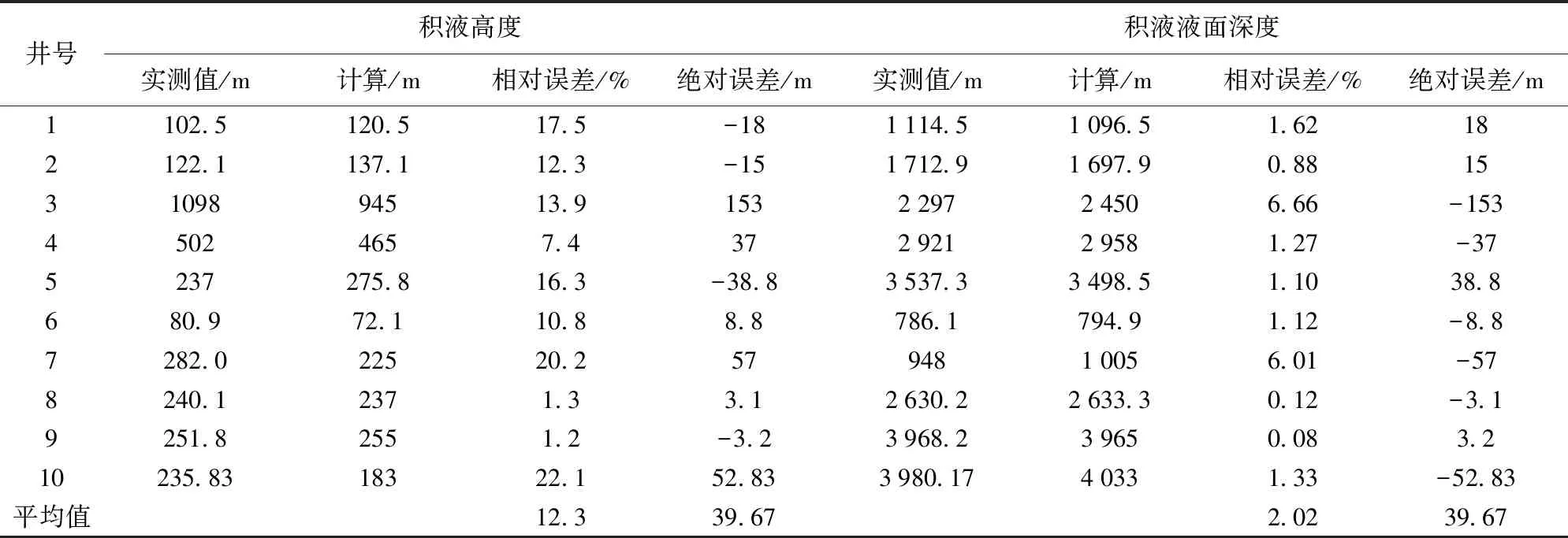
表3 计算结果精度分析

4 结论

(1)针对目前国内外计算积液高度的方法较为单一、准确性低、经济效益差、不能满足智能化、信息化需要等问题，建立了气井井筒积液高度计算模型，利用地面实时监测参数，可以经济、定量、较为准确地计算油管中积液高度和积液液面深度。

(2)现场10口井例计算结果表明，所建立的气井井筒积液高度计算模型的计算值能够满足工程计算的需要，为生产措施设计与实施提供依据。