边坡渗流与坡面径流联合求解三维有限元模型

王乐，田东方

(三峡大学水利与环境学院，湖北宜昌443002)

降雨特别是强降雨常常诱发边坡失稳，王一超[23]等就降雨诱发土质边坡失稳的成因进行了相关研究。由于边坡岩土体的强度和受力等均与渗流场相关，因而强降雨时边坡水分运移模拟是准确评价边坡稳定性的基础。但在强降雨条件下，除降雨入渗过程外，往往还伴随坡面径流；入渗与径流过程相互影响，使问题变得十分复杂。

降雨时边坡渗流模拟可基于Richards方程[1]实现。目前的各种分析方法中，在坡面未产流之前，将坡面视为流量边界，流量大小即为降雨强度；坡面产流之后，根据对坡面径流处理方式的不同，可以分为2类。

a) 忽略坡面径流，将降雨入渗边界视为定水头边界，水头值等于地面高程[2-7]。这类方法的依据是:虽然坡面径流增加了入渗水头进而增大入渗率，但坡面水深往往很小，忽略这一水深(即认为水深为0)对入渗率影响不大。

b) 考虑坡面径流，如采用运动波方程[8]或扩散波方程[9]描述坡面径流，与渗流场耦合求解。根据耦合方式的不同，又可细分为2种方法。①以坡体渗流、坡面径流两场间的交换流量为联系，采用迭代方法求解。基本思路是先假定两场在坡面的交换流量，以此为边界分别求解两场，然后根据计算结果基于达西定律更新交换流量后再求解两场，如此循环计算；以前后2次计算所得径流水深是否足够接近为依据结束迭代[10-14]，这种方法可称为迭代求解模型。②同样以两场间的交换流量为联系，通过消去交换流量这一未知量，将渗流和径流两场同时求解；例如用径流水深表示交换流量，然后代入渗流场边界条件[15]，又如把离散后的两场方程组(例如有限元格式的离散方程组)相加消去交换流量[16-17]；这种方法可称为联合求解模型。该方法要求在离散两场控制方程时，对时间和空间的离散必须相同(详见本文第3节)。

上述方法在处理某些特定问题时存在一定缺陷。以图1为例，当滑床渗透性较小而滑体渗透性较大，在强降雨条件下边坡AB段产流但BC段未产流，虽然AB段边坡的径流水深对该段边坡降雨入渗影响较小，但雨水会流经至BC段边坡而入渗。与坡面水深对渗流的影响相对应，本文将径流的这种影响称之为流量补给。第一类方法无法考虑该影响[18]；文献[19]通过修正流量边界，建立了可以考虑流量补给的二维联合求解模型。然而产汇流受地形影响较大，二维方法无法模拟三维情形下的产汇流过程。因此，本文在文献[19]的基础上开展进一步研究，建立了三维联合求解模型。

图1 典型滑坡剖面

1 基本理论

1.1 非饱和渗流控制方程

以各向同性和忽略源汇项的多孔介质饱和-非饱和渗流为例，基于质量守恒和达西定律的Richards方程[1]为：

(1)

式中C=∂θ/∂hs——容水度，L-1，这里表示非饱和土的容水度；θ——体积含水率；hs——压力水头，L；H=z+hs——总水头，L；z——位置水头，L；t——时间，T；K=KrKs——渗透系数，L/T；Kr——相对渗透系数；Ks——饱和渗透系数，L/T；x、y、z——空间坐标，L，z轴竖直向上为正。这里L、T分别表示长度、时间量纲。

初始条件为：

H(x,y,z,0)=H0(x,y,z)

(2)

简单起见，边界条件只考虑降雨入渗边界S：

在未产流边界S1上：

(3)

在产流边界S2上：

(4)

式中H0——已知函数；R——降雨强度，L/T；nb——坡表内法线方向；I——入渗率，L/T；S=S1∪S2；S1∩S2=空集。

1.2 坡面径流控制方程

采用运动波模型描述坡面径流，该模型已被证实可用于模拟浅水和缓坡时的径流过程[15]：

(5)

式中h——垂直于坡面方向的水深，L；x'、y'——位于坡面的坐标系；qn=Rcos(nb,z)-I——净雨率，L/T；qsx'、qsy'——x'、y'方向的单宽流量，L2/T，由式(6)计算：

qsx'=C1h5/3；qsy'=C2h5/3

(6)

通常可认为初始时刻坡面无径流；边界条件为径流上游边界(分水岭处)水深一直为0。

1.3 VG模型

非饱和渗流方程中的容水度C和相对渗透系数Kr可由土水特征曲线(SWCC)确定，常用的有VG模型：

(7)

(8)

式中Se——有效饱和度；θr——残余体积含水率；θs——饱和体积含水率；a——VG模型拟合参数，L-1；n——VG模型拟合参数，m=1-1/n。

2 联合求解模型的构建

2.1 求解域的离散

本文采用有限元离散渗流控制方程；采用特征有限元离散坡面径流控制方程。只对渗流计算域划分网格；径流计算网格用渗流网格的坡表部分；两场采用相同的空间离散。以图2所示的一个单元为例，渗流网格单元为12 345 678，则径流网格单元为1 234。同时，两场也采用相同的时间离散。当坡面产流后，由于坡度较缓，垂直水深近似等于竖直水深，即式(1)中的hs近似等于式(5)中的h。因此，渗流场中坡表节点与径流场中相同位置的节点在同一时刻具有相同水深，例如节点1、2、3、4等。

图2 有限元网格

2.2 控制方程的FEM格式

Richards方程的有限元格式为：

(9)

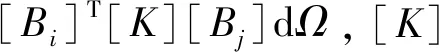
运动波方程的特征有限元离散格式推导如下。式(6)可写成：

(10)

(11)

式(11)变为：

(12)

设tk是时间的第k层，h=∑Nihi。式(12)的加权余量格式为：

(13)

ψ(x',y',tk)·

(14)

(15)

将式(14) 、 (15) 代入式(13) 并写成矩阵形式：

(16)

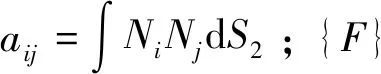
2.3 联合求解FEM模型的构建

由于H=hs+z，而hs近似等于h，则式(16)可写成：

(17)

将式(9)、(17)等号两边对应相加：

(18)

进一步化简为：

(19)

式(19)即为联合求解模型的有限元格式。矩阵[A]只在产流的坡表单元上才不为0。

(20)

2.4 流量修正

坡面被离散为四边形单元，见图3。用h1、h2、h4、h5、h7和h8分别表示节点1、2、4、5、7和 8的水深。假设此时h1和h2为负值，而h4、h5、h7和h8为正；即单元I产流，而单元II未产流。此时，对单元II而言，边界入渗流量将包括降雨、邻近产流单元的径流补给两部分(如单元I)。此处以单元I为例说明径流补给流量的确定方法。

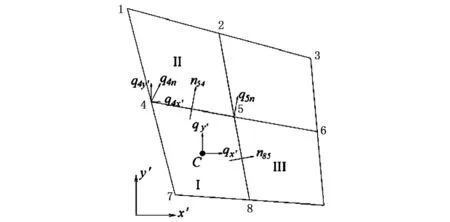
图3 补给流量的确定

首先根据节点水深由式(6)确定节点流量。例如节点4沿x'方向、y'方向流量，分别用q4x'和q4y'表示；节点5的2个流量分量也可同样确定。则单元I经边45流向单元II的水量随之确定。单元II的其他临近的产流单元也类似确定补给流量，设单元II的总补给流量为Qa，则单位面积补给流量为qa按式(21)计算：

qa=Qa/SII

(21)

式中SII——单元II的水平投影面积,L2。

计算时，每个时步内先通过式(19)计算渗流和径流场，然后根据径流结果按2.4节方法计算补给流量修正边界条件后再次计算，直到前后两次结果充分接近后再进入下一时步。

3 数值算例

以简单边坡为例，从累积入渗量的角度，说明当边坡渗透性差异较大时，使用本文方法的必要性。计算域为平行六面体ACFDGINL，见图4。ACFD为降雨边界，降雨强度为R= 20 mm/h，持续10 h；其余为不透水边界。初始体积含水率θ0为0.1。区域ABEDGHML为材料1；区域BCFEHINM为材料2。材料2的SWCC和渗透性函数数据见表1，饱和渗透系数用Ks2表示。简便起见，材料1的饱和渗透系数为7.22×10-7cm/s，其余与材料2相同。

图4 算例的几何尺寸(cm)

表1 SWCC 与渗透性函数

分别采用本文方法和Geo-Seep模拟了不同Ks2时的降雨入渗过程。图5为2种方法所得的累积入渗量(Q1、Q2)以及与累积降雨量RC的相对误差(D1、D2)。其中，Q1、D1为本文方法结果；Q2、D2为Geo-Seep结果。

a) R=20 mm/h,Ks2=10-4 cm/s

b) R=20 mm/h,Ks2=10-3 cm/s图5 累积入渗量对比

图5a表明，当下段边坡渗透系数Ks2相对雨强较小时，不仅ABED段边坡很快产流，而且BCFE段也很快产流，径流对渗流的影响只有径流水深，2种方法结果几乎相同；说明了此时如果只关心入渗过程，忽略径流是合理的。图5b表明，当渗透系数Ks2相对雨强较大时，只有ABED段边坡很快产流，而BCFE段未产流，径流对渗流的影响除了径流水深还有流量补给，本文方法更符合实际情况。此时如不考虑径流补给，累积入渗量则只有累积降雨量的一半左右；可以推知，随着产流区域(ABED)面积的进一步增大，误差将更大。

4 结论与展望

a) 采用Richards方程描述边坡饱和-非饱和渗流过程，采用运动波模型描述坡面径流过程；分别采用有限元和特征有限元格式构建渗流、径流控制方程的有限元格式；将2组有限元方程相加而消去交换流量，构建了边坡渗流与坡面径流联合求解模型；根据径流场修正入渗边界流量。

b) 采用所建模型和Geo-Seep对简单边坡降雨入渗进行数值模拟，累积入渗量的对比表明：当上段边坡渗透性相对下段边坡较小，且上段边坡产流而下段边坡未产流时，本文方法所得的累积入渗量更加符合实际情况。