基于MATLAB的电力系统潮流仿真与研究
2019-05-20罗金鸣杨奥博
刘 哲,高 兢,宫 婷,罗金鸣,杨奥博
(1.沈阳工程学院a.电力学院;b.自动化学院,辽宁 沈阳 110136;2.华北电力大学电力工程系,河北 保定 071003)
随着社会的不断发展进步,整个社会对电力的需求越来越多。在现代社会,电力已经成为人们生活中必不可少的一部分。因此,对电力系统的安全性和可靠性要求也越来越高。一个小规模的电力系统网络故障可能会造成电网系统大面积的停电事故,这类事故会给经济发展和社会稳定造成巨大损失,而且电力系统相关的实验具有较高危险性。因此,对电力系统进行仿真,这对电力系统的运营与规划具有重要意义。采用仿真这种方式可以有效地对电力系统各类安全事故进行提前判断,进一步减少电力系统运行风险。因此,研究人员为提高电力资源分配合理性和电力系统安全性,对电力系统进行了大量的仿真与计算[1-3]。
在电力系统仿真与计算中,潮流计算是电力系统规划中最重要的分析手段之一。其主要目的是对电力系统在各种运行方式下的运行状态进行估计与测量,可以全面、正确地掌握电力系统中各元件的运行状态,确定合理供电方案[4-5]。基于牛拉法潮流计算的基本原理,利用MATLAB软件,对基于IEEE三机9节点模型开展潮流计算工作,如图1所示,通过结果对比验证所述计算方法的可行性。
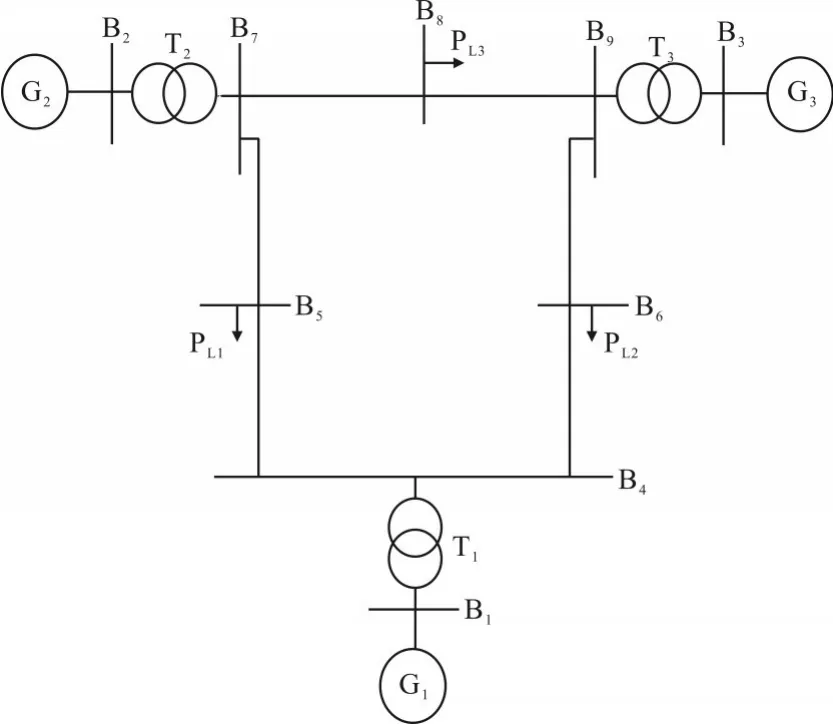
图1 IEEE三机9节点电力系统网络
1 潮流计算方法简介
1.1 模型选择
电力系统是包含发电机、变压器、串并联补偿等设备的复杂系统,为了对系统整体进行准确的计算,需要根据系统内各元件物理特性和电磁特性选择合适且易于进行计算的数学模型[6]。在选择适合计算的各元件模型后,即可确定三机9节点网络的基本电路模型。
在稳态潮流计算中,一般认为系统的三相是对称的,故以单相的等值电路模式表示此三相电力系统。鉴于本网络所给数据,该系统使用π型等效电路来代表架空线路。由于该系统具有多个电压等级,为方便准确地进行对网络中相关参数和变量归算,以π型等效电路代表变压器进行仿真和计算。
电力系统的网络方程式指的是可以用于反应网络性能的数学方程式组,该方程组主要由与网络本身有关的参数、变量,以及参数与变量之间相互作用关系归纳得出。运用牛拉法对系统进行潮流计算仿真模拟,在选择模型后,需列出关于本网络参数与变量及网络功率方程。网络方程式一般是由相应的节点导纳矩阵或节点阻抗矩阵所描述产生。在对较多节点的电力网络进行分析时,由于电力系统网络导纳矩阵具有良好的稀疏性与对称性,占用内存空间较小,可以较为高效快捷地处理电力系统网络方程,故选用节点导纳矩阵表示网络中的各个参数[7-8]。
1.2 牛拉法基本原理与步骤
牛顿拉夫逊法是在数学上求解线性方程组的有效方法,其主要原理是将非线性方程组化为对应的线性方程组,然后对线性方程组求解。在数学中,此类非线性方程转化并求解的方法被称为线性化方法。实际求解的主要过程为将非线性方程组(f(x)=0)在某个待求量x的初始数值附近估计值x0,在此估计值x0附近进行泰勒展开,在展开项中一般忽略二阶及二阶以上的高次项,化简并列出相应公式,则可得到一组由原式线性化后得出的方程组,这类方程组一般被称为修正方程组,其简写为

式中,Δx为变量修正值;J为雅克比矩阵;Δf为修正量。
运用牛拉法进行潮流计算时,初值要选择比较接近于精确解的值,否则在迭代的过程中可能发生不收敛的情况。牛拉法在求解电力系统潮流功率方程中一般可直接使用,可解得:
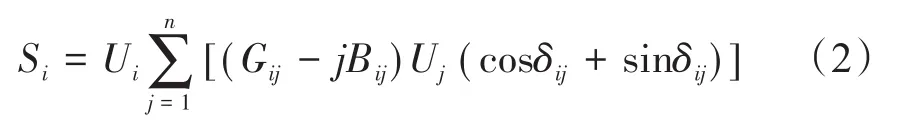
式中,S为节点功率;U为节点电压幅值;δ为节点电压相角;G、B为线路导纳。
使用牛拉法的关键问题在于构建修正方程组并进行求解。因此,对网络中各个节点进行编号,将其中电压与相位角已知的节点作为平衡节点,建立关于牛拉法的直角坐标修正方程。计算的基本步骤如下:
1)列出由所给参数决定的节点导纳矩阵,带入PV节点和平衡节点所给定的电压初始值,假设PQ节点的电压初始值;
2)将节点电压的初始给定值和假设值均带入到修正方程中,求出方程组中的不平衡量并记录;
3)求雅克比矩阵各元素,即对各节点功率、电压求对电压的偏导数;
4)解修正方程组,求出各节点的变化量;
5)计算各节点修正后的具体数值,并将此数值带入下一步的迭代计算;
6)迭代至修正量满足收敛条件,并计算平衡节点和各条线路上的潮流分布[9]。
2 潮流计算仿真分析过程
2.1 节点导纳矩阵建立
先输入各支路情况,再通过MATLAB编程将三机9节点网络中的变压器模型变换为π型等效电路,免去不同电压等级的归算。因此,先输入支路数量、系统中节点数目、各个节点编号以及本次实验的误差精度等参数。
导纳矩阵的基本形式为任意节点i的自导纳为在变压器改为π型等值电路后,与其所连的各个支路上的导纳之和。若支路上不存在变压器,则在此回路上,该节点导纳为此支路阻抗倒数与靠近节点侧的电纳之和。若两节点间存在变压器,需先判断该节点在变压器π型等值电路中位于高压或低压侧,然后确定此节点在变压器所在支路上的导纳大小。因此,在此支路上的该节点导纳相较于不存在变压器时,增加了变压器等值电路带来的导纳大小。I节点自导纳为i节点与各个支路导纳之和,在程序中采取累加的形式;节点i,j两点间互导纳为阻抗倒数的相反数,如有变压器只需加上导纳与变比的比值。在程序中,对于节点i,j从1至9循环重复上述步骤,建立n阶对称的导纳矩阵。
2.2 节点电压设置
平衡节点的电压值和相位角度按照给定的初始数值设定,PV节点的电压值也按照三机9节点系统初始值给定,但PV节点的节点电压和相位角未由此系统给定,平衡节点的节点电压和相位角均为此系统的给定初始值。在一般小型三机9节点电力系统中,节点之间电压差较小,相位角度较为接近。在初次迭代过程中,设PV节点的相位角为0°,设PQ节点的电压大小和相位角初始值为V=1.00+j0。平衡节点电压值、相位角度和PV节点电压值按照给定值输入程序中。
2.3 不平衡量求解
牛拉法计算的核心就是修正方程组的建立和求解。首先,应将前面假设的量(如PQ节点的电压值和相位角,PV节点的相位角)带入不平衡量求解公式中;然后,由此可以计算出PQ节点有功和无功不平衡量及PV节点的有功功率和节点电压平方的不平衡量[10]。
求出的3个不平衡量为初次计算的不平衡量,将其列为2(n-1)行的列向量,即为修正方程组等号左侧的列向量。
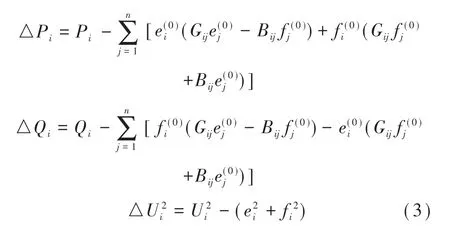
式中,P、Q分别为节点的有功功率和无功功率;e、f分别为用直角坐标表示的节点电压实部和虚部的初值;G、B为线路导纳。
2.4 雅克比矩阵
在以一般牛拉法为基础的潮流计算方法中,进行计算电力系统潮流分布时,每迭代一次,都需要对雅克比矩阵进行重新计算并对其进行求逆工作。雅克比矩阵元素求法如式(3)所示,由对有功功率、无功功率和电压平方3类量求其对电压实部与虚部的偏导数得出[11]。
在MATLAB中要实现求解雅克比矩阵,则首先需要考虑到判断节点,以此可以判断雅克比矩阵中相应元素的位置。在确定节点类型后,分主对角线元素(即i=j时)与非对角线元素两种情况,用if判断语句和for循环,进行初次形成的雅克比矩阵工作。由于此雅克比矩阵中不包含平衡节点,故在三机9节点系统的修正方程中,雅克比矩阵的阶数为16阶,即2(n-1)阶。
3 潮流计算仿真运行及结果
通过程序将雅克比矩阵求出后,将数值带入修正方程中。首先,对雅克比矩阵求逆(因雅克比矩阵值不为零,则此矩阵必可逆),两侧同时乘以雅克比矩阵的逆;然后,可求得各个节点的节点电压修正量,如修正量不满足精度要求,则先算出各节点电压的新值,带入式(3)中,重新开始上述迭代,迭代至修正量满足小于给定精度的条件后,停止迭代,得出结果即为节点电压数值的最终值;最后,再计算三机9节点系统中各个支路的潮流分布情况,如图2和图3所示。

图2 节点电压分布

图3 各节点相位角变化
4 潮流计算仿真结果验证分析
MATPOWER中仿真数据如图4所示,计算结果如图5所示,与2.4节MATLAB程序得出结果相比误差在千分之一以内,可以基本认为符合电力系统潮流计算的要求。上述方法计算所得各节点电压与MATPOWER计算结果基本一致,计算参数如表1所示,计算结果如表2所示。经过对比和研究发现,各支路潮流分布略有差距,主要由所需收敛精度不同导致。
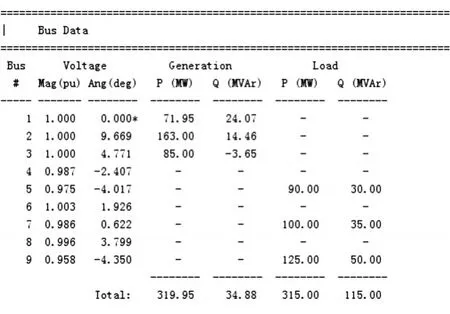
图4 MATPOWER三机9节点系统基本数据
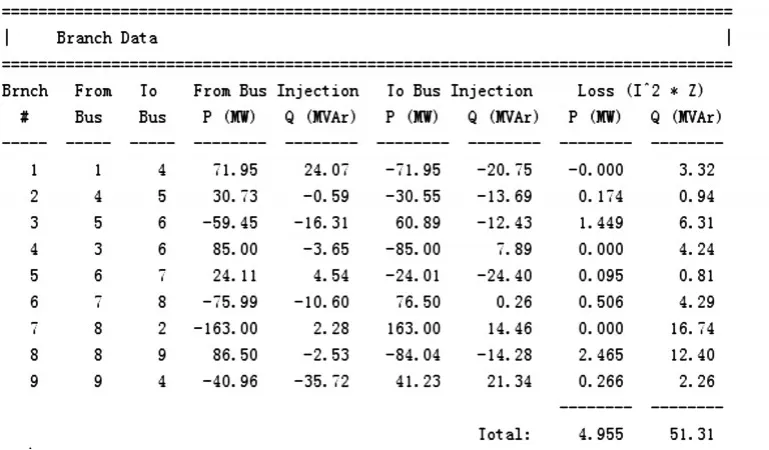
图5 MATPOWER三机9节点系统各个分支潮流

表1 IEEE三机9节点各节点电压分布
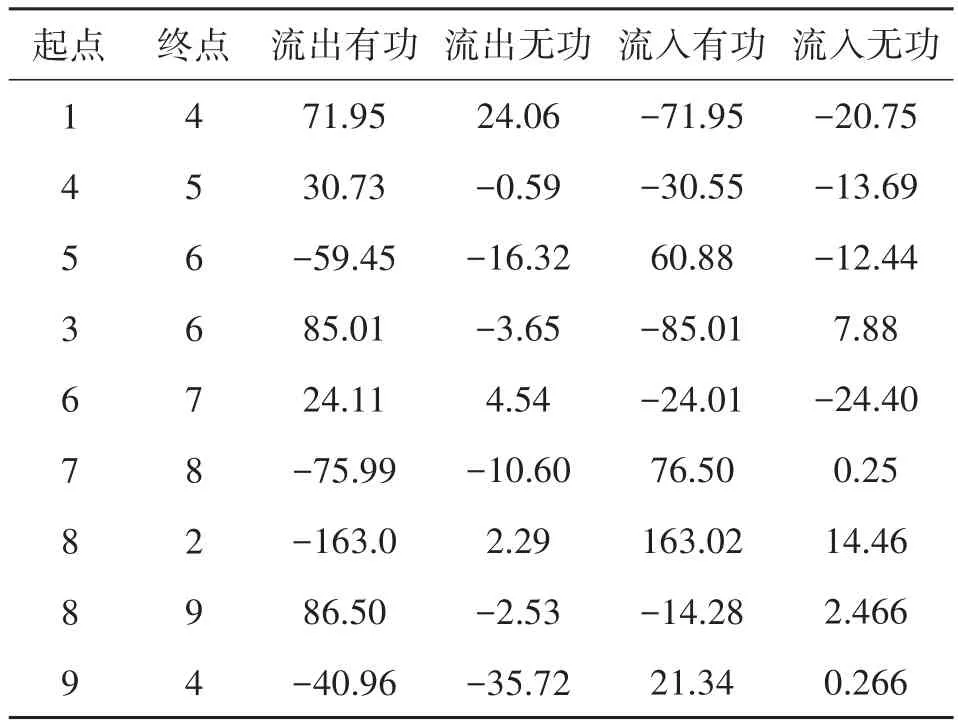
表2 IEEE三机九节点系统各支路潮流分布
5 结 论
以三机9节点系统潮流计算建模与仿真验证为主题,简要介绍了复杂电力系统潮流的计算机算法类别和基本原理,并详细说明了电力系统潮流计算基本步骤,对此系统进行计算和仿真验证。通过编写程序计算结果与专业软件计算结果的对比,验证了所提出计算仿真方法的可行性。
1)确定循环重复迭代是本次计算机潮流计算的核心算法。对节点按序逐个进行输入,通过形成节点导纳矩阵,为功率方程求解做准备。在此过程中本算法可以直接将变压器模型转换为π型等效电路,不需提前进行图形变化,对计算机潮流算法进行了简化和优化。
2)运用MATLAB中所自带的MATPOWER程序对系统进行潮流计算,计算出各个节点的节点电压和各支路潮流分布情况,进而表述出系统运行状况。通过编写牛拉法潮流计算算法与MATPOWER程序计算结果进行对比分析,两种算法结果差值在规定误差以内,证明了本文所述方法对三机9节点系统进行潮流计算的可行性。
