钢框架外环板式节点力学性能变参数分析

陈 颢

(昆明有色冶金设计研究院股份公司，云南 昆明 650000)

0 引 言

钢框架结构广泛运用于现今的建筑业中，钢框架结构相对于钢筋混凝土框架结构而言，自重小，材质均匀，能以较小的构件断面，获得更大的跨度空间。钢框架结构中，框架节点连接上、下框架柱，水平连接框架梁，传导所连接构件的弯矩、剪力、轴力，节点处受力复杂，特别是圆形钢管柱类型的钢框架节点，由于柱截面为圆形的特殊性，节点的受力情况更为复杂。本文分析对象为圆钢管柱式钢框架节点，节点加强方式采用外环板加强方式，节点两端钢梁为H型钢且梁高不同。对该钢框架节点(后文简称为节点)的力学性能研究，有利于更清晰的了解钢框架节点在竖向荷载作用下的受力状态，对钢框架结构的设计和运用具有促进作用。

1 节点力学性能定义

节点的力学性能指：节点的梁端在竖向荷载作用下，梁端的屈服位移(Δy)、屈服荷载(Py)、极限位移(Δu)、极限荷载(Pu)。屈服位移和屈服荷载指在荷载作用下，节点最大应力处达到材料屈服强度(fy)时的梁端位移量和梁端作用荷载；极限位移和极限荷载指钢框架节点最大应力处达到材料强度(fu)时的梁端位移和梁端作用荷载。

2 节点力学性能变参数分析概述

节点力学性能分析一般指根据研究目标，通过现场加工钢构件并进行现场试验所取得的节点试验数据，对节点性能进行分析。本文采用数值分析法对节点的力学性能进行分析，数值分析软件为有限元分析软件ABAQUS。分析步骤为：①确定有限元分析模型(后文简称模型)几何参数和分析参数，建立模型，模型几何参数含节点各部分截面尺寸和构件长度，分析参数指节点材料本构关系、单元划分、边界条件等；②依据分析目标，确定模型的加载方式、加载位置和荷载大小，将荷载按加载顺序至模型，并进行分析；③对模型分析数据提取、整理；④得出分析结果。该文变参数分析为改变节点的3个几何参数：轴压比、管壁厚、外环板厚度，对节点分别建立模型并分析。该文分析目标即为3个几何参数的变化，对节点梁端的屈服位移、屈服荷载、极限位移、极限荷载及P-Δ曲线的影响。

3 节点有限元模型建立及加载

节点模型构件截面参数见表1。

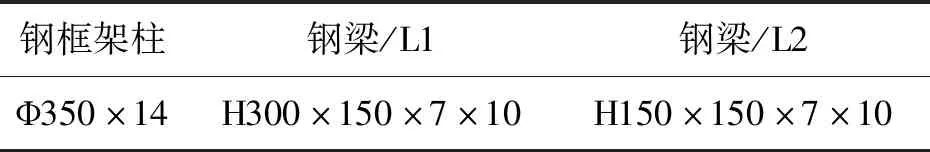
表1节点构件几何截面参数表Tab.1 Table of geometrical section parameters of joint members

钢框架节点大样见图1-3。

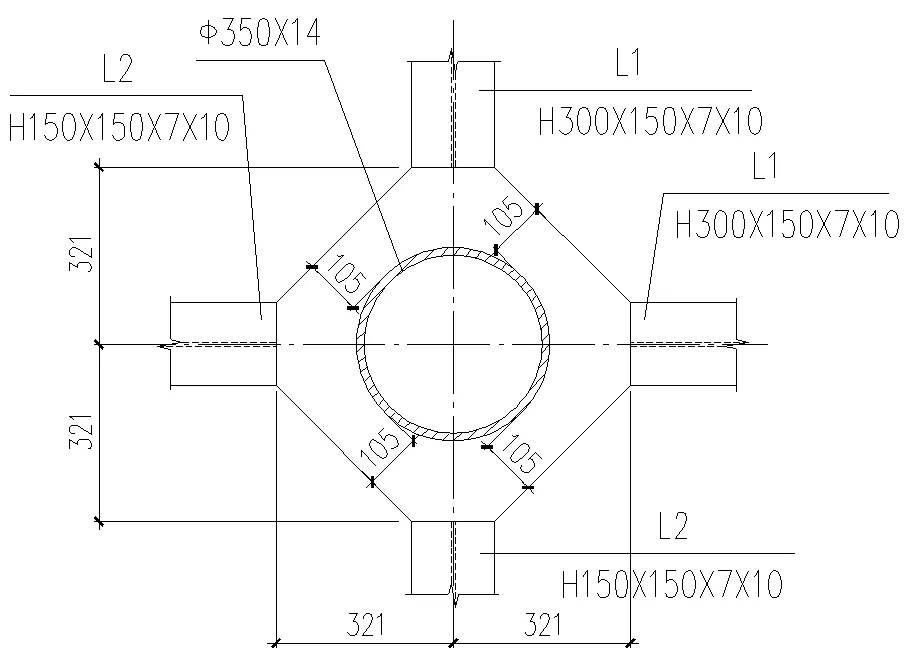
图1 外环板上翼缘Fig.1 Flange on outer ring plate

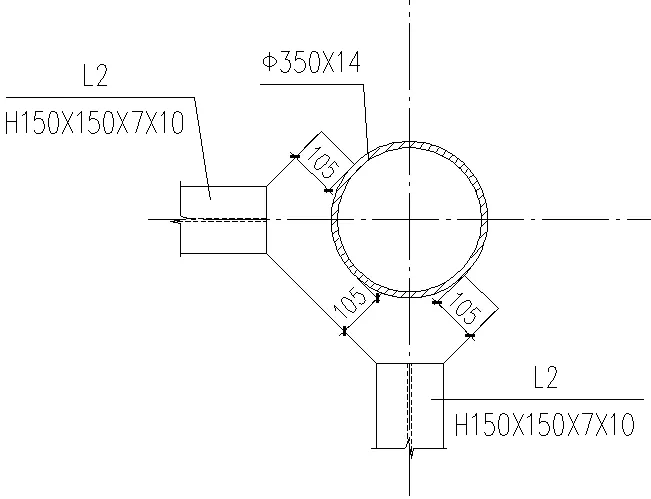
图2 H150×150×7×10钢梁外环板下翼缘Fig.2 Lower flange of H150 × 150 × 7 × 10 steel beam outer ring plate

图3 H300×150×7×10钢梁外环板下翼缘Fig.3 Lower flange of H300 × 150 × 7 × 10 steel beam outer ring plate

钢框架层高取为3 000 mm，且反弯点均处于层高中部，柱距为3 000 mm，钢梁最大弯矩处于跨中。

模型材质考虑为Q345钢材，材料本构关系见表2。

表2 材料本构关系表Tab.2 Material constitutive relation

材料弹性模量E=2.1×105 N/mm2，泊松比μ=0.28。该文主要为钢框架节点力学性能的变化规律性分析，故考虑材料为BKIN理想弹塑性材料，梁端P-Δ曲线无明显下降段，单元达到最大应力500 MPa，即认为单元破坏；材料屈服准则为米塞斯准则，材料流动法则为法向流动法则。节点分析模型的单元划分为壳单元(S4R)，沿壳体厚度方向设置5层分析层；网络划分采用自由网络划分，为能够较精确的分析节点，同时兼顾分析效率，节点部位采用加密种子布置，取种子间距为15，节点以外的框架柱和钢梁取种子间距45和60。节点模型见图4，节点单元划分见图5。

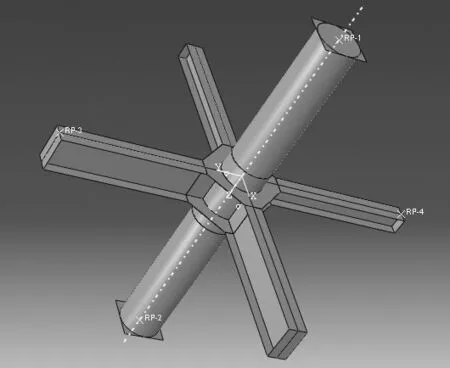
图4 节点模型Fig.4 Node model

图5 节点单元划分Fig.5 Node unit division

节点模型边界条件设置为：柱顶铰接，不限制轴向位移，柱底铰接，限值轴向位移为零，钢梁上翼缘均限值钢梁平面外位移。

节点模型加载分为：①钢框架柱轴压比加载，除节点轴压比分析外，均取轴压比为0.3；②梁端加载，加载方式为单调加载，荷载大小为1.2倍的钢梁极限荷载；梁端加载见表3，节点模型加载示意图，见图6。

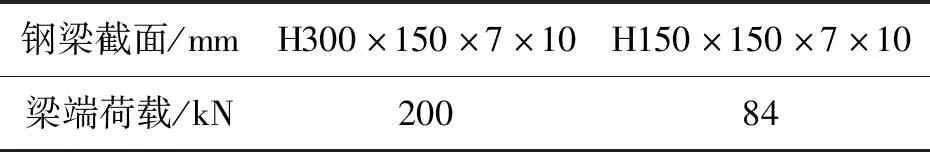
表3 梁端加载表Tab.3 Beam end loading table

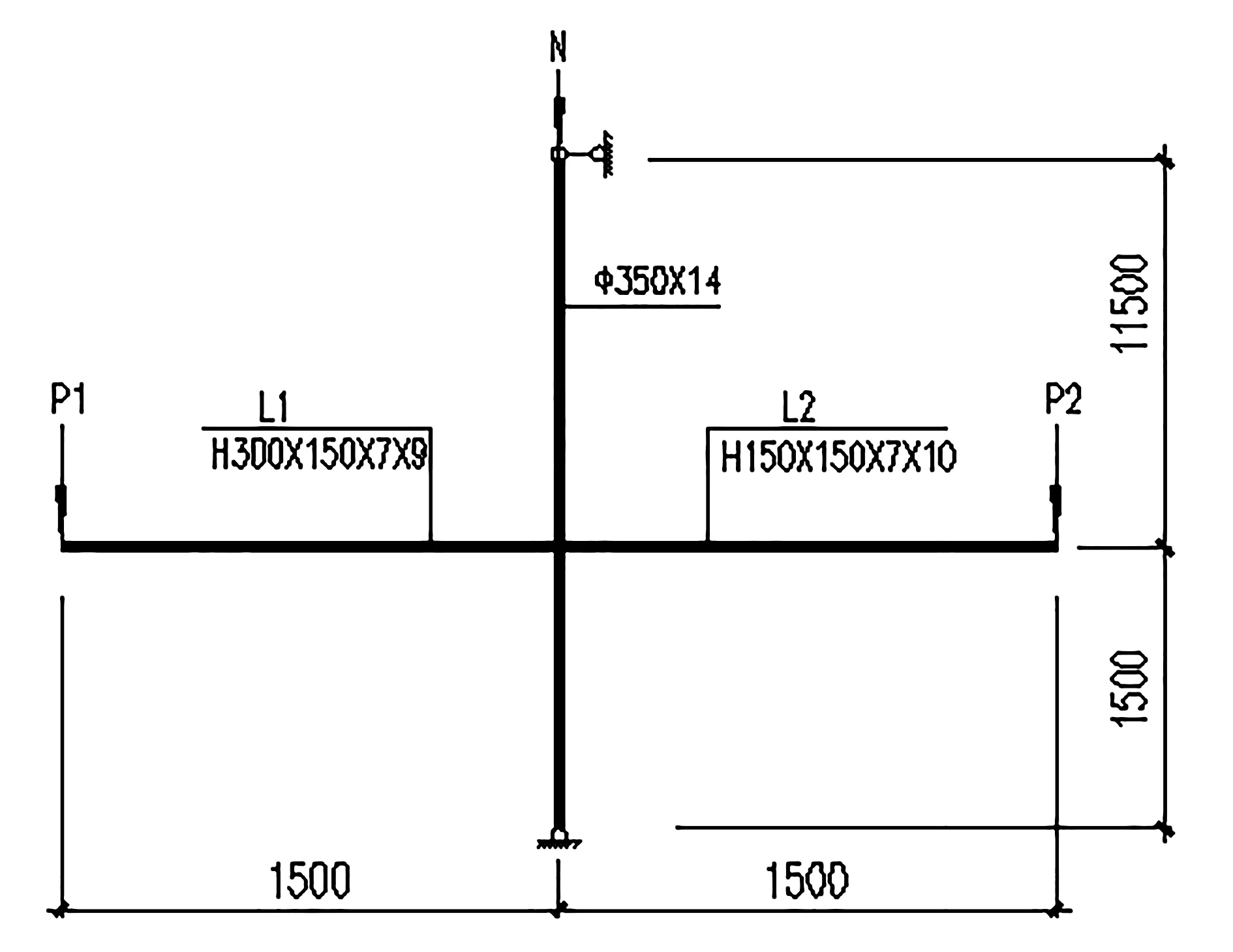
图6 节点模型加载示意图Fig.6 Schematic diagram of node model loading

4 变参数分析几何参数设计

1)不同轴压比对节点力学性能影响分析模型节点编号及柱顶荷载见表4。

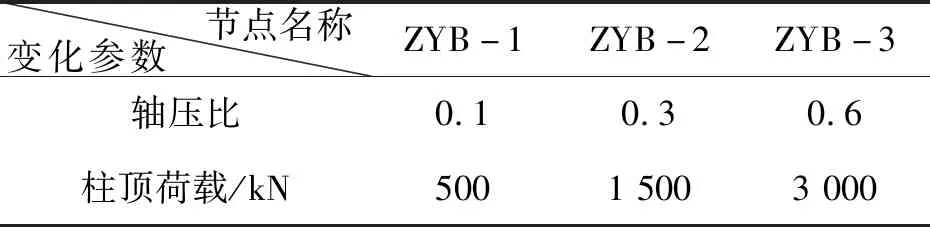
表4 轴压比和柱顶荷载表Tab.4 Axial compression ratio and column top load table

注：其余节点轴压比均为0.3。表中节点名称即为本组三个节点的名称，后文均按此方法设定。

2)不同管壁厚对节点力学性能影响分析模型节点编号及柱顶荷载，见表5。

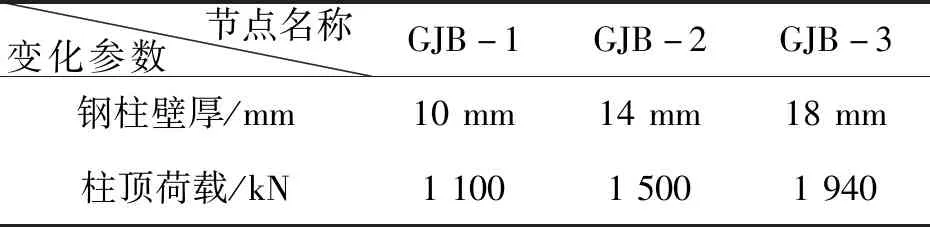
表5 管壁厚和柱顶荷载表

3)不同外环板厚度对节点力学性能影响分析模型节点编号及外环板厚度见表6；

表6 外环板厚度表Tab.6 Outer ring plate thickness

5 节点模型分析及数据整理

综上所述，建立模型并分析，取得分析数据后整理如下：

1)不同轴压比对节点力学性能影响分析结果，见表7，梁端P-Δ曲线对比图见图7，图8。

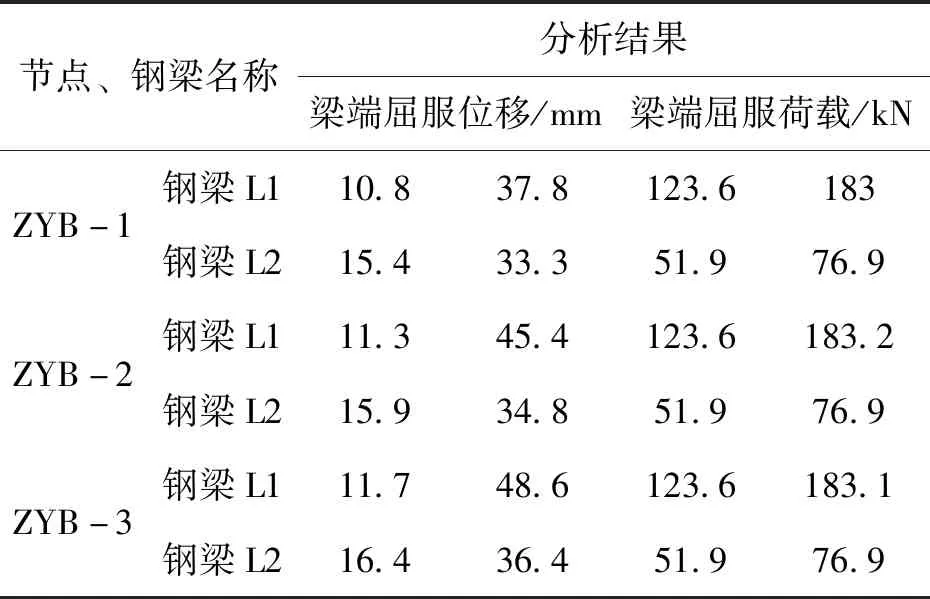
表7 不同轴压比分析结果Tab.7 Analysis results of different axial compression ratios

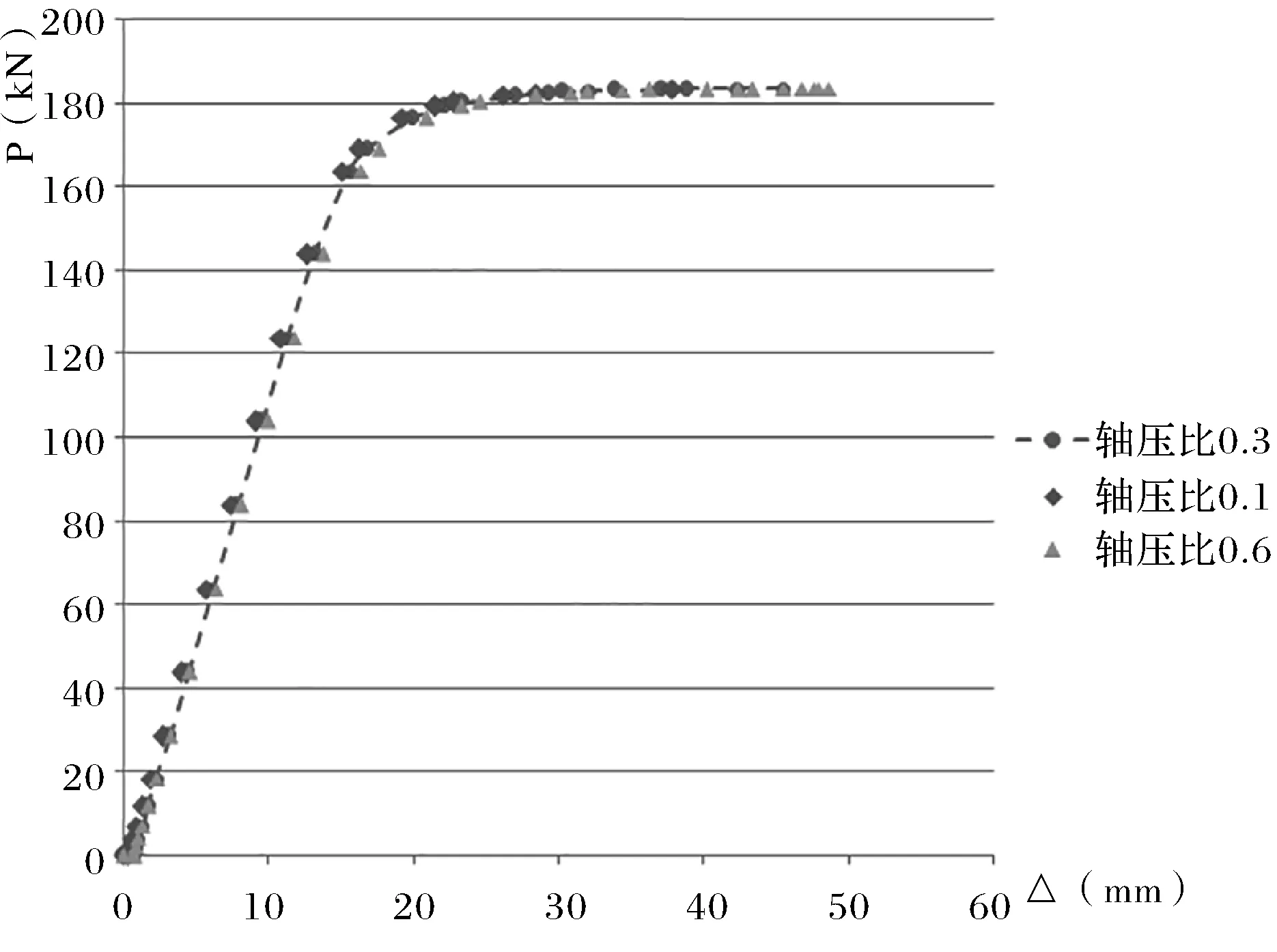
图7 钢梁L1梁端P-Δ曲线对比Fig.7 Comparison of P-Δ curve of steel beam L1 end

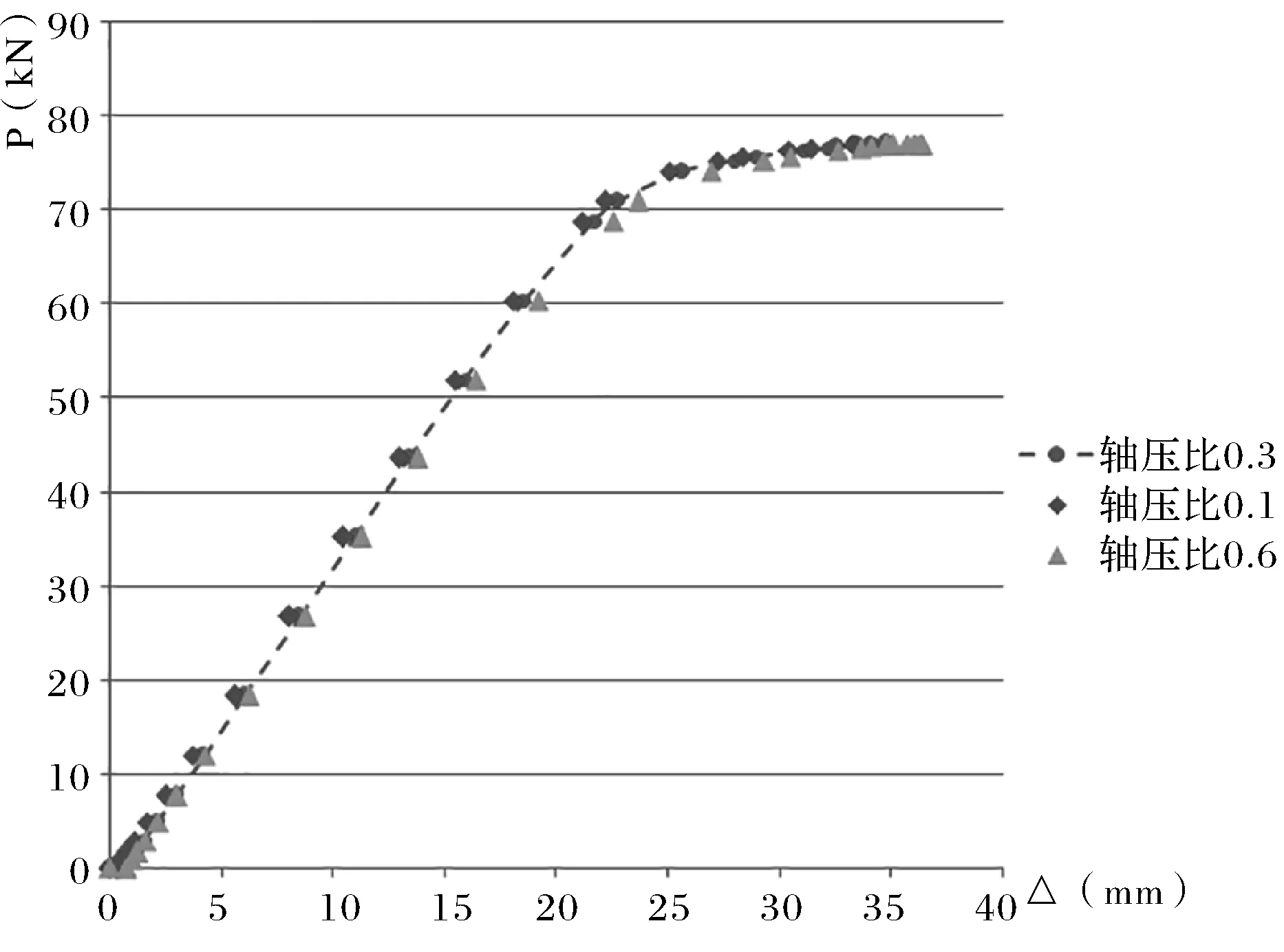
图8 钢梁L2梁端P-Δ曲线对比Fig.8 Comparison of P-Δ curve of steel beam L2 end

2)不同管壁厚对节点力学性能影响分析结果，见表8，梁端P-Δ曲线对比图见图9，图10。

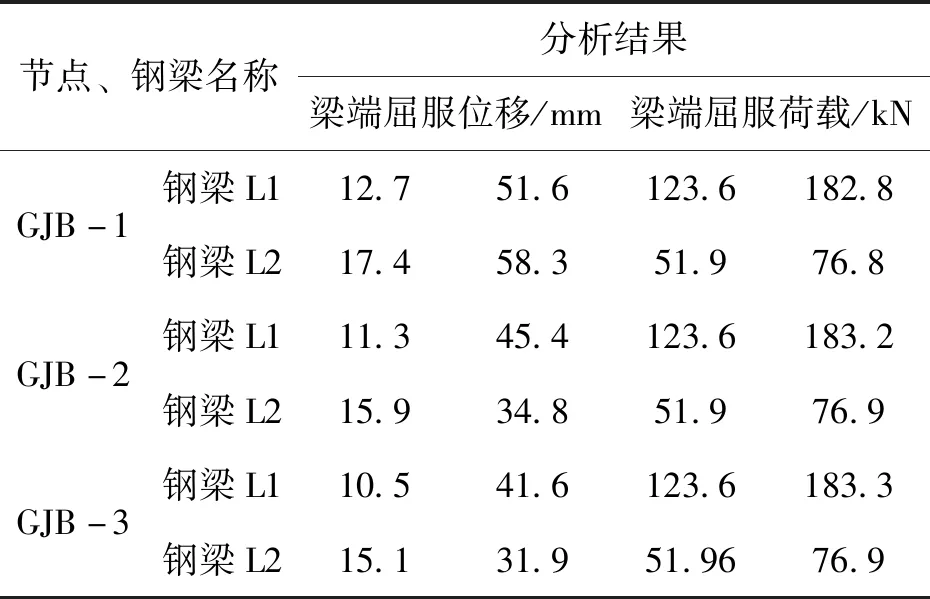
表8 不同管壁厚分析结果Tab.8 Analysis results of different pipe wall thicknesses

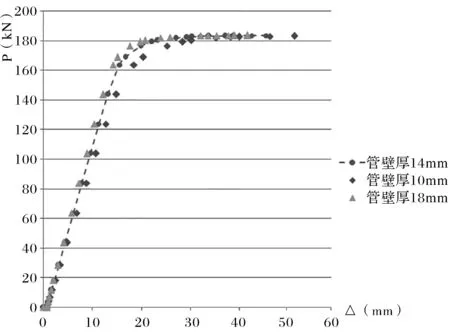
图9 钢梁L1梁端P-Δ曲线对比Fig.9 Comparison of P-Δ curve of steel beam L1 end

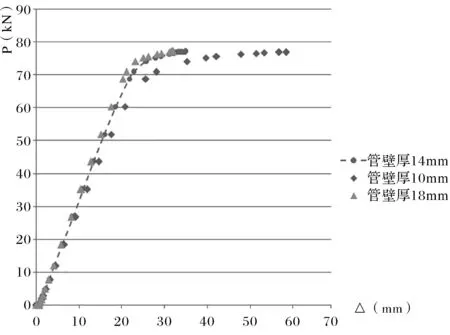
图10 钢梁L2梁端P-Δ曲线对比Fig.10 Comparison of P-Δ curve of steel beam L2 end

c.不同外环板厚度对节点力学性能影响分析结果，见表9，梁端P-Δ曲线对比图见图11，图12。

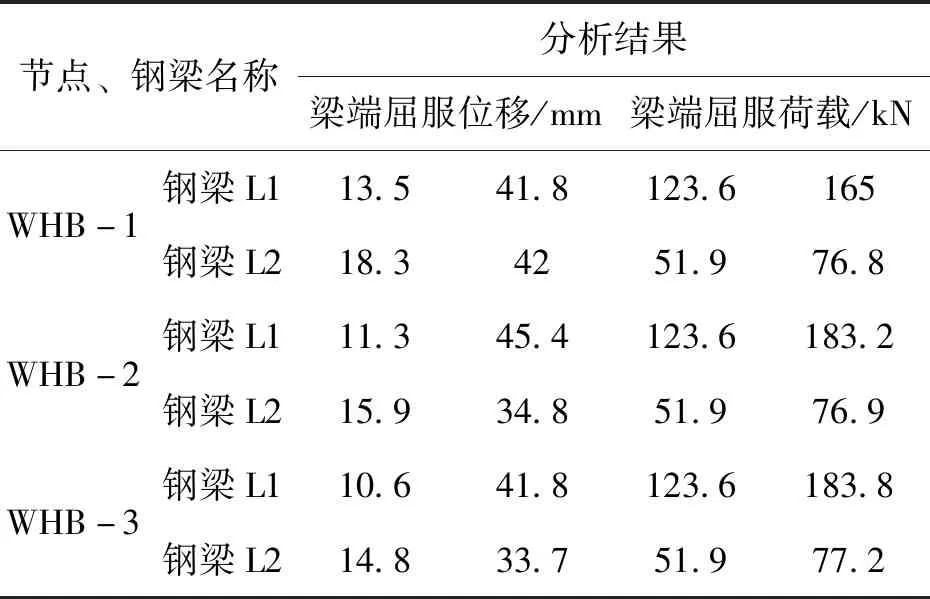
表9 不同外环板厚度分析结果Tab.9 Analysis results of different outer ring plate thicknesses

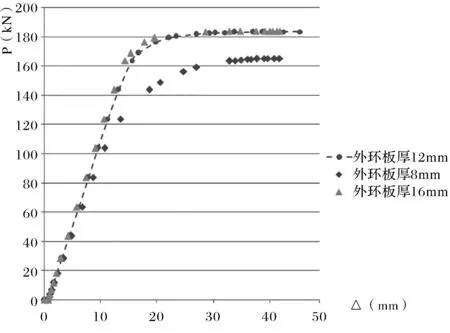
图11 钢梁L1梁端P-Δ曲线对比Fig.11 Comparison of P-Δ curve of steel beam L1 end

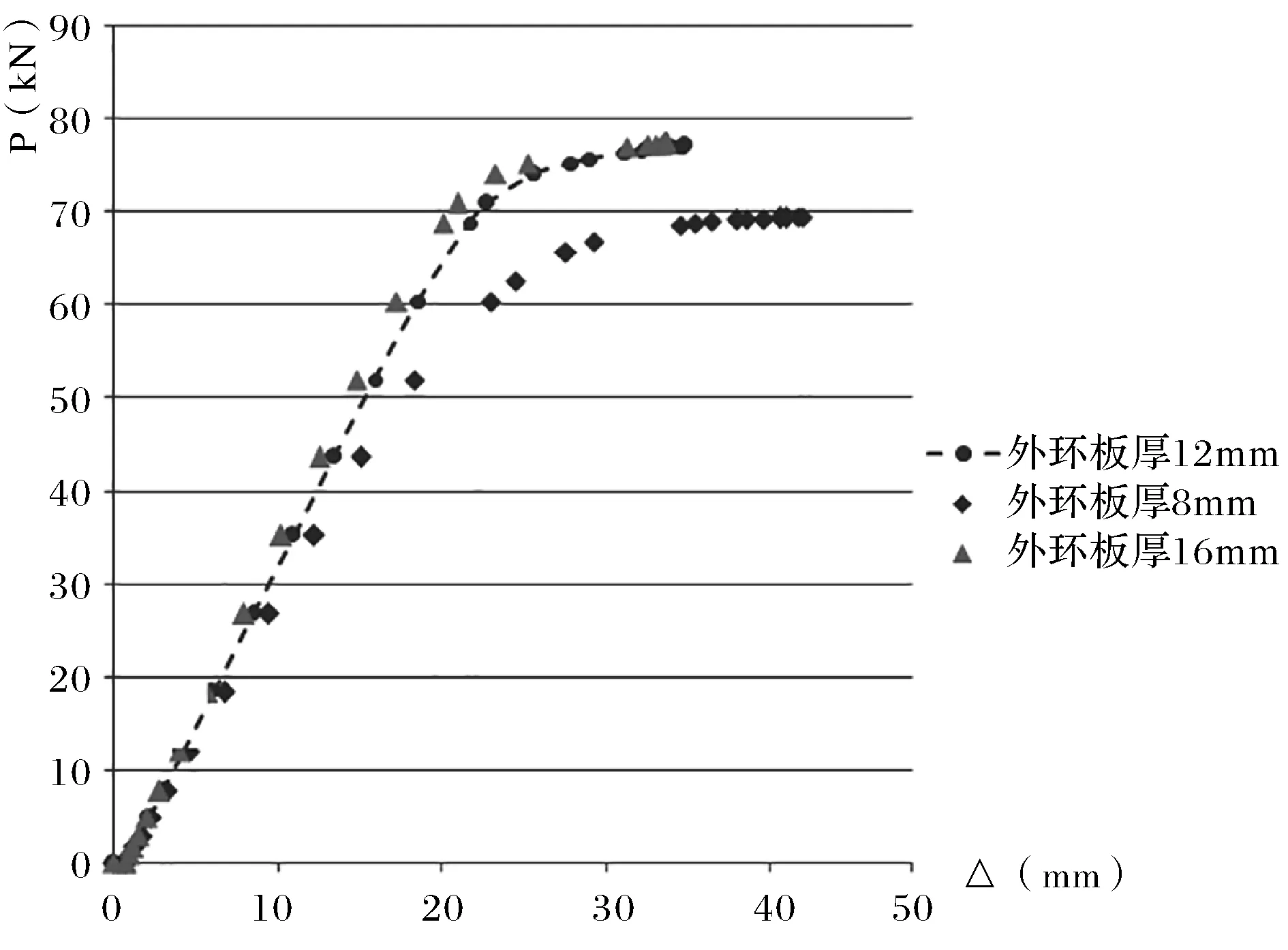
图12 钢梁L2梁端P-Δ曲线对比Fig.12 Comparison of P-Δ curve of steel beam L2 end

6 结 语

1)据图6-11可知，节点两端梁在荷载作用下，节点的P-Δ曲线发展趋势基本一致；

2)据表7-9可知，外环板式节点由于节点刚度和强度均较大，除节点WHB-1外，梁端极限荷载只与钢梁截面大小相关，而梁端屈服荷载，也只与钢梁截面大小相关；

3)据表7-9可知，节点轴压比增加，梁端屈服位移和极限位移均增加，屈服位移增加幅度很小，极限位移增加较明显；随节点管壁厚度增加，屈服位移减小，但极限位移减小量较明显；由于节点WHB-1的外环板厚度小于钢梁翼缘板厚度，其极限位移与节点WHB-3相同，但极限荷载相差很大，屈服位移随外环板厚度增加而减小；节点两端梁高差的增大，使屈服位移增加，但极限位移在减小，发展趋势相反。

4)该文分析各个节点力学性能时，并未加入考虑钢材材料缺陷、节点组装焊接的热效应、焊缝缺陷问题。