重力式码头抛石基床压缩特性和变形参数试验研究
2019-05-18郭林林别社安张炜煌
郭林林,别社安,寇 军,张炜煌
(1.天津大学 水利工程仿真与安全国家重点实验室,天津 300072;2.福建省交通规划设计院,福建 福州 350004)
1 研究背景
抛石基床作为重力式码头、防波堤、沉管隧道等工程中广泛采用的基础型式,其变形特性直接影响其上部结构的安全和稳定。目前的工程中,重力式码头的抛石基床厚度达到40 m,抛石基床的竖向沉降和变形量不可忽略。对于抛石基床的应力和变形研究,数值模拟是常用的研究手段[1-2],数值模拟中材料变形参数的取值决定着计算分析结果的合理性。由于缺乏针对抛石基床的原型试验研究,在数值模型中抛石基床变形参数的选取,一般参照缩尺后的散粒体的室内试验结果[3-8],如柏树田[9]、秦尚林[10]、施维成[11]等研究了不同试验条件下粗粒土的应力-应变关系、强度特性等;褚福永[12]探究了粗粒土卸载-再加载过程的力学特性;刘汉龙[13]、王昊[14]等针对粗粒料特有的颗粒破碎特征进行了深度研究,并讨论了围压、粗粒土含量、含水率、孔隙比等因素对颗粒破碎程度的影响。
现有的散粒体室内试验试样尺度为高60 cm、直径30 cm,试验能模拟粗粒料的最大粒径为60 mm,与工程中抛石基床的10~100 kg块石相差较大,缩尺改变了块石体的级配,影响了颗粒间的填充关系和颗粒的破碎状态,得到的应力-应变曲线必然与实际不同。邵晓泉[15]、张延亿[16]、郦能惠[17]等研究了颗粒尺寸对堆石体压缩变形特性的影响,由于尺寸效应影响因素众多,不同学者的研究成果不尽相同,甚至得出相反的规律[18],因此难以通过修正小尺寸试验结果得到原型尺度材料的变形参数。同时,在荷载作用下,抛石基床的组成颗粒容易发生整体或者局部破碎,导致抛石基床的孔隙比和级配改变,从而影响其力学变形性能,因此抛石基床力学变形性能受应力历史影响较大。重力式码头建筑过程中,抛石基床采用分层随机抛填块石和密实处理的实施方法。抛石基床形成后,再在其上安装上部结构。抛石基床从初始抛填到后期码头使用的过程中,经历了多个受载阶段,才达到从完全松散到密实的过程。因此,工程实际中,抛石基床的变形参数是随受载的应力历史在变化的。
本文通过对重力式码头抛石基床的块石进行原尺度的压缩试验,结合试验现象和测试数据,讨论分析了块石体的颗粒破碎特性、压缩特性和孔隙比的变化特性。本试验采用原尺度块石自然随机抛填形成试样初始状态,再对试样分阶段进行反复加卸载,并利用有限元进行反演分析,得到抛石基床在不同荷载作用次数下、不同密实程度时的应力-应变曲线及变形参数,为重力式码头等工程结构的抛石基床变形研究提供了材料参数。
2 试验研究方法
2.1 试验装置试验设备采用自主研制的大型恒定加载系统,该加载系统主要由底座、料筒、导向柱、压梁、压载板、动滑轮系统、液压顶、加载吊篮等组成,如图1所示。料筒为内径1.5 m、高2 m的上下无顶和底的钢筒,压载板直径1.5 m,荷载由压载板传递到试样表面,保证块石试样顶面全截面受压,试样为轴对称受力状态。该试验装置的加载系统由液压顶、滑轮系统和加载吊篮组成,可保证恒定加载,竖向最大加载压力可达300 t。竖向变形测量采用位移传感器。料筒外侧壁距底端1/3和2/3处贴有横、纵8对应变片,测量料筒不同部位的环向变形量,取各测点的平均值作为料筒的环向变形量。装填块石时,在料筒内壁涂抹黄油,以减小块石试样与料筒之间的竖向摩擦力,同时避免块石的尖角接触料筒粘贴应变片的部位。

图1 试验装置

图2 块石试样
2.2 试样制备与试验方案试验块石为重力式码头抛石基床填筑所用的10~80 kg工程块石,石料主体为灰岩类,包括灰岩、白云质灰岩,抗压强度为50~100 MPa。块石最大粒径为300 mm,试样直径为1.5 m,试样高度为2 m,试样直径与最大粒径之比不小于5,试样高度与最大粒径之比不小于6.7,满足土工试验制样要求,块石试样如图2所示。
重力式码头建筑过程中,先随机抛填形成抛石基床,接着对其进行密实处理,然后在其上安装上部结构,抛石基床经历从完全松散到密实的过程。在码头施工期间,抛石基床经历了加载、卸载再加载,在码头使用时期抛石基床的应力可能大于历史最大应力,出现超加载的情况。为研究抛石基床从松散到密实各个阶段的压缩特性,本试验试样在保证级配曲线均匀连续的情况下,自然抛填而成。由于本试验试样颗粒粒径大、重量大,难以通过筛分法确定粒径级配曲线,并且10~80 kg之间块石颗粒粒径数量级跨度小,常规的粒径级配曲线难以反映试样的颗粒组成。然而,本试验块石各向尺寸差异较小,粒径统计与重量统计结果存在一一对应关系,在港口工程中,习惯采用重量描述块石的尺度,故用颗粒重量代替颗粒粒径绘制级配曲线,5组试样的重量级配曲线如图3所示。为考虑试样初始状态和加载次数对块石压缩特性和变形参数的影响,进行了多组重复加卸载试验,试验方案如表1所示。试验采用分级加载,初始荷载应力为200 kPa,后续每级加载的荷载应力增量为100 kPa。加载的最大应力值为1600 kPa,大于一般工程中抛石基床的最大应力1000 kPa左右。
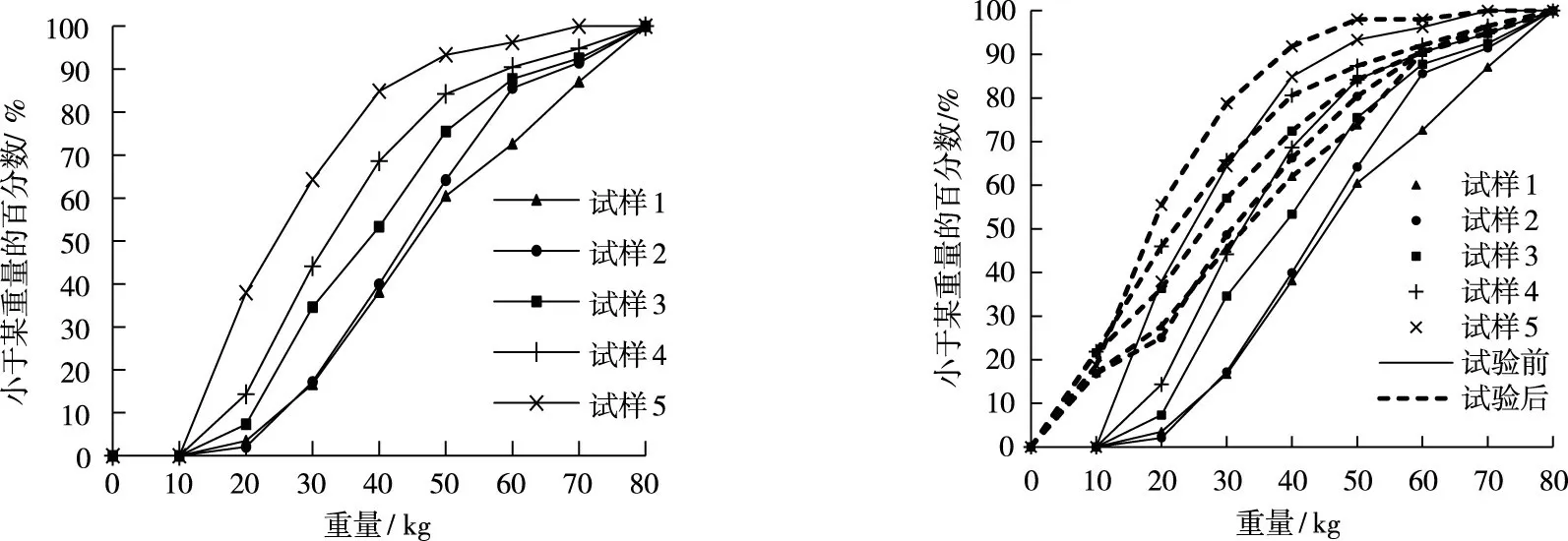
图3 试样重量级配曲线

表1 试验方案
3 试验结果分析
3.1 颗粒破碎特性试样在加载过程中颗粒破碎现象明显。图4为试验前后,试样颗粒的重量级配累积曲线。可以看到,试验后的曲线均向左侧移动,试验前重量小于10 kg 的颗粒含量为零,试验后其含量大幅增加,说明荷载作用下块石颗粒发生破碎,导致试样级配改变,大颗粒含量减小、小颗粒含量增加。
常用的三种度量颗粒破碎程度的指标为:(1)Marsal[19]提出的试验前后颗粒级配曲线上各粒组含量差值之和的颗粒破碎率Bg;(2)柏树田[9]建议的试验前后限制粒径G60之差B60;(3)Hardin[20]提出的由破碎量和破碎势比值得到的相对颗粒破碎率Br。与粒径级配曲线一致,可从试样重量累积曲线中求得对应的颗粒破碎指标,表2列出了加载完成后5组试样的三种度量指标以及初始控制重量G60。可以看出,B60和Br值的变化趋势相同,而Bg与之相比有较大差异,进一步分析可知,由于试样颗粒粒组范围大、破碎程度高,Marsal 的颗粒破碎率Bg只计算了某几个粒组含量的变化,不能反映试验前、后各粒组的整体变化情况。从表2中各组试样的B60和Br值可以看出,与加载次数和初始孔隙比相比,粒径的大小对颗粒破碎程度的影响更为明显,控制颗粒重量G60越大颗粒破碎越剧烈,这与文献[9]和文献[14]的结论一致。

图4 试验前后试样重量级配曲线

表2 颗粒破碎程度指标
3.2 压缩特性在试验所加的荷载条件下,块石体的压缩曲线整体呈线性分布。图5(a)为一次加载过程中试样的荷载-压缩量关系曲线,可以看出曲线存在细微的波动,主要原因是:在荷载作用下,块石颗粒发生破碎,且由于块石颗粒内部结构的不确定性、外部接触方式的多样性导致块石颗粒破碎具有较强的随机性,使得在荷载作用下压缩量的增量不均匀。图5(b)为多次加载过程中试样的荷载-压缩量关系曲线,可以看出块石体初次加荷时,颗粒产生移动、破碎,压缩量增加,卸荷时回弹量很小,再次加荷时,当荷载未超过之前的最大荷载时,颗粒的移动、破碎不明显,故块石体的变形较小,当荷载超过之前的最大荷载时,颗粒的移动、破碎继续产生,块石体变形增大。多次加卸荷循环后,颗粒破碎和颗粒移动逐渐减少,堆石体变形量降低,压缩模量增大。
从图5(b)中可以看到,多次加卸荷循环后,随着试样压实度的提高试样的压缩模量显著增大。块石的压实状态实质上是块石颗粒间的接触状态,根据块石体的压缩特性,块石体卸载后的回弹量极其微小,即卸载对块石颗粒间的接触状态基本无影响,则块石的压实状态由应力历史决定。因此可以通过历史最大应力和最大应力作用次数这两个描述应力历史的指标,来反映块石体的压实状态。
3.3 孔隙比变化特性抛石基床这类散粒体材料压缩变形产生的机理与黏土有本质的区别。一般认为黏土压缩的根本原因在于土体中的孔隙逐渐消失,土颗粒是不能被压缩的,故黏土的压缩表现为弹塑性,并且具有时间效应。李建民[21]在研究土体再压缩变形规律时,对黏土进行了卸荷回弹再压缩试验,得到其e-p曲线如图6(a)所示,可以看出黏土受到一定压力后卸载回弹明显,再次加载的压缩曲线的非线性特性明显,与初次加载曲线在形状和趋势上并无显著的区别。
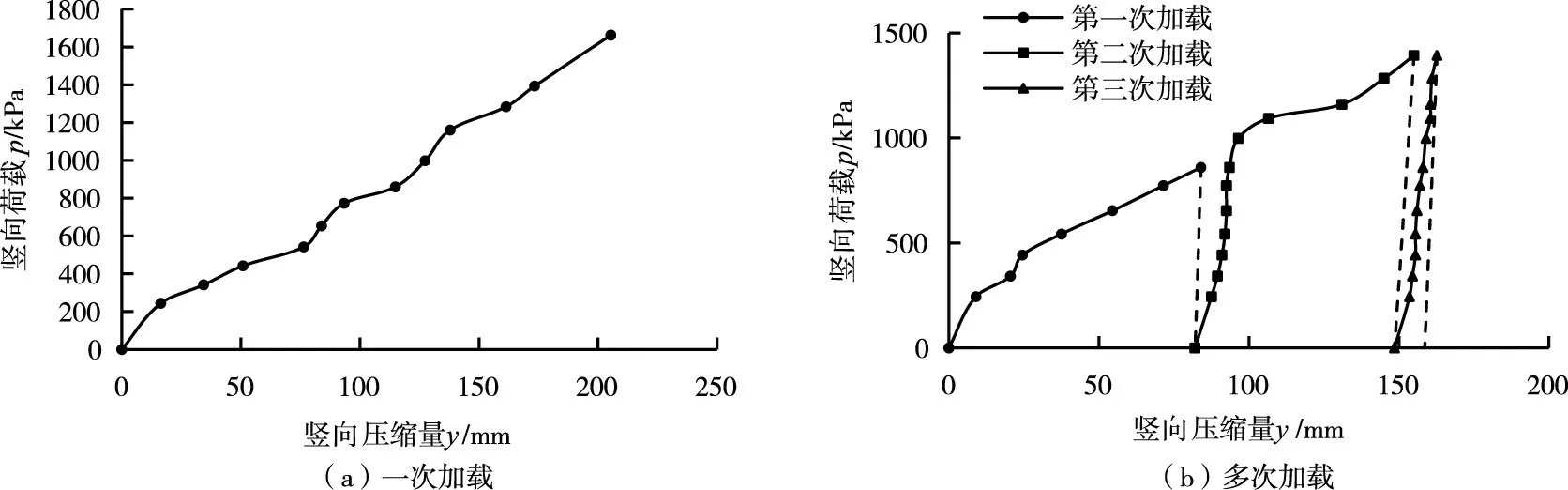
图5 试样荷载-压缩量曲线
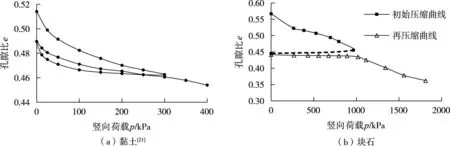
图6 再加载e-p曲线
而对于块石体这类散粒体材料,外荷载的作用主要由块石颗粒构成的骨架承担。在加载过程中颗粒发生滑动、滚动以及破碎,骨架结构发生变化,宏观体现为块石体的抗压能力提高,以及块石体的孔隙比减小、压缩模量增大。卸载过程对块石体的骨架基本无影响,卸载后的块石体骨架对先期应力具有记忆性,当再次加载的荷载超过先期应力后块石体骨架开始重新大幅度的变化。图6(b)为本试验得到的块石体的压缩曲线,可以看出块石受到压力后卸载无明显回弹,并且再次加载的压缩曲线有明显的拐点,拐点对应的荷载值为初次加载时的最大荷载。对于再次加载阶段,当荷载小于初次最大荷载值时,孔隙比随荷载线性变化且变化量很小,当荷载超过初次最大荷载值后,孔隙比随荷载的变化量增大,此时e-p曲线与初次加载曲线趋势一致。
4 变形参数分析
4.1 参数计算变形模量是计算抛石基床压缩变形量的重要参数。本文试验模型在竖向荷载作用下的压缩过程中,单个块石颗粒的受力和应力状态较为复杂,理论和数值分析时,采用块石体的平均受力状态来表征实际的随机状态,将块石体的侧限压缩简化为空间轴对称问题来考虑。假设块石体为各向均质材料,在不考虑体力的情况下,当圆柱体外侧压力为σρR,顶部压力为σz0时,有:

式中σρ、σφ、σz分别为块石体的径向应力、环向应力和竖向应力。
根据空间轴对称问题的物理方程,块石体竖向应变为:

根据应变的物理含义,有:

联立式(1)—(4)则有:

试验过程中,试样外侧被钢制料筒限制,试样外侧压力σρR等于料筒内壁所受应力,则料筒外侧壁径向应力为零,环向应力可由下列式子计算:

则块石体的环向应力为:

将式(8)代入式(5)中,可得:

式中:E为块石体的变形模量,kN/m2;μ为块石体的泊松比;Es为钢材的弹性模量,kN/m2;εs为料筒的环向应变,图7为料筒外侧壁距底端1/3和2/3处,共8个测点的筒壁环向应变随荷载的变化关系曲线,筒壁环向应变量随着荷载增加逐渐增大,取各测点的平均值作为料筒的环向变形量;σz0为块石体顶面压力,kPa,即为施加在块石表面的荷载;y 为块石体的竖向压缩量,mm,可通过试验测得;h为试样高度,mm;D 为料筒的直径,m;δ为料筒的壁厚,m。根据加载试验的测试数据,可拟合计算E和μ。
4.2 数值模拟建立试验的有限元模型,给一个块石体的初始泊松比,代入式(9)计算其变形模量,输入到数值模型中计算分析试样的压缩量,反复迭代至数值模型分析结果与试验测试结果吻合,从而得到块石体的变形模量和泊松比值,有限元反演计算流程如图8 所示。数值模型中包括料筒、块石和压载板,各个部分的尺寸均与物理试验中一致。料筒和压载板为Q235 型钢材制作,采用Q235 型钢的杨氏弹性模量和泊松比,即Es=2.06×105MPa,μ=0.304。采用Mohr-Coulomb 准则来描述块石体的屈服和破坏行为,块石内摩擦角为45°,黏聚力为0 kPa。
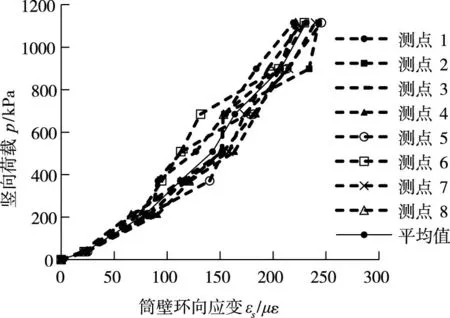
图7 荷载-料筒的环向应变关系曲线
4.3 计算结果分析由于每次加载过程中试样的初始高度不同,则需分别建立5组试样各次加载过程的数值模型,依据全量法利用有限元反演每级荷载下块石体的泊松比和变形模量(割线变形模量)。图9为试样1 第14 级加载时,当泊松比分别取0.2、0.3、0.4 时,由式(9)计算得到的块石变形模量代入有限元模型中,得到的块石顶面的荷载-压缩量曲线,具体计算结果列入表3 中,由图中曲线可以看到试验测得的荷载-压缩量曲线介于泊松比取0.2和0.3的计算结果之间,从表中数据可知在该区间内当泊松比取不同值时,有限元反演得到的块石试样的压缩量差异较小,且均与实测压缩量偏差率小于10%,同时泊松比的变化对块石体变形模量的影响也较小,综上抛石基床泊松比取值介于0.2~0.3之间均可满足计算精度要求。
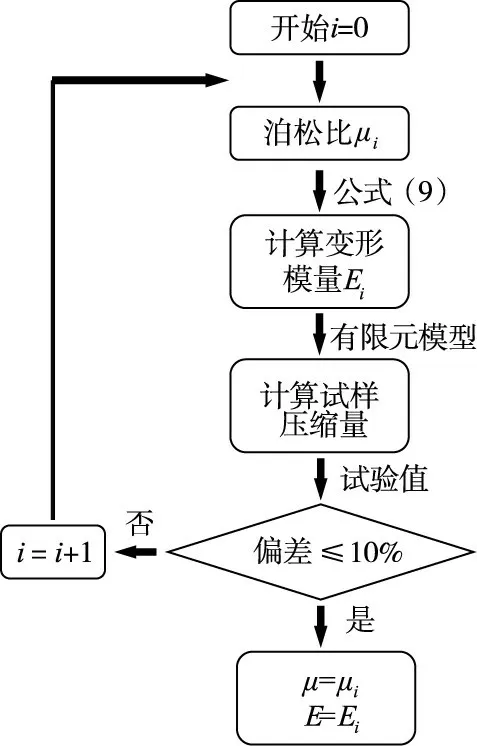
图8 有限元反演流程图
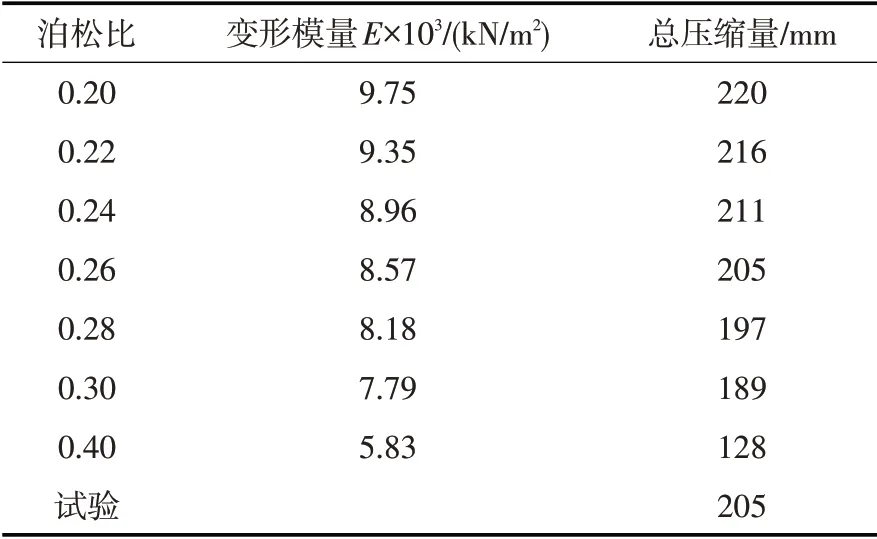
表3 不同泊松比有限元反演结果
根据有限元反演出的5组试样各次加载过程中各级荷载下的割线变形模量,绘制出试样的轴向应力-应变关系曲线,如图10所示。由图中曲线可以得出如下结论:(1)块石体第一次加载过程中,其应力-应变曲线近似线性分布,并且卸载后块石体的回弹量极小;(2)块石体经过加卸载后,再次加载时,其应力-应变曲线在历史最大应力处有明显的拐点,拐点前后曲线均近似线性分布;(3)随着荷载作用次数的增加,块石体应力-应变曲线斜率逐渐增大,当荷载作用次数超过三次后,应力-应变曲线斜率基本不再增加。因此可将抛石基床变形模量按荷载作用次数分为初次压缩变形模量E1、再次压缩变形模量E2和多次压缩变形模量Em三种,来反映不同压实状态下抛石基床的压缩特性。
4.4 变形模量拟合结果初次压缩变形模量E1表示抛石基床第一次受到某一荷载作用时其应力-应变关系曲线的斜率,再次压缩变形模量E2表示抛石基床第二次受到某一荷载作用时其应力-应变关系曲线的斜率,多次压缩变形模量Em表示抛石基床第三次或者三次以上受到某一荷载作用时其应力-应变关系曲线的斜率。综合整理得到5组试样各次压缩时的应力-应变关系,如图11所示,采用线性方程σ=Eε对各曲线进行拟合,表4列出了各组试样各次压缩时的应力-应变关系拟合系数,拟合可决系数R2值普遍大于0.90,拟合效果良好。
结合表1和2分析可知,块石体初次压缩变形模量E1的大小受颗粒破碎程度和初始孔隙比共同影响,块石体孔隙增加,抗压能力减弱;颗粒破碎程度减弱,由块石颗粒破碎导致的压缩变形减小。从试验结果来看,块石体孔隙比的变化对初次压缩变形模量E1的大小影响不明显,块石体颗粒破碎程度越大(表2中B60和Br值越大),初次压缩变形模量E1越小,但是总体来看5组试样初次压缩变形模量较为接近。
对于三种变形模量中的每一种,各组试样的结果较为接近,可取各组试样结果的平均值作为抛石基床相应变形模量的参考值,初次压缩变形模量、再次压缩变形模量和多次压缩变形模量分别为11.5×103、150×103和184×103kN/m2。
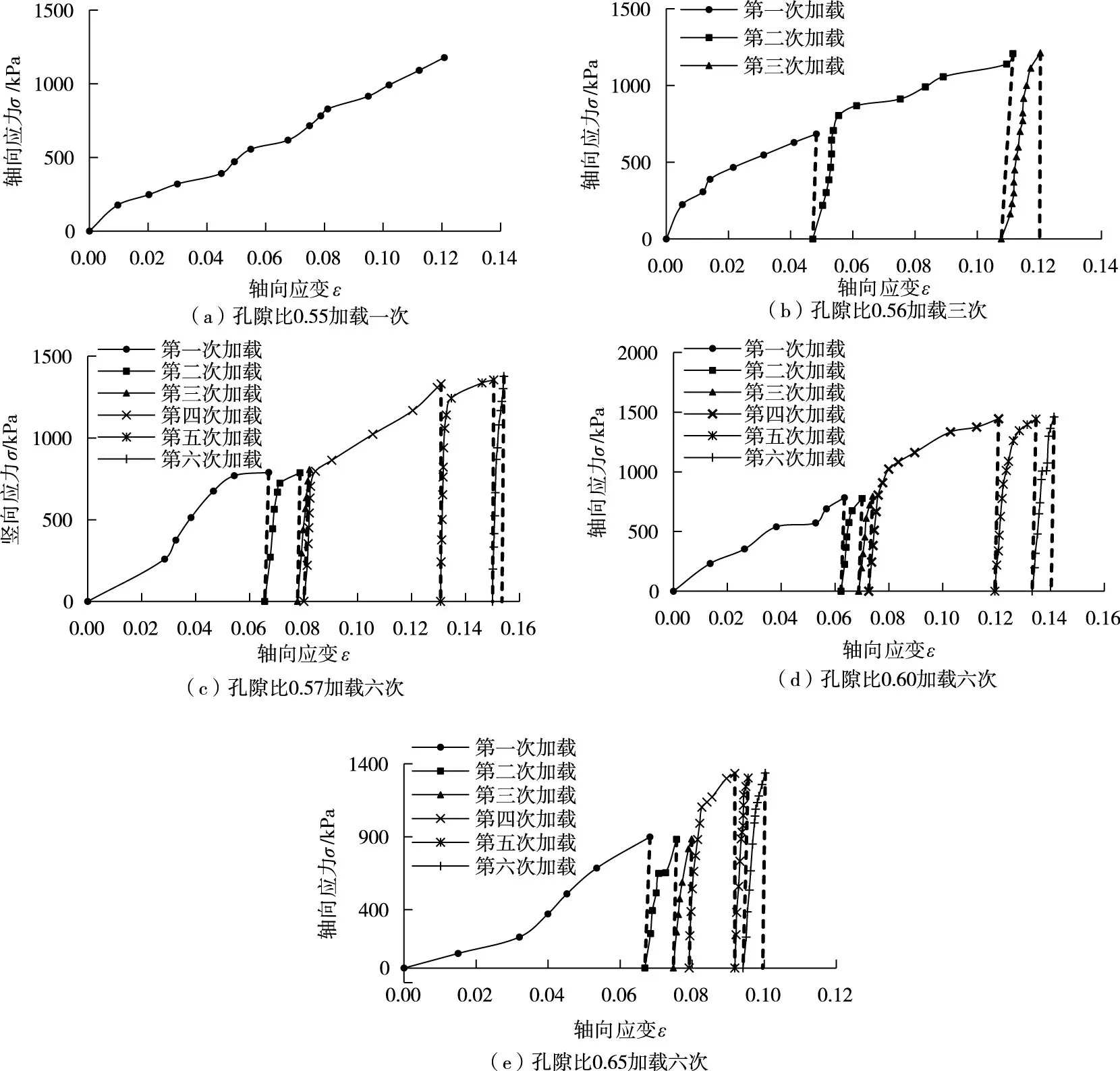
图10 试样应力-应变曲线
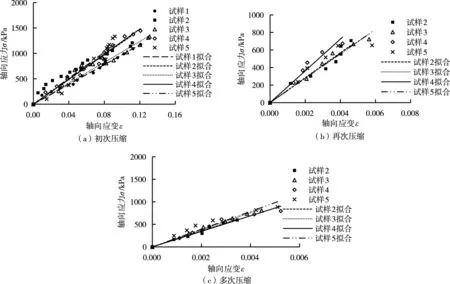
图11 试样的应力-应变关系拟合曲线
4.5 应力-应变曲线分段线性表示通过对块石体应力-应变曲线分析可以看出,曲线在历史最大应力处有明显的拐点,拐点前后曲线均近似线性分布,直线的斜率因荷载作用次数的不同而不同。因此可将抛石基床的应力-应变曲线进行分段线性表示,即以荷载作用次数为依据,寻找不同作用次数下的历史最大应力,将各个历史最大应力作为应力-应变曲线的分段点,各分段点间通过直线连接,直线斜率取对应的变形模量。同时,抛石基床压缩变形中弹性变形与塑性变形相比可忽略不计,即卸载时抛石基床无回弹。
图12为分段线性表示的一个反复加卸载过程的抛石基床的应力-应变曲线。抛石基床加载至A点应力水平后卸载,再进行重加载至D 点应力水平,卸载后又加载至H 点应力水平。对于BCD 加载段,以荷载作用次数为依据,可找到一个分段点即C点,C点前的加载过程在历史中有过一次加载即OA段,故该段直线斜率为再次压缩变形模量E2,C点后的加载过程在历史中没有加载,故该段直线斜率为初次压缩变形模量E1;同理对于EFGH加载段,可找到两个分段点即F点和G点,F点前的加载过程在历史中有过两次加载即OA、BC段,故该段直线斜率为多次压缩变形模量Em,F点到G点间的加载过程在历史中有过一次加载即CD段,故该段直线斜率为再次压缩变形模量E2,G点后的加载过程在历史中没有加载,故该段直线斜率为初次压缩变形模量E1。
图13为基于三种变形模量的抛石基床应力-应变曲线分段线性拟合方法在工程问题中的应用,图13(a)为施工阶段抛石基床的应力值变化示意图,总共包括5次加载过程,其中OA、BC、DE和FG为4次爆夯的加载过程,HIJKLM为沉箱安放至面层施工阶段的加载过程(HI为沉箱安放,IJ为沉箱内、后回填,JK为胸墙一层浇筑,KL为胸墙二层浇筑,LM为面层施工)。在第5次加载时,根据应力历史,可将荷载分为三段,Ⅲ为多次加载段,该区域荷载历史作用次数为2次或者2次以上;Ⅱ为再次加载段,该区域荷载历史作用次数为1次;Ⅰ为初次加载段,该区域荷载抛石基床未曾加载过。将抛石基床的应力值依据作用次数进行分段,选择对应的压缩变形模量,可绘制应力-应变关系曲线如图13(b)所示,则抛石基床在施工过程中各个阶段的应变值均可从曲线中查得。
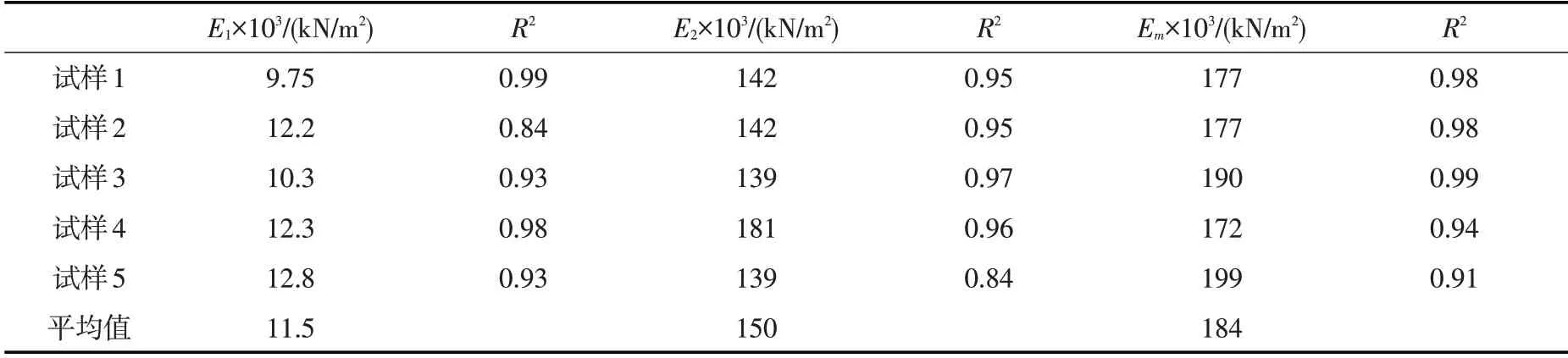
表4 试样应力-应变关系拟合系数
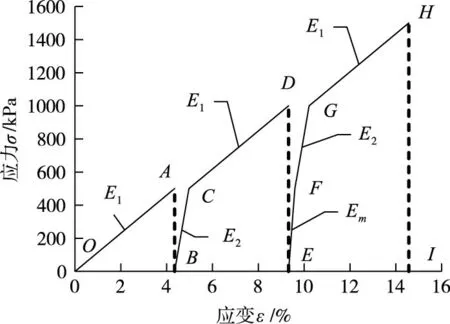
图12 抛石基床应力应变曲线分段线性拟合示意图
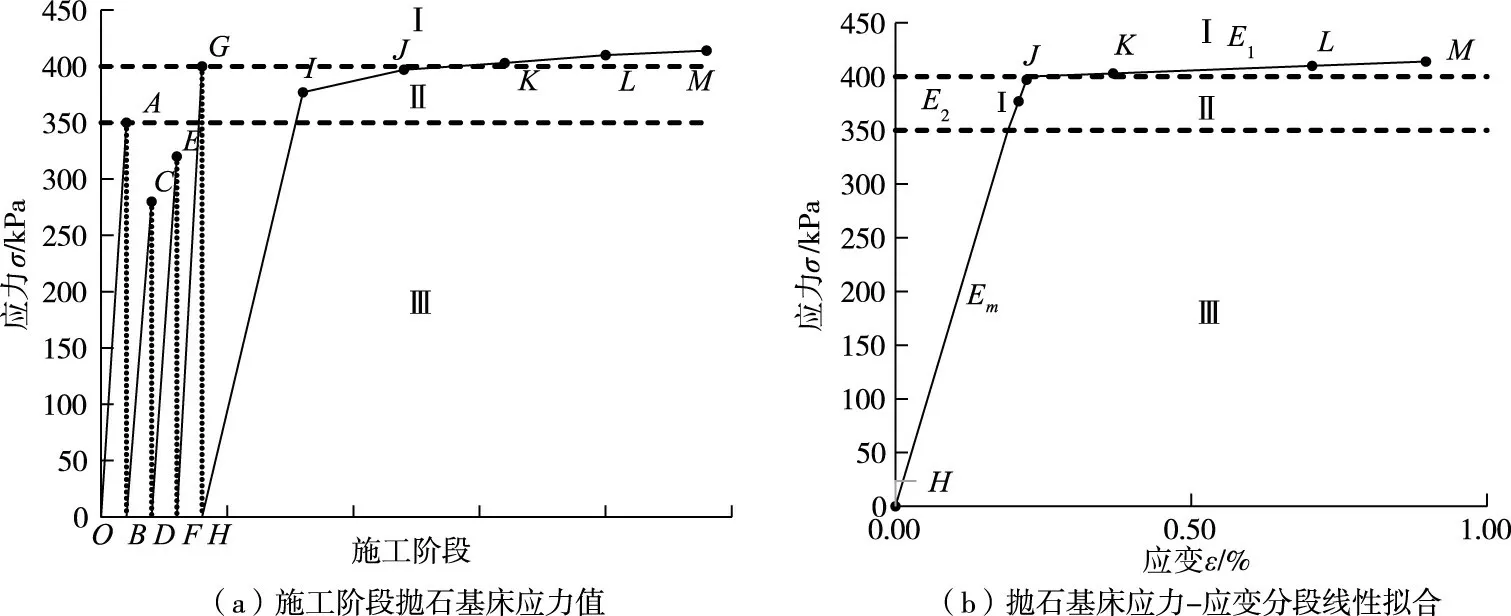
图13 变形模量在重力式码头工程中的应用
5 结论
通过对重力式码头抛石基床填筑所用的10 ~80 kg块石体进行原尺度压缩试验研究,分析抛石基床的压缩特性和变形模量,得到结论如下:
(1)抛石基床在加载过程中颗粒破碎现象明显,与加载次数和初始孔隙比相比,粒径的大小对颗粒破碎程度的影响更为明显,粒径越大颗粒破碎越剧烈。
(2)抛石基床的压缩变形以塑性变形为主。抛石基床的应力历史决定了抛石基床的压实程度,影响着抛石基床的压缩特性以及压缩模量的大小,可通过历史最大应力和荷载作用次数这两个参数作为描述应力历史的指标,来反映块石体的压实状态。
(3)抛石基床的e-p曲线与黏土有显著区别,具体表现为抛石基床受到一定压力后卸载,再次加载时的压缩曲线有明显的拐点,拐点位于历史最大应力处,当应力小于历史最大应力时随着应力的增加孔隙比变化量很小,当应力超过历史最大应力后,孔隙比随应力的变化量增大,此时e-p曲线与初次加载曲线趋势一致。
(4)依据应力程度和作用次数,重力式码头抛石基床变形模量可分为3 种:初次压缩变形模量E1、再次压缩变形模量E2和多次压缩变形模量Em;抛石基床的应力-应变曲线可分段线性表示,不同荷载作用次数的历史最大应力为曲线分段点,各分段点间通过直线连接,直线斜率取对应作用次数下的变形模量。该分段线性拟合方法中3种变形模量的值较为关键,本文通过5组试验得出3个变形模量的参考值,但试验组数尚少,需进一步完善研究。
