婚姻稳定性与生育率变动关系的理论与实证分析

□ 莫玮俏

内容提要 本文对婚姻稳定性与生育率的影响关系进行了理论与实证研究。 在理论方面，构建生育模型，将婚姻稳定性分为与生育率相关的内生部分和不相关的外生部分，分析得到，当外生因素不变时，婚姻稳定性和生育率处于均衡水平；当不利于婚姻稳定性的外生因素增强时，生育率降低。 同时，利用CGSS 微观调查数据检验婚姻稳定性对生育率的影响效应，通过区分非流动和流动人口的影响差异来识别内生和外生效应。实证结果表明，婚姻稳定性对生育率具有总体正向效应，其中，农村非流动人口的婚姻稳定性对生育率没有显著影响，而流动人口的婚姻稳定性对生育率具有显著正向影响。 由于人口流动对婚姻稳定性具有负的外部冲击，进而对生育率产生局部均衡影响，使得生育率降低。

一、引言

20 世纪六七十年代以来，西方社会的婚姻家庭发生了重大变化，社会生育率明显下降，离婚率明显上升， 这使得关注婚姻稳定性和生育率的文献不断涌现。近几十年来，有关婚姻稳定性和生育率方面的研究已经在理论和实证方面取得了重要成果， 多数研究表明婚姻稳定性与生育率之间存在相互影响的关系。长期以来，我国执行了严格的计划生育政策，社会生育率明显下降。党的十八届五中全会后， 我国继单独二孩政策以后全面实施了一对夫妇可生育两个孩子政策。 但“全面二孩”政策的实施， 并未完全改变全国二孩生育数量低于预期的困局， 生育率低下在很大程度上已成为一种趋势， 持续的低生育和少子化正在成为人口发展的新常态。然而，与生育率下降形成鲜明对比的是，社会离婚率不断上升。从已有的理论和经验来看，这“一降一升”背后的逻辑值得关注和思考。本文在考虑生育率对婚姻稳定性具有反馈效应的基础上， 着重分析婚姻稳定性对生育率的影响机制和效果。在理论方面，将婚姻稳定性分为受生育率影响的内生部分和不受生育率影响的外生部分，通过构建生育模型，分析婚姻稳定性影响生育率的内生效应和外生效应。 在实证方面， 采用CGSS 微观调查数据来进行检验，从婚姻状况和受访者对待性行为的态度两个角度衡量婚姻稳定性， 既考察了婚姻稳定性对生育率的总体影响效应， 也通过区分流动人口和非流动人口的影响差异来识别婚姻稳定性影响生育率的内生和外生两种效应。

二、文献回顾与评述

到目前为止， 有关婚姻稳定性与生育率的相关性研究主要集中在生育率对婚姻稳定性的影响、 婚姻稳定性对生育率的影响以及两者之间的相互影响三个方面。 生育率对婚姻稳定性的影响机制在于，子女作为婚姻的特殊资产，通过增加当前婚姻的吸引力和提高离婚成本， 来增加婚姻稳定性（Becker，1973；Becker et al.，1977）；或者子女作为婚姻中不可传递的人力资本， 会对再婚产生不利影响， 因此有利于现有婚姻的稳定（Andersson，1997；Chiswick，1990）。 一些实证研究表明，生育孩子确实使得夫妻的离婚风险降低， 生育数量越多，离婚概率越低（Waite&Lillard，1991；许琪等，2013）。 但 是Christensen&Philbrick （1952）、Udry（1981）等指出生育率与婚姻稳定性之间的关系还必须考虑理想的家庭规模， 只有当生育数量与家庭成员的理想生育数量匹配时， 婚姻关系的满意度达到最高， 而生育率太高或太低都会使得婚姻稳定性下降。 由于早期对生育数量影响婚姻稳定性的实证分析大多采用OLS 回归的方法，这种方法并不能真正识别因果效应。为此，一些研究采用工具变量（IVs）法去识别家庭规模对婚姻的影响（Bronars&Grogger，1994；Jacobsen et al.，2001；Bellido et al.，2013；Silles，2014）。 Jacobsen et al.（2001）利用第一胎生育双胞胎的数据进行回归得到， 在短期由于第一胎生育双胞胎导致的生育率上升对离婚率没有影响，但从长期来看，却会导致离婚率升高。 Silles（2014）也发现在计划内增加的生育数量有助于降低离婚率， 而在非计划内增加的生育数量则使得离婚升高。 这些研究表明生育率对婚姻稳定性的影响并非是线性的， 并且与家庭理想规模有关。

婚姻稳定性对生育率影响的作用机制表明，婚姻关系不稳定的夫妻交流频率减少使得生育孩子 的 可 能 性 降 低（Cohen&Sweet，1974；Thornton，1977、1978）； 或者因为考虑到孩子使得离婚成本升高， 因而婚姻越不稳定的夫妻生育率越低（Lillard&Waite，1991，1993）； 或者由于单亲家庭不利于孩子的成长， 导致生育率下降（Amato&Keith，1991 等）。 而在研究婚姻稳定性和生育率之间相互影响的关系时，Waite&Lillard（1991）认为两者之间存在多重反馈机制。婚姻稳定性下降，一方面导致生育率降低， 另一方面由于家庭成员预期到孩子能够降低离婚风险，巩固婚姻关系，因而容易导致早孕，使得生育率回升（Friedman et al.，1994）。婚姻稳定性增强为增加孩子提供有利环境， 而婚姻稳定性降低也可以通过生育孩子来进行修复和改善（Rijken&Liefbroer，2009）。因此婚姻稳定性与生育率之间存在非线性关系， 即当婚姻处于某种稳定程度时， 生育数量达到最大（Rijken&Thomson，2011）。

相比国外， 国内鲜有研究关注婚姻稳定性与生育率的关系。 许琪等（2013）考察了生育对婚姻关系的影响，发现婚前生育不利于婚姻的稳定，生育子女数量多对婚姻稳定有利但边际效应递减。然而该研究没有考虑婚姻稳定性对生育的反向作用， 因而无法准确得到生育率与婚姻稳定性的关系。另一方面，目前还没有文献具体讨论过婚姻稳定性对生育率的影响。本文基于现有研究的不足，在考虑生育率对婚姻稳定性影响的基础上， 从理论和实证两个方面分析婚姻稳定性对生育率的作用机制和影响效应。

三、理论分析

1.模型的假设条件

本文构建的生育模型包含以下几个基本假设：

（1）集体决策模型，即家庭成员的效用函数是可分离的，家庭决策取决于夫妻双方的议价能力。

（2）代表性家庭共有两期经历，第一期处于结婚状态并决定生育数量， 第二期维持婚姻的概率为p（0≤p≤1），离婚风险为（1-p）；

（3）婚姻稳定性p 既包含受生育数量影响的内生部分，也包含不受生育数量影响的外生部分；

（4） 生育率还取决于家庭成员的理想生育数量，因此是非线性函数；

（5） 第二期离婚家庭抚养孩子的单位时间成本高于在婚家庭；

（6）男性和女性都具有1 单位时间，采用时间二分法， 女性的1 单位时间在抚育孩子和市场劳动上进行分配， 男性将1 单位时间全部用于市场劳动。

设定第二期在婚家庭（p=1）女性的议价能力为θ1，则男性的议价能力（1-θ1）。 女性抚育一个孩子的时间为τ， 抚育Q 个孩子的总时间为τQ；女性的市场工资率为wf，则市场收入为wf（1-τQ）。男性市场工资率为wm，则市场收入为wm。 qi表示在婚家庭成员的理想生育数量， 生育数量的效用函数形式设为消费效用函数形式设为在婚家庭具有固定的婚姻收益φ①。

设定第二期离婚家庭（p=0）女性的理想生育数量为q0/j0，消费数量为c0/j0；男性的理想生育数量为q0/m0，消费数量为c0/m0；婚姻的固定效用φ消失。由于离婚后男性一般要支付女性赡养费用，假定双方通过谈判， 采取合作的方式实现生育孩子数量和消费分配的帕雷托最优结果， 女性的谈判能力为θ2，男性的谈判能力为（1-θ2）。 离婚后由女性抚育孩子，抚养的单位时间成本为τ'，τ'〉τ。

由于本文假定婚姻稳定性p 由受生育数量影响的内生部分和不受生育数量影响的外生部分组成， 且生育数量与家庭成员的理想生育数量匹配时， 婚姻关系的满意度达到最高（Christensen&Philbrick，1952；Udry，1981；Jacobsen et al.，2001；Silles，2014）。 设定p 关于Q 的反映函数如下：

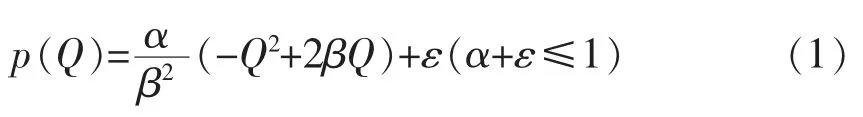
由公式（1）可得：

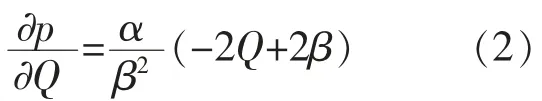
2.基本模型

家庭中夫妻双方的目标是最大化两期效用之和：

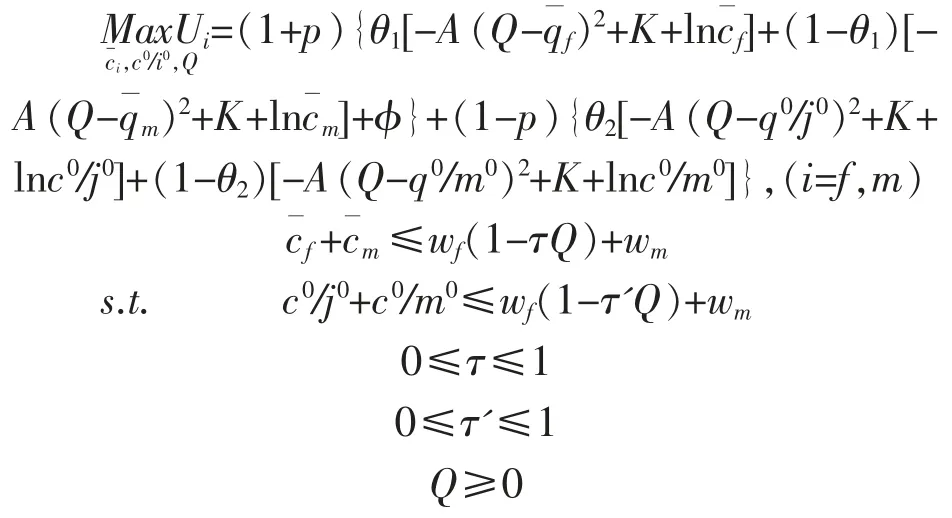
构造拉格朗日函数：

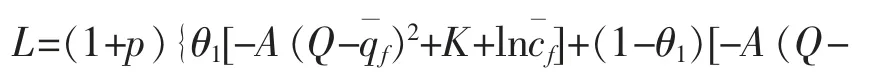
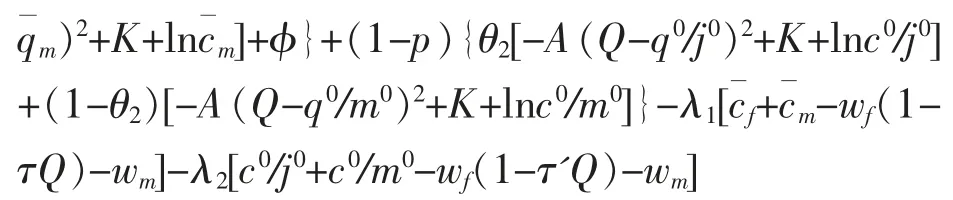
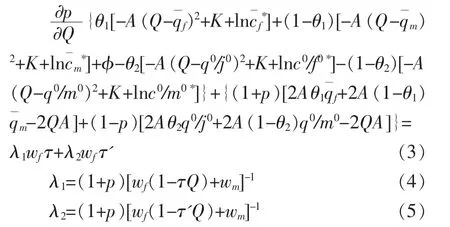
方程（3）左边第一项表示多生育一个孩子对婚姻稳定概率的边际影响所带来的边际效用，左边第二项表示婚姻稳定概率不变条件下多生育一个孩子带来的直接边际效用， 方程右边表示多生育一个孩子带来边际成本， 当生育孩子的边际效用等于边际成本时，即是最优生育数量。

（1）模型的均衡解

联合方程（1）、（2）、（3）、（4）、（5）可以解得均衡时的生育数量Q*和婚姻稳定概率p*，最优生育数量是关于一系列外生变量的函数，

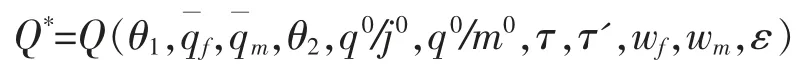
当生育率偏离均衡，例如生育率低于均衡时，增加生育数量会提高婚姻稳定性， 婚姻稳定性增强又提高生育数量， 生育率和婚姻稳定性都将上升直至达到均衡水平。

（2）比较静态分析

下面通过比较静态分析外生变量如何影响最优生育率Q*， 例如ε 变化对Q*的影响。 由方程（1）、（2）、（3）、（4）、（5）以及可以解得：

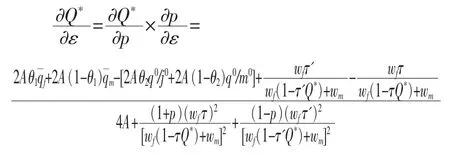
（3）p=0 和1 时的生育率比较

对第二期在婚家庭和离婚家庭生育率进行比较，以进一步验证上述结论。当第二期婚姻稳定性p=1 时， 家庭决策的目标是在联合约束下最大化经过加权的集体效用：

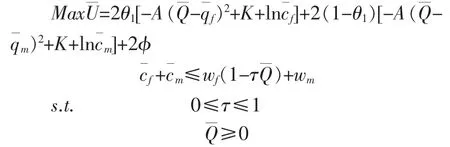
构造拉格朗日函数：

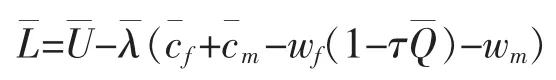
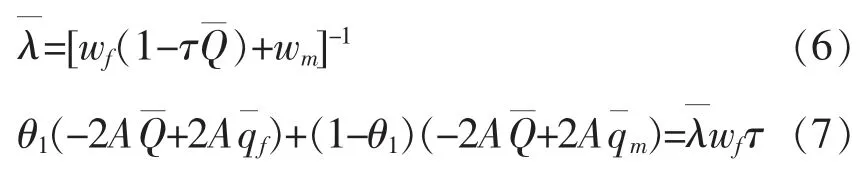
将（6）式代入（7）式得到：

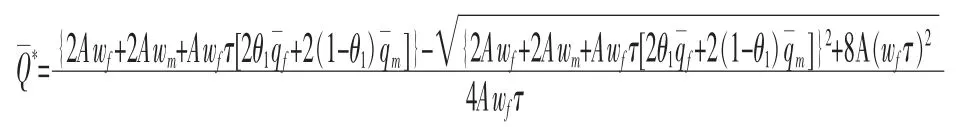
同理可以得到， 婚姻稳定性p=0 的家庭最优生育率解为：

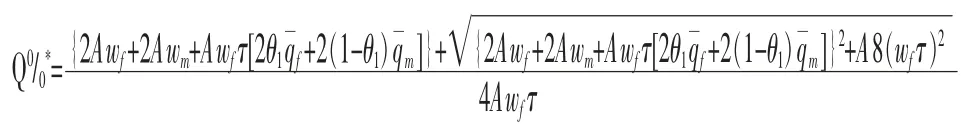
3.模型结论

基于以上分析，本文可以得到如下结论：

结论一：当其他外生因素不变时，婚姻稳定性和生育率会自动调节到一个稳定的均衡状态而不发生改变。

结论二：如果男女在婚时的理想生育数量大于离婚时的理想生育数量， 当有利于婚姻稳定性的外生因素减弱或不利于婚姻稳定性的外生因素增强时，生育率下降。

推论：如果男女在婚时的理想生育数量大于离婚时的理想生育数量， 在婚家庭的生育率总是大于离婚家庭的生育率。

四、计量模型和数据分析

1.数据来源和变量选取

本文使用的数据来源于2010 和2013年中国综合社会调查（CGSS），选取15-60 岁农业户籍曾婚育龄人口作为研究样本③。为了检验婚姻稳定性对生育率的影响， 需要找到测量婚姻稳定性的变量。 已有的文献将婚姻状况或夫妻对婚姻质量的看法作为衡量婚姻稳定性的变量 （Koo and Janowitz, 1983; Lillard and Waite, 1993； Myers,1997; Rijkenand Liefbroer, 2009）。 本文使用的调查数据中包含受访者婚姻状况， 可以作为衡量婚姻稳定性的变量之一。 由于调查没有问及受访者对婚姻质量的看法，尝试寻找其他变量。首先该调查询问了受访者关于“两性关系过度开放导致婚姻不稳定” 严重程度的看法，2.04%认为该问题非常不严重，19.83%认为比较不严重，43.68%认为严重程度一般，27.42%认为比较严重，7.03%认为非常严重。 可见公众普遍认为两性关系过度开放是影响婚姻稳定性的不利因素。那么对待性行为（特别是婚外性行为）的态度会影响婚姻稳定性，受访者对婚外性行为越认同，其婚姻稳定性可能越低，离婚的可能性越大。 该调查询问了受访者对于婚前性行为和婚外性行为的认可程度， 将婚外性行为和婚前性行为的认可程度分为5 类，“认为总是不对的”记为1，“认为多数情况下是不对的”记为2，“认为说不上对不对”的记为3，“认为有时是对的”的记为4，“认为总是对的”记为5。为了说明对待性行为的态度确实影响婚姻稳定性， 可以先采用计量回归方法检验婚前性行为和婚外性行为态度对离婚概率的影响，假设离婚方程为：

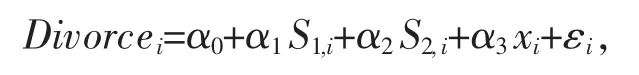
Divorcei表示受访者i 的婚姻状况，Divorcei=1代表离婚，Divorcei=0 代表未离婚（包括初婚和分居未离婚）；S1,i表示i 对婚外性行为的认可程度，S2,i表示i 对婚前性行为的认可程度；xi表示其他影响离婚率的因素；εi是随机扰动项α0、α1、α2、α3是待估参数。 则离婚的概率方程可表示为：

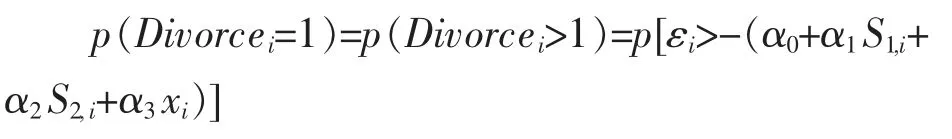
若婚外性行为（或婚前性行为）的认同程度与离婚概率存在显著正向关系，则可以认为，越认同婚外性行为（或婚前性行为）的受访者婚姻稳定性越低。

2.计量模型设定和数据描述统计

假设生育率方程如下：

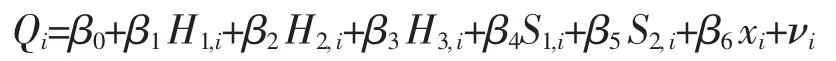
Qi表示受访者i 的子女数量，Hi表示婚姻状况，S1,i表示对婚外性行为的认可程度，S2,i表示对婚前性行为的认可程度，νi是随机误差项。Xi表示影响生育的一系列控制变量， 分为外生控制变量和可能内生的控制变量两类。 外生控制变量主要有受访户主的年龄、性别等，可能内生的控制变量主要有受访户主的教育水平、健康状况等，这些因素可能同时影响生育率和婚姻稳定性， 从而影响估计结果，比如初婚年龄越早，生育率应该越高，且初婚年龄越早， 可能意味着婚姻的搜寻时间过短，信息不对称越严重，离婚率越高。在回归中，通过依次加入外生控制变量和可能内生的控制变量，可以检验估计结果的稳健性。

表1 给出了样本主要变量的统计值， 观测样本的平均子女数量为1.65 个，平均理想生育数量为1.99 个，对婚外性行为的平均认可程度为1.26分， 对婚前性行为的平均认可程度为1.84 分；分居未离婚人口占0.4%，离婚人口占1.4%，再婚人口占1.8%， 剩下的为初婚人口； 男性人口占47.5%， 少数民族人口占11.2%， 不信教人口占87.8%， 平均初婚年龄为22.8 岁， 平均年龄为41.36 岁，平均受教育程度为7.7年，平均个人年收入为1.58 万元，平均健康程度为3.78 分。

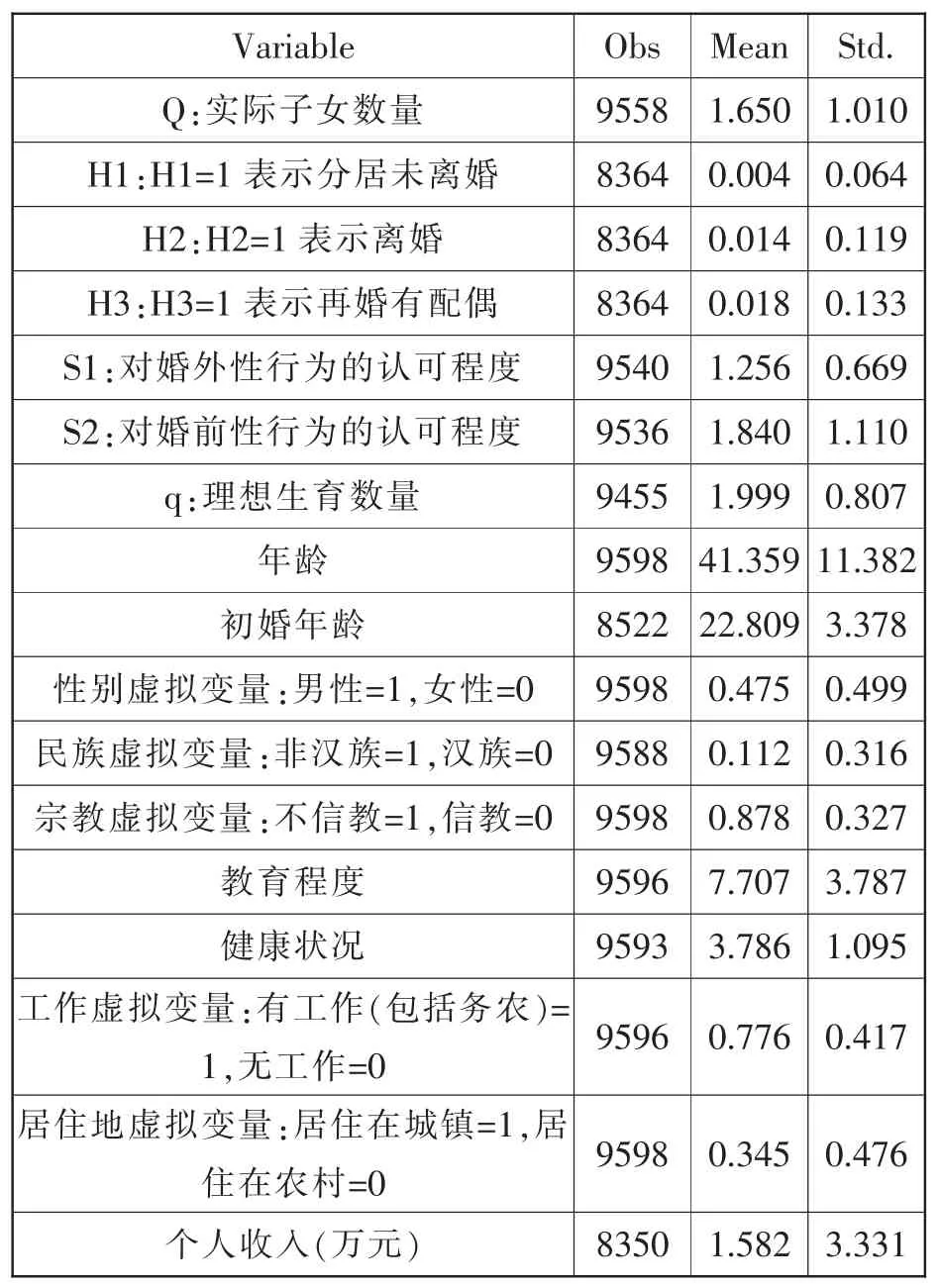
表1 主要变量的统计值

3.数据分析

表2 反映了不同婚姻状况下的受访者的理想生育数量，总样本中初婚者、分居未离婚者、离婚者和再婚者的平均理想生育数量分别为2.03、1.97、1.69 和2.16 个。 与初婚者相比，分居未离婚者的理想生育数量略下降； 离婚者的理想生育数量下降了0.34 个，且在1%水平上显著；再婚者的理想生育数量上升了0.13 个，且在10%水平上显著。 女性初婚者、分居未离婚者、离婚者和再婚者的平均理想生育数量分别为1.99、2.27、1.66 和2.08 个，男性初婚者、分居未离婚者、离婚者和再婚者的平均理想生育数量分别为2.08、1.79、1.72和2.24 个。 与女性初婚者相比，女性离婚者的理想生育数量下降了0.33 个，且在1%水平上显著；女性再婚者的理想生育数量上升了0.09 个。 与男性初婚者相比， 男性离婚者的理想生育数量下降了0.36 个，且在1%水平上显著；男性再婚者的理想生育数量上升了0.16 个。 总之，不管男性还是女性，离婚者的理想生育数量都显著低于初婚者。

表3 反映了不同婚姻状况下的受访者子女数量，总样本中初婚者、分居未离婚者、离婚者和再婚者的平均子女数量分别为1.82、1.92、1.18 和2.31 个。与初婚者相比，分居未离婚者的子女数量变化不显著； 离婚者的子女数量减少了0.64 个，且在1%水平上显著； 再婚者的子女数量增加了0.49 个，且在1%水平上显著。女性初婚者、分居未离婚者、 离婚者和再婚者的平均子女数量分别为1.80、2.17、1.29 和2.5 个，男性初婚者、分居未离婚者、 离婚者和再婚者的平均子女数量分别为1.83、1.80、1.08 和2.12 个。 与女性初婚者相比，女性离婚者的子女数量下降了0.51 个， 且在1%水平上显著；女性再婚者的子女数量增加了0.7 个。与男性初婚者相比， 男性离婚者的子女数量下降了0.75 个，且在1%水平上显著；男性再婚者的子女数量增加了0.29 个④。 总之， 不管男性还是女性，离婚者的生育数量显著低于初婚者。

表2 和表3 的统计结果表明， 离婚男女的理想生育率低于在婚男女性， 离婚男女性的实际生育率也低于在婚男女性，从而验证了3.3 的推论。

五、实证分析

1.对待性行为的态度对离婚率影响的回归结果

首先采用probit 模型对离婚概率方程进行回归，以检验对待性行为的态度对离婚率的影响。表4 第1 列只考察受访者婚外性行为和婚前性行为认同程度对离婚率的影响， 第2 列控制了受访者年龄、初婚年龄、性别、民族、宗教和调查年份，第3 和4 列进一步控制了受访者教育程度、 健康状况、工作状况、收入、居住地类型和省份虚拟变量。第1-3 列是基于所有观测对象的回归结果， 第4列是基于15-60 岁农业户籍曾婚育龄人口的回归结果。 第1 列回归结果显示，S1 项系数为0.0036，在1%水平上显著，表明受访者对婚外性行为的认同程度每增加1 单位，离婚概率将上升0.0036。第2 列和第3 列回归结果显示， 在逐步控制住其他变量后，S1 项依然显著为正， 第4 列针对15-60岁农业户籍曾婚育龄人口的回归结果也显示S1项系数显著为正，表明回归结果较为稳健，对婚外性行为的认同程度与离婚率存在显著正向关系。第1-4 列回归结果显示，S2（对婚前性行为的认同程度）项系数均不显著为正，表明受访者对婚前性行为的认同程度对离婚概率的影响是正向的，但不显著。 根据表4 的回归结果，可以得到，个人对婚外性行为的认同程度在一定程度上测量了婚姻的稳定程度。越认同婚外性行为，说明发生婚外情的概率越大，对婚姻的冲击越大，婚姻稳定性越低。

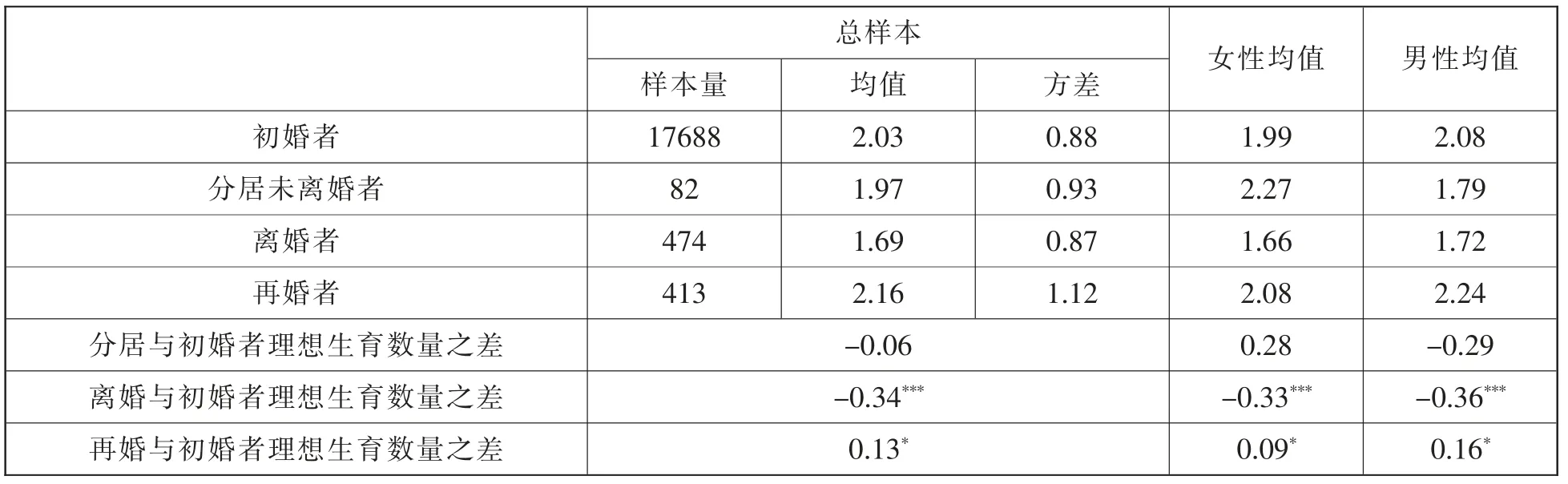
表2 婚姻状况与理想生育数量的关系

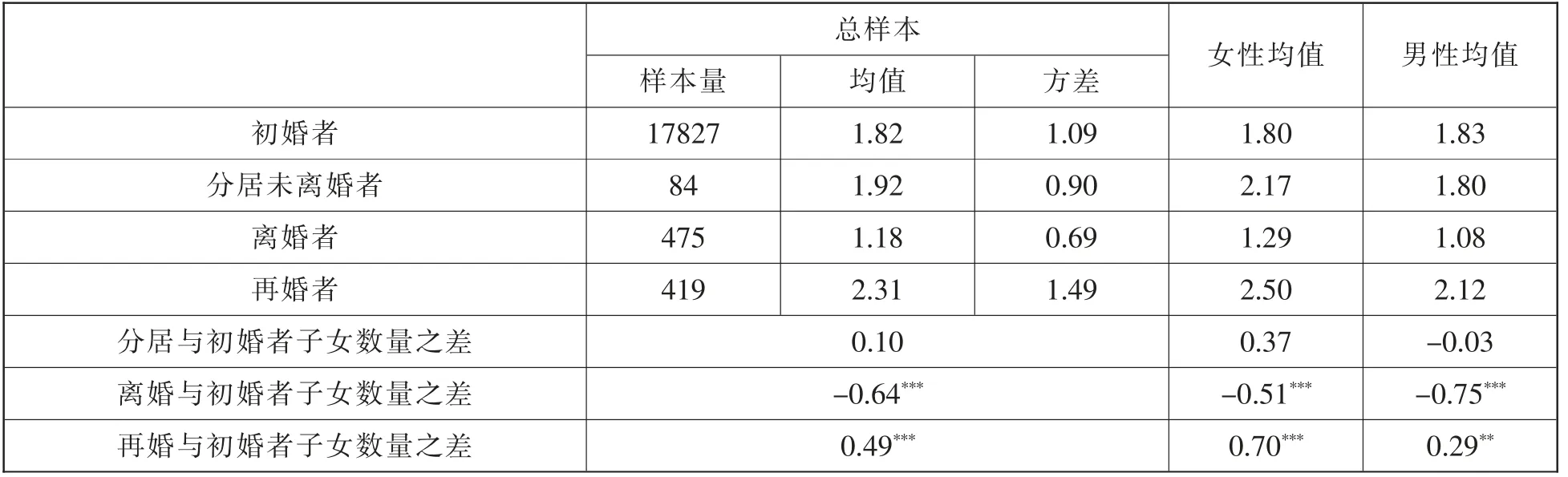
表3 婚姻状况与子女数量的关系

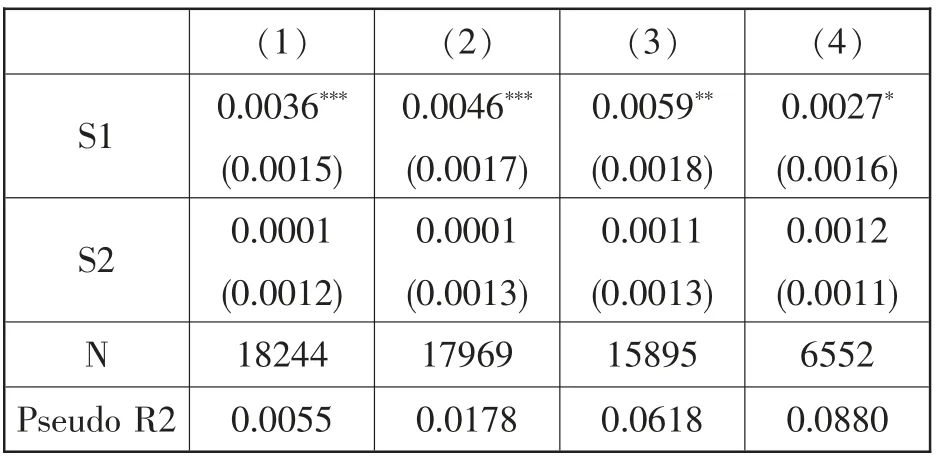
表4 对待性行为的态度对离婚率的影响

2.婚姻稳定性对生育率影响的回归结果

首先根据图1 反映的婚外性行为认同感与子女数量关系来初步分析婚姻稳定性对生育率的影响。 图1-（1）中，纵坐标表示受访者对婚外性行为认同值， 横坐标表示与相应认同值对应的平均子女数量。 S1=5 组的平均子女数量为1.08 个，S1=4组的平均子女数量为1.11 个，S1=3 组的平均子女数量为1.23 个，S1=2 组的平均子女数量为1.3个，S1=1 组的平均子女数量为1.79 个。 该图说明对婚外性行为的认同程度越高， 平均生育子女数量越少，意味着婚姻稳定性越低，生育率越低。 但是， 对婚外性行为持有不同态度的群体之间本身若存在生育意愿上的差异， 生育意愿又影响生育率， 那么各组生育率差异就有可能是生育意愿不同造成的， 而不一定是婚姻稳定性差异所致。 图1-(2)反映了受访者对婚外性行为认同程度与生育数量缺口⑤之间的关系，S1=1 组的平均子女数量比理想生育数量少0.29 个，S1=2 组的平均子女数量比理想生育数量少0.63 个，S1=3 组的平均子女数量比理想生育数量少0.68 个，S1=4 组的平均子女数量比理想生育数量少0.93 个，S1=5 组的平均子女数量比理想生育数量少1.31 个。 该图表明随着个体对婚外性行为的认同程度增加， 生育数量缺口增大，由此可以说明图1-（1）中各组生育率差距并不是理想生育数量的差异造成的， 个体对婚外性行为的认同程度增加意味着婚姻稳定性降低，生育率随之下降。

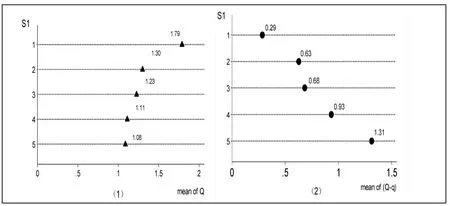
图1 婚外性行为认同感与子女数量的关系

下面利用15-60 岁农业户籍曾婚育龄人口样本对生育率方程进行回归， 检验婚姻稳定性对生育率的影响。 表5 第1-3 列采用异方差稳健标准差的OLS 回归方法，第4 列采用聚类稳健标准差的OLS 回归方法。 第1 列只考察受访者婚姻状况和对待性行为的态度的影响， 第2 列控制了受访者年龄、初婚年龄、性别、民族、宗教和调查年份，第3 和4 列进一步控制了受访者教育程度、 健康状况、工作状况、收入、居住地类型、理想生育数量和省份虚拟变量。 第1 列回归结果显示，H2 项系数为-0.646，在1%水平上显著，表明相比初婚者，离婚者的生育率下降了0.646 个。 H3 项系数为0.277，在5%水平上显著，表明再婚者相比初婚者的子女数量增加了0.277 个⑥。 S2 项系数为-0.109，在1%水平上显著，表明对婚前性行为的认同程度每增加1 单位，子女数量将减少0.109 个。S1 项系数为-0.0307，在10%水平上显著，表明对婚外性行为的认同程度每增加1 单位， 子女数量将减少0.0307 个。 第2-4 列回归结果显示，在控制住其他影响生育率的因素后，H2 项系数依然显著为负， 即离婚者的生育率低于初婚者；S1 项系数依然显著为负， 即对婚外性行为的认同程度增加使得生育率降低。 在逐渐增加控制变量后，H2和S1 的回归系数没有发生显著变化，说明回归结果较为稳健，表明随着婚姻稳定性下降，家庭生育率降低。

3.婚姻稳定性影响生育率的内生效应和外生效应

尽管表5 的回归结果表明婚姻稳定性对生育率存在总体的正向效应， 但这种效应可能是生育率的反向影响导致的。下面，本文考虑将人口流动作为婚姻稳定性的外生冲击， 通过比较农村流动人口和非流动人口婚姻稳定性与生育率的变动关系来试图识别婚姻稳定性影响生育率的内生效应和外生效应。

首先对回归样本进行重新筛选， 分析调查数据发现，40-60 岁农业户籍人口的子女平均年龄较大，且不与子女居住在一起的比例较高。这说明40-60 岁农业流动人口的子女出生较早， 虽然当前处于流动状态， 但在其子女出生前或出生期间并不一定处于流动状态， 其流动与否对生育率的影响并不明显， 因此本文利用15-39 岁农业户籍曾婚人口样本进行研究。根据理论分析，当其他外生因素不变时， 由于婚姻稳定性与生育率之间相互影响，两者达到一个均衡的稳定状态。当影响婚姻稳定性的不利外生因素增加时， 生育率是下降的。已有的研究发现，人口流动对婚姻稳定性具有负的外生冲击（风笑天，2006；杜凤莲，2010；高梦滔，2011 等），预期这种冲击会对生育率产生局部均衡影响。

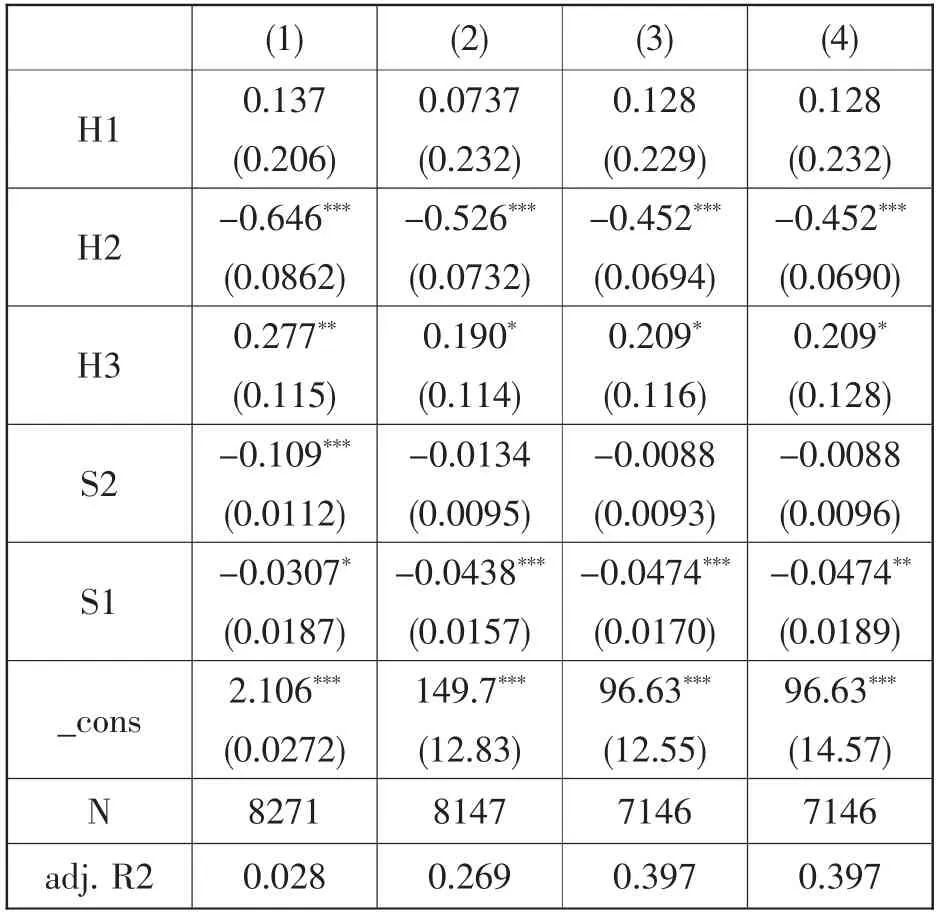
表5 婚姻稳定性对生育率的影响

在生育率方程中分别加入流动和S1 的交互项、流动和S2 的交互项进行回归。 表6 第1-3 列显示了流动与S1 的交互效应。 第1 列只考察S1项与交互项L*S1，结果显示S1 项系数不显著，交叉项L*S1 系数均显著为负。这表明农业非流动人口对婚外性行为的认同程度不会影响生育率，农业流动人口对婚外性行为的认同程度对生育率具有显著负效应。 第2 列在第1 列的基础上加入受访者年龄、初婚年龄、性别、民族等相对外生的控制变量， 第3 列在第2 列的基础上加入了受访者教育水平、 健康状况等可能内生的控制变量和省份虚拟变量，结果都显示S1 项系数不显著，交叉项系数依然显著为，说明回归结果比较稳健。农业非流动人口对婚外性行为的认同程度不会影响生育率，这是因为在其他外生因素不变的情况下，婚姻稳定性与生育率之间的多重反馈机制使得两者处于一个稳定的均衡状态。具体分析过程如下：农村非流动人口对婚外性行为的认同程度增加，一方面可能导致婚姻稳定性降低进而不利于生育数量增加， 另一方面生育数量增加反过来有利于提高婚姻稳定性从而有利于生育率上升， 因而非流动人口的生育率均衡在没有外生因素作用下将保持不变。 农业流动人口对婚外性行为的认同程度增加会使得生育率显著降低，这是因为，人口流动对婚姻稳定性具有负的外生影响， 当影响婚姻稳定性的不利外生因素增强时， 生育率就会下降到一个更低的均衡水平。

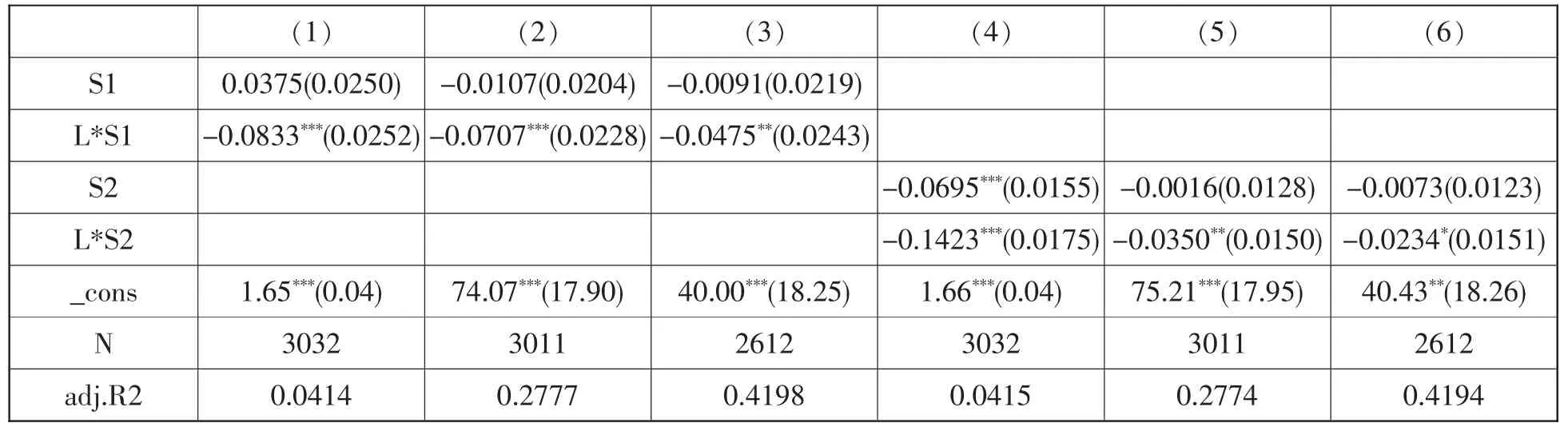
表6 人口流动对生育率的局部均衡影响

表6 第4-6 列显示了流动与S2 的交互效应。第4 列只考察S2 项与交互项L*S2，第5 列在第4 列的基础上加入受访者年龄、 初婚年龄、性别、 民族等相对外生的控制变量， 第6 列在第5列的基础上加入了受访者教育水平、健康状况等可能内生的控制变量和省份虚拟变量，结果都显示交叉项系数显著为负，表明当不利于婚姻稳定性的外生因素增强时，生育率下降。 表6 的回归结果在一定程度上验证了本文3.3 的结论， 表明婚姻稳定性对生育率的影响存在内生效应和外生效应。

六、结论

据2015年全国1%人口抽样调查显示， 我国2015年的总和生育率仅为1.05， 远远低于2.2 的更替水平。 实施全面二孩政策以后，2016年全国出生人口总量为1618 万，低于2015年的1655 万和2014年的1687 万， 我国的低生育率现象依然突出。造成生育率低下的原因有很多，其中婚姻稳定性是一个不可忽略的重要因素。 目前国内在这方面的研究还很缺乏， 本文在考虑生育率与婚姻稳定性相互影响的基础上， 分析了婚姻稳定性与生育率变动的关系。在理论方面，将婚姻稳定性分为受生育率影响的内生部分和不受生育率影响的外生部分，构建生育模型分析得到：在其他外生条件不变的情况下，婚姻稳定性和生育率处于一个稳定的均衡状态而不发生改变；若男女在婚时的理想生育数量大于离婚时的理想生育数量，当影响婚姻稳定性的不利外生因素增强时，生育率下降。

在实证方面， 采用CGSS 微观调查数据检验婚姻稳定性对生育率的影响效应， 其中婚姻稳定性变量从受访者的婚姻状况和对待性行为的态度两个角度衡量。 回归结果表明婚姻稳定性对生育率具有总体正向效应， 具体则表现为农村非流动人口婚姻稳定性对生育率没有显著影响， 而流动人口婚姻稳定性对生育率具有显著正向影响。 这是因为非流动人口没有受到外生因素冲击， 生育率和婚姻稳定性都处于均衡水平而不发生变化；流动人口则受到不利于婚姻稳定性的外生因素影响，使得均衡的生育率和婚姻稳定性水平都降低。本文得出的政策启示是， 应当增强有利于婚姻稳定性的外生因素， 使得社会生育率和婚姻稳定性都提升到一个较高均衡水平。

需要说明的是，由于数据的限制，本文的实证分析只是初步识别了婚姻稳定性影响生育率的内生效应和外生效应， 实证的数据和方法都有待改进。 未来，在获取适当数据的基础上，还需要作进一步严格的分析。

注释：

①下标f 表示女性，m 表示男性；A、K 为大于0 的 常数，Fi（Q）是关于的倒“U”型函数，Q 与越接近，Fi（Q）越大， 即实际生育数量越接近理想生育数量时效用越大；表明生育数量和消费数量均满足边际效用递减性质。

③曾婚人口包括初婚者、分居未离婚者、离婚者、再婚者。

④对于初婚者和离婚者而言，子女数量基本上等同于实际生育数量；对于再婚者而言，由于包含了继子和继女，子女数量可能大于实际生育数量。

⑤生育数量缺口指的是实际子女数量与理想生育数量之差的绝对值。

⑥再婚者子女数量增加的原因可能有两个，一是生育行为导致，已有的研究表明，已有子女的再婚家庭往往希望生育共同的孩子来达成联合承诺（Vikat et al.，1999；Buber&Prskawetz，2000；Prskawetz et al.，2002 等），二是继子女数量增加导致。