半盲二维自聚焦SAR运动目标成像方法

贺雪莉， 王晨沁， 毛新华

(南京航空航天大学电子信息工程学院， 江苏南京 211106)

0 引言

合成孔径雷达(SAR)是一种相干成像系统，其中距离向高分辨率通过对宽带信号进行脉冲压缩处理得到，而方位向高分辨率则通过对合成孔径数据进行相干处理实现，这种相干处理依赖于精确获知雷达和目标之间的瞬时相对位置信息。对于固定的场景，这些信息通常可以通过运动传感器得到，例如GPS和IMU。然而，对于运动目标而言，由于目标的非合作运动，几何关系具有不确定性。经典的SAR处理可以对静止场景提供精确的相干处理，而运动目标则会在SAR成像处理中出现散焦。

由于目标的运动对SAR信号会产生两个方面的影响，一是会在方位向引入一个相位误差，导致图像发生方位散焦，二是会产生额外的距离徙动，在SAR成像过程中无法得到补偿，而且经过成像算法处理后，残留距离徙动效应还会导致图像距离向出现二次散焦，因此在成像过程中，必须精确估计和校正距离徙动和方位相位误差[1-2]。

方位相位误差的估计一般使用常规自聚焦算法(典型算法如子孔径算法、相位差分算法、相位梯度自聚焦算法、特征值方法等)实现。对于距离徙动，Keystone变换(KT)是当前运用最广的一种方法，它可以在没有目标运动信息的情况下校正距离向的线性走动，但是Keystone变换不适用于信号存在多普勒模糊的情况，且忽略了高阶距离徙动。为了处理目标沿着任意路径运动的成像问题，逆合成孔径雷达(ISAR)[3]的方法被应用到了SAR动目标成像当中，但是在图像域，残余的二维相位误差不仅仅包含距离徙动和方位相位误差，还存在高阶相位误差。标准ISAR算法仍对二维相位误差分开估计，这不但使估计精度受限，而且计算更为复杂。

本文分析了PFA极坐标格式转换对运动目标回波相位信号的影响，得到了残留二维相位误差的精确解析结构。利用这种先验的解析结构信息，提出了一种基于一维估计/二维补偿的自聚焦算法，算法只需直接估计方位一维相位误差，然后利用先验知识将方位相位误差映射得到二维相位误差，从而完成二维相位误差的精确估计和补偿。

1 动目标相位误差模型

1.1 相位历史域信号模型

星载聚束SAR数据采集几何模型如图1所示，为简化分析，假定雷达沿平行于x轴的轨迹运动，则结论很容易推广到斜视情况。以雷达波束照射的场景中心O为原点建立XYZ坐标系，在该坐标系内雷达天线相位中心瞬时位置为(xa,ya,za)=[xa(t),ya(t),za(t)]，雷达天线相位中心(APC)到场景中心O的距离记为rc≡rc(t)，它对应的瞬时方位角和俯仰角分别记为θ≡θ(t)和φ≡φ(t)，将孔径中心时刻定义为方位时间的原点，并将其作为成像时的参考点，该参考点对应的方位角和俯仰角记为θ=0和φref，不失一般性，在星载聚束SAR的数据采集模型中海面目标的运动轨迹如图1的动目标Q所示。

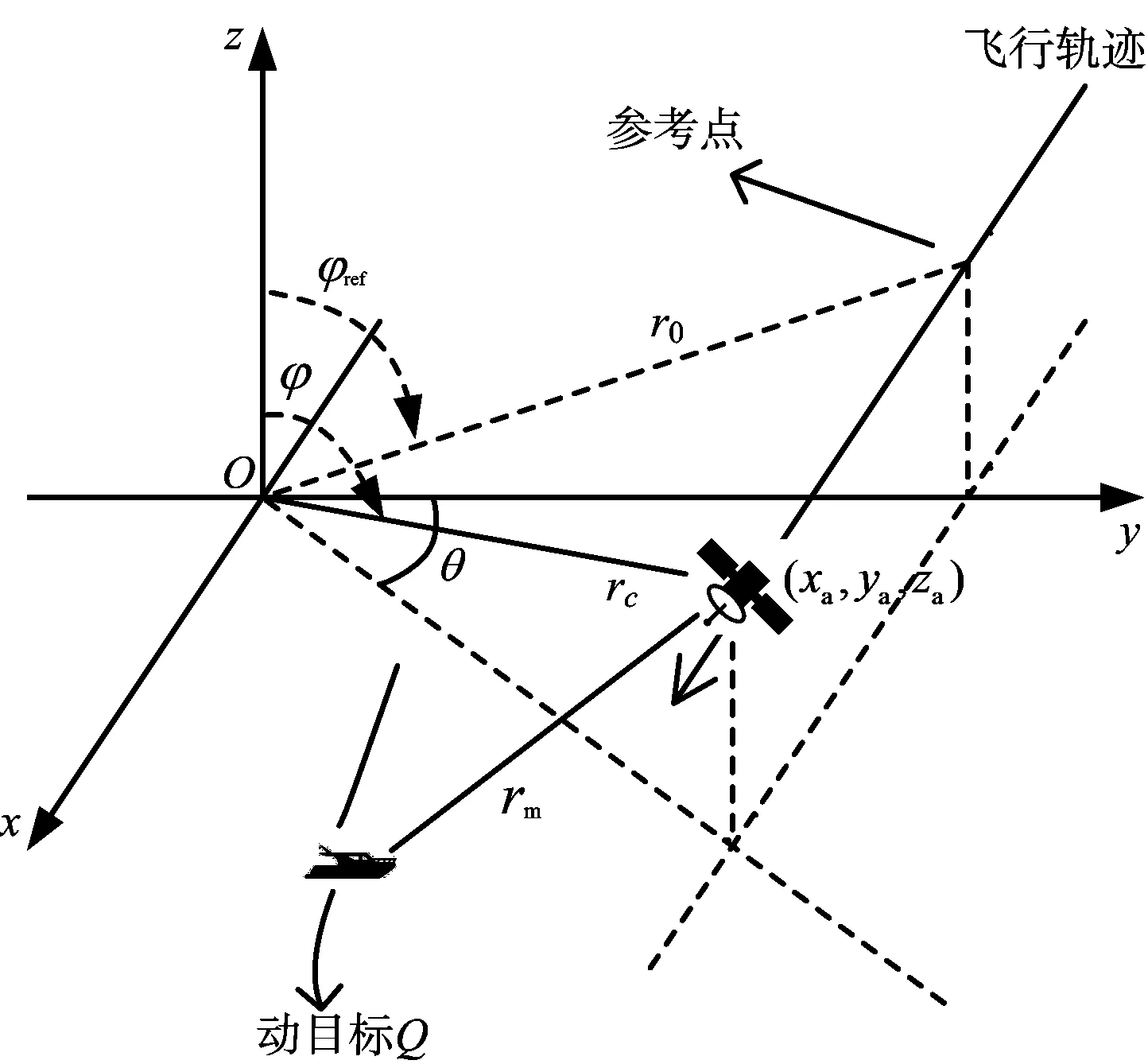
图1 聚束SAR数据采集几何模型

雷达发射宽带信号，被场景中点目标反射后接收到的回波信号通过解调、距离匹配滤波的预处理后可以表示为

(1)

式中，t为方位时间，fr为距离频域，fc为发射信号载频，c为电磁波传播速度，rm(t)为从雷达到运动目标的瞬时距离，A为回波信号的幅度。

从式(1)可以看到，在相位历史域，相位包含两个部分，一个是方位相位项，与距离频率无关，另一个是距离徙动项。显而易见，这两个部分成线性关系。

1.2 空间频率域相位误差模型

在基于SAR的运动目标检测与成像系统中，首先运用SAR成像算法，产生整个场景的合成图像。在SAR成像中，静止目标聚焦效果良好，而运动目标则由于二维相位误差出现散焦。为了补偿误差相位使运动目标也可以良好地聚焦，希望得到SAR图像运动目标的二维相位误差模型。下文将分析在极坐标格式算法(PFA)中的二维相位误差框架结构。

在PFA处理中，首先将回波信号运动补偿到参考点(一般情况下选择场景中心作为参考点)。如式(1)所示，rm(t)代表从雷达到运动目标的瞬时距离，运动补偿后，信号变为

SA1(t,fr)=SR[ϑa(t),fr]=

(2)

在文献[4]中给出了极坐标格式转换的一种新的解释，把距离重采样理解为距离频率的尺度变换，方位重采样理解为RCM线性化和Keystone变换的组合。

距离重采样即距离频率的尺度变换包含一个缩放因子δr=sinφref/(sinφcosθ)和一个偏移量fc·(δr-1)，距离重采样后，式(2)变为

SR(t,fr)=SM[t,fr+fc(δr-1)]=

(3)

式中，ϖ(t)=[rc(t)-rm(t)]/(sinφcosθ)。

PFA的第二步是方位项重采样，分为RCM线性化和Keystone变换两步进行，RCM线性化是一种方位时间的转变，与距离频域互相独立，使tanθ线性化。在数学上，这个过程可以在方位时间域进行变量代换，使t→ϑa(t)，则RCM线性化后，式(3)变为

(xa,ya,za)=[xa(t),ya(t),za(t)]

(4)

式中，η(t)=ϖ[ϑa(t)]为关于方位时间t的函数，泰勒展开后得

η(t)=a0+a1t+ξ(t)

(5)

式中，a0为常数项，a1为线性项系数，ξ(t)为二次及高阶项。

极坐标格式转换的最后一步是对式(4)进行Keystone变换，得到

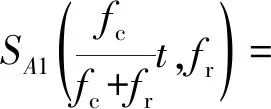
(6)

为与传统符号表达一致，定义

(7)

分别表示x轴和y轴的空间频域，距离频域存在偏置Y0=4πsinφreffc/c，将变量代入式(6)后，得到

(8)

在式(8)中，距离和方位频域的线性相位项系数表示了运动目标在SAR成像中的位置，耦合项

(9)

是需要被校正的二维相位误差。

1.3 残留相位误差结构分析

为了分析相位误差的结构，将式(9)在距离频域泰勒展开[5]，得

Φe(X,Y)=φ0(X)+φ1(X)(Y-Y0)+

φ2(X)(Y-Y0)2+…

3.气滞血淤。睾丸逐渐肿大、坚硬，疼痛轻微，舌暗边有淤斑、苔薄白，脉弦滑。治法：行气活血，散结。方药：橘核、木香、枳实、厚朴、川楝于、桃仁、延胡索各30 g，昆布、海藻各25 g，木通25 g，生地、元参、菊花、蒲公英各35 g，鹿含草30 g。湿热下注，发热恶冷，睾丸肿胀疼痛，质地硬，小便赤涩，大便干，舌红苔黄腻，脉弦滑数。治法：清利湿热，解毒消痈。方药：黄芩、栀子、木通、车前子、泽泻、当回、生地各30 g，柴胡25 g，甘草20 g，龙胆草25 g，金银花、川楝于各30 g。

(10)

式中，

(11)

(12)

(13)

ξ′(X/Y0)和ξ″(X/Y0)分别是ξ(X/Y0)的一阶和二阶导数。在式(10)中，φ0(X)是方位误差相位，φ1(X)是距离残留徙动，φ2(X)和其他高阶项均与距离向聚焦相关。

根据式(9)和式(11)可以得到

(14)

2 动目标聚焦成像

2.1 多普勒模糊校正

Keystone变换在不存在多普勒模糊的情况下可将线性走动项校直，但是当信号存在多普勒模糊的情况下，Keystone变换变得不再适用，若将式(5)中的线性项a1t用(p1+p2)t表示，其中，p1引起了整数倍的多普勒模糊，而p2不存在多普勒模糊，则经过Keystone变换后式(6)变为

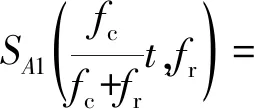
(15)

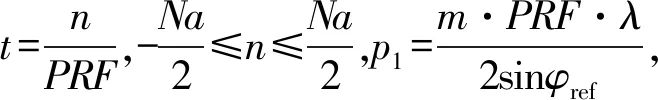
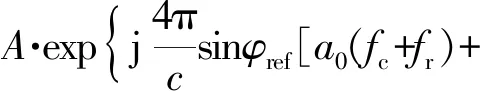
(16)

2.2 基于先验知识的动目标聚焦成像

在PFA中对动目标成像需要估计及校正式(9)中的二维相位误差，若没有二维相位误差结构的先验知识，在可以忽略距离向高阶误差时，可以用ISAR方法对方位误差相位和距离徙动分别盲估计，但是计算复杂，准确率不高。在上节分析后，知道在PFA处理后的二维误差相位有固定的内在结构。从式(14)可以看出二维误差相位可以从方位误差相位得出，只需估计方位相位误差，即可得出距离残余徙动。因此，基于先验知识的运动目标成像二维自聚焦方法工艺流程如图2所示。该算法的关键是由两部分组成：方位误差相位的估计和二维相位误差的计算。

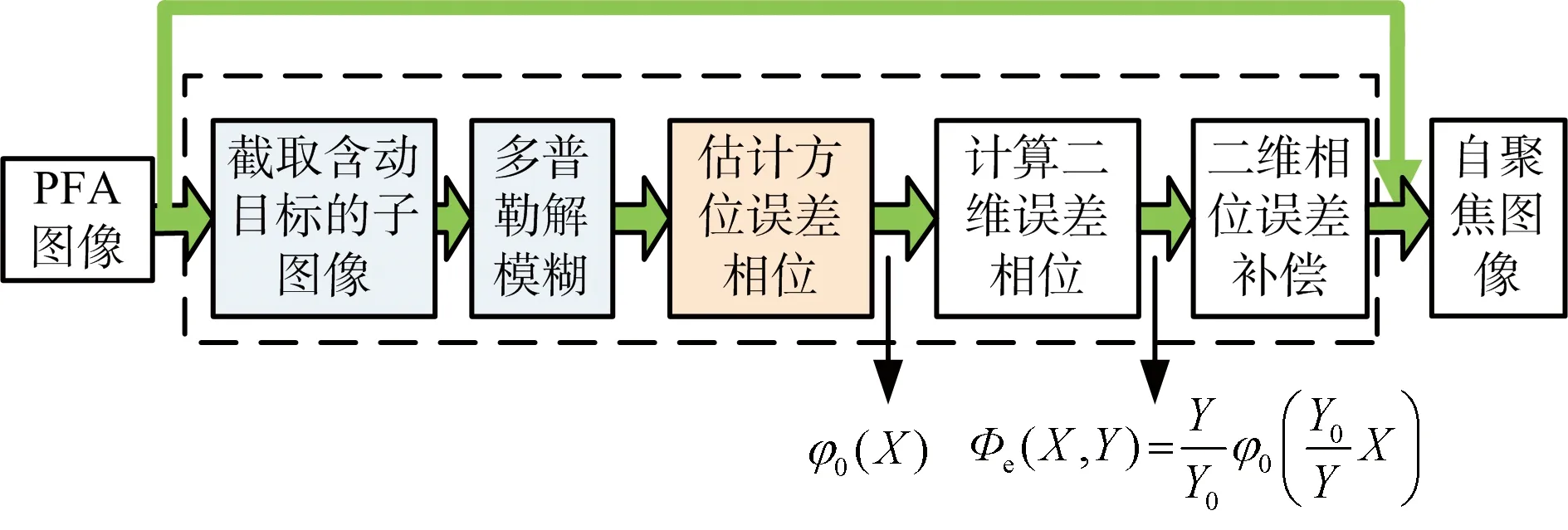
图2 二维自聚焦处理流程

对于方位相位误差的估计，可以利用常规的自聚焦算法完成，但如果在残留距离徙动不能忽略时直接应用这些方法，相位误差估计性能会受到很大影响。最直接的改进方法是估计前先将数据在距离向降分辨，使分辨率降低后残留距离徙动不超过一个分辨单元。这种改进方法在残留距离徙动跨距离单元数不多时能够很好地改善方位相位误差估计精度，但在误差特别大时，仍然存在一定的限制。首先，距离分辨率的降低，减少了可用于方位相位误差估计的距离独立样本数，而且分辨率降得越多，独立样本数变得越少，因此当残留误差特别大时，相位误差估计会由于独立样本太少而影响估计精度。其次，常规自聚焦算法在对大的相位误差进行估计时也表现出一定的局限性。为了克服上述问题，提出了基于子孔径的自聚焦算法。

首先，将极坐标格式转换后的数据在距离向分成多个子孔径，只要子孔径大小选取得合适，在子孔径内，不存在距离向徙动，利用常规自聚焦算法对各子孔径中的方位相位误差进行估计。然后利用映射关系求出各孔径相位误差在φ0(X)处的相位误差，求平均得到方位相位误差的估计值。其处理流程如图3所示。

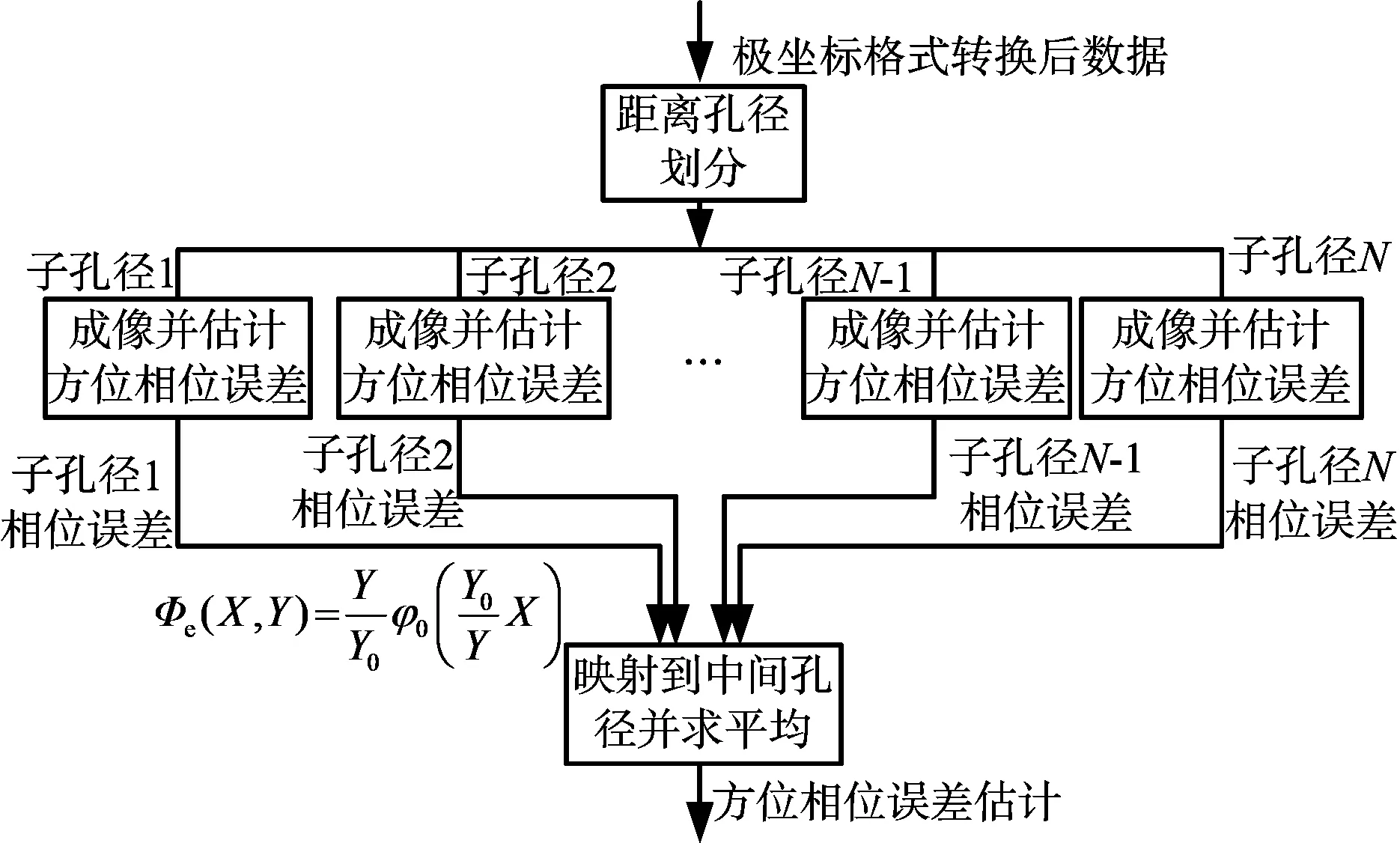
图3 基于子孔径的方位相位误差估计处理流程

有了方位相位误差的估计，根据式(14)就可以由该估计的一维相位误差直接计算得到二维相位误差。观察式(14)不难看出，该映射本质上是在每个距离频率上对方位相位误差做一个与距离频率有关的尺度变换，该尺度变换可通过插值完成，也可以通过变尺度原理实现。这种基于先验相位结构信息的降维估计方法不仅可以降低算法的计算复杂度，而且克服了传统二维自聚焦算法由于缺少冗余度而无法精确估计相位问题。

3 试验验证

3.1 仿真数据验证

在成像处理中，由于运动物体的运动速度及路线的不确定性，可能会出现方位向的多普勒模糊，这会急剧降低成像的质量。仿真过程中星载雷达主要参数如表1所示。

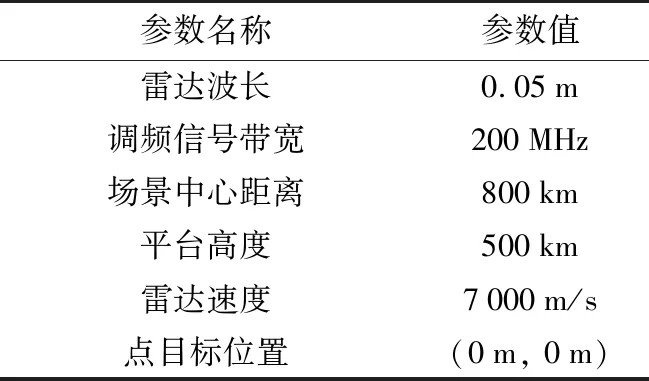
表1 仿真雷达参数

设置该点目标沿着x轴方向45°进行35 m/s的速度与5 m/s的加速度进行运动，并加入一定的正弦运动。

对在该仿真参数下的动目标回波数据直接进行PFA处理，处理结果如图4(a)所示，可以看到因为目标的不规则运动及多普勒模糊的存在，出现多普勒混叠及二维散焦，成像质量比较恶劣，看不出点目标的存在，需要在自聚焦前对成像结果进行进一步处理。

图4(b)是将该PFA动目标图像进行截取后完成多普勒解模糊，得到图像后再使用一维自聚焦处理(本文使用PGA方法)后得到，可以很明显地看到，经过了PRF的距离徙动校正及方位向的自聚焦，成像质量较PFA图像有了很大的改善，但由于距离向徙动的不可忽略，图像仍有明显的散焦。

(a) PFA成像图

(b) PGA结果图图4 PFA与一维自聚焦成像结果

本试验中将采取ISAR成像与本文所提到的

二维自聚焦方法对该动目标分别成像，成像结果如图5所示，为了更为直观，采用等高线作图，图5(a)是ISAR方法得到的最终成像结果，图5(b)是本文提出的基于先验知识的二维自聚焦方法得到的最终成像结果，可以清楚地看到，本文所使用方法可以得到更清晰完整的点目标成像结果。

(a) ISAR方法成像结果

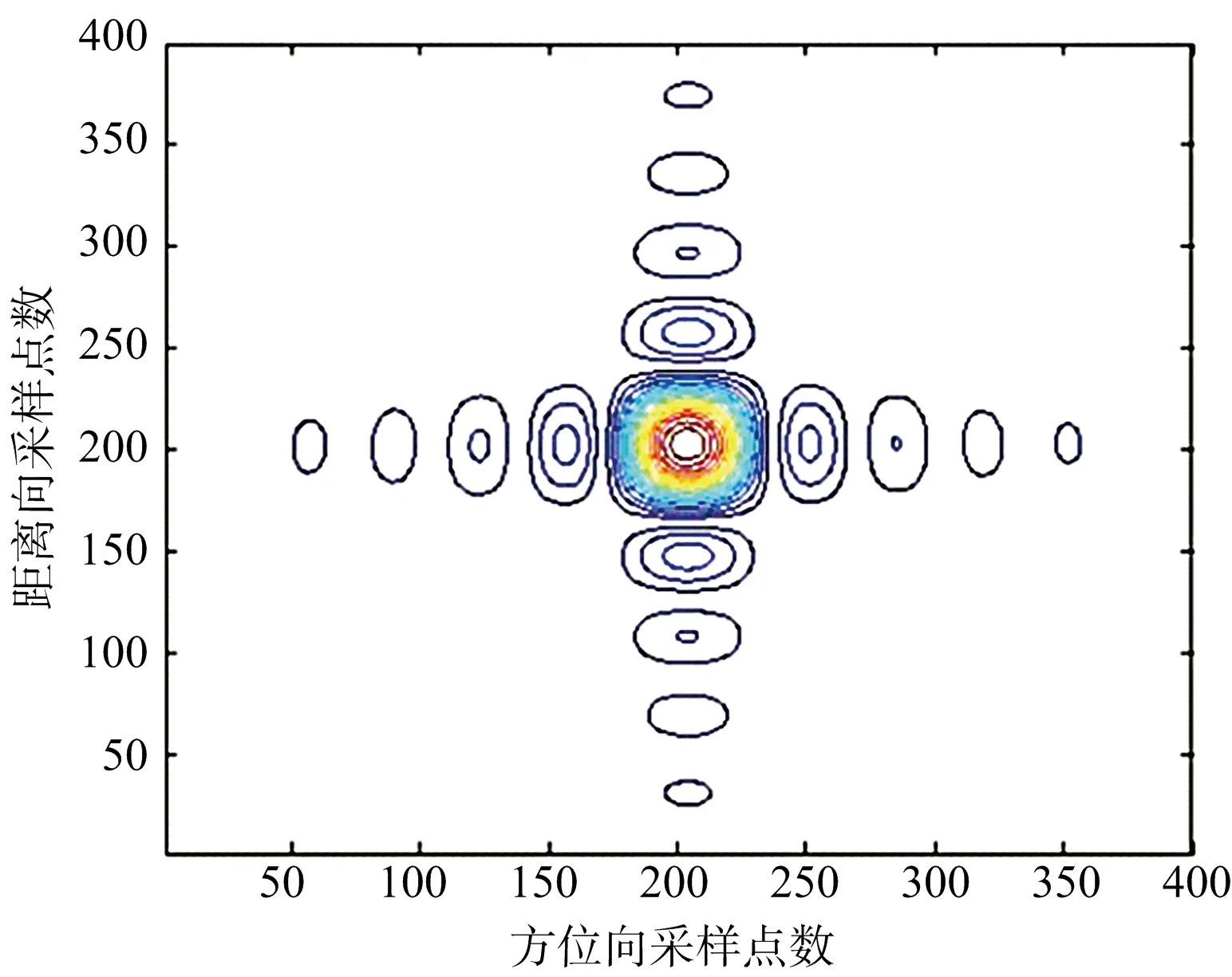
(b) 本文方法重聚焦结果图5 动目标成像结果

将两种方法的成像结果进行点目标分析后的结果如表2所示。根据表2的点目标分析参数可以看出，二维自聚焦方法在运行精度和时间上都占有优势，效果好于原来的动目标成像方法。

表2 两种算法的比较

3.2 实测数据验证

图6为实测数据成像结果，对该成像结果分别采用PGA, ISAR和本文所提到的二维自聚焦方法的成像结果分别如图7所示。从图中可以看出，PGA与ISAR方法虽然对成像质量有较大改善，但仍然存在明显的旁瓣，而本文所提出的二维自聚焦方法明显拥有较好的成像效果。根据图片，可以看到本文所使用的二维自聚焦方法虽然拥有较好的成像效果,但是由于实测目标的散射特性，所以可以看到成像结果仍存在一些散焦,等待进一步的研究来处理该问题。

图6 实测数据成像结果

(a) PGA成像结果

(b) ISAR成像结果

(c) 本文所提出二维自聚焦成像结果图7 基于不同处理算法的实测数据成像结果

图8 方位向频域信号成像结果

这3种方法的方位向频域信号如图8所示，由于目标运动引起的距离徙动是造成成像结果质量恶化的原因之一，所以成像方法能否补偿全距离徙动是衡量该成像方法好坏的标准之一。从图中可以看出，PGA方法无法将距离徙动全部补偿完全，仍然可以看到明显的距离徙动，图9是将图8中的ISAR方法和二维自聚焦方法两图放大后的图像，从该图像可以看出，ISAR方法距离对准后仍会存在距离向信号跳变的情况，但本文所提出的二维自聚焦方法由于补偿的相位为连续信号，所以补偿完后，已经看不到明显的距离徙动，所以该方法明显具有优势。

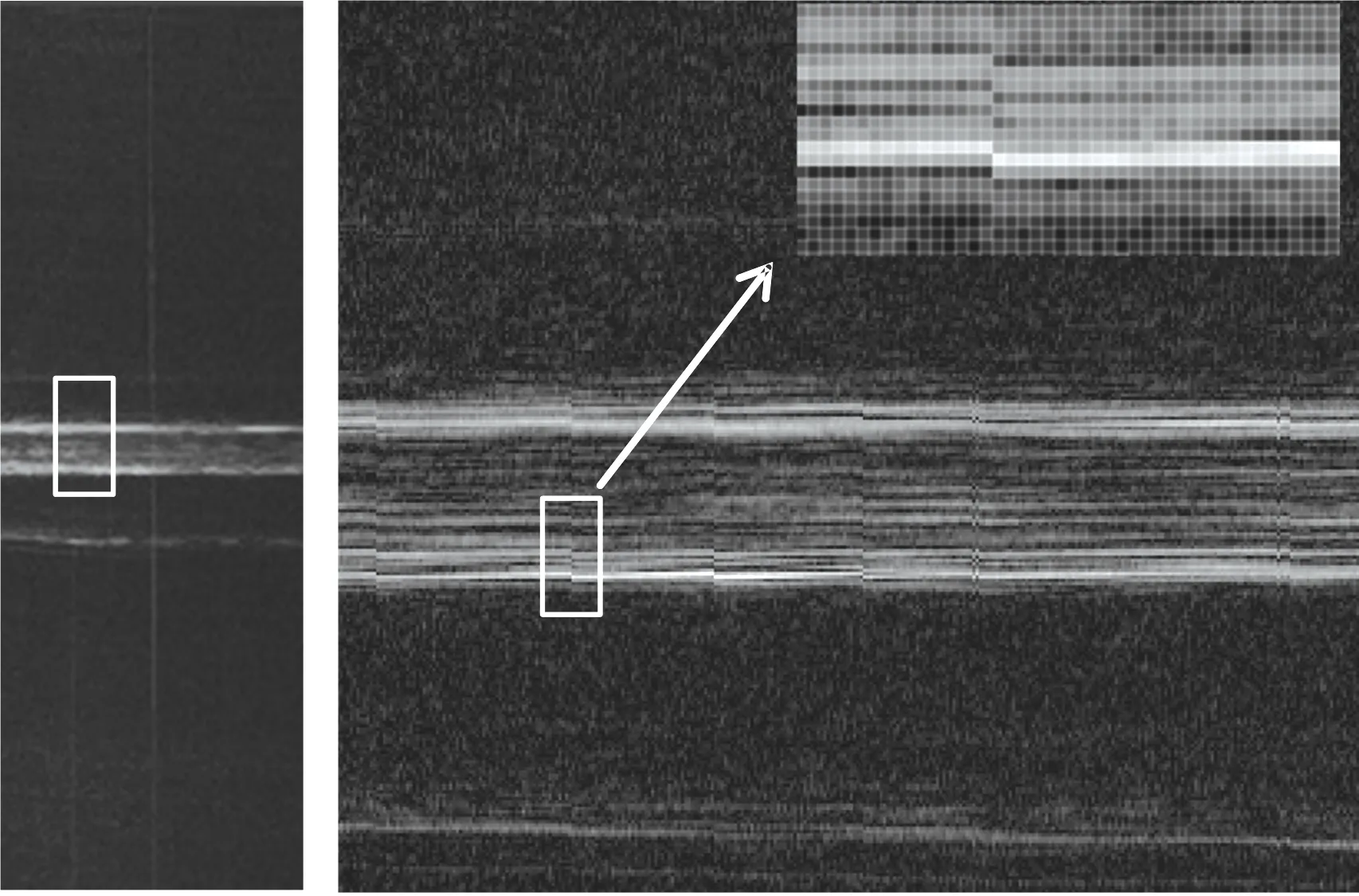
(a) ISAR方位向频域信号部分放大

(b) 本文所提出二维自聚焦方位向频域信号部分放大图9 图8的部分放大结果

4 结束语

本文以极坐标格式算法为例，详细分析了成像算法处理后残留二维相位误差的解析结构，并利用这种先验辅助知识，将二维相位误差估计问题转化为方位一维相位误差估计，提出了一种基于一维估计/二维校正的自聚焦算法。算法只需直接估计方位一维相位误差，然后利用二维相位误差内部所特有的结构信息，将一维相位误差映射得到二维相位误差，从而实现二维相位误差的精确估计和补偿。这种基于先验相位结构信息的降维估计方法不仅可以降低算法的计算复杂度，而且克服了传统二维自聚焦算法由于缺少冗余度而无法精确估计相位问题。虽然如此，本文还仅仅只是针对一种经典SAR成像算法，即极坐标格式算法进行了深入分析，考虑到不同成像算法处理后残留误差并不具备统一性，因此后续工作中有必要对其他算法的误差特性进行分析和比较，以进一步完善这种基于先验知识的二维自聚焦方法。