常系数线性微分方程解法研究的新认识

赵临龙

(安康学院数学与统计学院，陕西 安康 725000)

1 引言

对于常系数线性方程

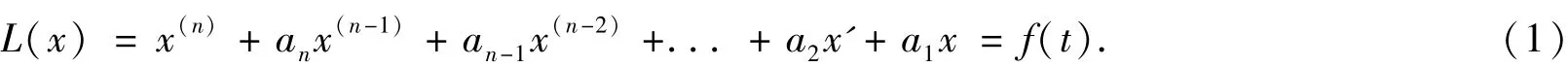
尽管理论上，已经知道方程(1)的解，由齐次方程L(x) ＝0 的通解与其非齐次方程L(x) ＝f(t) 特解的和构成.但在具体的解法中，已有常系数齐次方程L(x) ＝0 的通法，而对于非齐次方程L(x) ＝f(t) 的特解，函数f(t) 在什么条件下存在解，以及怎样求出其解，并没有给出具体的通法[1-12].因此，常系数线性微分方程的解法依然是未彻底解决的“世界难题”.

笔者在文献[13-14]中，对于常系数线性微分方程组的解法进行研究，得到相关结论.本文将在此基础上，对常系数线性非齐次微分方程解法进行深入讨论，针对函数f(t) 探讨常系数线性非齐次方程解存在的条件，并给出可解的常系数线性微分方程较普遍的解法.

2 方程组的解理论

对于常系数线性微分方程(1)，通过变换:

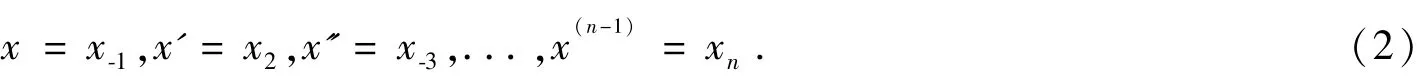
化为常系数线性微分方程组:

其常系数线性微分方程(1)与常系数线性微分方程组(3)的特征根不变.[15]

对于常系数线性齐次微分方程组(3)，有以下结论

定理1[13-14]如果常系数线性微分方程组(3)有n 个互异的特征根λ1，λ2，...，λn，而对应的线性无关的特征行向量为K1，K2，…，Kn，则(3)化为一阶线性微分方程

定理2[13-14]如果常系数线性微分方程组(3)有不同的特征根λ1，λ2，…，λm，其重数分别为n1，n2，…，nm，n1＋n2＋…＋nm＝n，而对应的线性无关的特征行向量为K1，K2，...，Km，则(3)化为一阶线性微分方程

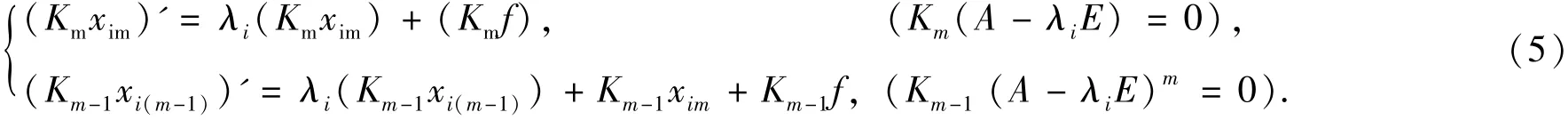
其中特征根λi对应特征行向量为Ki，xim、xi(m-1)为满足方程组(5)的递推解，i ＝1，2，...，m，对于自然数m 满足2 ≤m ＜n.

定理3 常系数线性微分方程(1)，通过变换(2)生成的常系数线性微分方程组(3)，有n 个互异的特征根λ1，λ2，...，λn，而且对应的线性无关的特征行向量为K1，K2，...，Kn，则积分(6)存在时，

方程组(3)化为一阶线性微分方程:

证明:对于常系数线性方程(1)在变换(2)下化为常系数线性微分方程组(3).

此时，若方程组(3)的特征根为n 个互异的特征根λi(i ＝1，2，...，n) ，对应的线性无关的特征行向量Ki＝(ki1，ki2，...，kin)(i ＝1，2，...，n) 满足

则有一阶线性微分方程:[13-14]

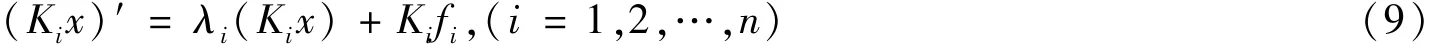
其中KI＝(ki，ki2，…，kin)，x ＝(x1，x2，…，xn)τ，f ＝(f1，f2，…，fn)τ，(i ＝1，2，…，n).显然，一阶线性微分方程(9)有形式:

即方程(9)在可积条件(6)下可解.定理1 获得证明.

定理4 常系数线性微分方程(1)，通过变换(2)生成的常系数线性微分方程组(3)，有不同的特征根λ1，λ2，...，λm，其重数分别为n1，n2，...，nm，n1＋n2＋... ＋nm＝n，而且对应的线性无关的特征行向量为K1，K2，...，Km，则当积分(11)和(12)存在时，

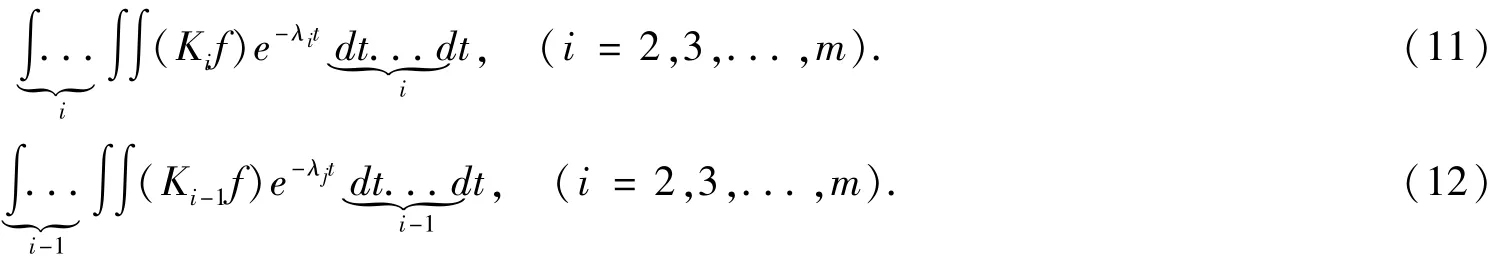
方程组(3)化为一阶线性微分方程:

其中特征根λi对应特征行向量为Ki，xim、xi(m-1)为满足方程组(13)的递推解，i ＝1，2，...，m，对于自然数m 满足2 ≤m ＜n.

证明:对于常系数线性方程(1)在变换(2)下化为常系数线性齐次方程组(3).

若方程组(3)的特征根λi为m 重根，则(A - λiE)m＝o(i ＝1，2，...，m，对于自然数m 满足2 ≤m ＜n)，并且对于常数列向量u1的m -1 个广义列向量ui(i ＝1，2，...，m) 满足:[13-14]

对于方程组(3)的齐次形式x′ ＝Ax，在(9)中，其线性无关的解，xi(m-1)＝um-1eλt、xim＝umeλt(i ＝1，2，…m，对于自然数m 满足2 ≤m ＜n)满足方程:

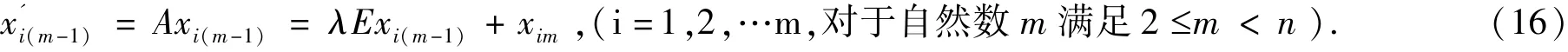
①对于(A - λiE)xim＝0(i ＝1，2，…m，对于自然数m 满足2 ≤m ＜n)，由定理3 将方程组(3)化为一阶线性微分方程形式

其中特征根λi的对应特征行向量为Ki(i ＝1，2，…m) .

②对于(A - λiE)xi(m-1)＝xim，( i ＝1，2，…m，对于自然数m 满足2 ≤m ＜n)，则

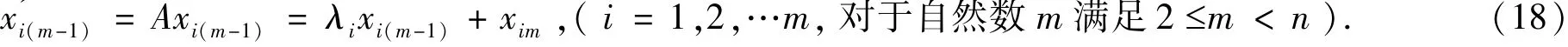
其中xim，( i ＝1，2，…m，对于自然数m 满足2 ≤m ＜n)为满足(17)的解.

由(A - λiE)m＝0 ，( i ＝1，2，…，m，对于自然数m 满足2 ≤m ＜n)，取对应线性无关的特征行向量为Km-1(对于自然数m 满足2 ≤m ＜n)，满足:

于是，有方程

其中i ＝1，2，…，m，对于自然数m 满足2 ≤m ＜n.

此时，由②中的关系式，得到

其中xim(i ＝1，2，…，m)为满足(17)的解.

即方程组(3)的化为以下形式

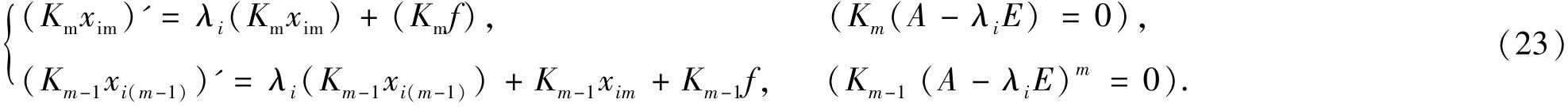
其中特征根λi对应特征行向量为Ki，xim、xi(m-1)为满足(23)的递推解，i ＝1，2，…，m，对于自然数m 满足2 ≤m ＜n.

显然方程组(23)可解的条件，是以下积分存在:

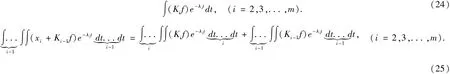
即方程(10)在可积条件(11)和(12)下可解.定理2 获得证明.

3 方程组解理论的应用

例1[2]解方程

解 由特征方程F(λ) ＝(λ ＋1)3＝0 ，得到特征根λ1＝λ2＝λ3＝-1 . 对于方程组

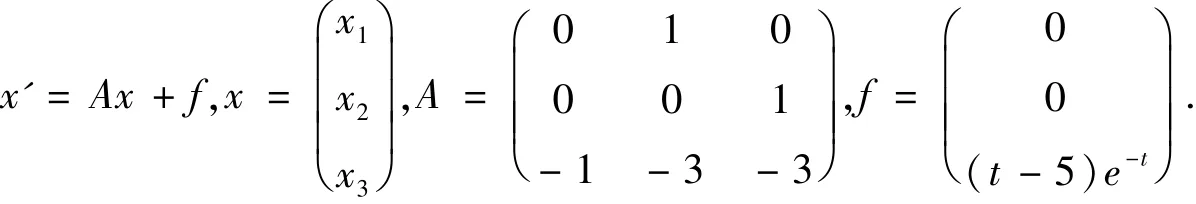
设λ1＝-1 所对应的特征行向量K1＝(k11，k12，k13) 满足

求得K1＝(1，2，1) ，由于

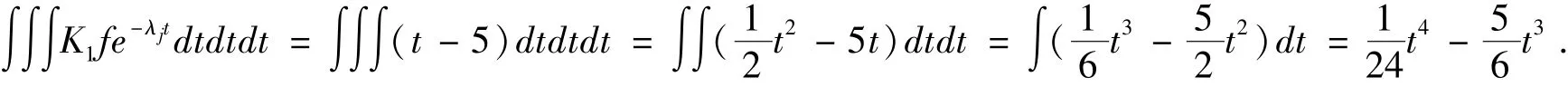
则有方程(x1＋2x2＋x3)' ＝K1Ax ＋K1f ＝- (x1＋2x2＋x3) ＋(t -5)e-t

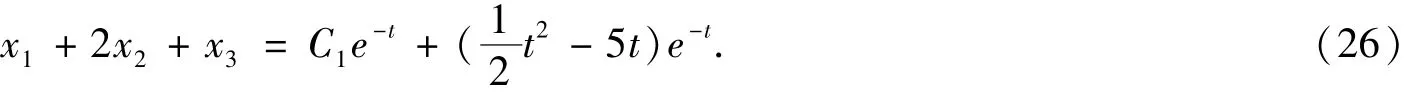
设λ2＝-1 所对应的特征行向量K2＝(k21，k22，k23) 满足

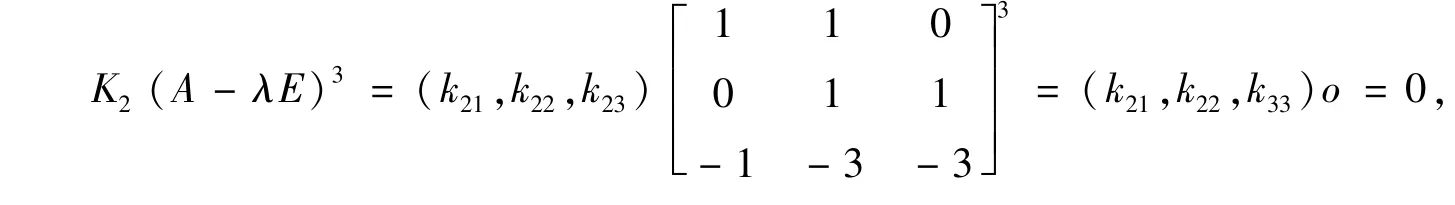
取K2＝(1，1，0) ，由于∫∫K2fe-λjtdtdt ＝∫0dt ＝0 ，则有方程

再取K3＝(1，0，0) ，由于∫∫K3fe-λjtdtdt ＝∫0dt ＝0 ，则有方程

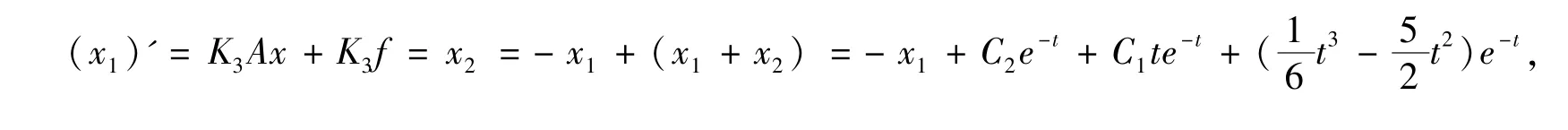
由式(28)，得到原方程的解

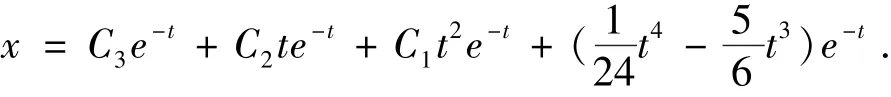
例2[8]解方程 x''＋9x ＝2cos3t ＋t.

解:由特征方程F(λ) ＝λ2＋9 ＝0 ，得特征根为λ1，2＝±3i.对于方程组

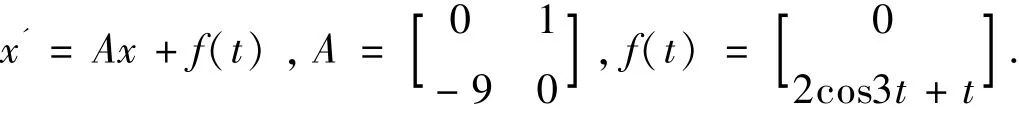
对于λ1＝-3i 所对应的特征行向量K1＝(k11，k12) 满足

求得K1＝(-3i，1) ，由于

则有方程

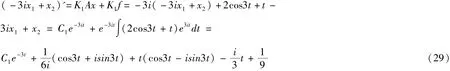
对于λ1＝3i 所对应的特征行向量K2＝(k21，k22) 满足

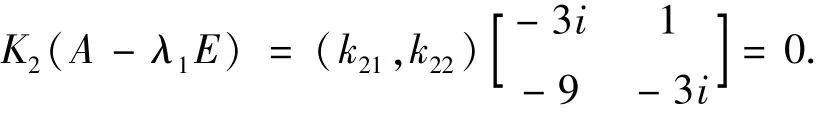
求得K2＝(3i，1) ，由于

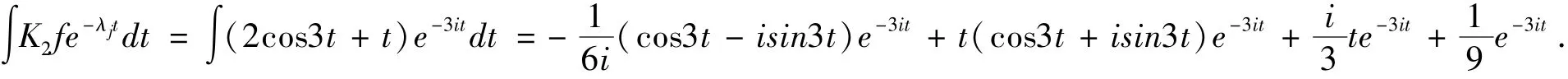
则有方程(3ix1＋x2)' ＝K2Ax ＋K2f ＝3i(3ix1＋x2) ＋2cos3t ＋t

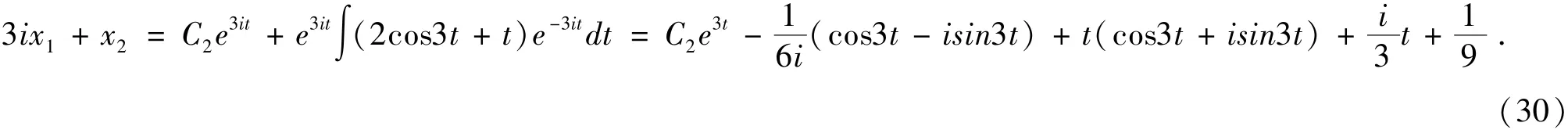
于是，由(29)和(30)得到方程组的解:

这种一次性求特解的方法，较原文由方程x''＋9x ＝2cos3t，x''＋9x ＝t，分别求特解的方法简便的多.

例3[1]解方程

解:由特征方程F(λ) ＝λ2-6λ ＋9 ＝(λ -3)2＝0 ，得特征根为λ1，2＝3 .对于方程组

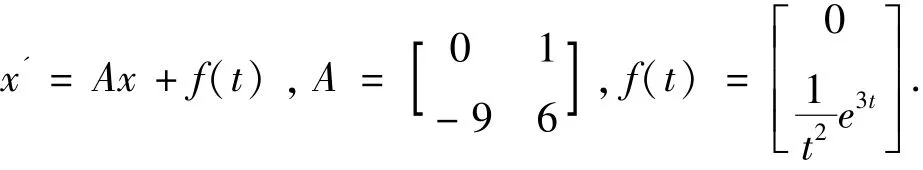
对于λ1＝3 所对应的特征行向量K1＝(k11，k12) 满足

设λ2＝3 所对应的特征行向量K2＝(k21，k22) 满足

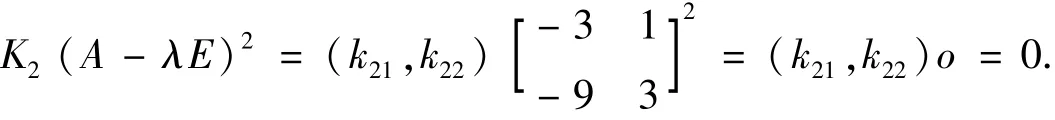
取K2＝(1，0) ，由于，则有方程

于是，(32)得到方程组的解:

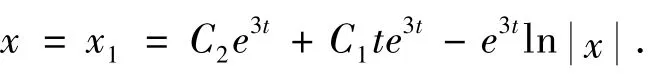
显然，本解法已将方程组(3)的函数f(t) 进行了扩展:f(t) ＝.但若取函数f(t) ＝，依然对于特征根λ ＝3 ，∫f(t)e-λjtdt ＝无初等积分形式，即对于函数f(t) ＝，

原方程是不可积的.

4 结论

对于线性常系数齐次方程L(x) ＝f(t) ，针对函数f(t) 满足可积条件的解法，扩大了文献[1-12]中往往注意讨论函数f(t) 的特殊形式:f(t) ＝pm(t)eαtcosβt ＋qn(t)eαtcosβt( pm(t)，qn(t) 分别为多项式)的解法，更具有意义；同时，在解法研究中，涉及到函数f(t) 不满足可积条件的线性常系数微分方程，对于研究这类“世界难题”的线性常系数微分方程，有一定启示.