适用于水电机组开机过程的轴承状态综合评估方法
2019-05-17罗红玲王卫玉郭定宇陈启卷
张 巍,罗红玲,王卫玉,郭定宇,陈启卷
(1.国网浙江省电力有限公司紧水滩水力发电厂,浙江 丽水 323000;2.水力机械过渡过程教育部重点实验室(武汉大学),武汉 430072)
0 引言
作为水电机组中的关键部件,轴系及轴承的运行状态对机组整体的稳定性具有重要影响[1]。水电机组具有开机时间短、并网速度快等特点,随着电网峰谷负荷的增大,机组的启停日趋频繁,这使得对轴系及轴承性能的要求越来越高,因此,对其状态进行评估十分必要[2-3]。
目前对于水电机组的轴系及轴承运行状态,一般是通过搜集稳定性试验数据或稳定运行工况下的运行监测数据[4],采用基于国标或行规的限值评估法和专家知识库来进行评估和预警。如文献[5]利用了时域和频域分析方法进行故障征兆提取,并结合专家知识和诊断规则实现对轴承状态的分析,但该方法需要通过离线方式获取数据,难以实现对轴承异常状态的实时报警,且过分依赖于专家经验。文献[6]首先通过支持向量机对特征值进行优化提取,然后将决策层的数据融合作为核心技术,构建了基于多传感器数据融合技术的轴承状态评估模型。但该模型较为复杂,目前不适合实际工程应用。文献[7]使用了模糊评判和相对劣化度模型来定量描述轴承状态。同样,相对劣化度与轴承状态间的对应关系单纯依靠专家经验和行业标准,受到的主观影响太强。
轴承故障属于机械因素故障范畴,如轴线对中不良、轴承间隙偏大或偏小、碰磨等。在稳定性试验中,主要是通过变转速试验来判别机组是否存在机械方面缺陷。由于水电机组的开机升转速过程与稳定性试验的变转速试验具有相似性[8],因此本文利用开机升转速过程的数据对轴承状态进行分析。轴承状态是一个多指标综合体,仅凭单项指标难以充分表征,需运用多项指标进行综合评价。但各指标间通常具有量纲不一致的特点,同时蕴含着复杂的非线性、动态关系[9-12]。因此,为实现在工程实际中对水电机组轴承状态进行综合评估,本文基于开机过程多项参数指标,建立了一个具有层次性的多指标轴承状态评估模型,利用主客观相结合的组合赋权法求取各项指标的综合权重,形成轴承状态的综合评估方法。
1 方法概述
1.1 轴承状态综合评估流程
在基于水电机组开机过程的轴承状态评估模型中,首先需要确定由参与评估的各项指标组成的因素集和由各评判等级组成的评判集,并利用概率论求出评判矩阵;然后分别通过改进层次分析法和熵权法求取因素集的主、客观权重,将两者相结合得到综合权重(即因素权向量);最后依据因素权向量与评判矩阵求出评判结果向量,对评判结果向量进行加权平均即可得到轴承状态的最终评估结果。轴承状态综合评估流程见图1。

图1 主客观权重相结合的轴承状态综合评估流程
综合评估方法的具体步骤如下:
(1)确定因素集和评判集
影响评估对象的n 个指标组成的集合称之为因素集U={u1,u2,…,un},其中ui代表影响评估对象的第i 个指标。有大量指标可用来评估水电机组轴系及轴承状态[13-14],综合考虑准确性和可操作性,这里选取主轴摆度、瓦温、油温3 个状态参量。
评估者对评估对象可能做出的m 种评估结果所组成的集合称为评估集实际上就是对轴承所处状态划分等级。依据国标和电站的运行规程,将机组的轴承运行状态各指标划分为4 个等级,评判集Q={优良、正常、异常、危险}。
具体的轴系及轴承状态综合评估结构如图2所示。
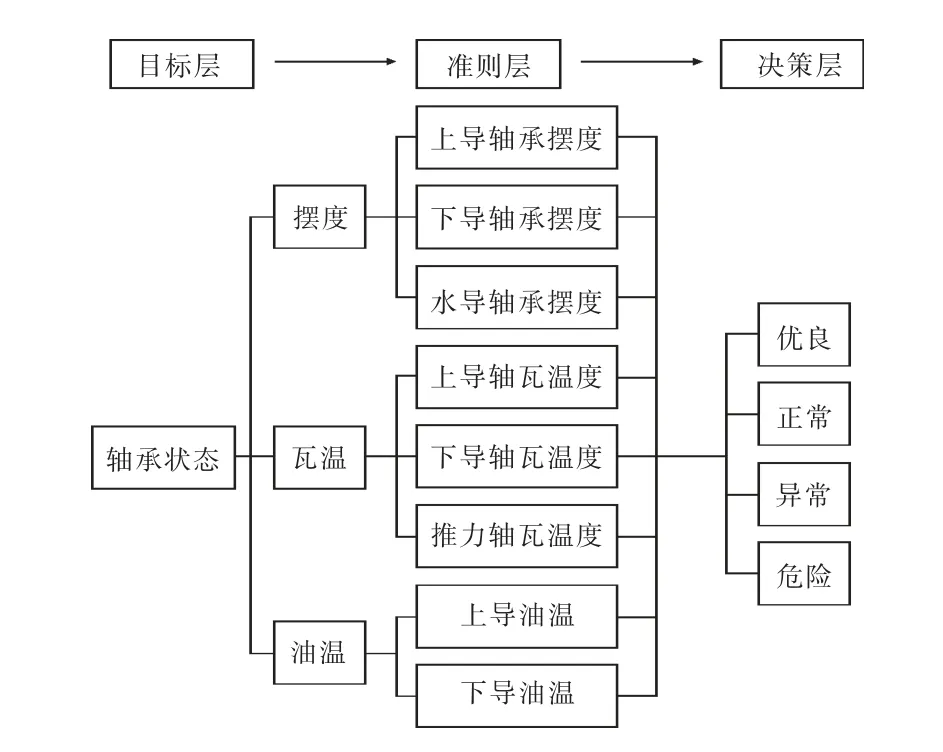
图2 轴系及轴承状态综合评估结构
(2)求取评判矩阵F
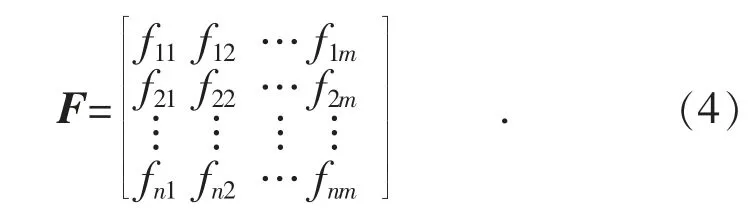
各指标具有不同程度的模糊性,因此需要对因素集U 中的每个指标做一个评估,从而可以得出因素集到评判集的一个模糊映射f[14],即:

式中:i=1,…,n;F(q)是Q 上的模糊集合全体,即评判矩阵F。
单项指标ui对评判集Q 中各评判指标的支持度为fij(j=1,…,m),fij间的差距越大,代表该指标在综合评估中起的作用就越大。如果某个指标对评判集Q 中各指标的支持度均相等,说明该指标的评判结果很分散,在综合评估中几乎没有作用。
确定评判矩阵的具体步骤如下:
①综合考虑规程、标准要求,将一次开机升转速过程的时间分为a 段,各单项指标分为m 个等级。
②判断在每一段时间内各指标处于何等级。
③统计指标ui在a 段时间中处于第j 级的次数Cij:

式中:cijk是指第i 个指标在第k 段时间内划分为第j 级的次数(cijk等于1 或0)。
④计算第i 个指标处于第j 个等级的概率:

将各项指标在各等级的概率分布依次形成n行m 列的评判矩阵F:
(3)计算各项指标的综合权重
在综合评估工作中,由于各项指标的重要程度不一,因此给各指标赋予适当的权重十分重要。利用组合赋权法求出轴承状态评估模型中各项指标的权系数A=[a1,a2,…,an]。
(4)计算各等级权系数
等级权系数B 由因素权向量乘以评判矩阵而得,如式(5)所示。

(5)求取最终评判结果
最后,轴承状态的最终综合评判结果R 是对B 进行加权平均求取,如式(6)所示。
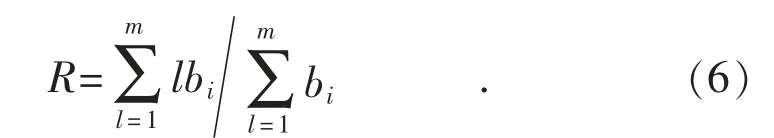
1.2 主客观结合的组合赋权法
目前,计算指标的权重主要分为主观和客观两种方法。主观赋权法属于定性分析,是基于评估者的主观经验来判断指标的重要程度,如层次分析法,其缺点是忽略了指标间的内在联系。客观赋权法是一种定量分析方法,其原理是通过一定的数学方法来计算权值,应用较为广泛的有主成分分析法、熵值法等,该方法虽能有效传递信息并区分各指标之间的差别,但仅用数据来说明问题可能会导致权重系数不合理的情况。因此,本文提出了考虑主客观权重的组合赋权法来求轴承状态综合评估模型中的各项指标的综合权重,既充分利用层次分析法的专家经验,又考虑到了权重的渐变性[15]。
1.2.1 基于改进层次分析法的主观权重计算
传统的AHP(层次分析法)需要做一致性检验来确定成对比较矩阵的不一致允许范围,若不通过检验,需要重新构造成对比较矩阵,这使得AHP 在实际应用中受阻。本文利用改进的AHP法可以构造出一组具有一致性的成对比较矩阵,可直接根据传递性获得各项指标的主观权重。构造方法如下:首先根据专家经验对n 个指标的重要度进行排序x1≥x2≥…≥xn,对xi与xi+1两个前后相邻的指标进行两两比较,这里引入标度值的概念用以定量描述两个指标之间的相对重要程度,记为ki。标度值大小如表1 所示[16]。

表1 标度值
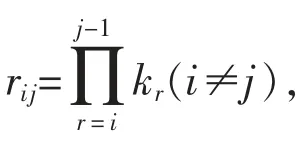
改进的AHP 法基于成对比较矩阵P 由式(8)计算可得到各项指标的主观权重:
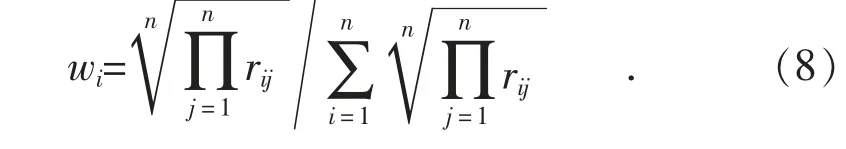

1.2.2 基于信息熵的客观权重计算

利用式(9)可以计算某单项指标ui的熵值hi:
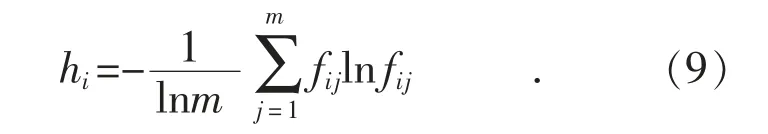
系统S 的熵值E 可由式(10)进行计算:

熵值越大则该指标对系统综合评估的影响越小,即客观权重值vi与hi成反比,指标ui的权重可用1-hi来度量。利用熵权法求得各指标的客观权重如式(11)所示:
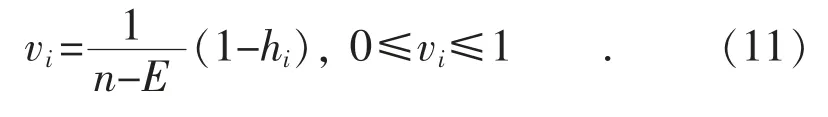
1.2.3 综合权重
某单项指标的综合权重ai可由式(12)确定:

各项指标的综合权重A=[a1,a2,…,an]。
2 案例分析
下面运用上述轴承状态综合评估方法对某电站的轴承状态进行综合评估。具体步骤如下:
(1)首先确定轴承状态的因素集U 和评判集Q。根据该电站的实际情况,U={水导摆度峰峰值、上导摆度峰峰值、下导摆度峰峰值、上导轴瓦温度、下导轴瓦温度、推力轴瓦温度、上导油温、下导油温}。依据国标和电站的运行规程,将机组的轴承运行状态各指标划分为4 个等级,评判集Q={优良、正常、异常、危险},即第1 级为优良,第2 级为正常,第3 级为异常,第4 级为危险。
(2)求评判矩阵F。对于机组振摆数值一类指标,目前国标还未建立特殊运行工况的轴系振动评估限制值,但国标GB/T 32584-2016《水力发电厂和蓄能泵站机组机械振动的评定》指出,由于在过渡过程中机组主轴摆度存在较大的随机分量,因此应较少地依赖瞬时振动值,而应更多地依赖有代表性的测量周期内测得的平均值。这里默认大修后一段时间内机组的轴承处于优良状态,因此若摆度峰峰值低于大修后一段时间内的统计平均值,则可以判定该项指标处于优良等级;优良与正常状态的划分以及正常与危险状态的划分由机组轴承间隙和国标中的规定共同确定:机组运行摆度(双幅值)的限值为0.7 倍轴承总间隙。同理,轴瓦温度和油温可依据DL/T 751-2014《水轮发电机运行规程》进行分级。表2 为评估该机组轴承状态的各指标分级。
现针对该电站的一次开机升转速过程进行分析,将该过程等分为14 个时间段,分别计算各项指标在每个时间段的值,并按表2 划分为对应等级,然后根据式(2)分别统计各项指标在整个升转速过程中处于各等级的时间,统计结果如表3 所示。利用式(3)求得各指标处于某一级的概率分布,如表4 所示。
根据表4 可以得到评判矩阵F:

(3)确定主观权重。具体步骤如下:
①根据专家经验(见表5)可知,3 个状态参量对轴承状态评价的重要程度:摆度峰峰值>瓦温>油温。具体到各项指标的重要程度:(水导摆度峰峰值=上导摆度峰峰值=下导摆度峰峰值)>(上导轴瓦温度=下导轴瓦温度=推力轴瓦温度)>(上导油温=下导油温)。

表2 轴承状态的各指标分级

表3 轴承状态各项指标处于各等级的统计结果

表4 轴承状态各项指标处于各级的概率分布
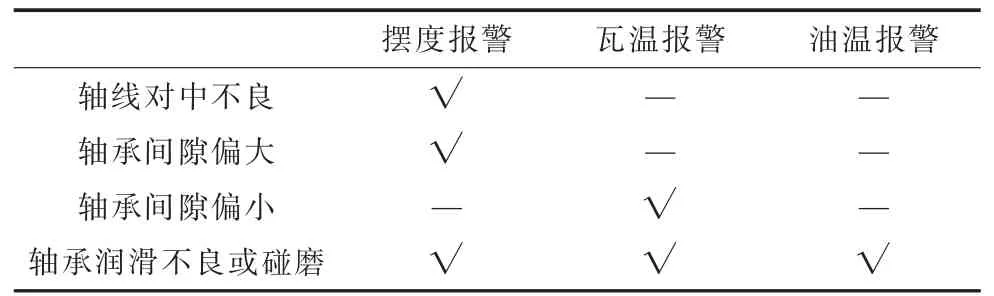
表5 基于专家经验的轴承故障特征
②通过对若干个专家调查后确定指标间的相对重要程度:k1=1,k2=1,k3=1.4,k4=1,k5=1,k6=1.2,k7=1。
③根据式(7)形成成对比较矩阵P。
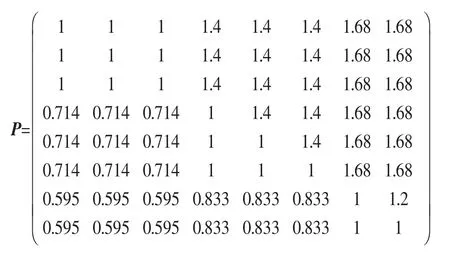
④利用式(8)计算出各单项指标的主观权重值:w1=0.150 7,w2=0.150 7,w3=0.150 7,w4=0.127 3,w5=0.122 1,w6=0.117 1,w7=0.091 7,w8=0.089 7。
(4)确定客观权重。具体步骤如下:
①利用评判矩阵F,根据式(9)求出每一项指标的熵值:h1=0.470 1,h2=0.431 7,h3=0.598 5,h4=0,h5=0,h6=0,h7=0,h8=0。
②根据式(10),求得整个系统的熵值:E=1.500 3。
③利用式(11)可以求得各项指标的客观权重:v1=0.081 5,v2=0.087 4,v3=0.061 8,v4=0.153 9,v5=0.153 9,v6=0.153 9,v7=0.153 9,v8=0.153 9。
(5)计算综合权重。根据式(12),计算得到因素权向量:
A=[0.103 1 0.055 3 0.026 1 0.041 1 0.031 6 0.025 2 0.016 9 0.014 5]
(6)计算评判结果向量。由式(5)得到各等级权系数:
B=AF=[0.189 4 0.122 6 0.001 90]
(7)计算综合评估结果。由式(6)经过加权计算得出综合评估结果:
R=1×0.189 4+2×0.122 6+3×0.001 9+4×0=1.403 1。
可见R 值介于上述划分的1~2 级之间,表明机组轴系状态介于优良和正常之间。
3 结语
本文建立了一个具有层次性的多指标轴承状态评估模型,通过概率论和模糊评判方法分析开机升转速过程的数据求出评判矩阵,随后利用主客观权重相结合的组合赋权法求出各项指标相应的权值,最后通过一个量化的数值来描述机组轴承状态。经实例验证,该方法适用于工程实际中机组轴承状态的综合评估。
