高速铁路槽形连续梁车-轨-桥相互作用动力分析

齐春雨

(中国铁路设计集团有限公司,天津 300251)

槽形梁能够降低线路纵断面，节省投资，其两侧腹板结构对车辆轮轨噪声的遮挡效应明显，降噪效果显著，尤其适合在铁路站场或城市市区使用，目前在城市轨道交通中应用广泛[1-7]。随着高速铁路路网密度的增大，高速铁路进入城区的概率增大，槽形梁基于其自身结构的优势，在高速铁路的应用日益增多[8-12]。在济青高铁设计中采用了(40+70+40+70) m 有砟轨道预应力混凝土槽形连续梁[13]。本桥为客货混跑，设计行车速度V≤200 km/h，建成之后，将成为国内外跨度最大的高速铁路双线预应力混凝土槽形连续梁。

目前，在TB10621—2014《高速铁路设计规范》中，仅对常用跨度双线简支箱梁不需进行动力检算的竖向自振频率限值做了规定，对于槽形连续梁这种新型结构类型桥梁，仍要求进行车桥动力分析[14]。另一方面，由于(40+70+40+70) m跨度为国内外较大跨度，在进行动力设计时，没有可供参考的案例。对此，本文以(40+70+40+70) m槽形连续梁为研究对象，分析其车轨桥耦合动力响应，以期为新型结构桥梁的动力学设计提供评判与参考。

1 槽形连续梁有限元模型与自振特性

槽形连续梁70 m跨跨中与支座处的截面如图1(a)和图1(b)所示，采用MIDAS Civil建立桥梁有限元模型如图1(c)所示。在有限元模型中，梁体和桥墩均采用空间梁单元模拟，其中梁体采用变截面梁单元，桥墩基础底等效刚度采用弹性支承弹簧模拟，支座的约束关系采用主从自由度来模拟，二期恒载等效转化为密度施加在梁体单元上，整个模型共包含156个节点、150个单元、35种截面，5个弹性支承弹簧、15个刚性约束。

图1 槽形连续梁有限元模型

槽形连续梁的自振特性如图2所示。由图2可知，槽形连续梁的一阶垂向阵型为主梁反对称竖向弯曲，二阶垂向阵型为主梁对称竖向弯曲，自振频率分别为1.564 Hz和2.463 Hz，槽形连续梁的横向振动特性与垂向自振特性相似，一阶横向与二阶横向的阵型分别为主梁的反对称和对称横向弯曲，对应的自振频率分别为4.130 Hz和4.223 Hz。

图2 槽形梁自振特性

2 铁路列车-轨道-桥梁耦合动力仿真软件

基于列车-轨道-桥梁动力相互作用原理，建立列车-轨道-桥梁/声屏障动力相互作用模型，并编制了铁路列车-轨道-桥梁耦合动力仿真软件RTTB。

该仿真软件主要采用Fortran语言进行编译，共包含6个模块，分别是：列车模块、轨道模块、桥梁模块、轮轨关系模块、桥轨关系模块和移动荷载列模块。软件通过输入铁路列车、轨道、桥梁数据及轨道不平顺数据，采用数值积分方法确定列车、轨道、桥梁系统各自由度的位移和速度，采用轮轨作用关系确定轮/轨之间的动态作用力，采用桥轨作用关系确定桥/轨之间的动态作用力，再根据列车、轨道、桥梁系统动力学方程求解各自由度的加速度，如此对时间步长循环即得到全部计算时间内整个车轨桥系统动力响应[15]。

软件具备对高速铁路、重载铁路、城际铁路的桥梁进行列车-轨道-桥梁耦合动力仿真分析的功能。利用高速铁路现场试验的测试结果，对软件的仿真结果进行了验证，结果表明，桥梁结构与轨道结构动力响应的测试结果与仿真结果基本吻合，测试结果和仿真结果在波形、幅值和变化规律上均保持较好的一致性，仿真软件RTTB能够较好地反映列车-轨道-桥梁动力相互作用特征，能够满足工程应用要求[16]。

3 济青高铁槽形连续梁振动模型、计算参数及工况

3.1 车-轨-桥相互作用模型

针对济青高铁槽形连续梁建立的列车-轨道-桥梁动力相互作用模型如图3所示。

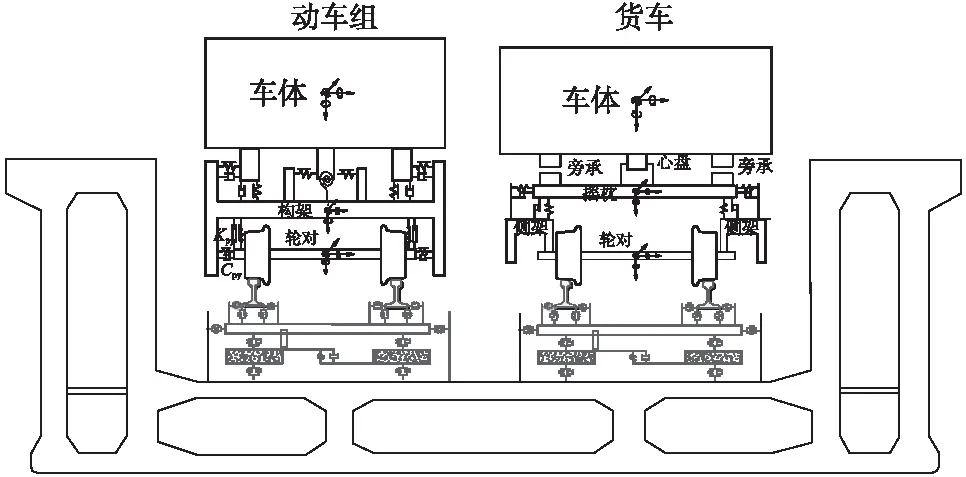
图3 车辆-轨道-槽形连续梁耦合振动模型

在模型中，动车组车辆模型采用35个自由度的四轴机车车辆模型，综合考虑车辆各悬挂装置，包括轴箱悬挂装置、空气弹簧或高圆簧、横向止挡、横向减振器、抗蛇行液压减振器、抗侧滚扭杆装置等[17]；货车模型采用具有47个自由度的三大件式货车模型，综合考虑各种非线性因素，包括轴箱间隙、轴箱与导框之间的摩擦、二系弹簧和摩擦楔块减振器，摇枕与楔块、楔块与侧架之间的摩擦、转向架的抗菱刚度与菱形角的关系等非线性环节[18]；轨道模型为有砟轨道模型，充分考虑钢轨、轨枕、道床的参振作用[19]；桥梁采用有限元方法建模[20]。

车辆与轨道的详细模型见相关文献[17-19]，桥梁的有限元模型如图1所示。

3.2 计算参数

针对桥梁设计条件，采用以下计算条件。轨道结构采用有砟轨道模型，轨道不平顺采用由德国低干扰谱生成的不平顺样本，波长范围2～120 m[21-22]。高速车分别采用CRH2和CRH3动车组模型，均为单编组列车，其中CRH2动车组采用T+M+M+T+T+M+M+T的编组模式(M为动车，T为拖车)，CRH3动车组采用M+T+M+T+T+M+T+M的编组模式。货车采用C64货车模型，假设货车为20辆编组。动车组的计算速度分别为120，140，160，180，200 km/h和220 km/h，货车的计算速度为40，50，60，70 km/h和80 km/h。

3.3 计算工况

由于红岛特大桥为客货共线桥梁，因此分别计算单列车过桥与双列车过桥时的动力响应，具体计算工况如下。

(1)CRH2动车组单列过桥与双列对开过桥。

(2)CRH3动车组单列过桥与双列对开过桥。

(3)货车单列过桥与对开过桥。

(4)CRH2动车组与货车同向并行过桥。

(5)CRH2动车组与货车双向对开过桥。

需要说明的是，在动车组与货车同时过桥时，货车的计算速度只包含60，70 km/h和80 km/h。

4 计算结果与分析

4.1 车辆动力响应与分析

不同工况条件下，车辆动力学指标最大值统计与评判结果如表1所示。在表1中，动车组统计动车与拖车动力响应的最大值，货车统计第1辆车与第2辆车动力响应最大值。由于动车组动车与拖车的静轴重不同，轮轴横向力的限值有所区别，从偏于安全考虑，轮轴横向力的限值依据静轴重取小值。

由表1可知，CRH2动车组与CRH3动车组在以≯220 km/h的速度单列或对开通过桥梁时，各项动力学指标均满足TB10621—2014《高速铁路设计规范》的要求，安全性指标均合格，并且有较大的余量，平稳性指标为优秀。C64货车在以≯80 km/h的速度单列或对开通过桥梁时，各项动车学指标均满足GB5599—85《铁道车辆动力学性能评定和鉴定规范》的要求，安全性指标均合格，并且有较大的余量，平稳性指标为优秀[23]。表1同时表明，动车组与货车对开或同向通过桥梁时，动车组与货车均行车安全，平稳性指标均为优秀。

表1 车辆动力学指标最大值统计和评判结果

4.2 桥梁动力响应与分析

由于双列对开时桥梁的动力响应要大于单列运行时桥梁的动力响应，在此仅给出不同工况条件下，槽形连续梁的动力响应最大值统计和评判结果，如表2所示。

表2 双列车运行条件下连续梁桥跨中动力响应最大值统计与评判结果

由表2可知，在本文的计算条件下，动车组双列对开、动车组与货车对开或同向运行时，桥梁的各项设计指标均满足规范要求，同时表明，动车组或者货车单列通过桥梁时，桥梁的各项设计指标也均满足规范要求，说明桥梁结构设计合理，满足设计要求。

由于TB10621—2014《高速铁路设计规范》中并未规定桥梁横向加速度的限值，表2中的桥梁横向加速度限值参考铁运函[2004]120号《铁路桥梁检定规范》的规定取为0.14g[24]。

在表2中，70 m跨与40 m跨的动力响应最值均为2跨70 m跨或2跨40 m跨的最值。同时，因为货车过桥的时间要远大于动车组过桥的时间，所以在进行动车组与货车对开或同向运行计算时，考虑了两列车在桥上交汇位置的影响，即在计算时，按照最不利交汇位置，设置了不同列车的上桥时间。

对比不同工况条件下桥梁动力响应的最值可知，动车组与货车对开或同向运行时桥梁跨中的位移最值要大于动车组对开或者货车对开时的位移最值。

5 结论

针对济青高铁(40+70+40+70) m槽形梁连续梁，建立了列车-轨道-槽形连续梁耦合振动模型，利用开发并经过试验验证的铁路列车-轨道-桥梁耦合动力仿真软件RTTB，计算了车轨桥相互作用系统的动力响应。在本文的计算条件下，得到如下结论。

(1)CRH2动车组与CRH3动车组在以≯220 km/h速度通过桥梁、C64货车在以≯80 km/h的速度通过桥梁、动车组与货车对开或同向通过桥梁时，车辆的安全性指标均合格，平稳性指标为优秀。

(2)CRH2动车组、CRH3动车组、C64货车在设计速度范围内以单列或者双列的形式通过桥梁时，桥梁的各项设计指标均满足规范要求，说明桥梁结构设计合理，满足设计要求。

(3)仿真软件RTTB能够较好地反映列车-轨道-桥梁动力相互作用特征，能够满足工程应用要求，通过针对济青高铁红岛特大桥进行动力仿真计算，验证了车辆-轨道-桥梁耦合动力仿真软件RTTB功能的可靠性。