第二代完整稳性衡准研究最新进展

王志荣， 周耀华， 户艳宏

(1.中国船级社， 北京 100007； 2.中国船级社 上海规范研究所， 上海 200135)

0 引 言

船舶稳性作为事关人命安全的重要性能指标，一直以来受到国际海事组织(IMO)的高度关注。在大量的事故统计资料和研究成果基础上，IMO制定了强制性的完整稳性和破损稳性法定要求[1-2]，但其中的完整稳性规则主要侧重于瘫船模式，并不涉及诸如参数横摇、纯稳性丧失、骑浪和过度加速度等波浪中的动稳性失效模式。随着包括集装箱船“APL CHINA”(C11)在内的若干实船事故的发生[3]，IMO有针对性地开展了第二代完整稳性衡准的制定工作。衡准包含参数横摇、纯稳性丧失、骑浪/横甩、瘫船稳性和过度加速度等5种稳性失效模式。目前，IMO基本完成了薄弱性衡准(第一层薄弱性衡准和第二层薄弱性衡准)的制定工作，并起草了稳性直接评估流程指南等衡准草案文本，相关技术文件形成了由5种失效模块、3层评估方法以及航行作业指南构成的第二代完整稳性衡准构架体系。

虽然第二代完整稳性衡准的制定工作已经取得了巨大进展，但尚存几方面的问题有待解决，包括参数横摇薄弱性衡准第二层运动预报方法的选取、薄弱性衡准的一致性验证、纯稳性衡准的一致性改进、用于稳性直接评估计算方法的精度验证指标研究等。对此，根据工信部批准的“第二代完整稳性衡准的应对和纯稳性丧失直接评估技术研究”项目，国内相关的设计和研究单位相继开展了船舶完整稳性5种失效模式的大量研究，包括大规模实船验证计算，研发具有独立知识产权的第二代完整稳性衡准评估软件，积极参与IMO第二代完整稳性衡准的制定等。相关成果以提案形式代表中国向IMO提交，其中SDC 4会议(2017)和SDC 5会议(2018)总计提交13份提案，极大地促进了新衡准的制定和完善工作，提高了中国在规则制定方面的发言权。

1 参数横摇Level2衡准运动预报方法选型

学术界及各国政府针对参数横摇Level 2衡准的运动预报方法以及实船敏感性预报开展了大量卓有成效的研究。截至2015年，IMO相关研究均基于采用平均法(Averaging Method, AVM)[4]开展，该方法通过求解单自由度非线性横摇方程获得参数横摇的稳态解。在2016年召开的IMO船舶设计建造分委会第三次会议(SDC 3)上，对于参数横摇Level 2衡准新增加了同样基于非线性力学方法的时域法(Time Domain Method, TDM)[5]作为备选方案。IMO希望通过发起新一轮衡准运动预报方法的选型研究，确保最终方案对于不同类型的实船均具有较好的工程适用性和预报精度。

1.1 基于求解稳态解的平均方法

该方法采用简化的横摇单自由度(1 Degree of Freedom, 1 DOF)方程开展参数横摇幅值的预报和敏感性分析。这种方法的主要思路是通过对不同船波相对位置下的波浪中初稳心高(TDM-GM， 量符号是hGM)和静水回复力臂(TDM-GZ， 量符号是LGZ)曲线进行拟合，模拟波浪中GZ曲线的周期性变化。其运动方程[2]为

(1)

(2)

式中：φ为横摇角；hGMmean为波浪中稳心高变化量的平均值；hGMamp为波浪中稳心高变化量的幅值；ωφ为横摇固有圆频率；ωe为遭遇频率；l2k+1为采用最小二乘法拟合静水中的GZ曲线得到的拟合系数，k为拟合阶数；α、γ分别为线性和三次横摇阻尼系数；t为时间。

1.2 求时域解的时域方法

该方法的主要思路是通过对不同船波相对位置下的波浪中初稳心高和波浪中静水回复力臂GZ曲线进行制表插值的方法，模拟波浪中GZ曲线/GM值的周期性变化。其运动方程为

sign(φ)ρgLGZ(t,|φ|)=0

(3)

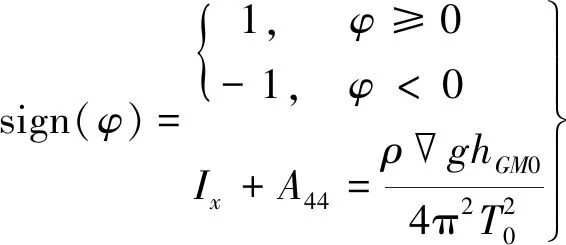
(4)

式中：Ix+A44为横摇惯性矩和附加惯性矩；为排水体积；ρ为海水密度；g为重力加速度；hGM0为静水中初稳心高；T0为横摇固有周期；δ1=2α，δ3=γ为阻尼因数，可采用简化Ikeda方法计算；LGZ(t,|φ|)为波浪中LGZ值，即船与入射波处于时刻t的相对位置，波浪中对应横摇角φ的GZ曲线取值。

1.3 研究进展

由于备选的时域方法的若干重要计算参数的设置尚未确定，有必要通过验证获得适当的取值，确保计算结果的稳定性。采用两艘集装箱船(S25、C11)和一艘车辆滚装船(S10)的模型试验数据，验证、对比两种备选方法的预报精度，分析各方法精度差异的原因，最后针对中国不同类型的大量实船装载工况及事故船进行敏感性水平预报，通过对比分析平均法和时域法的敏感性计算结果，为Level 2衡准参数横摇运动预报方法的选型给出若干建议。

表1和图1为样船主尺度和试验船模照片。图2和图3为部分精度验证结果[6]。基于模型试验的精度验证，进一步开展两种数值模拟方法的实船敏感性预报结果对比。图4为基于38艘各类型实船的衡准敏感性校核计算结果对比。通过以上研究，验证AVM和TDM的计算精度及其对实船敏感性预报的影响。对于IMO参数横摇Level 2衡准，建议选取AVM和TDM作为运动预报方法。试验对比验证和实船敏感性计算表明两者均能给出趋势相似、偏于保守的预报结果，且敏感性预报结果差异较小。当采用AVM和TDM时，标准值可维持现有值不变。相关研究成果已作为技术提案提交IMO讨论[7]。

表1 船舶主尺度(实船尺度)

图1 S25船模示例

图2 S25船和S10船迎浪参数横摇幅值[6]

图3 C11船迎浪参数横摇幅值

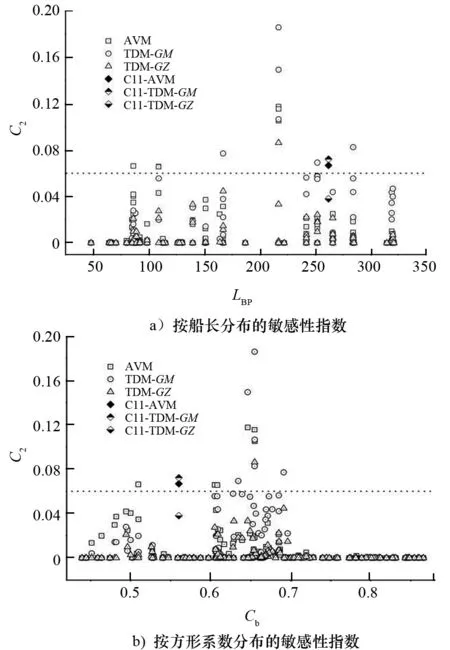
图4 38艘各类型实船衡准敏感性指数C2

2 参数横摇和纯稳性丧失薄弱性衡准一致性检验

根据IMO对第二代完整稳性衡准的基本构架体系，3层评估方法的计算复杂性依次递增，评估准确性也依次提高。只有在第一层薄弱性衡准没有通过的情况下，才进行第二层薄弱性衡准的评估；在无法通过第二层薄弱性衡准时，进行第三层评估——稳性直接评估；在3层衡准评估都无法通过时，必须对船型进行重新设计或制定航行操作指南，以避免稳性失效的发生。对于薄弱性衡准而言，早期研究阶段曾出现过满足第一层衡准的要求却无法满足第二层衡准要求的情况，即产生了所谓的一致性问题。IMO于SDC 3会议上决定在2016年度开展衡准样船计算，进一步检验衡准样船结果的一致性。国内根据IMO的工作计划，针对中国大量实船开展了校核计算，结合中国普通商业运营船舶对5种失效模式的敏感性，着重针对中国船舶开展参数横摇、纯稳性丧失和过度加速度薄弱性衡准的一致性检验。

2.1 参数横摇衡准

参数横摇是在纵向大幅波浪(迎浪或随浪)中，由复原力臂曲线周期性变化导致的一种参数激励共振现象。

第一层薄弱性衡准是通过经验公式判断船舶在等效规则波中初稳心高的变化幅度来确定敏感性，经验公式为

(5)

第二层薄弱性衡准是基于概率方法，对航行在北大西洋海域的船舶，计算其发生参数横摇的概率，分第一次校核和第二次校核两部分。第一次校核是对第一层薄弱性衡准的扩展，第二次校核是采用单自由度非线性横摇运动方程计算等效规则波下的参数横摇幅值，并进行不规则波中的敏感性指数加权计算，得到最终的敏感性指数C2。第二次校核包括AVM和(TDM-GM、TDM-GZ)两种，参见第1.1节和第1.2节。

2.2 纯稳性丧失

纯稳性丧失是由随浪航行时船舶复原力臂减小而导致的稳性失效模式。此衡准的核心是判断波浪中船舶GZ曲线的稳性特征，计算入射波条件规定的等效入射波与船舶处于规定的若干位置时的GZ曲线，通过判断GZ曲线的若干特征计算敏感性指数，并依据海况发生概率进行加权计算，得到最终的敏感性指数[8]。

入射波直接采用国际船级社协会推荐的不规则波散布图[9]中的272个海况，换算为波长与船长比为1.0的等效规则波，对每个海况进行敏感性指数加权计算，由波浪中稳性特征判断[10]。

(6)

式中：φv为稳性消失角与进水角的较小值，取入射波与船舶11个相对位置对应的波浪中GZ曲线中该角度最小值；RPL1=30°为标准值。

(7)

式中：φs为等效波中10个位置对应GZ曲线与力臂值RPL3平衡角度的最大值；RPL2对客船为15°，对其他船舶为25°。

最终，衡准校核加权得到敏感性指数最大值max(CR1,CR2)。

2.3 过度加速度

过度加速度是船舶横摇等运动导致横向加速度过大的现象，主要对货物造成损坏，严重时造成人员伤害。

第一层薄弱性衡准是采用简单的经验公式，以固有周期的共振横摇估算最大加速度值。

第二层薄弱性衡准是通过频域求解单自由度线性横摇运动方程[11]，根据计算出的横摇响应算子计算不规则波中的加速度响应，再进行敏感性指数加权计算，得到敏感性指数C。

(8)

θ=θaei ωet

(9)

MFK=(a+bi)·ei ωet

(10)

2.4 国内研究进展

在工信部二代稳性项目实施中，采用了两种方式开展一致性检验，包括假定装载工况的矩阵计算和经批准的实际装载工况校核计算。假定装载工况矩阵是根据批准的实际装载工况吃水和hGM范围组合假定而成的，矩阵中常有不同数量的工况在实际运营中不会出现。因此，该矩阵计算仅具备一定的参考意义，更适合于开展许用GM曲线的计算。经批准的实际装载工况是指满足目前生效的2008国际完整稳性规则的要求，经主管机关批准可用于安全运营的实际工况。矩阵计算样船采用4艘集装箱船、1艘滚装船、2艘LNG船、2艘海洋供应船(Offshore Support Vessels, OSV)、2艘救助船和3艘客船，总计14艘样船。经批准的实际装载工况校核计算采用11艘实船，包括1艘集装箱船、1艘LPG船、1艘打捞起重船、1艘沥青运输船、1艘滚装船、3艘OSV和3艘海洋调查船。样船和实船主尺度如表2所示。图5给出了部分样船矩阵计算结果,横坐标为不同计算工况的吃水和hGM值，纵坐标为根据不同衡准方法计算得到的敏感性结果与标准值的差值。通过以上研究得到了这3种失效模式的一致性检验结果。研究表明对于中国样船而言，一致性问题主要集中于纯稳性丧失衡准。据此，确立了中国对于一致性问题的基本立场[12-13]，为后续开展薄弱性衡准改进研究确立了研究方向。

表2 矩阵计算样船与实际装载工况计算样船尺度

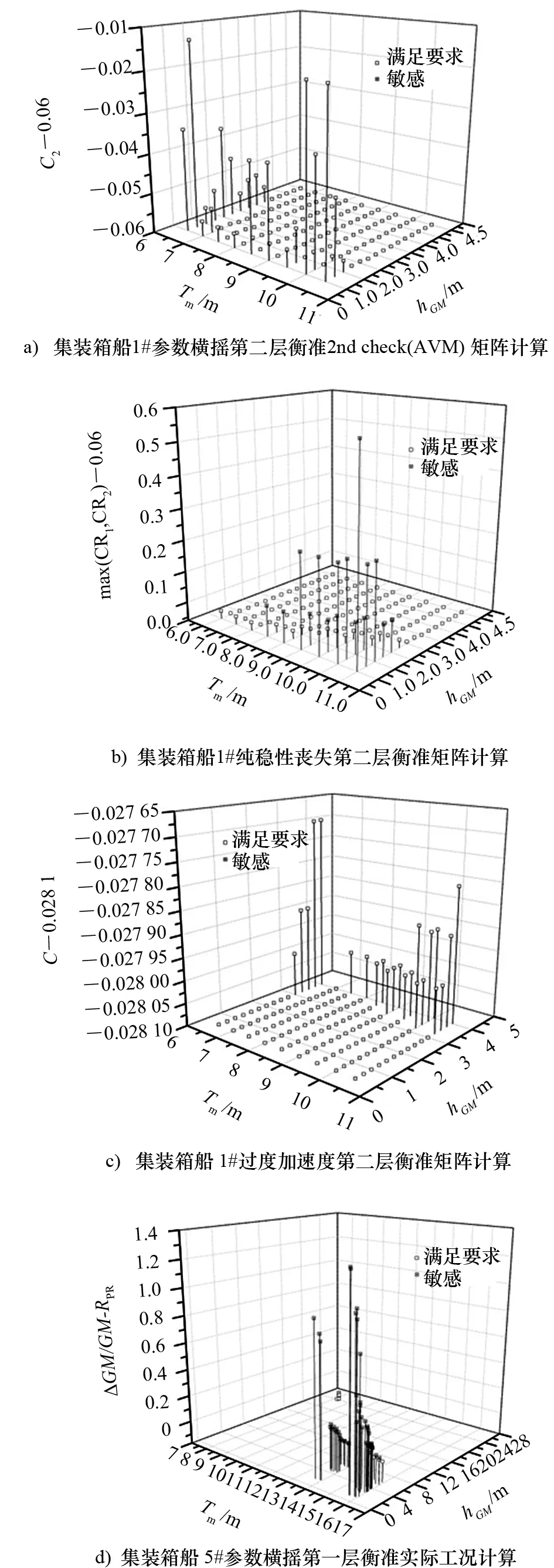
图5 部分矩阵和实际工况计算结果

3 纯稳性薄弱性衡准的一致性改进

3.1 SDC4会议改进建议

针对纯稳性丧失衡准通过样船计算结果表现出来的一致性问题，IMO在SDC 4会议上对解决方案进行了讨论。提高第一层衡准的入射波条件，将入射波陡由现有的0.03提高至0.05。通过提高第一层衡准保守程度的方式改善一致性。根据这一提议，开展了11艘典型实船的对比计算，如表3所示。由对比计算结果可见，3艘OSV和2艘海洋调查船仍然存在一致性问题，这表明SDC 4会议考虑的改进措施实质上对于OSV和海洋调查船型改善效果不明显。

表3 算例数对比结果统计

3.2 国内针对一致性改进的方案

由于验证表明SDC 4会议的改进建议均未能有效地改善一致性，因此有必要进一步研究全新的改进措施。分析既往纯稳性丧失样船计算结果发现，一致性问题可能由两个方面的原因所导致：(1)由于现有第一层衡准的等效波陡取为固定值，对于中小尺度船舶，等效入射波所表征的海况将会降低；(2)第二层衡准中增加了校核船舶抵御横倾力矩RPL3能力的要求(即对GZ曲线的特征隐含了要求)，而第一层衡准仅校核波浪中最小初稳心高，后者无法完全反应船舶波浪中GZ曲线的特征。据此，提出针对薄弱性衡准的改进建议：首先，改进入射波陡假定的合理性，对于第一层衡准的入射波陡系数Sw，可改为采用有义波高Hs=7.5 m、平均跨零周期Tz=6.5～18.5 s计算得到的等效波陡中的最大值；其次由于现有的最小hGM值衡准实际无法完全反映波浪中GZ曲线特性，因此无法完全反映船舶抵御横倾力矩RPL3的能力。有鉴于此，提议对于第一层衡准，新增对于RPL2对应波浪中LGZ值的判断。

采用修改方案后，不同尺度船舶的校核海况得到了统一。针对所提出的纯稳性丧失第一层衡准的改进建议，开展样船对比计算验证其有效性。计算样船包括11艘实船。图6给出了第一层判定敏感的装载工况比例，以及存在一致性问题的装载工况比例。

结果表明：采用新提议的方法后，小尺度船舶第一层判定敏感的装载工况比例有所增加。所有装载工况的第一、二层衡准校核结果均维持一致，一致性问题得到了显著改善。相关结果已提交IMO工作组讨论[14]。

3.3 用于稳性直接评估计算方法的精度验证指标

自SDC 4次会议起，直接计算衡准流程指南的制定被列为本议题工作最高优先级，以美国在SDC 1会议提议文本为基础，完成了指南草稿文本的起草工作，以待进一步讨论和修改。该指南的编制思路是针对5种失效模式分别给出数值软件必须考虑的运动自由度和受力、环境条件设定以及数值模型精度的定性和定量要求。其中，最为核心的是针对数值模型精度的定性和定量研究。针对参数横摇、纯稳性丧失、过度加速度和骑浪/横甩失效模式的稳性直接评估数值模型进行样船计算研究，通过与模型试验精度的对比分析，针对计算精度的定性和定量要求提出对应的建议[15-18]，用于进一步制定衡准流程指南草案。

图6 改进方案有效性比较

例如，针对参数横摇稳性直接评估，采用3艘样船的模型试验结果用于进一步的验证研究，包括2艘集装箱船(10 000TEU和4 250TEU)和1艘滚装船。分析混合方法的数值模拟精度和局限性。还分析混合方法的潜在缺陷，其中部分缺陷已通过采用全非线性计算流体力学(CFD)方法开展对比研究得到初步验证。根据收集到的经验，提出针对直接计算衡准流程指南草案定性精度指标的若干建议。部分船模的照片和数值模拟计算结果如图7～图9所示。指南草案主要针对横摇幅值提出预报精度要求，因此，主要对数值预报获得的横摇幅值与模型试验结果进行对比。在10 000TEU集装箱船计算的19个算例中，15个满足指南草案对于横摇幅值的精度要求，即当横摇幅值小于静水GZ曲线最大值横倾角时，误差应小于10%横摇幅值。

图7 4 250TEU集装箱船的参数横摇现象

图8 10 000TEU集装箱船参数横摇幅值预报结果

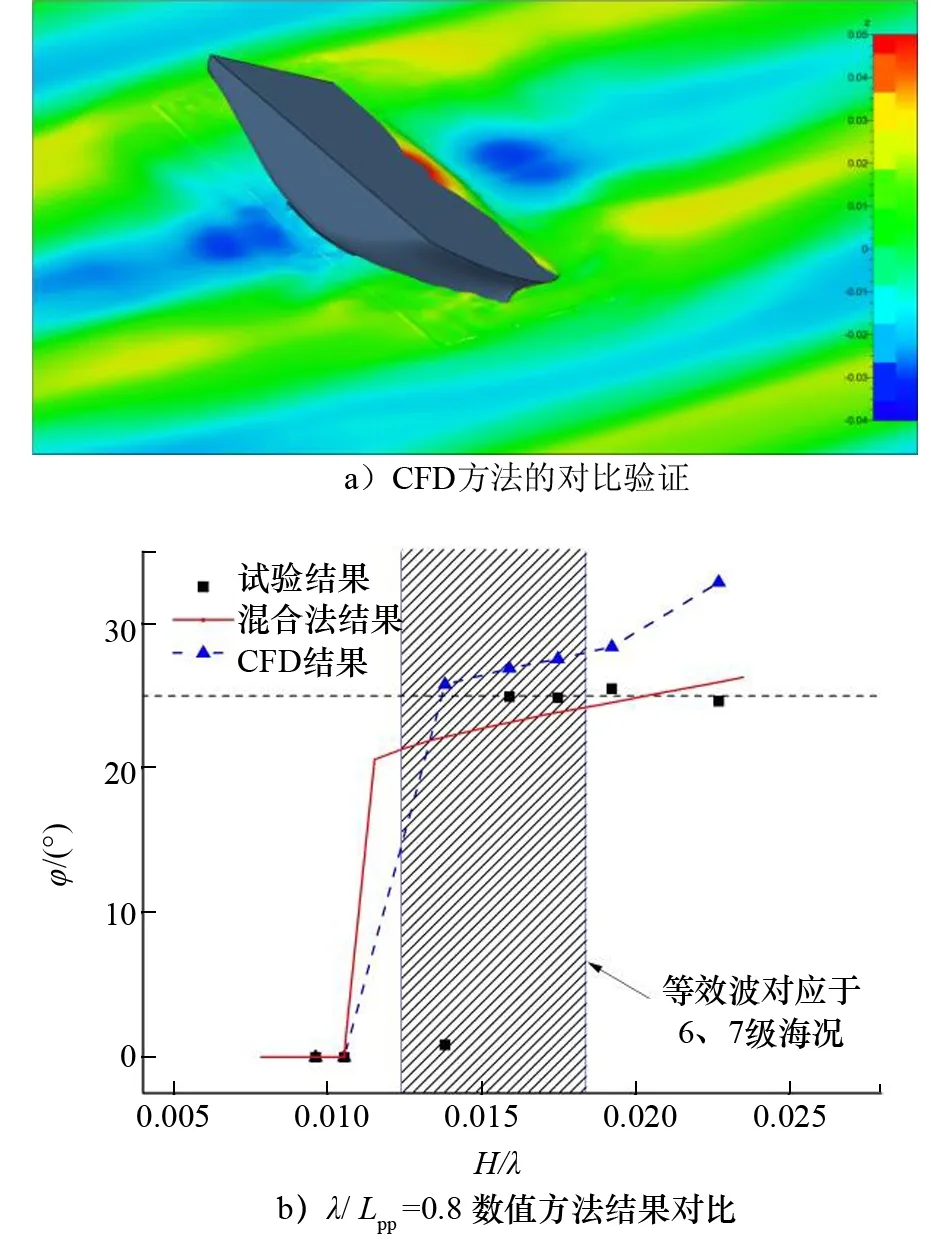
图9 基于CFD方法的数值方法横向比较 (10 000TEU集装箱船)

4 结 语

在最近两届的SDC会议上，中国代表团以样船计算和模型试验等为技术支撑，针对第二代完整稳性衡准开展了大量基础性研究工作，主要涉及参数横摇Level 2衡准运动预报方法的选型研究、参数横摇和纯稳性丧失薄弱性衡准一致性检验研究、纯稳性薄弱性衡准的一致性改进研究和用于稳性直接评估计算方法的精度验证指标研究等方面。根据上述研究成果，总计提交了9份提案文件和4份信息文件，对于薄弱性衡准的改进和稳性直接评估指南的制定向IMO提出了大量建议。

根据IMO对第二代稳性研究的工作计划和取得的进展，结合中国在船舶第二代稳性研究方面所取得的成果和技术水平，建议将以下几方面作为未来工作的重点研究方向：

(1) 通过扩大样船计算，进一步检验薄弱性衡准的一致性，积累对第二代稳性衡准敏感性水平的船型数据。

(2) 继续研究纯稳性丧失薄弱性衡准的适用条件。

(3) 继续针对纯稳性丧失薄弱性衡准的一致性问题开展研究。

(4) 开展更多的关于参数横摇、过度加速度和纯稳性丧失稳性直接评估方法的实船计算和试验对比验证研究，积累使用经验。

(5) 加强针对实船操作指南/操作限制指南制定方面的研究，结合实船商业运营的经验，制定相关指南文件。