基于均衡适应度的云工作流调度算法

方 军 张 璋 张雪峰 杜 聪 马 涛 刘 鑫

1(国家质量监督检验检疫总局信息中心 北京 100088)2(北京中质信维科技有限公司 北京 100088)3(北京赛迪工业和信息化工程监理中心有限公司 北京 100048)4(石家庄铁道大学信息学院 河北 石家庄 050043)

0 引 言

云计算环境中，资源可根据应用需求动态地分配至用户任务，而用户对资源的付费方式是即付即用的，这极大地区别于传统的分布式计算环境[1]。这种特有的使用特征使得云计算提供了对科学工作流调度的最好支持[2]。每一种大规模的工作流应用均可建模为有向无循环图结构，结构中包含有大量相互依赖或相互独立的任务，有些可同步调度执行，而有些则需要按照严格的先后次序调度执行。为了满足用户对于应用任务执行的不同QoS需求，云环境中的工作流调度需要寻找有效可行的调度方案，实现工作流任务与多资源间的映射与执行。

云环境中任务调度的主要目标是如何为每个任务选择合适资源，并决定任务在资源上的执行序列，同时满足用户给定的QoS需求[3]。已有工作流调度系统多优化调度效率忽略了优化代价。由于云服务使用的有偿性，优化调度代价将具有更加重要的意义。同时，云资源使用具有自身特点：资源在用户间共享与竞争并存，资源可用性具有变化性，资源异构且即付即用等。基于以上考虑，必须研究新的工作流调度算法以适应云资源使用的特性及满足用户方的多需求性。

1 相关研究

任务调度问题重点关注于任务与资源间的映射及执行管理，通常，该问题是NP难问题。因此，在多项式时间内寻找其最优解理论上是不可能的。当前有关任务调度算法的研究可总结出以下几种类型：1) 代价最优，截止期限约束。文献[4]提出动态代价有效截止时间约束启发式调度算法，实现公有云的单一工作流调度。文献[5]提出一种代价最优化算法，利用任务复制机制增加满足应用截止期限的概率。除了以上启发式算法，文献[6-7]则利用搜索算法和元启发式算法优化了相同目标。2) 时间最优，预算约束。工作流的预算定义为用户执行任务向资源方支付的最大费用。文献[8-10]提出了启发式算法最小化执行时间，同时需要满足预算约束。文献[11]提出安全与预算感知工作流调度算法，可在满足安全级别的同时降低总执行时间。3) 时间最优，代价最优。部分工作尝试在最小化时间和代价两种QoS参数间取得均衡。文献[12]提出关键路径优先算法CPF，利用工作流的扩展与压缩机制优化时间和代价。文献[13]提出满足Pareto最优的代价-时间最优调度算法。同样地，利用Pareto最优的概念，文献[14]通过设置反映用户对于时间和代价偏好的代价有效因子，提出执行时间和代价最小化调度算法。然而，以上研究是考虑一个QoS为约束而优化另一个QoS，或者同时优化代价和时间，不同于以上研究，本文将同时考虑时间和代价的约束，并同时对两种QoS进行优化。

结合已有研究，提出一种工作流任务遗传调度算法，利用遗传操作实现执行时间与代价同步优化。

2 问题描述

2.1 问题定义

本文所讨论的具有网络拓扑的任务调度问题可定义为分配应用中的任务至处理器集合的问题，同时以最小化总执行时间为目标。因此，任务调度输入包括一个任务图和处理器图，输出为一个调度方案，代表每个应用任务节点与处理器间的映射关系。先给出本文中应用的符号说明，如表1所示。

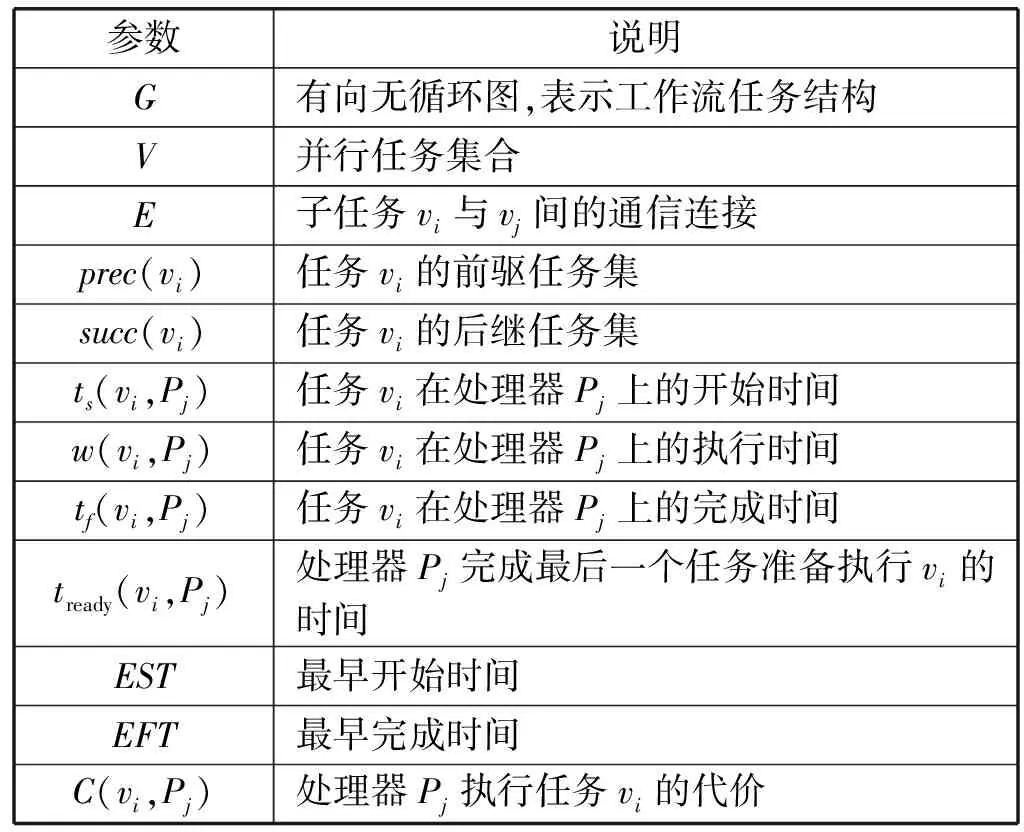
表1 符号说明

定义1以有向无循环图DAG表示一个任务图G=(V,E,w,c)，如图1所示，顶点集V={v1,v2,…,vk}表示并行子任务集合，有向边集eij=(vi,vj)∈E描述子任务vi与vj间的通信关系，w(vi)表示任务vi的计算时间，c(eij)表示对应传输数据d(eij)所需要的任务vi与vj间的通信时间。若任务vi不存在任一前驱，则Pred(vi)=0，称为一个入口任务ventry。若不存在任一后继，则succ(vi)=0，称为一个终止任务vend。任务由负载wli组成，定义了任务在计算资源上处理的工作量。任务也可由前驱子任务集prec(vi)和后继子任务集succ(vi)构成，ts(vi,Pj)表示任务vi在处理器资源Pj上的开始时间，w(vi,Pj)表示执行时间。因此，任务的完成时间为tf(vi,Pj)=ts(vi,Pj)+w(vi,Pj)。

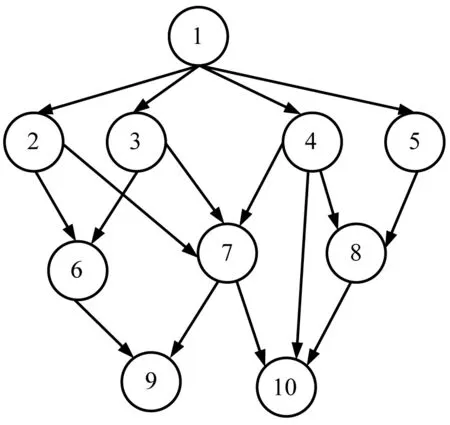
图1 DAG任务图示例

假设任务执行环境满足以下条件：

条件1：任务不能开始执行，直到其所有输入已经汇聚为止。每个任务仅出现在一个调度中。

条件2：就绪时间tready(vi,Pj)表示处理器Pj完成其最后一个分配任务准备执行任务vi的时间。因此，

(1)

式中:exec(j)表示执行于处理器Pj上的任务集，tf(ezi)=tf(vz)+c(ezi)，prec(vi)表示vi的前驱任务集。

条件3：令[tA,tB]∈[0,∞]表示处理器Pj上无任务执行的空闲时间间隔。任务vi∈V可在[tA,tB]内被调度至Pj，若满足：

max{tA,tready(vi,Pj)}+w(vi,Pj)≤tB

(2)

定义2处理器图TG=(N,D)表示描述处理器相互网络关联的结构图，如图2所示。模型中，N为有限顶点集，有向边dij∈D表示顶点Pi至顶点Pj间的有向边，Pi,Pj∈N。每个处理器Pi可控制其与其他处理器间的处理速率pi和链路带宽bwi。

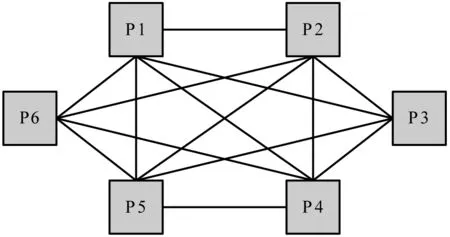
图2 处理器图

2.2 基于遗传的任务调度算法设计

给定任务图G=(V,E,w,c)和具有网络拓扑的处理器图TG=(N,D)，算法目标是选择最佳调度方案执行任务，本文选择遗传算法对任务调度进行优化，命名算法为CTAGA算法。

遗传算法的一般步骤如图3所示，它是受自然物种进化启发的一种强大的解空间搜索方法。相比其他算法仅能找到局部最优解，遗传算法GA可以利用过去搜索到的最优解去扩展新的解空间搜索区域。算法中，一个可行解即为一个个体，即染色体，本文中所考虑的将任务分配至可用的处理器集中即为染色体中的一个基因。算法可以维持一个随机产生个体的种群进化多代，种群中个体的质量由适应度函数进行评估，具有较高适应度值的个体代表质量较好的调度解。基于适应度，父代被选择产生子代，即通过交叉、变异操作，产生新的染色体种群，这样可以改进染色体质量。最终，新的种群将逐渐收敛至最优解。以下具体描述算法的实现细节。

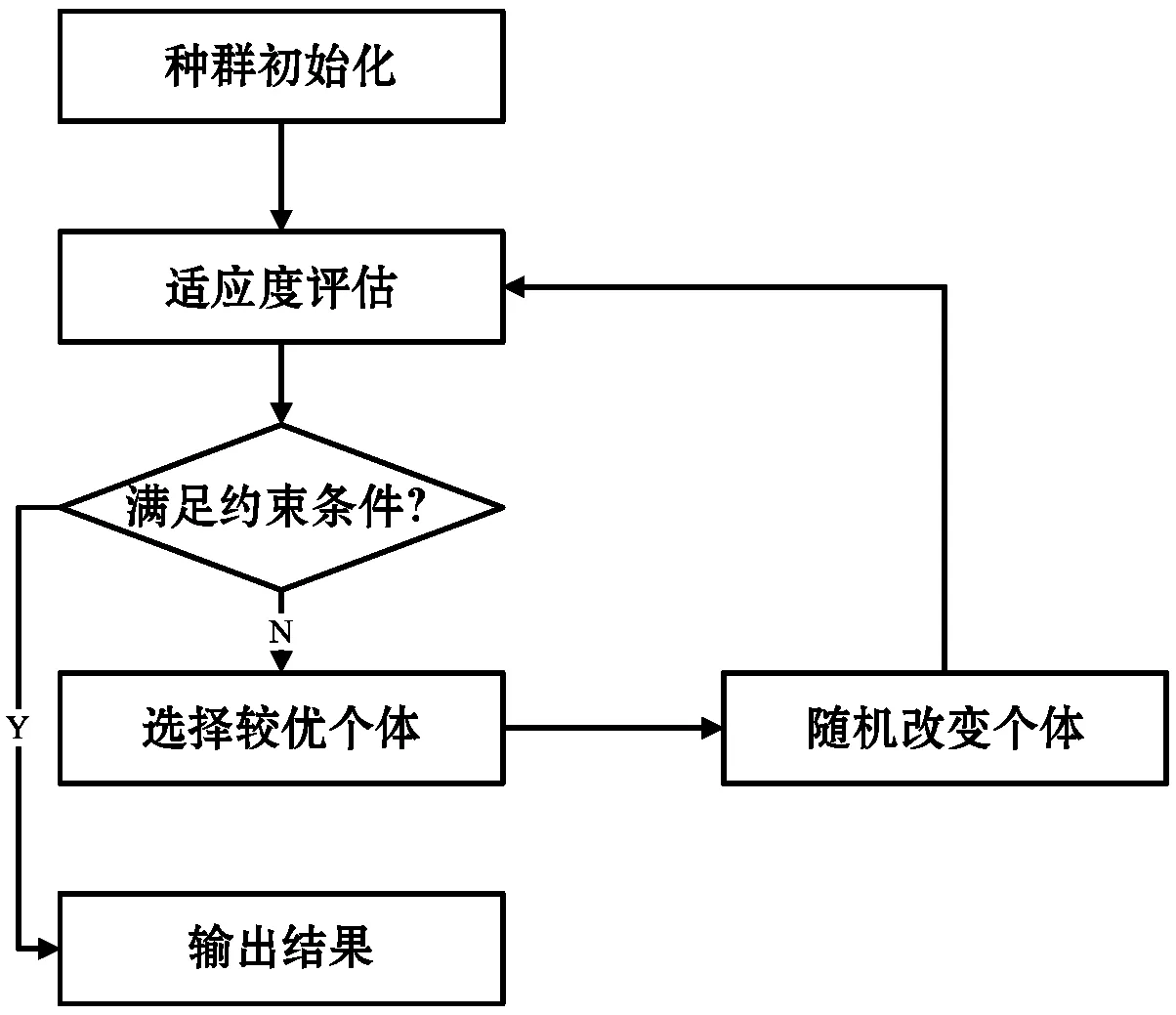
图3 遗传步骤

1) 个体表示 选择种群的一个个体(见图4)描述调度问题的一个可行解，个体包含任务分配的排列。每个分配由一个任务和相应的分配处理器组成。每个个体中任务的最早开始时间和最早完成时间，可以改变其后继任务的相关时间。而这种改变可能导致遗传算法更加复杂的状态。

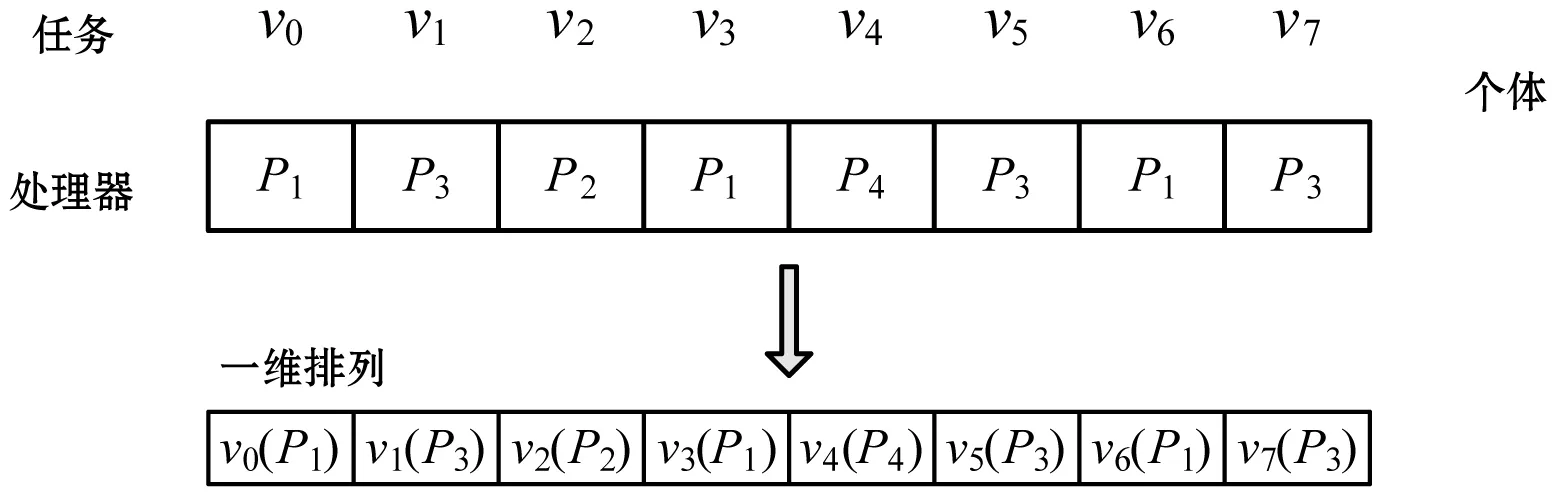
图4 一维排列表示的个体

可见，一维排列不适合于表示工作流任务，由于它仅定义了哪个处理器被分配至每个任务，而无法显示任务分配至每个处理器的顺序。然而，执行顺序对于工作流应用是必需考虑的。本文使用一种二维排列表示一个调度方案，如图5所示。在二维排列中可以显示每个处理器上的任务序列。在遗传操作过程中，二维排列可转化为一维排列。

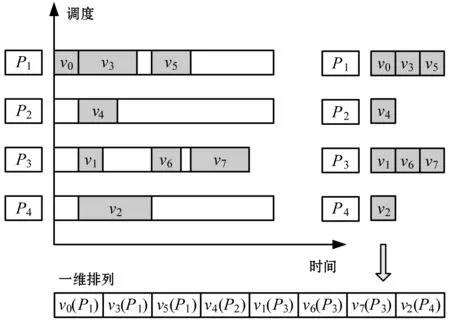
图5 二维排列

2) 种群初始化 初始化种群通过随机启发式方法产生的个体集合组成。每个个体由任务与分配的处理器的配对构成。

3) 适应度函数 适应度函数用于量化种群中每个个体的优劣。根据适应度值，父个体被选择产生子代。由于算法目标是最小化调度长度，同时考虑网络连接与用户代价，适应度函数则需要取决于EFT和用户支付代价。以下阐述EFT和任务在处理器上的执行代价问题。

任务的开始时间定义为其最后一个前驱任务的完成时间。因此，为了决定开始时间，需要搜索满足条件2和条件3时处理器Pj上的最早空闲时间间隔[tA,tB]。任务vi在处理器Pj上的开始时间ts设置为：

(3)

因此，任务vi在处理器Pj上的最早开始时间计算为：

(4)

(5)

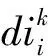
EFT(vi,Pj)=w(vi,Pj)+EST(vi,Pj)

(6)

另外，算法同时考虑用户执行任务时的需要支付的代价。任务vi在处理器Pj上的执行代价定义为：

(7)

式(7)中的代价定义如下：

处理代价为：

(8)

式中：c1为处理器Pj以处理速率pj执行工作流时单位时间的代价。

令tmin为并行任务中第一个完成任务的完成时间，c2为单位时间任务的等待代价，ti为任务vi的完成时间，则等待时间代价为：

(9)

令c3为从处理器Pj传输数据时单位时间的代价，则通信时间代价为：

(10)

令c4为单位数据的存储代价，sti为任务vi在处理器Pj上的存储数据量，则存储代价为：

(11)

进一步，可计算任务vi使用处理器Pj的内存代价为：

(12)

式中：smem为利用的内存大小；c5为单位数据的内存代价。

基于以上代价，可以建立同步考虑计算代价与EFT间的均衡适应度函数U(vi,Pj)：

(13)

通过联立考虑cost(vi,Pj)和EFT(vi,Pj)的适应度函数，可以决定种群中哪个个体是最适合满足适应度的个体，即应计算其最小值。

4) 遗传操作

(1) 选择。根据种群个体适应度选择新的个体。个体选择为父代的概率正比于适应度值。均衡值越小的个体越优秀。

(2) 交叉。个体的交叉操目标是从当前种群中随机选择两个个体(父个体)进行遗传交叉以产生新的个体，从而在子代中获得更好的个体。算法引入三种交叉方法：单点交叉、两点交叉(或多点交叉)和均匀交叉。交叉概率设置为在区间[0.6,1]。具体示例分别如图6、图7和图8所示。

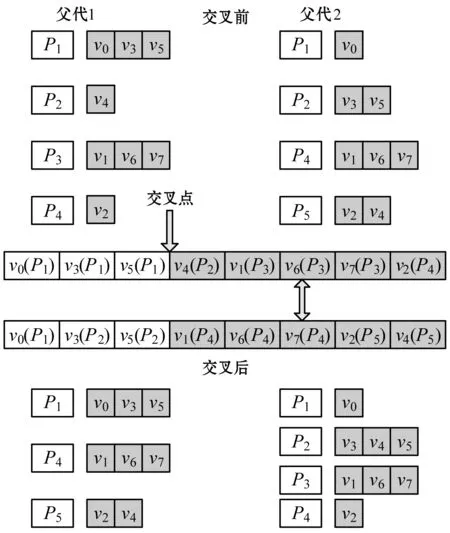
图6 单点交叉

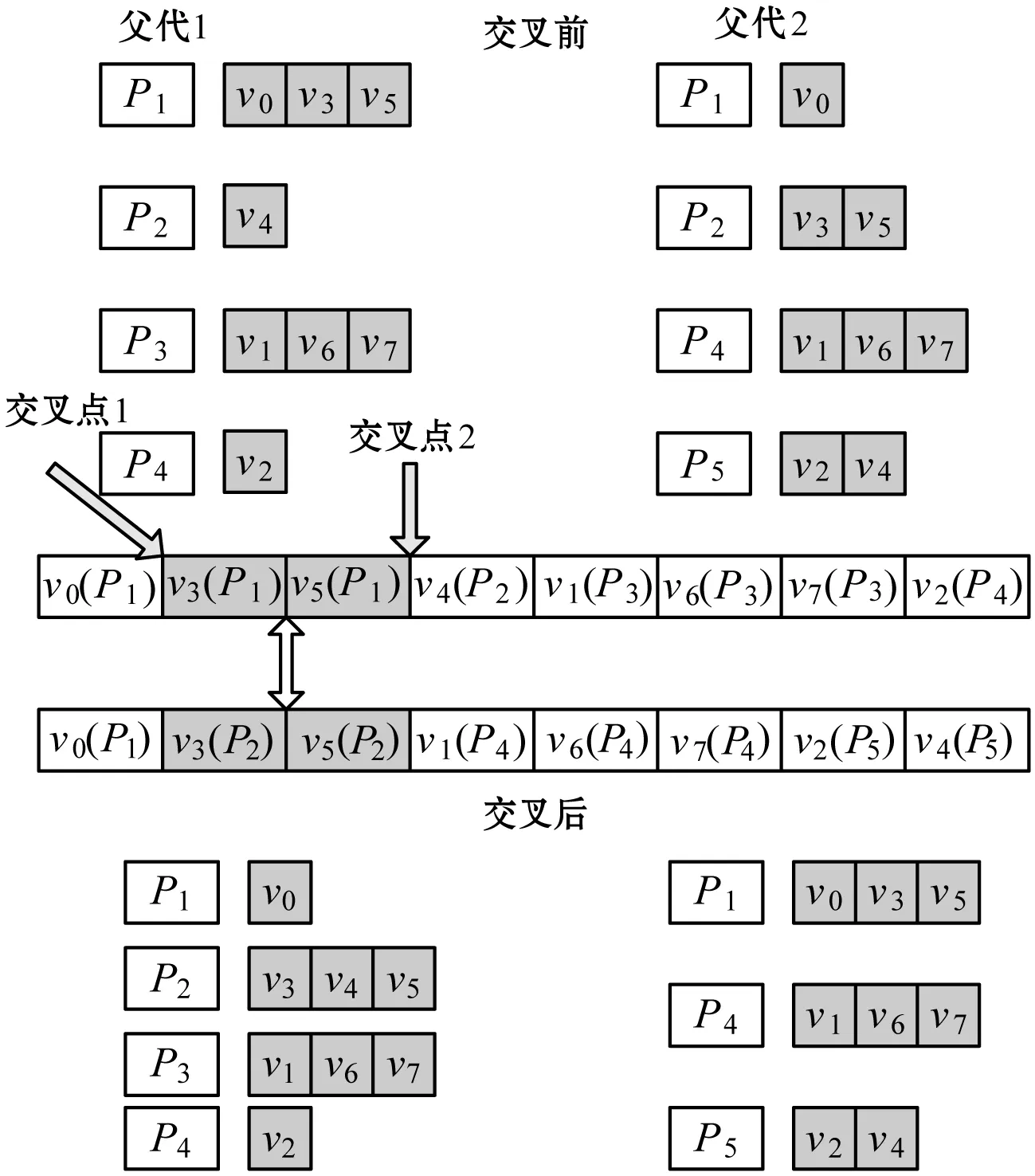
图7 两点交叉

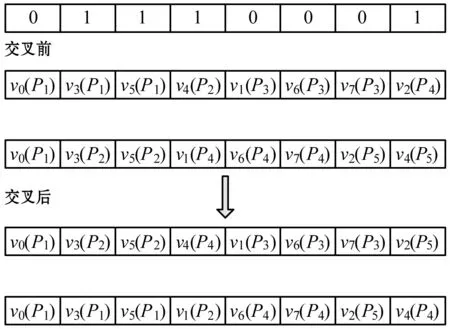
图8 均匀交叉

交叉操作将由以下步骤决定：

① 从父个体中随机选择一个、两个(或多个)交叉点；

② 以上随机点将每个个体划分为左右两部分；

③ 交叉互换两个个体的左右两个部分；

④ 通过联立父个体的两个部分得到新的子代个体。

单点交叉中(图6)，在个体中随机选择一个位置。第一个子个体即为联立第一个父个体的左边部分和第二个父个体的右边部分得到的，第二个子个体即为联立第二个父个体的左边部分和第一个父个体的右边部分得到的。两点交叉中，需要随机选择个体中的两个位置，如图7所示。两点交叉的好处在于可以避免单点交叉的固有问题，即确定染色体的头部基因和尾部基因总是分裂的。均匀交叉中，先随机产生一个二进制序列(图8)，该序列决定哪些比特从父个体中进行复制。比特值表示每个个体中元素的位置，比特密度决定个体如何交叉。遗传算法在实现过程中将根据种群大小各取三分之一的种群分别进行三种交叉操作。

(3) 变异。遗传算法中，变异操作可以从当前种群中的单个个体上产生新的子代，变异可以通过搜索新的更佳的基因维持个体的多样性，以避免问题解陷入局部最优。算法引入两种变异操作：交换变异和替换变异。遗传算法在实现过程中将根据种群大小各取交叉后的一半种群分别进行两种变异操作。

交换变异的目标是在个体上重新分配处理器至一个随机任务。所选处理器为随机选择，且具有执行该任务的能力。图9(a)描述了一种交换变异情形，其中，分配至任务v4的处理器P2交换为处理器P4。相比而言，互换变异则是在相同时槽内改变一个个体中相同处理器上独立任务的执行次序。图9(b)是一种互换变异情形，任务v0和v5进行了互换变异。

图9 变异操作

本文设计了几种任务调度算法进行性能比较，这些算法均是最小化工作流调度长度或调度代价为目标的。算法1为贪婪优化算法GCA，算法将每个工作流任务分配至执行代价最小的处理器上。算法2为内容感知调度算法CASA，算法通过网络连接状况建立了一个基于最早完成时间的调度表，并依该表进行任务调度。算法3即为本文所设计的同步考虑网络连接内容与代价的调度算法CTAGA，算法可以实现在执行时间与代价间均衡的调度，并得到全局最优解。三种算法的伪代码如下所示：

算法1GCA伪代码

1Input:G=(V,E,w,c),TG=(N,D)

2Output: A new task scheduling

3FunctionGCA(G,TG)

4 Sort taskvn∈Vinto list L according to priority

5Forvn∈V

6 Find the best processorPjwhich minimize the execution cost of taskvn

7 AssignvnonPj

8Returna new task scheduling

算法2CASA伪代码

1Input:G=(V,E,w,c),TG=(N,D)

2Output: A new task scheduling

3FunctionCASA(G,TG)

4 Sort taskvn∈Vinto listLaccording to priority

5Forvn∈V

6 Find the best processorPjwhich allow EFT ofvn,taking account of network bandwidth usage

7 AssignvnonPj

8Returna new task scheduling

算法3CTAGA伪代码

1Input:G=(V,E,w,c),TG=(N,D)

2Output: A new task scheduling

3FunctionCTAGA(G,TG)

4 Generate initial population

5 Compute fitness of each individual according to Fitness Function

6Repeat//New generation

7Forpopulation_size

8 Select two parent from old generation

9 Recombine fitness for two offspring

10Insert offspring in new generation

11Untilpopulation has converged

3 实验分析

3.1 实验配置

本节通过数值仿真评估算法性能，实验参数如表2所示。利用CloudSim及JDK-7u7-i586 JAVA环境进行实验，通过CloudSim可以构建模拟云基础设施和服务模型。仿真中利用Million Instructions per Second MIPS描述处理器的处理能力。

表2 参数配置

3.2 实验结果

图10-图11是本文算法与对比算法的性能比较情况。图10表明GCA算法得到了最差性能，CASA在调度长度上性能最优，而本文算法处于中间，优于GCA算法20%左右。然而，在图11中的代价方面，尽管CASA拥有最佳的性能，但它却拥有最高的代价。CTAGA在调度长度与代价方面起到了很好的均衡，通过与CASA比较，CTAGA能够为用户节省约20%的代价；与GCA比较，CTAGA则能节省约25%的调度时间。表3是三种算法在不同任务数量的情况下得到的均衡适应度的值的情况。虽然本文算法CTAGA在三种算法中无法同步实现调度长度和调度代价的最优，但其得到的均衡适应度值是三种算法中最小的，这表明算法选择的个体在调度时间和代价的综合性能上是最优的。

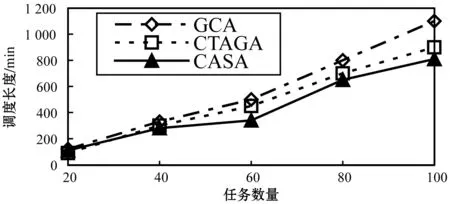
图10 调度长度比较

图11 代价比较

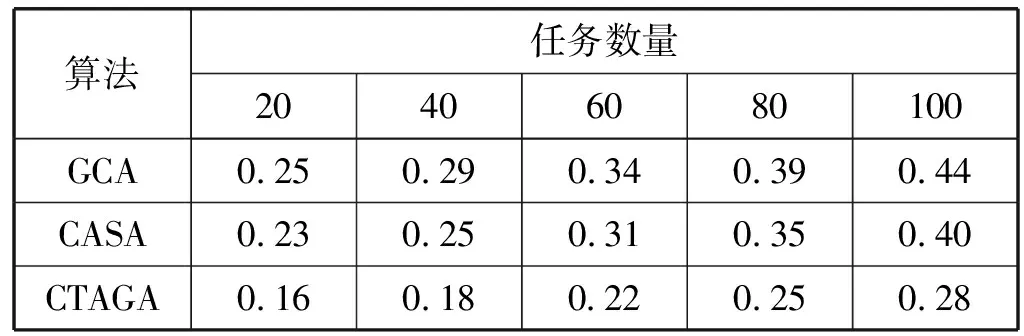
算法任务数量20406080100GCA0.250.290.340.390.44CASA0.230.250.310.350.40CTAGA0.160.180.220.250.28

实验还观察了处理器数量和迭代次数对CTAGA算法得到的代价和调度长度的影响，结果如图12和图13所示。结果表明，处理器数量越多，系统性能越好，但是代价也越高。当遗传代数逐步增加时，工作流调度长度会随着代价的降低而降低，这是由于每个所选个体需要同步考虑代价和执行时间因素导致的。

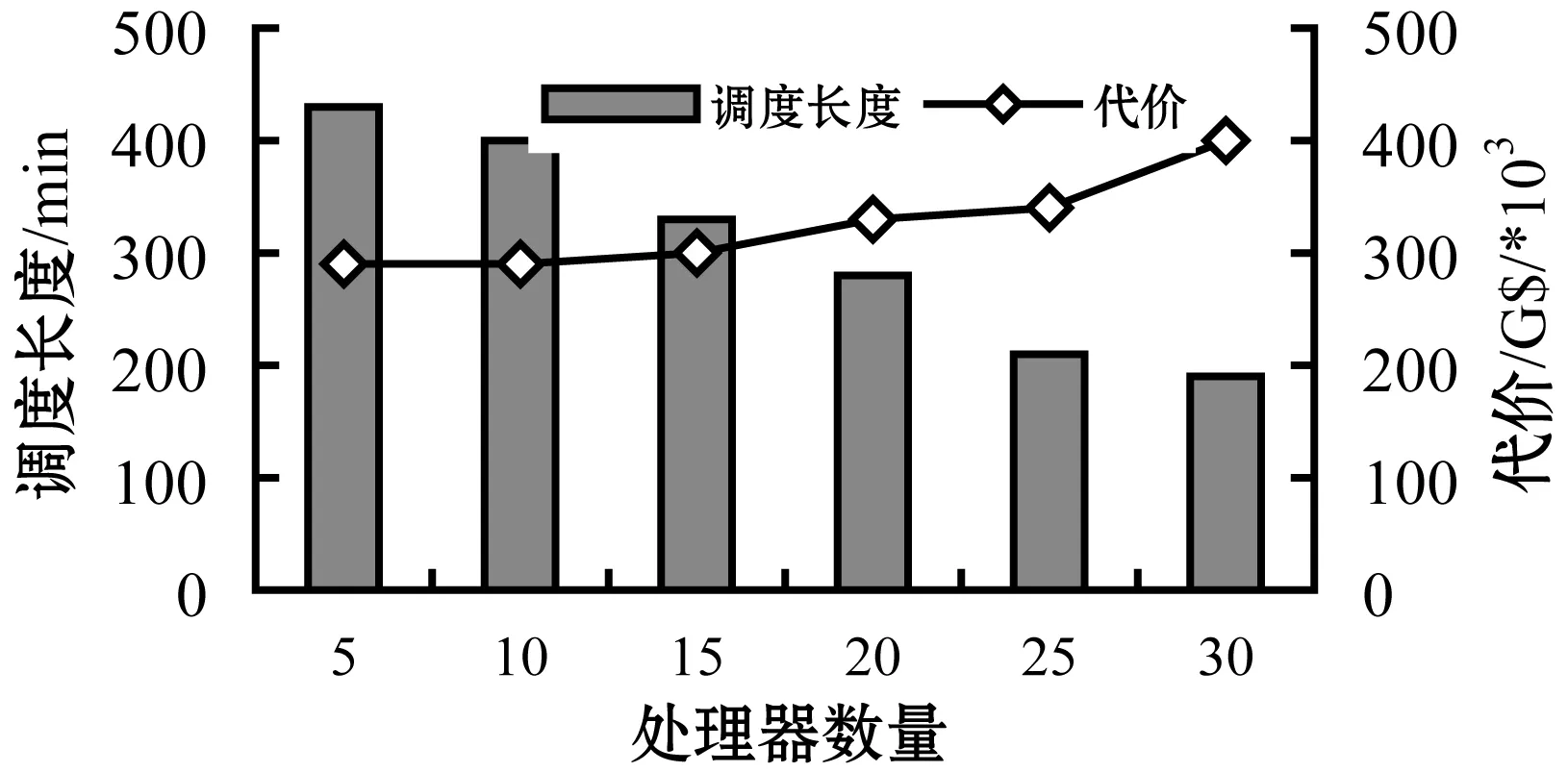
图12 处理器数量对调度长度和代价的影响

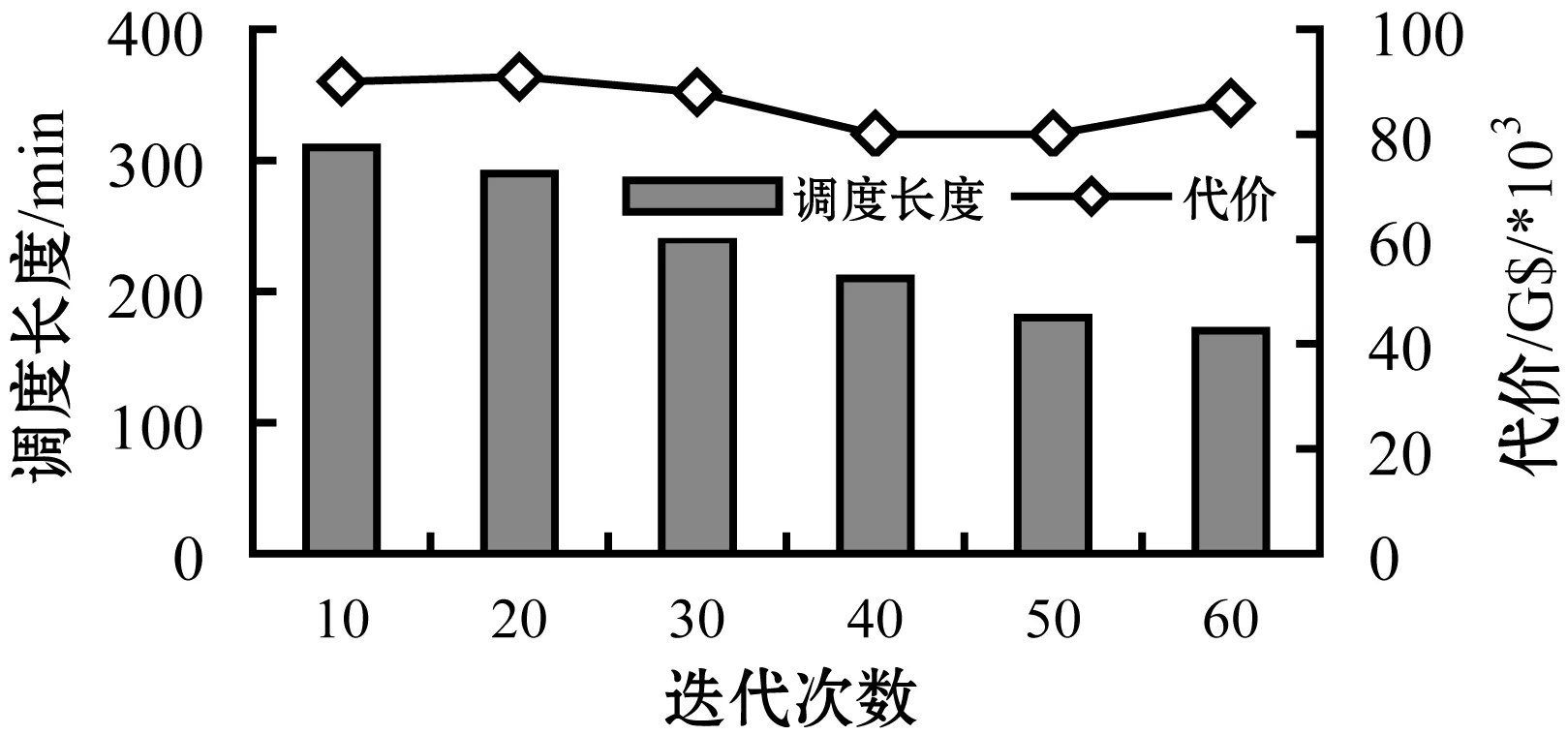
图13 迭代次数对调度长度和代价的影响

最后，实验还观察了CTAGA算法在不同个体数量下的性能情况。如图14所示，当个体数量从30变为90时，可以看到种群规模的增加并没有极大影响执行代价，而找到最快解的概率则在变高。另一方面，调度时间在78 min后的50 min里展现出下降趋势。

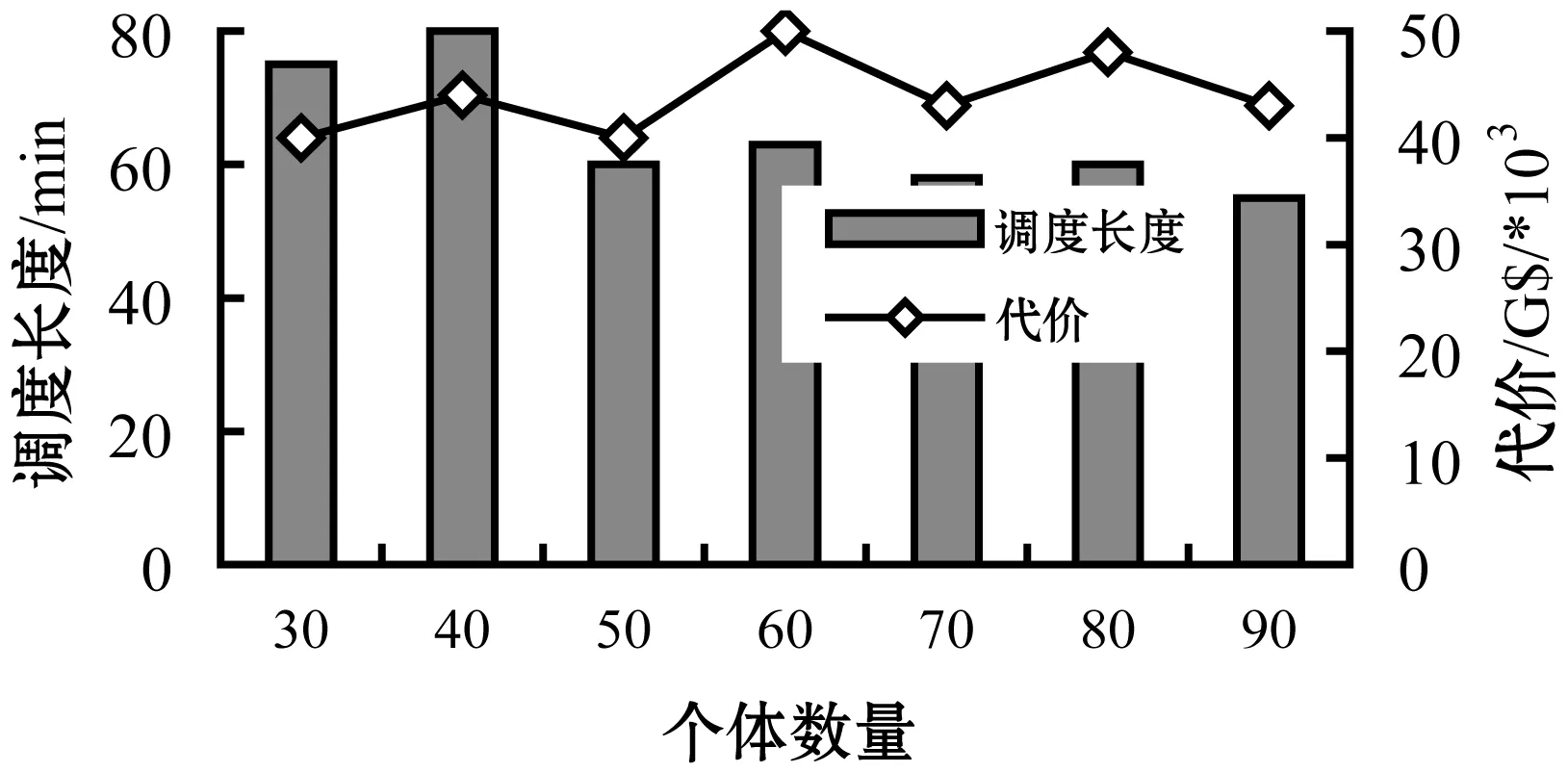
图14 个体数量对调度长度和代价的影响

4 结 语

针对工作流任务调度优化问题，提出了一种云工作流任务多目标调度遗传算法。在个体编码方面，算法采用了一种二维排列编码方法。另外，在适应度设计方面，设计了一种考虑任务执行代价与最早完成时间的均衡适应度函数。同时，引入了三种遗传交叉操作和两种遗传变异操作，增加了最优解的求解概率。实验结果表明，新算法在执行代价与调度效率间可以实现更好的均衡优化，是有效可行的。