银基复合材料电刷的摩擦磨损特性
2019-05-16白云路
白云路 张 强
(北京控制工程研究所,北京 100190)
文 摘 基于Archard 模型建立了电刷与导电环之间摩擦过程的磨损模型。搭建了导电环摩擦磨损试验台,对银基复合材料电刷的电接触摩擦磨损性能进行了实验验证。结果表明,大的接触压力会使表面微凸体更容易发生塑性变形而形成磨屑;载流会在电刷材料表面形成波纹状磨痕并产生粉末状的磨屑;磨损率在磨损初期会由于接触面积较小和表面加工硬化的作用出现先升后降的变化规律;对磨损率模型进行修正,使该磨损率模型对银基复合材料电刷磨损率的预测较为准确,为进一步研发银基复合材料电刷提供了理论指导和实验依据。
0 引言
太阳帆板驱动机构(Solar Array Drive Assembly,SADA)是航天器的关键组成部分,主要由步进驱动电机以及换向机构等构成。SADA 机构利用其上的导电滑环机构为航天器和太阳帆板之间提供了功率和信号传输的通道,因此是航天器上少数的单点故障源之一,其长时间持续稳定地工作对卫星寿命和可靠性有着重要影响[1-2]。
SADA 机构中的导电滑环是其中重要的换向机构,由电刷和导电环组成,其在滑动过程的磨损率,直接影响导电滑环的寿命以及可靠程度,因此了解掌握其磨损的规律对于延长寿命以及保证可靠性有重要的意义。
国内外研究成果表明,材料的磨损率由许多十分复杂素决定,根据磨损机理的不同,电刷磨损分为磨粒磨损、黏着磨损、疲劳磨损、剥层磨损和电蚀磨损[3],而区分这5 类的条件因素有: 电刷材料、摩擦副表面状态、接触压力、载流密度、滑动速度以及空间环境等[4-5]。因此,对于特定的材料和环境条件,掌握其摩擦磨损特性需要采取针对性的实验。
电刷的滑动电接触磨损主要分为两类:由于摩擦引起的机械磨损以及由于电流对材料影响而引起的电磨损。在滑动电接触材料中机械磨损特征与普通摩擦副中的磨损特性相类似[6]。与一般的机械磨损不同,电接触磨损由于存在力、电、热等多场耦合因素的影响,其摩擦磨损规律更加复杂,影响因素更多。
本文主要针对现阶段在轨使用的银基复合材料电刷的摩擦磨损规律进行研究,通过建立磨损率模型,为后续实验提供理论依据和参考。实验中重点研究的环境变量为接触压力、载流大小,根据不同工况下的实验数据,对结果以及现象进行分析,找到相应的规律,从而为选择更好的摩擦磨损工况以及更准确的预测摩擦副失效的时间节点提供帮助,同是可以为SADA 机构的生产工艺提供指导[7-9]。
1 电接触磨损率模型建立
20 世纪中期,英国莱斯特大学的教授J.F.Archard 提出了摩擦学领域著名的Archard 黏着磨损理论。Archard[10]模型对磨损过程进行了假设,认为两平滑表面在相互接触时首先发生在较为凸起的表面微凸体上,在正向载荷与相对滑动的共同作用下,微凸体发生变形,由于局部区域应力集中的作用,当超过材料的屈服强度时,就会引起接触表面微凸体的塑性变形,形成黏着结合点[11]。
图1为Archard 磨损模型示意图,假设摩擦副表面一侧的材料较软,另一侧的材料较硬;假设较软材料一侧表面微凸体的半径为a,当从材料较硬一侧施加法向载荷W 时,微凸体发生塑性变形,较软一侧材料的屈服极限与所承受的法向载荷W 存在如下关系[12]:

式中,σs为弹性材料的屈服应力;n 为微凸体数目。
摩擦副在刚开始产生相对滑动时,黏着结合点会遭到破坏,材料会从一个表面转移动到另一表面或离开表面成为磨屑,假设产生的磨屑是半径为a 的半球体,则磨屑的体积为2πa3/3,首先定义磨损率为磨损单位距离的后总的磨损体积,同时假定每个微凸体都会在相对滑动的过程中由于黏着结合点的破坏产生一粒磨屑,因此,磨损率的计算表达式为:
式中,Q 为所有磨屑的磨损体积。
将(1)式带入(2)式,化简为:

在实际摩擦磨损的过程中,只有一部分微凸体会产生磨屑,为了表示微凸体产生磨屑的机率,引入磨损系数K,加入相对滑动距离对磨损的影响,Q 可以表示成:

式中,L 为摩擦副之间的切向相对滑移距离;根据接触条件的不同,K 在10-2~10-7之间波动[13]。
弹性材料的屈服应力与其布氏硬度的关系式[14]为:σs≈H/3,因此式(4)可写成:

式中,H 为摩擦副中较软表面的硬度。
式(5)即为Archard 基本的理论模型,可以看出模型较为简单,只考虑了4 个影响因素,因此模型存在着一定的缺陷,在应用时效果很差。
值得注意的是磨损系数K 是一个较为复杂的变量,其影响因素众多,如环境温度、摩擦副表面形貌特征、润滑条件、摩擦类型等,因此需要设计针对性的实验来获得。
在本次实验中,电刷与导电环之间的接触面积会随着磨损过程发生变化,因此将摩擦接触面的面积S考虑在内,W 与S 之间的关系如下:

式中,FN为两接触表面之间的法向压力。
将式(6)带入式(5)得出:

本文根据银基复合材料电刷在摩擦过程中的磨损数据的变化规律,将电刷接触面积,载流大小等因素考虑在内,对上述模型进行修正,并计算了相关的系数,使模型具有更好的实用性。
2 实验验证
2.1 实验台的设计
根据前期理论建模的需要安排实验任务,并得出银基复合材料电刷磨损的基本特性以及规律性的结论。
实验内容有:
(1)摩擦磨损形貌观察,摩擦磨损类型判别;
(2)分析接触压力、载流大小对磨损率的影响;
(3)分析磨损行程与磨损率的关系。
根据实验内容搭建一个综合实验平台,主要组成部分如图2所示。
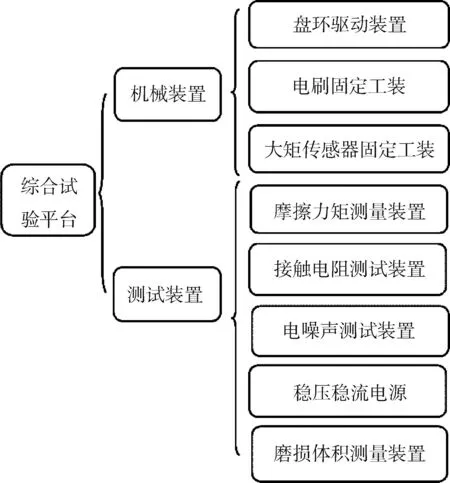
图2 载流摩擦磨损实验台系统组成图Fig.2 Composition diagram of current-carrying friction and wear system
组装实验工装并放入真空容器内,实验装置如图3所示。

图3 试验装置Fig.3 Experiment facility
2.2 装置及流程
实验中采用银基复合材料电刷和银铜合金导电环作为摩擦副,组装成实验装置。
实验中用到的装置有:
(1)导电环跑合装置;
(2)电刷及刷架固定装置;
(3)Futek 反作用式力矩传感器TFF325,最大量程为0.5 N·m;
(4)Agilent Technologes N8740A 电源;
(5)光学显微镜(用于测量并计算磨损体积)。
根据实验研究内容,制定相应的实验规划和实验流程,如图4所示。实验中采用的是块状电刷,设计的实验工装让电刷和盘环和其在SADA 机构中真实的工作环境一致,来保证得到的数据更具实用价值。
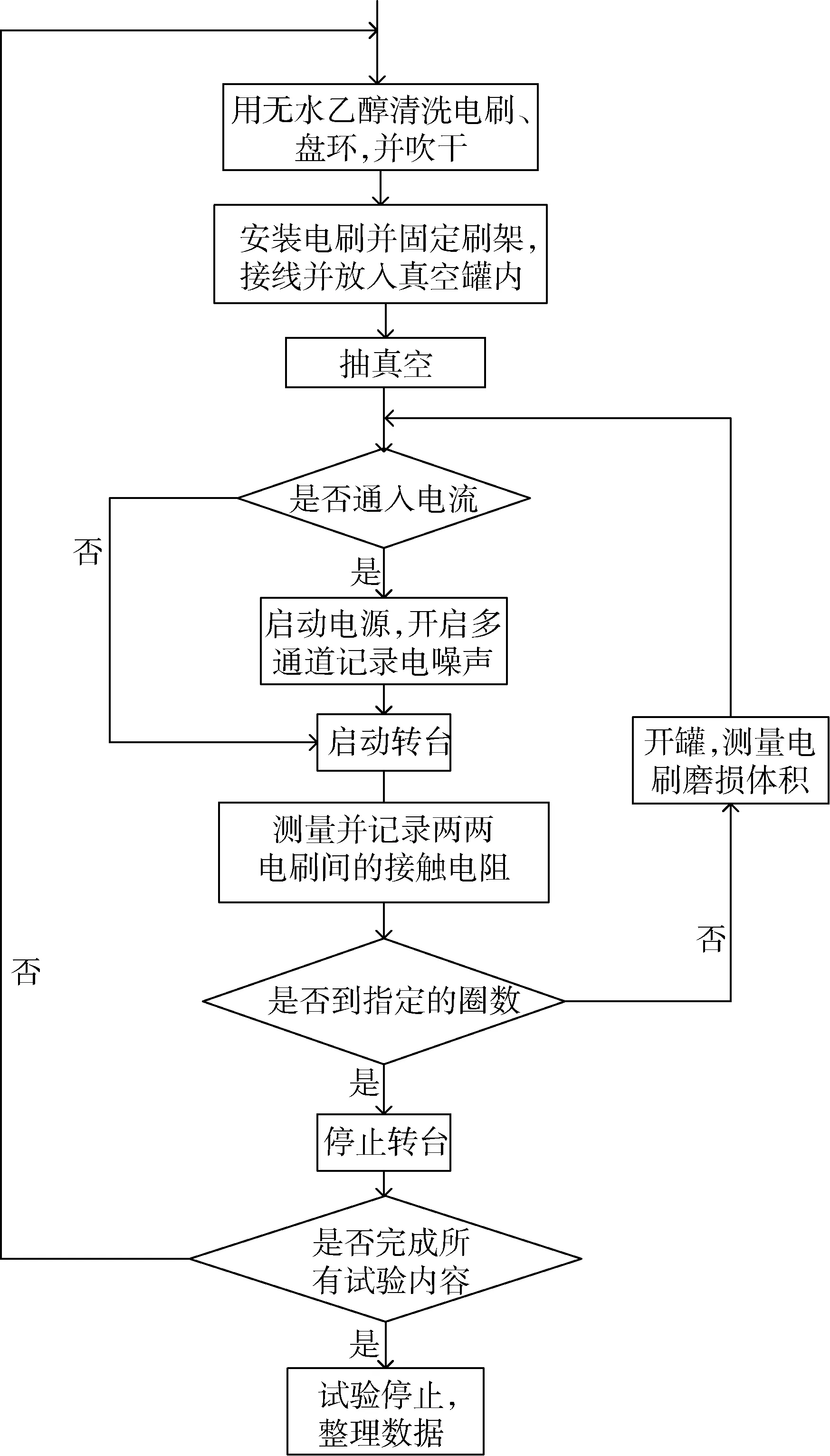
图4 实验流程图Fig.4 Flow diagram of experiment
实验中参数的设定根据SADM-2-1F 盘式导电环在实际中的工作状态,此次实验中选取的工作电流为0、3、10 A,电刷压力的选取参考SADA 机构正常工作压力进行选取0.3、0.5、0.8 N。
2.3 试验结果与讨论
根据表1中的实验结果,讨论不同工况对磨损率的影响,分析并得到磨损率随着工况参数变化的规律。
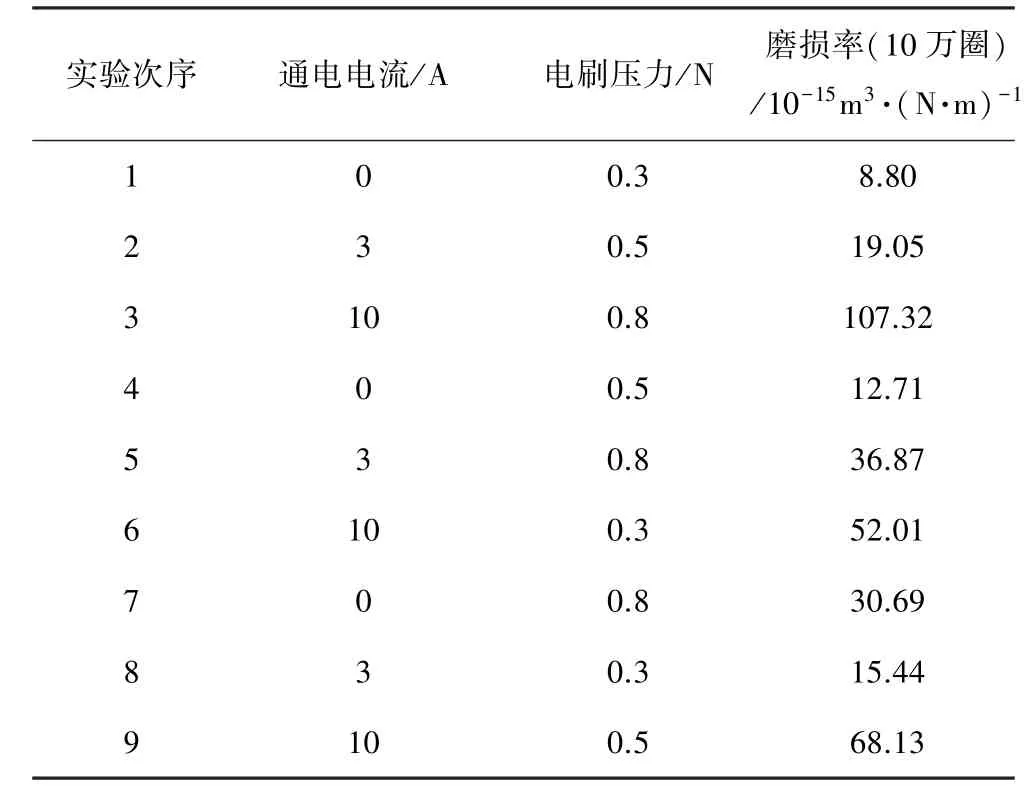
表1 不同工况下的磨损体积__Tab.1 Wear volume under different working conditions
2.3.1 电刷压力对磨损率的影响
从图5可以看出,在通入相同电流的情况下,电刷压力越大,整体的磨损率越大。这与公式(7)得出的磨损体积与两接触表面的法向压力结论一致。
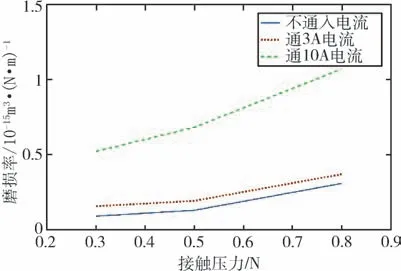
图5 电刷接触压力对磨损率的影响Fig.5 Effect of brush pressure on wear rate
从微观的角度分析其原因,金属表面的微凸体会在接触压力大的情况下更快的进入到塑性变形阶段,在与摩擦副不断的摩擦接触过程中引起微凸起接触区域应力疲劳,导致微凸体很快到达疲劳极限,从而断裂并脱落,形成磨屑[15]。同时,在高循环应力、载流的热效应等环境下,更容易发生黏着,当摩擦副表面发生相对滑动时,因微凸体的局部应力集中引起黏着节点发生剪切断裂而发生脱落,脱离表面的部分或进入摩擦副成为磨屑,或迁移到另一个对偶副的表面形成凸起,随着磨屑与表面凸起加入到磨损过程,在摩擦副表面产生沟犁作用,在滑动方向上形成不同深度的划痕,见图6、图7。

图6 磨损试验前后电刷表面的形貌 200×Fig.6 Morphology of brush surface before and after wear test

图7 磨损试验前后导电环表面的形貌 200×Fig.7 Morphology of conducting ring before and after wear test
2.3.2 载流对磨损率的影响
从图8可以看出,磨损率随载流的增大而增大。初步从微观角度对现象进行分析,主要是由于载流摩擦条件下表面由于电流的热效应温度升高,造成表面材料的软化,摩擦副表面的微凸峰更容易发生焊合和黏着,并在相对滑动过程中断裂和脱落,从而导致磨损率的增加。
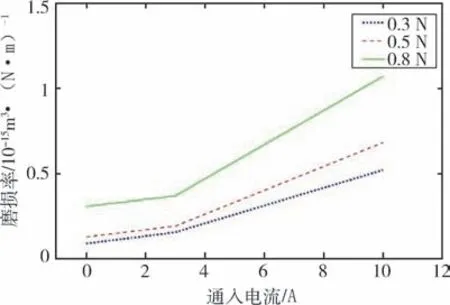
图8 载流对磨损率的影响Fig.8 Influence of the current on the wear rate
从图9可以看出,在无电流时,磨屑成较大的片状,而载流磨损中会较小颗粒的粉末状的磨屑,并且容易粘连,因此经常聚集成团,分析产生该现象的原因,是由于银基复合材料电刷的硬度较低(HB60),在摩擦热及电流引起的焦耳热的作用下,表面微凸体尖端热量较为集中,导致材料在接触过程中发生软化及变形,在接触压力作用下软化的材料表面微凸体会黏附在另一接触面上,在两表面分离时,由于微凸体较软,更容易发生塑性变形并断裂,因此断裂后的微凸体残留在另一接触面,在经过反复滑动,小的残留微凸体会发生疲劳剥落与断裂,从而形成粉末状磨屑,而软化的磨屑更易粘连在一起,形成团状的细小磨屑。同时,电刷在弹片加载情况下,接触点的不断跳动会增加电流的消耗,从而释放大量的焦耳热加速材料的软化[16]。

图9 有无载流对磨屑的影响 200×Fig.9 Shape of abrasive grains between current-carrying efficiency
从图10可以看出,在无电流状态下,磨损表面为线条状规则的磨痕,而载流状态下,导电环的表面会形成波纹状不规则的磨痕。分析该种现象的原因,可能是由于载流下,摩擦副的软化造成两表面之间更容易产生焊合和黏着现象,当发生焊合后,一方的表面将会产生凸起,从而加剧磨损的过程,并且在该区域会加剧焊合的形成,因此焊合区域会越来越大,而波纹状的磨痕正是焊合区域的最初的形态如图11所示。

图10 有无电流对导电环表面的影响 200×Fig.10 Surface topography of conducting ring between current-carrying efficiency

图11 导电环表面的焊合区域 200×Fig.11 Welding region on the surface of conducting-ring
综上所述,沟犁磨损、疲劳磨损、表面焊合以及黏着磨损是银基复合材料电刷与银基盘环材料在真空载流滑动摩擦过程中的主要磨损机制。
2.3.3 磨损率变化规律
通过测量电刷的磨损深度进而计算出磨损率,绘制出磨损率随磨损距离的变化曲线,如图12为通入3 A 电流、接触压力为0.8 N 工况下电刷与导电环实验全程的磨损率变化曲线。
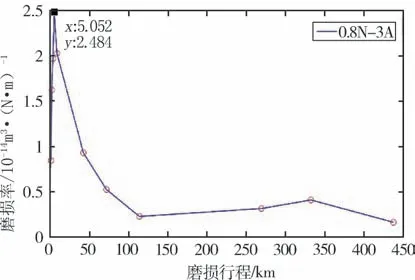
图12 磨损率随磨损距离的变化曲线Fig.12 Wear rate varies with wear distance
从图12中可以看出在试验的初期,磨损率呈现出上升的趋势,等到在5 km(12 000 圈)后,磨损率迅速下降。有两种理论可以解释该现象。
(1)在磨损刚开始时,两接触面中,电刷为抛光后的表面,导电环为精车后的表面,此时两者的表面微凸体都较为平坦,再加上电刷的压力较小,此阶段很难发生塑性变形,进而不会形成稳定的接触面。等到一定的圈数后,光滑表面的微凸体由于应力疲劳发生脱落,一方面会形成初始的磨屑,另一方面会将新的表面暴露在摩擦副之间,而新的表面是未经过抛光的表面,因此两者的摩擦系数逐渐变大,导致磨损系数K 增大,使摩擦副的磨损率上升,等到一定的圈数后,摩擦副之间才会形成了初始的摩擦表面。
(2)在金属精加工和抛光的过程中,会导致表面的加工硬化,从而使摩擦副表面比里层的金属硬度要高,随着磨损的进行,硬度低的金属暴露在摩擦副之间,摩擦副中较软的银基复合材料电刷的硬度H 会降低,会造成磨损率的增大,等到加工硬化层被磨去后,H 会趋于稳定,此时,磨损率将由其他因素决定,并进入到相对稳定的阶段。
随着摩擦副接触面积的增加,接触表面的性质趋于稳定,此时磨损系数K 接近恒定,接触面较软的电刷表面硬度值H 也趋于稳定,由Archard 磨损率公式可知,接触面积的增加会导致磨损率的降低。
为了进一步探究接触面积对磨损率的影响,先假设接触面积为长方形,如图13虚线边框所示,同时可以绘制出磨损单位深度接触面积变化率随磨损深度的变化曲线(图14),可以看出,在实验的初始阶段,接触面积的变化比磨损了0.1 mm 时的变化率大10倍以上。在磨损深度达到0.1 mm 后,接触面积的变化率下降到变化比较稳定的阶段,但是随着磨损深度的加深,接触面积还在不断的增大。通过计算可得,在磨损深度为0.1 mm 时,磨损体积为1.728 mm3,与图12的实验原始数据进行对比可知,对应的磨损路程约为5 km。
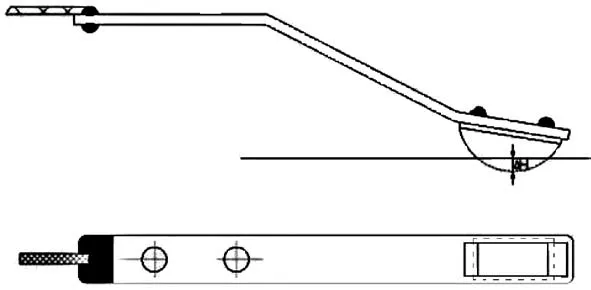
图13 磨损一段时候后电刷与盘环接触示意图Fig.13 Contact diagram of brush and slip ring after a period of wearing
理论上可以看出在5 km 以前磨损率应该下降的很快,而实际过程中确实先升后降,因此可以得出在此阶段中K、H 对磨损率的综合影响比面积大。在5 km后,K、H 对磨损率的影响开始减弱,而此时接触面积的变化接近线性递增的阶段。由于磨损体积Q与接触面积S 成反比,因此分析的结果与实验结果较为吻合。
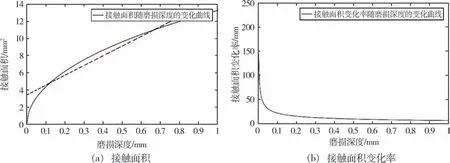
图14 接触面积、接触面积变化率随磨损深度的变化曲线Fig.14 Curve of contact area and change rate of contact area with wearing depth
2.3.4 磨损率模型修正
针对以上的实验数据的分析,取磨损行程为10万圈(45 km)建立的磨损率模型进行修正,并加入载流、接触面积对模型的影响。
通过图8可以看出,载流与磨损率之间的关系不是简单的线性关系,因此引入载流系数KI和载流指数α;同时引入接触面积因子λ、β 用于表示接触面积S 与磨损路程的比值系数。
因此式(7)变为:
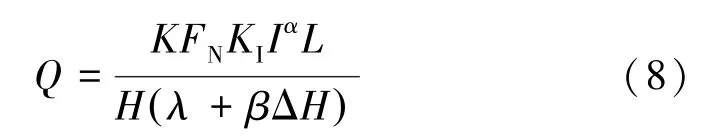
虽然在实验初期会出现磨损率增大的阶段,但由于此阶段持续时间较短,产生的磨屑总量较小,因此可以忽略实验初期对于最后磨损体积的影响。大部分磨屑产生在稳定磨损阶段,此过程中磨损率没有大的波动,磨损系数K 较为稳定,接触面积在近似线性的区域。实验中,认为平均的磨损深度ΔH 为0.62 mm,截取图14中0.1~0.5 mm 的曲线并进行线性拟合,可以得到系数β≈12、λ≈3.3。
当没有通入电流时,KI=1、α=0,此时式(8)变为:
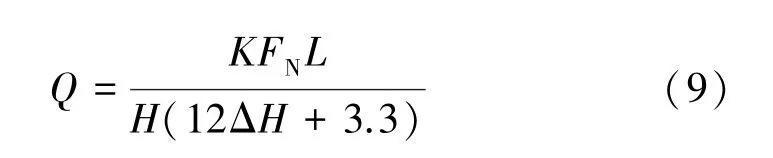
材料的硬度为HB52~64,磨损体积为在42 km(10 万圈)取得的数据,因此可以计算出3 组实验数据得到的平均磨损系数K ≈5.16 × 10-5。
当通入电流时,将表1中的数据带入(8)式,计算出4 组数据中的α 的平均值为1.04,KI的平均值为0.44。因此最终修正后的模型为:
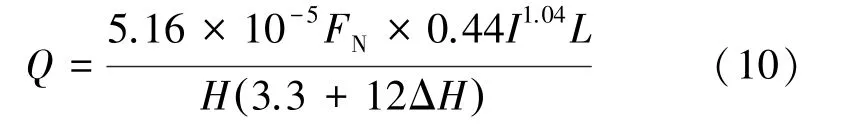
用剩余的两组实验结果作为对比,结果见表2。可以看出在0.5N-3A 条件下的预测数据与实际值较为准确,而在0.3N-10A 条件下的预测数据比实际值偏小。分析原因,一方面可能是由于实验工况数比较少,造成数据欠拟合,因而误差较大;另一方面可能是由于在载流很大时会造成摩擦副之间产生电弧等现象使磨损环境更加恶劣。
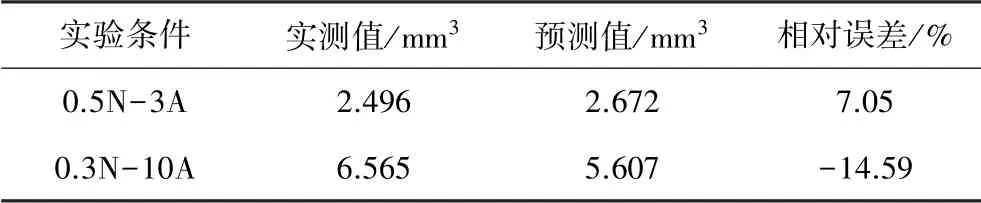
表2 磨损体积实际值与预测值的对比Tab.2 Contrast between actual and predicted of wear volume
3 结论
(1)电刷的压力过大会导致摩擦副微凸体过早的由于塑性变性、应力疲劳和黏着而产生磨屑,磨屑会在接触表面由于沟犁作用形成磨痕。
(2)载流在真空中电刷与导电环滑动摩擦过程的磨损机理主要为沟犁磨损、疲劳磨损、表面焊合以及黏着磨损,产生波纹状的磨痕。
(3)实验过程中,电刷与导电环磨损初始阶段磨损率出现先升后降,为了降低此阶段产生磨屑影响机构的稳定性和寿命,需要预先磨合电刷与盘环,分析实验数据后推荐预先磨合的圈数在8 000 圈左右,即正反4 000 圈。
(4)通过实验数据,修正后的磨损率模型从预测结果可以看出,模型在载流较小时结果与实际数据较为接近,而在载流很大时,预测值离实际值较远,原因可能是在模型设计中考虑的载流因素不够全面,因此需要更多的实验分组才能进一步完善模型。
