不同聚类算法在Wi-Fi定位中的研究

陈 蕾

（浙江农林大学信息工程学院，浙江临安311300）

0 引 言

随着信息技术的高速发展，基于位置服务的应用越来越受到学界关注。以卫星导航等传统方法为代表的定位技术由于GPS等卫星信号到达地面会有所减弱，难以穿透建筑物，因此在室内很难使用卫星定位系统获得准确的定位信息，精度也不高。但是人在室内活动的平均时间约占整体的80%左右，因此室内定位的应用已逐渐成为研究焦点。

时下，通讯技术的不断进步，即使得智能移动设备日趋成为社会生活中的时尚新宠儿。根据媒体市场研究公司Zenith对52个国家和地区的调查报告研究显示，在2017年底全球智能手机普及率达63%，其中在一些领先的国家和地区，智能手机使用的普及率都已经超过了90%。智能移动设备的普及，为室内定位的发展和应用带来了更广阔前景，但同时也提出了更高的要求。

室内定位是指在室内环境中获取位置定位，常见的主要有采用无线通讯、基站定位、惯导定位等多种技术集成形成一套室内位置定位体系，从而实现人员、物体等在室内空间中的位置监控。室内定位作为国内外研究的热点，其研究成果在商场购物、交通引导、景区导览、人员设备管理、公共服务、紧急救援等方面都可见到典型应用。目前堪称主流的室内定位技术有：红外线、超声波、超宽带、蓝牙、Wi-Fi、基站、RFID技术，此外还有比较新颖的可见光通信、地磁技术、视觉定位等。不同的定位技术均有各自的优缺点，结合应用场景，选择合适的定位技术至关重要。研究可知，基于Wi-Fi技术的室内定位是现下最常见的室内定位技术，虽然在众多定位技术中Wi-Fi技术的定位精度不是很高，但由于现代生活中Wi-Fi的使用已随处可见，各类环境中Wi-Fi设施布置完备，技术相对简单，又减少了硬件设备架构的成本，因而使其在各类定位方法中仍然具有鲜明的优势。对此，本文拟展开研究论述如下。

1 基于Wi-Fi的室内定位

基于Wi-Fi技术的定位系统作为现下最常见的室内定位技术，相关的室内定位算法非常多，大体可以分为基于几何方法的定位、极大似然估计法定位和基于接收信号强度（RSSI）建立指纹库的定位。这里，对此可做探讨分述如下。

（1）几何方法。是通过测量与用户相关的几何参数来获得用户的位置。几何方法多可分为2种。一种是根据信号到达时间或到达时间差、到达角度来测算待测点与信号发生源之间的距离。另一种是利用信号传播模型来测距，常根据一些无线信道的半统计或者经验模型，利用在线测得无线信号强度估计距离。

（2）极大似然估计法。也是基于接收信号强度的Wi-Fi定位中一种主要的定位方法，极大似然估计法是建立在极大似然原理基础上的一个统计方法，极大似然定位算法则是在几何三边定位算法中加入极大似然估计原理，与几何方法有所区别，且具有较大的实用性。

（3）基于接收信号强度的指纹法定位。由于前文的几何方法受非视距传播路径影响较大，且测距成本不低，因而有研究者提出了该种定位方法。指纹法是在离线阶段将接收信号强度的某些特征与环境中的地理位置建立对应关系，构成指纹库。而后在线阶段则实时提取接收信号强度的信号特征，在指纹库中寻找对应数据，最终实现定位。相对而言，指纹法研究起来比较简单，有一定的实用研究价值。

2 聚类算法

聚类分析起源于分类学，但在此后科学技术的飞速发展中，人类对分类的实现也已从仅主要依靠经验和专业知识而衍生转变为逐步融入了数学工具的定量分析，形成数值分类学，又引入了多元分析形成了聚类分析。聚类分析内容丰富，其算法可以分为划分法、层次法、基于密度的方法、基于网格的方法、基于模型的方法等。研究内容详见如下。

2.1 K均值聚类算法

K均值（K-means）聚类算法属于划分法，该方法需要输入聚类个数k，然后对数据对象进行聚类，输出满足方差最小标准的k个聚类，同一聚类中的对象相似度较高，不同聚类中的对象相似度较低。K-means聚类是根据数据对象之间的相似度来间接聚类的，是无监督的学习方法。

2.2 蚁群聚类

蚁群聚类算法是1991年由Deneubourg提出的，而Lumer和Faieta将蚁群聚类算法模型应用到了数据分析的领域，所以蚁群聚类算法尚且还是一种比较新颖的算法。蚁群聚类算法是结合蚂蚁选择觅食路径的行为和蚁群在蚁穴中将散落的蚂蚁尸体堆积成堆来清理的行为实现聚类的。蚁穴清理的行为是蚂蚁堆越大，越吸引工蚁搬运过去，因此，数据的空间分布直接影响聚类结果。

2.3 DBSCAN 聚类

DBSCAN（Density-Based Spatial Clustering of Application with Noise）聚类算法是一种基于密度的聚类算法。该算法是在1996年由Ester等提出的一种简单又有效的聚类算法。算法可描述为：在某些空间中给定一组点，它将位置紧密靠在一起的点（与许多邻近邻域的点）组合在一起，标记为异常值点，单独存在低密度区域（其与最近的邻域点距离太远）。DBSCAN算法是对数据样本进行划分的聚类算法，且事先并不需要知道数据样本的标签，是一种非监督的聚类算法。核心点（Core Point）是指在该点的聚类半径ε中，若是含有超过设定参数MinPts数量的点，则该点被称为核心点。边界点（Border Point）是指在该点的聚类半径ε中，点的数量小于所设定的参数MinPts，那么就不属于核心点，但是该点又落在核心点的邻域之中，则称该点为边界点。噪音点（Noise Point）是指在该点的聚类半径ε中，点的数量小于所设定的参数MinPts，那么就不属于核心点，但是该点又不落在任一核心点的邻域之中，那么该点被称为噪音点。

3 实验仿真

本文实验是通过对接收到的Wi-Fi信号强度先进行聚类分析，根据分析后的特征值再输入支持向量机的回归模型，实现待测点的位置定位。文中对此可得研究详述如下。

3.1 数据来源及处理

本文实验环境为Window10操作系统，Matlab 2016a（9.0.0.341360）版本，实验数据采集自浙江农林大学B10学生宿舍楼的第二层，过程中选择在该楼层采集35个点的所有无线接入点（AP）的信号强度。待测位置RSSI值采集的设备采用IphoneX，该设备中的开发App：AirPort工具可以采集该位置所接收到的信号强度。如图1所示。

在35个采集点停留1 min左右，进行信号强度采集，共采集AP名为ChinaNet的信号强度数据2 931条，根据不同的时刻将数据进行分类，分类后数据按照AP的硬件地址进行排序，最终获得实验数据330条。

图1 AirPort工具采集Wi-Fi的RSSIFig.1 AirPort tool collects the RSSI of Wi-Fi

在330条实验数据中选取300条作为训练数据集，其余30条数据作为测试数据集，将训练数据集作为聚类算法的数据对象，进行聚类分析。再将聚类结果作为 SVM的输入参数，对应的位置坐标（x，y）中的横坐标和纵坐标作为输出参数，分别进行训练，建立SVM模型。将测试数据集作为输入参数，分别输入训练好的SVM模型，获得横坐标和纵坐标的实验数据集，输出实验结果，即为定位结果。

3.2 3种不同聚类算法的实验仿真

K-means聚类算法的实验中k取35，同坐标点数量一致，迭代5次，实验仿真结果如图2和图3所示，定位结果分析见表1。

图2 K-means聚类结果Fig.2 K-means clustering results

图3 K-means-SVM定位结果Fig.3 K-means-SVM location results

表1 K-means-SVM定位结果分析Tab.1 Analysis of K-means-SVM location results m

根据实验结果可得，使用K-means聚类分析输入数据后，获得较好的定位结果。

蚁群聚类算法的实验中k取35，同坐标点数量一致，迭代5次，实验仿真结果如图4和图5所示，定位结果分析见表2。

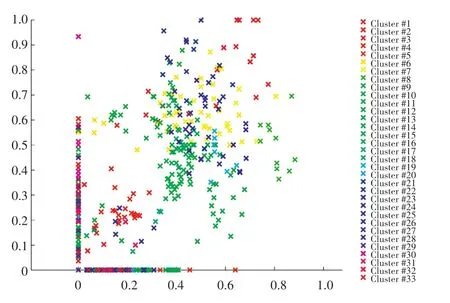
图4 蚁群算法聚类结果Fig.4 Ant colony algorithm clustering results

表2 蚁群算法SVM定位结果分析Tab.2 Analysis of ant colony algorithm SVM location results m

根据实验结果可得，使用蚁群聚类分析输入数据后，获得定位结果比K-means差。

DBSCAN聚类实验经过多次实验，选择参数邻域半径ε＝0.2，邻域样本数阈值MinPts＝3，实验仿真如图6和图7所示，定位结果分析见表3。

图5 蚁群算法SVM定位结果Fig.5 Ant colony algorithm SVM location results

图6 DBSCAN算法聚类结果Fig.6 DBSCAN clustering results

图7 DBSCAN-SVM定位结果Fig.7 DBSCAN-SVM location results

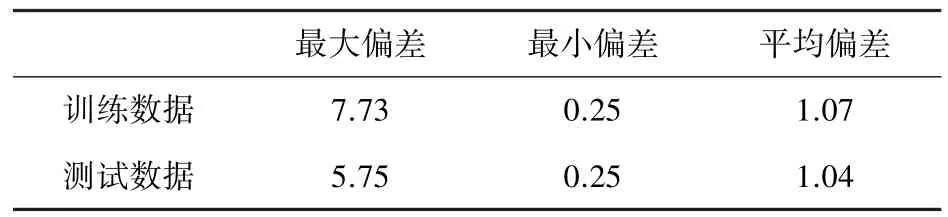
表3 DBSCAN-SVM定位结果分析Tab.3 Analysis of DBSCAN-SVM location results m

根据实验结果可得，使用DBSCAN聚类分析输入数据后，获得定位结果与K-means相差不大。

由于DBSCAN聚类能自动标识噪音点，去除噪音点后能获得较好的定位结果。但是K-means聚类虽然没有去除噪音点，定位结果仍然是3种聚类算法中最好的。

3.3 DBSCAN-Kmeans混合聚类实验仿真

研究可知K-means聚类定位结果最好，但却不能自主去除噪音点，因此会影响到实验结果。基于此，研究将DBSCAN聚类算法与K-means聚类算法相结合，先利用DBSCAN算法去除噪音点，再使用K-means聚类对去除噪音点的数据进行聚类分析。最后将聚类结果通过支持向量机的回归模型研究处理后，获得定位结果。实验仿真如图8和图9所示，定位结果分析见表4。

图8 去除噪音点的K-means算法聚类结果Fig.8 K-means algorithm with noise point removal clustering results

图9 DBSCAN-K-means-SVM定位结果Fig.9 DBSCAN-K-means-SVM location results

表4 DBSCAN-K-means-SVM定位结果分析Tab.4 Analysis of DBSCAN-K-means-SVM location results m

根据实验结果可得，混合聚类后能获得更好的定位结果。

4 结束语

本文比较分析了K-means聚类、蚁群聚类和DBSCAN聚类三种聚类算法在室内定位系统中的应用，根据在实际环境中采集的Wi-Fi接收信号强度，通过3种聚类分析，再将分析结果代入基于Wi-Fi的SVM回归定位模型相结合获得的定位结果，比较3种算法的定位精度。参照单一聚类的结果，设计提出了DBSCAN和K-means混合聚类与支持向量机的回归模型相结合的定位模型，从实验数据看，能获得更好的定位精度。