基于PLC的RS编解码器设计与实现
2019-05-16张志宇邓建晖
曾 鹏,张志宇,邓建晖
(1深圳大学,广东深圳518000;2深圳市力合微电子股份有限公司,广东深圳518000)
0 引 言
电力线通信(Power Line Communication,PLC)技术是以电力线为传输媒介,通过载波方式将数字或模拟信号进行数据的传输。为保证数据传输的稳定可靠,欧洲的PRIME联盟在窄带G3-PLC协议和宽带 PLC 协议中增加了 RS(255,239)全码[1]。 本文研究了RS(255,239)的编解码原理,用Verilog语言研发设计,利用Modelsim10.1进行仿真并给出功能仿真结果,结果表明该编解码器符合预期功能。
1 RS编码器
1.1 RS 编码算法
RS码是具有很强纠错能力的多进制BCH码,能够纠正多个随机错误[2]。RS码用生成多项式g(x)的根描述,参与编码的全部元素都在伽罗华域GF(28) 上。
RS(255,239)的本原多项式P(x)=x8+x4+x3+x2+1,生成多项式:g(x)=x16+118x15+52x14+103x13+31x12+104x11+126x10+187x9+232x8+17x7+56x6+183x5+49x4+100x3+81x2+44x+79。
RS(255,239)编码算法分 3 步,具体如下:
(1) 将消息多项式u(X) 乘X16得m(x)=m238x254+m237x253+…+m0x16。
(2)用m(x)除以g(x)得到余式r(x)=r15x15+r14x14+…+r1x1+r0。
(3)生成码字C(x)=m(x)+r(x)=c254x254+c253x253+…+c1x1+c0。
1.2 RS编码器仿真结果
图1中,clk表示时钟,data拉高表示信息有效,enable拉高表示编码有效,x表示参与编码的信息,y表示编码后的信息,参与编码的数据为 1,2,..238,239,编码后信息位保持不变,校验位为 37,133,..79,148。

图1 RS(255,239)编码器仿真结果Fig.1 Simulation result of RS(255,239) encoder
2 RS解码器
2.1 RS 解码算法
RS解码器系统结构如图2所示,可以分为5步,具体如下:
(1)由接收到的数据计算伴随式S(x)。
(2)由伴随式S(x)计算错误位置多项式σ(x)和错误求值多项式ω(x)。
(3)由错误位置多项式找出错误位置xi。
(4)由错误位置多项式σ(x)和错误求值多项式ω(x)计算各个错误位置xi的错误值Yi。
(5)得到错误位置xi和该位置的错误值Yi后,与接收的数据进行异或得到正确的数据信息,将校验码去除后发送到下级模块。
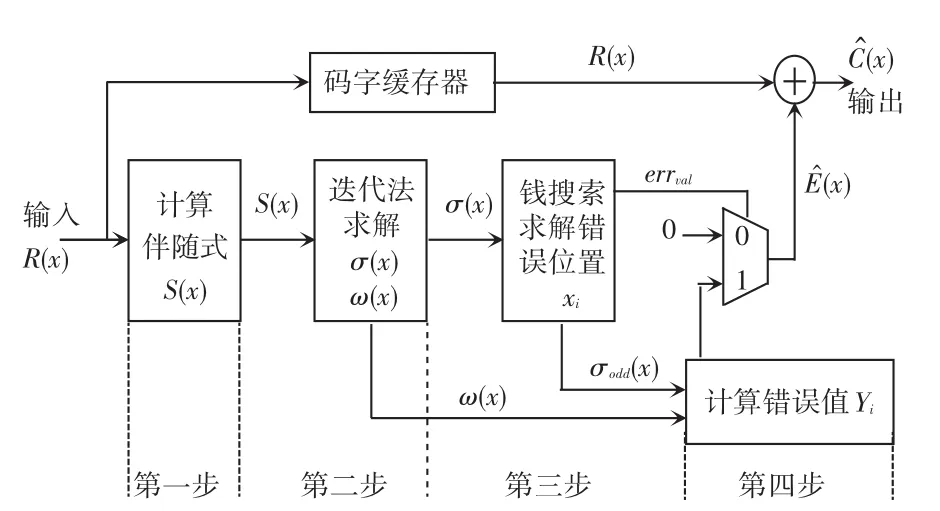
图2 RS解码器系统结构图Fig.2 System architecture of RS decoder
2.2 求解伴随式 S(x)
伴随式S(x) 的系数si计算公式为[3]:
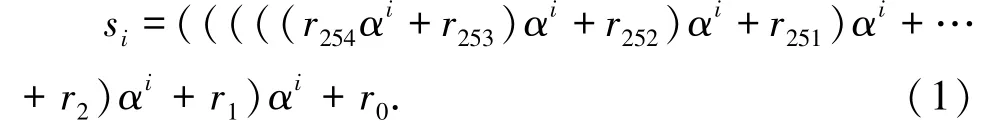
由式(1)可知计算每个伴随式系数si只需要一个域乘法器、一个域加法器和一个寄存器,关键路径延时由一个域乘法器和一个域加法器组成。
2.3 Berlekamp Massey 算法求解 σ(s)和 ω(x)
求解错误位置多项式σ(x)和错误求值多项式ω(x)采用Berlekamp Massey算法,算法流程详见如下[4]。
(1)初始化:

(2)下面的步骤依次进行循环迭代,直到k=16。研究可得对应的数学公式表述如下:

2.4 钱搜索求解错误位置xi
设接收码字R(x)=rn-1xn-1+rn-2xn-2+…+r1x+r0,要判断rn-l是否有错,只要检验σ1αl+σ2(αl)2+…+σv(αl)v=-1(v≤8) 是否成立即可,结果为-1 说明rn-l有错,否则无错[5]。
2.5 Forney算法求解错误值Y
错误值Yi的计算公式为[6]:

其中,为错误位置多项式σ(x)的根,σodd()为错误位置多项式奇数项之和,因此该项可以在钱搜索求解错误位置的同时一并得出。
3 RS解码器仿真结果
3.1 求解伴随式仿真结果
图3是求解伴随式仿真结果,编码完成后,在接收的第 1、2、3、10、11、12、13、14 个信息处添加噪声noise,信息添加噪声信号后,解码器收到的码字为11、22、29、4、5、…、9、99、79、148,y0~y15存储s1~s16的值,最终在enable信号拉低的时候计算出了伴随式 105、19、4、..、100、98、129。
图3 求解伴随式仿真结果Fig.3 Simulation result of calculate syndrome
3.2 Berlekamp Massey算法仿真结果
Berlekamp Massey算法仿真结果如图4所示。将伴随式s1、s2、…、s15、s16输入 Berlekamp Massey 算法模块,开始迭代时count为0,每次phase0产生一个脉冲,进行一次数据更新,最终在count为15且phase0为1的时候计算出了错误位置多项式σ(x)和错误求值多项式ω(x),可将其分别写作如下数学形式:
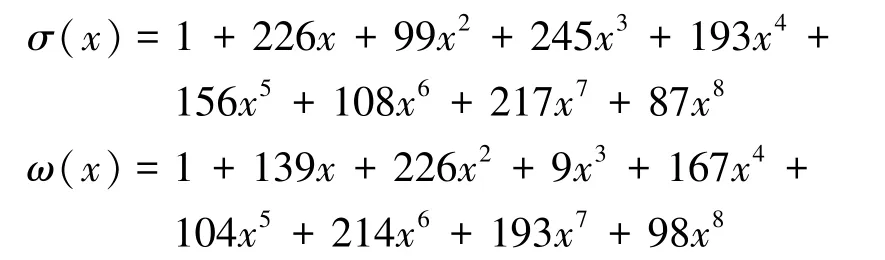
此外,算法最后还给出了σ(x)的最高次幂exp_max,为检错做准备。
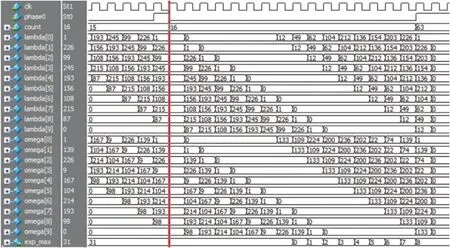
图4 Berlekamp Massey算法仿真结果Fig.4 Simulation result of Berlekamp Massey algorithm
3.3 钱搜索仿真结果
利用钱搜索对错误位置多项式σ(x)进行验根,结果见图5。chien_search拉高表示开始验根,拉低表示结束验根,当求解出σ(x)的根时,拉高val_err,可以观察到钱搜索成功地确定了错误值的位置为 1、2、3、10、11、12、13、14,在钱搜索的同时计算出了式(6)的分母σodd()并确定了错误个数cnt_val,将cnt_val的值和Berlekamp Massey的输出值exp_max做比较,若两者相等就说明错误数在纠错能力范围内,则解码器进行纠错;若两者不相等,则错误数超过纠错能力范围,不进行纠错并给出提示。

图5 钱搜索仿真结果Fig.5 Simulation result of Chien search
3.4 求解错误值和纠错仿真结果
当chien_search信号拉高,也就是开始钱搜索时,激活码字缓存器的读使能信号rdreq,将码字q从缓存器中读出,同时将错误值err与其做异或运算,得到解码后的输出rs_out,其仿真结果如图6所示。可以观察到,经过解码后,被噪声干扰的数据已经恢复,当解码结束后,即产生chien_end脉冲。

图6 求解错误值和纠错仿真结果Fig.6 Simulation result of error value solution and error correction
4 结束语
本文阐述了RS(255,239)编解码器的算法原理并用Verilog运行实现,利用Modelsim10.1进行编解码器的功能仿真,结果表明该编解码器设计正确,最大纠错能力为8。
