Volume Di ff erence Inequalities for the Polars of Mixed Complex Projection Bodies
2019-05-15HanBoZhangYuanyuan2andWangWeidong
Han Bo,Zhang Yuan-yuan,2and Wang Wei-dong,2,*
(1.Department of Mathematics,China Three Gorges University,Yichang,Hubei,443002)
(2.Three Gorges Mathematical Research Center,China Three Gorges University,Yichang,Hubei,443002)
Communicated by Rong Xiao-chun
Abstract:In this paper,based on the notion of mixed complex projection and generalized the recent works of other authors,we obtain some volume difference inequalities containing Brunn-Minkowski type inequality,Minkowski type inequality and Aleksandrov-Fenchel inequality for the polars of mixed complex projection bodies.
Key words:mixed complex projection body,polar,volume difference,Brunn-Minkowski type inequality,Minkowski type inequality
1 Introduction
The classical Brunn-Minkowski theory,that is,the theory of mixed volumes,is the core of convex geometric analysis.It originated with Minkowski[1]who combined the mixed volume with the Brunn-Minkowski inequality.The Brunn-Minkowski theory has been extended to the LpBrunn-Minkowski theory,which combines volume and a generalized vector addition of compact convex sets introduced by Firey[2]in the early 1960s and is known as Lpaddition.Lutwak initiated the new LpBrunn-Minkowski theory in[3]–[5].
In contrast to the Brunn-Minkowski theory,in the dual theory,convex bodies are replaced by star-shaped sets,and projections onto subspaces are replaced by intersections with subspaces.Lutwak et al.[6]−[7]and Ludwig[8]made great e ff ort on an Orlicz-Brunn-Minkowski theory.The theory is far more general than the LpBrunn-Minkowski theory.The Orlicz extension is based on the asymmetric LpBrunn-Minkowski theory developed by Ludwig,Haberl,Schuster,Reitzner and others(see[9]–[12]).In[6]–[7],Lutwak,Yang and Zhang established two fundamental affine inequalities in the new Orlicz-Brunn-Minkowski theory,that is,the Orlicz-Busemann-Petty centroid inequality and the Orlicz Petty projection inequality.
The dual Orlicz-Brunn-Minkowski theory for star bodies were enforced firstly by Zhu et al.[13]and late by Gardner et al.[14].They established the dual Orlicz-Minkowski inequality and the dual Orlicz-Brunn-Minkowski inequality.Moreover,Zhu et al.[13]introduced Orlicz intersection bodies and proposed the Orlicz-Busemann-Petty problem.
In[15],Abardia and Bernig defined the mixed complex projection and established some geometric inequalities.We follow ideas of Abardia and Bernig,obtain some volume difference inequalities including the Brunn-Minkowski type inequality,Minkowski type inequality and Aleksandrov-Fenchel type inequality for the polar of mixed complex projection bodies.
Let K denote a convex body(compact,convex subset with non-empty)in n-dimensional Euclidean space Rn.The set of all convex bodies in Rnis written as Kn.Let Knodenote the set of convex bodies containing the origin in their interiors.We write B for the unit ball centered at the origin and Sn−1for unit sphere in Rn.We also use V(K)to denote the n-dimensional volume of the body K.
If K ∈ Kn,then its support function,hK=h(K,·):Rn→ (−∞,∞),is defined by(see[16]–[17])

where x ·y denotes the standard inner product of x and y.Obviously,h(λK,·)= λh(K,·),where λ is a positive constant.The concept of projection body was introduced by Minkowski in the late nineteenth century to early twentieth century.For K∈Kn,the projection body of K,ΠK,is the origin-symmetric convex body whose support function is defined by(see[16])

where all u ∈ Sn−1and S(K,·)is the surface area measure of K.
Mixed projection bodies were introduced in the classical volume by Bonnesen and Fenchel[18].They are related to ordinary projection bodies in the same way that mixed volumes are related to ordinary volume.
For K1,···,Kn−1∈ Kn,the mixed projection body, Π(K1,···,Kn−1),is defined by(see[16])

for u ∈ Sn−1.Here S(K1,···,Kn−1,·)is the mixed surface area measure of K1,···,Kn−1.
Since the late 60s of the last century,Petty[19],Schneider[20]and Bolker[21]have renewed interest in the research of projection bodies.The research of projection bodies and mixed projection bodies have attracted many scholars’attention,a wealth of researches collected in two good books(see[16]and[17]).
The theory of real convex bodies has a long history and still be a very active field now.Until recently the situation with complex convex bodies began to attract attention(see[22]–[28]).
In[15],Abardia and Bernig studied projection bodies in complex vector space.The real vector space Rnof real dimension n is replaced by a complex vector space Cnof dimension n.We denote by||·||Kthe norm corresponding to the complex convex body K ∈ Cn:

We identity Cnwith R2nusing the standard mapping

The unit ball B in Cnis denoted by

Its volume is denoted by w2n.
The mixed complex projection bodies were defined by Abardia and Bernig[15]:Let K1,···,K2n−1be convex bodies in Cnand C ⊂ C be a convex subset.The mixed complex projection body ΠC(K1,···,K2n−1)is the convex body whose support function is defined by

where C·w={cw|c∈C},w∈Cn.
If K1= ···=K2n−i−1=K and K2n−i= ···=K2n−1=L,then the mixed complex projection body ΠC(K1,···,K2n−1)is written as ΠC(K[2n − i− 1],L[i])with i copies of L and 2n−i−1 copies of K.For the mixed complex projection body ΠC(K[2n−1],L[0]),we simple write ΠCK.
Further,Abardia and Bernig[15]proved the Brunn-Minkowski inequality,Minkowski inequality and Aleksandrov-Fenchel inequality for mixed complex projection bodies as follows.
Theorem 1.1[15]If K,L,K1,···,K2n−1∈ K(W),where W is a complex vector space of complex dimension n≥3,then
(a.1)(Brunn-Minkowski type inequality)

Here,K+L is defined as Minkowski addition.
(a.2)(Minkowski type inequality) For 0≤i<2n−1,

If K and L have non-empty interior and C is not a point,then the equality in(a.1)and(a.2)holds if and only if K and L are homothetic.
(a.3)(Aleksandrov-Fenchel type inequality)For 0≤i<2n−1,2≤k≤2n−2,

For the studies of complex projection bodies,also see[29].In 2015,corresponding to Theorem 1.1,Liu et al.[30]established the following polar forms of complex projection bodies.
Theorem 1.2[30]Let W be a complex vector space of complex dimension n≥3,if K,L,K1,···,K2n−1∈ K(W),and C ⊂ Cnis an origin symmetric convex subset,then
(b.1)(Brunn-Minkowski type inequality)
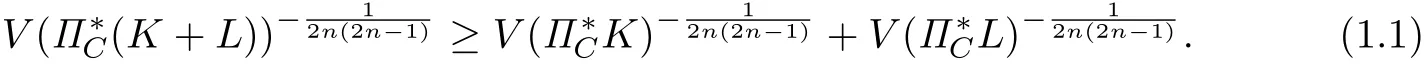
Here,K+L is defined as Minkowski addition.
(b.2)(Minkowski type inequality)

If K and L have non-empty interior and C is not a point,then the equality in(b.1)and(b.2)holds if and only if K and L are homothetic.
(b.3)(Aleksandrov-Fenchel type inequality)For 2≤k≤2n−2,

Volume difference was firstly introduced by Leng[31]in 2004.It was showed as follows:Let K and L be two compact domains.If D⊂K,then we can define the volume difference function of K and L by

The following Brunn-Minkowski and Minkowski type inequalities for volume difference functions were established by Leng[31].
Theorem 1.3[31]Suppose that K,L and D are compact domains,D′is a homothetic copy of D and D⊂K,D′⊂L.Then
(c.1)(Brunn-Minkowski type inequality)
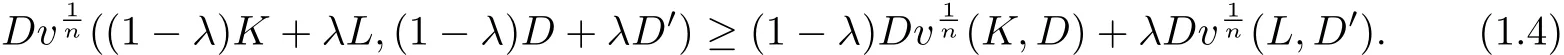
By the definition of the volume differences,substituting K and L for(1 − λ)K and λL,at the same time substituting D and D′for(1−λ)D and λD′,the inequality can be written as follows:

(c.2)(Minkowski type inequality)

where V(K,L)denotes the mixed volume of K and L,and the equality hold in(1.4),(1.5)and(1.6)if and only if K and L are homothetic and

whereµis a constant.
The Aleksandrov-Fenchel type inequalities for volume difference functions have been given by Zhao and Bencze[32]in 2010.At the same time,Lv[33]introduced the dual volume difference function for star bodies and proved dual Brunn-Minkowski and Minkowski type inequalities.Later in 2014,Zhao[34]expanded the volume difference from the real vector space to the complex vector space,and correspondingly made Brunn-Minkowski,Minkowski and Aleksandrov-Fenchel types inequalities.
In this paper,combined with the results of Zhao[34]and Liu et al.[30],we obtain some volume difference inequalities for the polars of mixed complex projection bodies in the second section.
2 Main Theorems and Proofs
In this section,we obtain a Brunn-Minkowski type inequality,a Minkowski type inequality and an Aleksandrov-Fenchel inequality of volume difference for the mixed complex projection bodies.Here,we first give following lemmas to prove our theorems.
Lemma 2.1[35](P.38)Let a1,···,anand b1,···,bnbe two series of positive real numbers and let p<0(or 0 and then with equality if and only if Theorem 2.1 Let K,L,D,D′∈K(W),where W be a complex vector space of complex dimension n ≥ 3,and C ⊂ C.If D′is a homothetic copy of D,ΠCD ⊆ ΠCK and ΠCD′⊆ΠCL,then If K and L have non-empty interior and C is not a point,then equality holds if and only if K and L are homothetic and whereµis a constant. Proof. For W be a complex vector space of complex dimension n≥3,K,L∈K(W),C⊂C,according to(1.1): the equality in(2.3)holds if and only if K and L are homothetic. Because D′is a homothetic copy of D,thus From(2.3)and(2.4),we have If K and L have non-empty interior and C is not a point,then equality holds if and only if K and L are homothetic. Notice that and imply and Hence,together with(2.1),we can write(2.5)as follows: This yields(2.2).According to the equality conditions of inequalities(1.1)and(1.4),we see that equality holds in(2.2)if and only if K and L have non-empty interior and C is not a point,then equality holds if and only if K and L are homothetic and whereµis a constant. Lemma 2.2[36]Let a,b,c,d>0,0<α<1,0<β<1 and α+β=1.If a>b and c>d,then with equality if and only if Theorem 2.2 Let K,L,D,D′∈K(W),and C ⊂C.If D′is a homothetic copy of D,ΠCD ⊆ ΠCK and ΠCD′⊆ΠCL,and 0≤ i<2n−1,then If K and L have non-empty interior and C is not a point,then equality holds if and only if K and L are homothetic and whereµis a constant. Proof. For W be a complex vector space of complex dimension n≥3,K,L∈K(W),C⊂C,according to(1.2): the equality in(2.8)holds if and only if K and L are homothetic. Because D′is a homothetic copy of D,then Combining(2.8)and(2.9),it is easy to get If K and L have non-empty interior and C is not a point,then equality holds in(2.10)if and only if K and L are homothetic. Since combine(2.6)and(2.10),we obtain i.e., This is(2.7). According to the equality conditions of(1.2)and(1.6),we see that equality holds in(2.7)if and only if K and L have non-empty interior and C is not a point,then equality holds if and only if K and L are homothetic and whereµis a constant. Lemma 2.3[37]If ci>0,bi>0,ci>bi,i=1,···,n,then with equality if and only if Theorem 2.3 When i=1,···,2n − 1,let Ki,Di∈ K(W).If and Dj(j=1,···,r)are homothetic copies of each other,then for 0 ≤ i≤ 2n − 1 and 2≤k≤2n−2,we have Proof. For 0≤i≤2n−1,2≤k≤2n−2,according to(1.3): Because Dj(j=1,···,k)are homothetic copies of each other,it follows from inequality(1.3)that By(2.13)and(2.14),we obtain From(2.11),we get which is just the inequality(2.12).
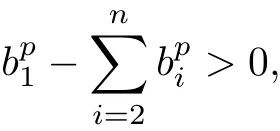






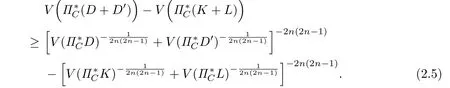

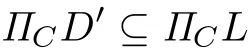
























杂志排行
Communications in Mathematical Research的其它文章
- Holomorphic Curves into PN(C)That Share a Set of Moving Hypersurfaces
- Consequence Operators and Information Algebras
- Hypersemilattice Strongly Regular Relations on Ordered Semihypergroups
- Existence of Solutions for Fractional Differential Equations with Conformable Fractional Differential Derivatives
- Hyers-Ulam Stability of First Order Nonhomogeneous Linear Dynamic Equations on Time Scales
- Long-time Dynamics for Thermoelastic Bresse System of Type III
