高温超导体的电子结构研究

彭舒婷，魏志远，赵志生，胡勇，何俊峰

合肥微尺度物质科学国家研究中心，物理系，中科院强耦合量子材料物理重点实验室中国科学技术大学，合肥，230026

目 录

I. 引言： 51

II. 铜氧化物高温超导体 53

A. Bi2Sr2CaCu2O8+δ中两种耦合模式的共存及其动量依赖研究 53

1. 两个能量结构共存的发现 53

2. 动量依赖测量 54

3. 温度依赖测量 54

4. 两能量结构随掺杂的变化 54

5. 可能的起源 55

6. 新发现对耦合模式传统理解的挑战 55

B. 在YBa2Cu3O7−x/La0.7Ca0.3MnO3异质结中发现三

维准长程电子序 56

1. 电子超调的面内分量 56

2. 电子电子序的面外分量。 57

3. 电子序的温度演变 58

4. 电子序的主要起源位置是CuO2平面 59

5. 讨论 59

C. 圆偏振光作用下欠掺杂Bi2Sr2CaCu2O8+δ位于节点处的光电子能谱 61

III. 铁基超导体：SrTiO3衬底上FeSe 薄膜高温超导体 63

A. 背景介绍 63

B. 单层FeSe/SrTiO3薄膜超导体中产生高温超导性的电子结构 64

C. 单层FeSe/SrTiO3薄膜材料的退火处理和Tc 的提高 67

D. 单层FeSe/SrTiO3薄膜从绝缘体到超导体转变的电子结构证据 69

E. 单层和双层FeSe 薄膜在电子结构以及超导性上的差异 72

F. FeSe/SrTiO3薄膜超导性质总结 76

IV. 总结与展望 76

参考文献 76

I. 引言：

超导现象的发现要追溯到1911 年Onnes 将金属汞冷却到4.2 K 附近时，其电阻突然跳跃式下降到仪器无法测量到的最小值[1]。Onnes 声称发现了一个新的物质态，他称之为超导态。然而在随后的研究中所发现的材料的超导转变温度始终不高，直至1986年Bednorz 和Muller 发现了La-Ba-Cu-O 氧化物[2]，其临界温度在35 K，揭开了超导电性研究的新篇章。随后朱经武、吴茂昆和赵忠贤等为代表的研究组分别独立做出了临界温度在90 K 左右的Y-Ba-Cu-O，掀起了高温超导的研究热潮[3,4]。2008 年以来，另一类新的高温超导体–铁基超导体被成功发现[5−10]，为高温超导体的研究提供了新的平台。2012 年，薛其坤研究组成功在SrTiO3衬底上生长了单层FeSe 薄膜[11]，可能具有很高的超导转变温度。由于其结构简单，引起了研究人员们的极大兴趣。

为了揭示高温超导的机理，一个重要的研究方向就是理解高温超导体内部的电子结构及各种电子序。在这个过程中，角分辨光电子能谱仪和共振X 射线散射扮演了重要的角色。角分辨光电子能谱仪简单说来就是利用光电效应[12]，将光照射到样品表面时，材料内部的电子吸收了入射的光子，能量便被提高了，从而被激发离开样品表面，随后到达分析器。而分析器可以记录接收到的电子的能量和动量。如果将所有角度发射的电子集中在一起，光电子在动能中的分布就可以有效的映射出电子结构的态密度(DOS)，其中包括靠近费米能的价带和能量较深的芯能级(Core levels)。我们只要读出谱图中对应峰的能量，再根据光电效应能量守恒方程反推，就能得到材料中对应的电子结合能。在实现能量分辨功能的过程中，我们只在光电效应部分用到了能量守恒。实际上在整个实验过程中也存在着动量守恒，当我们对其中的守恒量进行详细分析时，就可以获得大量材料内部电子的动量信息，进而达到动量分辨功能。共振X 射线散射，对于获取材料电子结构信息，尤其是揭示材料中的电子序，起着重要的作用。在弹性散射(REXS) 实验中，X射线光子与电子和离子晶格交换动量，以获得有关电子电荷分布的信息。与广泛用于结构研究的常规X 射线衍射不同，在REXS 中，光子能量被调谐到元素特定共振吸收线之一，这导致其对价电子的灵敏度大幅增强，能够检测CuO2平面内的电子密度分布非常小的变化，这很难通过使用非共振方法来实现。

具体而言，目前人们主要从两个角度来对铜氧化物高温超导的内在机制进行探究，其一是研究材料内部的多体相互作用[13−16]，如电子–玻色子耦合，可能充当超导配对的“胶水”。第二角度是从掺杂莫特绝缘体出发，研究相图中各种奇异量子态及它们跟超导的关系。在电子–玻色子耦合方面，本文介绍在高温超导体Bi2Sr2CaCu2O8+δ中发现两个能量结构在大范围动量空间中共存[17]，并且它们奇特的动量依赖给我们目前对于高温超导中电子耦合模式的理解带来了新的挑战。在对奇异量子态的研究中，本文介绍在La0.7Ca0.3MnO3(LCMO) 衬底上生长的YBa2Cu3O7−x(YBCO) 薄膜内部发现的三维准长程电子序[18]，这一发现揭示了铜氧化物超导体中电荷密度波的不同种类以及YBCO/LCMO 异质结中超导性和铁磁性之间的长程邻近效应。而在对电荷密度波的进一步研究过程中，理论上提出了可能具有手征对称性的电荷密度波。如果存在这种具有手性的电荷密度波，用不同圆偏振光进行测量时，应该出现差异。本文介绍运用角分辨光电子能谱仪，利用圆偏振光对铜氧超导体Bi2212 中赝能隙的测量结果[19]。实验表明，在2% 的误差范围内并未发现不同偏振光带来的差异。这对可能存在的手性电荷密度波及其强度带来了很强的实验限制。

在铁基超导方面，对电子结构的研究也扮演了重要作用。近年来发现的SrTiO3(STO) 衬底上生长的单层FeSe 薄膜由于其既具有所有铁基超导体中最简单的晶体结构（结构单元），又可能具备最高的超导转变温度Tc，而引起了人们极大的兴趣。本文将介绍在FeSe 薄膜材料中进行的系统的实验研究[20−23]。首先，通过角分辨光电子能谱对单层FeSe/STO 薄膜电子结构进行测量，得到其产生高温超导所需的电子结构；然后，通过退火，对系统引入载流子，得到了65 K 的超导能隙关闭温度；在此基础上，系统的掺杂研究揭示了绝缘体到超导体转变的电子结构证据；同时为进一步探索其高温超导产生的物理机制，作者对单层FeSe 薄膜和双层FeSe 薄膜进行了对比研究，确定了二者在电子结构以及超导性上的差异。

以下将从铜氧化物超导体和铁基超导体中的FeSe薄膜两个方面展开综述。

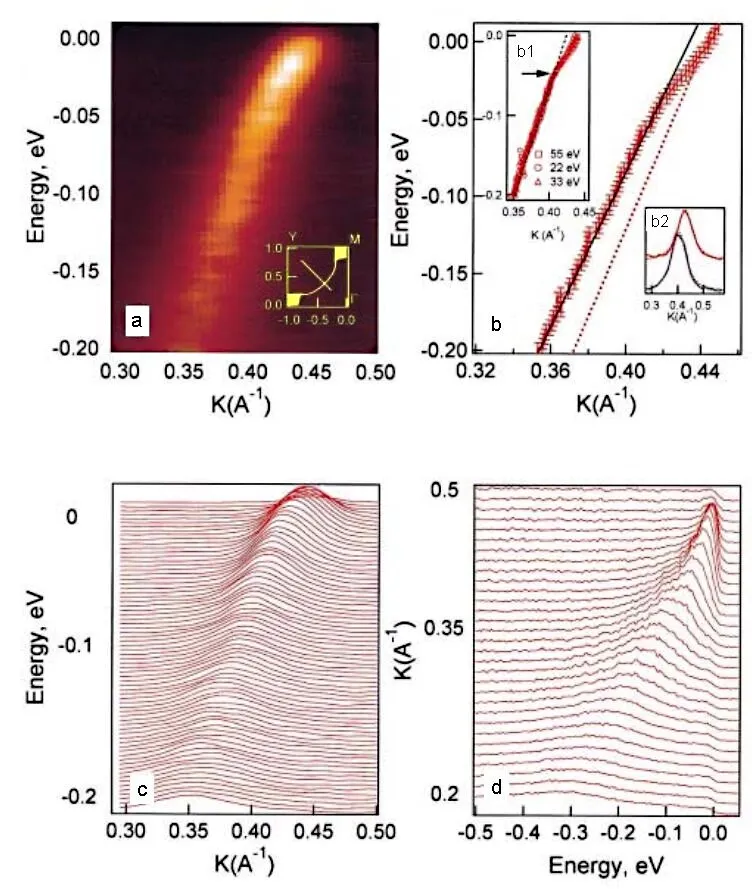
图1. Bi2Sr2CaCu2O8材料中在节点区域发现能带扭折引自文献[24]

II. 铜氧化物高温超导体

A. Bi2Sr2CaCu2O8+δ 中两种耦合模式的共存及其动量依赖研究

针对于铜氧化物高温超导体的内在超导机理，电子–玻色子耦合一直被人们所重视，有人认为其可以作为超导配对的“胶水”，而电子玻色子的耦合可能会带来能带的扭折。2000 年初铜氧化物高温超导体中节点区能带扭折(∼70 meV) 被发现[24−29]，随后反节点区∼40 meV 的能量扭折也被发现了[30−34]，因此两能带扭折的起源和其演变关系一直是争论的焦点。然而随着角分辨光电子能谱分辨率的逐渐提高，以及一系列系统研究的开展[35−37]，电子–玻色子耦合问题和两能带扭折间的动量演化问题得以解决。

1. 两个能量结构共存的发现

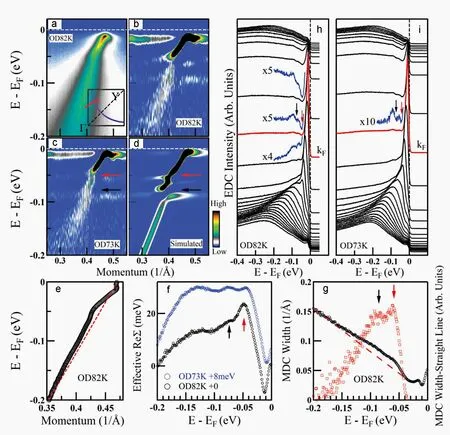
图2. 发现两个共存的能量特征。(a) OD82K 样品在17 K下测量结果。(b) 和(c) 分别是OD82K 和OD73K 样品的二次微分结果。(d) 模拟单粒子谱函数的二次微分结果，其考虑了在50 meV 和78 meV 下两个爱因斯坦玻色子与电子耦合，如两个箭头所示[38]。(e) MDC 拟合OD82K 样品的色散。(f) OD82K（黑色圆圈）和OD73K（蓝色圆圈）的有效电子自能实部。(g) OD82K（黑色圆圈）的MDC 半高宽随能量的变化和为了凸显结构而减去直线（红色虚线）的结果（红色方块）。(h) 和(i) 能量分布曲线（EDC）显示了OD82K 和OD73K 的多个峰–谷结构。引自文献[17]

作者对Bi2Sr2CaCu2O8+δ(Bi2212) 材料中的节点区和反节点区的能量扭折进行了测量。图2(a) 显示了温度为17 K 时在过掺杂（OD）82K Bi2212 样品中沿着偏离节点的动量方向测量的结果。可以首次识别出两个能量结构共存的特征。在为了增强能带可见性，作者对实验结果进行二次微分，在二次微分图像中（图2(b) 为OD82K 样品，图2(c) 为OD73K样品），谱重出现在两个不连续的位置（谱重的低谷），伴随着两条白线（谱重峰值）在主带的左右两侧。同时能量结构可以通过电子自能反应，实部通过拟合动量分布曲线(MDC) 获得定量的能带色散（图2(e)），通过减去直线的经验裸带（图2(e)中的红色虚线），作者可以得到有效电子自能实部（图2(f) 为OD82K 和OD73K）。在自能实部中出现两个峰：在∼50 meV 处的一个强峰和在∼78 meV附近的另一个弱峰，从而证明了存在两个能量结构共存。虚部还可以从相应的MDC 宽度中辨别出两个结构的特征（图2(g)）。特别是，能量分布曲线(EDC)中（图(2h) 和图(2i)） 显示了一个明显的多个“峰–谷”结构，其中有两“谷”的位置可以清晰地看到。以上实验证明确实存在两个能量共存，此后为了方便起见，作者将∼50 meV 处的能量结构称为LW 能量结构，而将另一个∼78 meV 处的能量结构称为HI 能量结构。

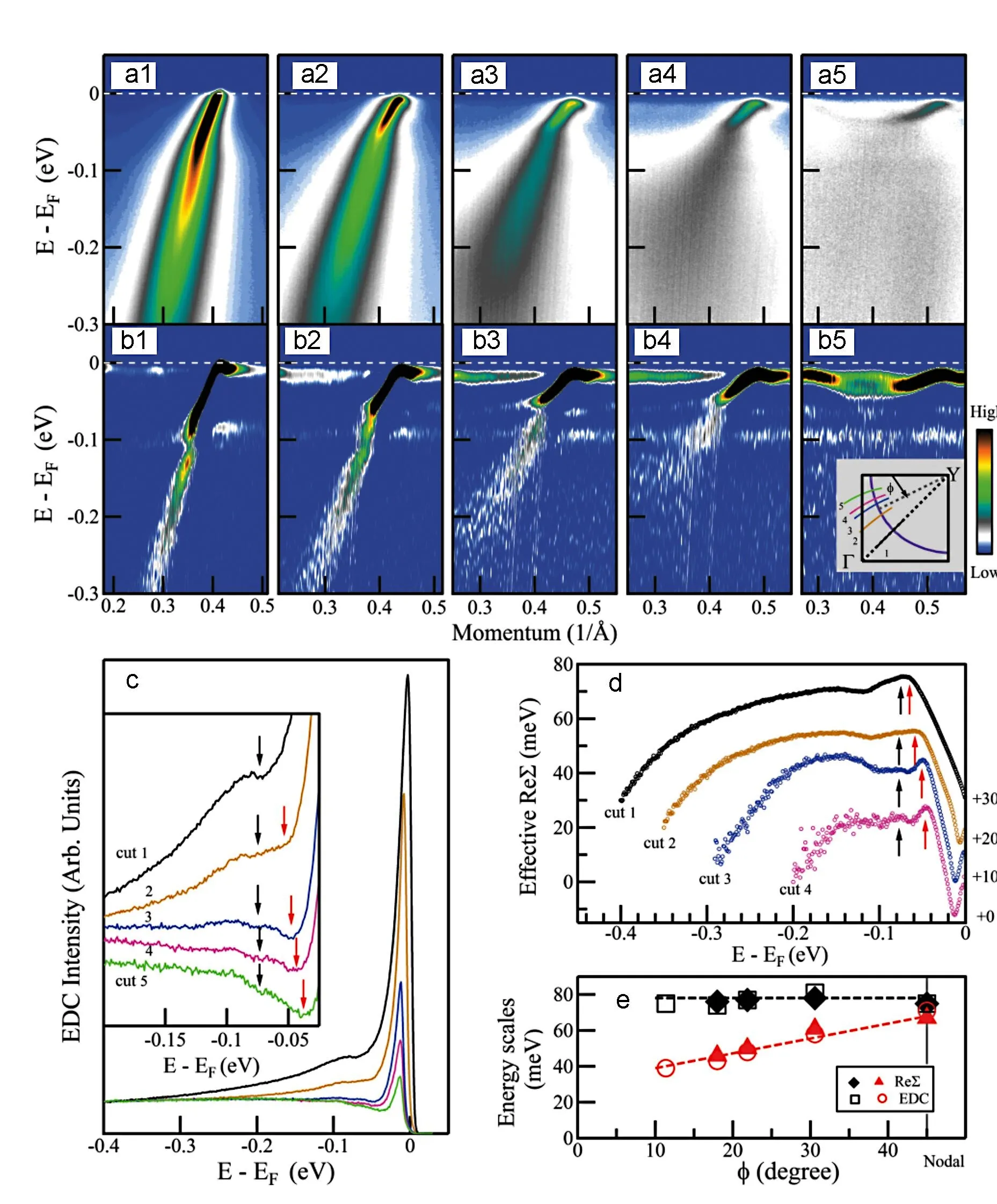
图3. Bi2212 OD82K 样品中两个能量结构的动量依赖性。(a1)-(a5) 为17 K 时沿着五条不同动量测量线测量的能带结构。(b1)-(b5) 对应二次微分结果。插图中显示了五个动量测量线的位置。(c) 沿着不同动量测量线测量时费米动量处的EDC。黑色和红色箭头指向两个能量结构。(d) 沿动量测量线1-4 得到的电子有效自能实部[38]。为清楚起见，将它们垂直偏移，右侧显示偏移值。(e) 两个能量结构的动量依赖性，从电子有效自能实部（实心菱形和三角形）和EDC中的谷的位置（空心圆和正方形）所得。引自文献[17]

2. 动量依赖测量

作者对OD82K 样品进行了详细的动量依赖的ARPES 测量，以研究两种能量结构如何从节点区域演化到反节点区域。图3(a1)-(a5) 显示了沿五个动量方向测量的数据，它们相应的EDC 二次微分结果在图3(b1)-(b5) 中。除了完全沿节点方向，其中两个能量结构太接近无法区分外（图3(b1)），两个共存的能量结构在其他图像中都是清楚的。同样的除了节点方向之外，两个“谷”的结构在其他的所有测量中费米动量处的EDC 中显示出来（图3c）。这两个能量结构也可以在有效电子自能实部中被识别出来（图3(d)）。有趣的是，LW 和HI 能量结构表现出不同的动量依赖性。图3e 总结了从有效电子自能实部的峰值和相应EDC 的谷的位置确定的这两个能量结构的位置。HI 能量结构保持在∼78 meV 附近并且随着动量变化很小，而LW 能量结构随动量变化很明显，从节点区∼67 meV 减少到反节点区域附近的∼40 meV（ϕ ∼12◦的动量方向）。

3. 温度依赖测量

与温度相关的测量提供了关于两种能量结构的不同性质的进一步信息，如在三种典型动量方向的不同温度下测量的电子有效自能实部所示（图4）。HI和LW 能量结构在进入超导状态时表现出显着的超导诱导电子自能变化。然而，它们的温度依赖行为是不同的。首先，如温度引起的自能量变化所证明的那样，两个能量结构的耦合强度表现出强烈的动量依赖性（图4(g)-(i)）。对于在反节点区域附近动量测量线3，超导诱导的自能变化主要体现在LW 能量结构上（图4(i)）。当移动到动量测量线2 时，两个能量结构的变化都比较明显，但是当动量从反节点向节点区域移动时，LW 能量结构的耦合强度似乎变弱。对于动量测量线1，我们可以看到超导诱导的自能量变化和在正常状态下HI 能量结构的明显存在。但很难确定这种变化是由HI 还是LW 能量结构引起的，因为它们的能量太接近了。其次，这两种能量结构在Tc上下表现出不同的温度依赖性。从图4(g) 和4(h) 中可以清楚地看出，即使在正常状态下也存在HI 能量结构。温度引起的自能量变化在Tc以上就开始出现，例如图4(g)中的90 K，这表明HI 能量结构可能由∼70 meV 声子引起。相反，在正常状态下没有观察到LW 能量结构的明确特征（图4(i)）只有进入超导态后明显的自能增强才会出现（如50 K 及以下的数据）。

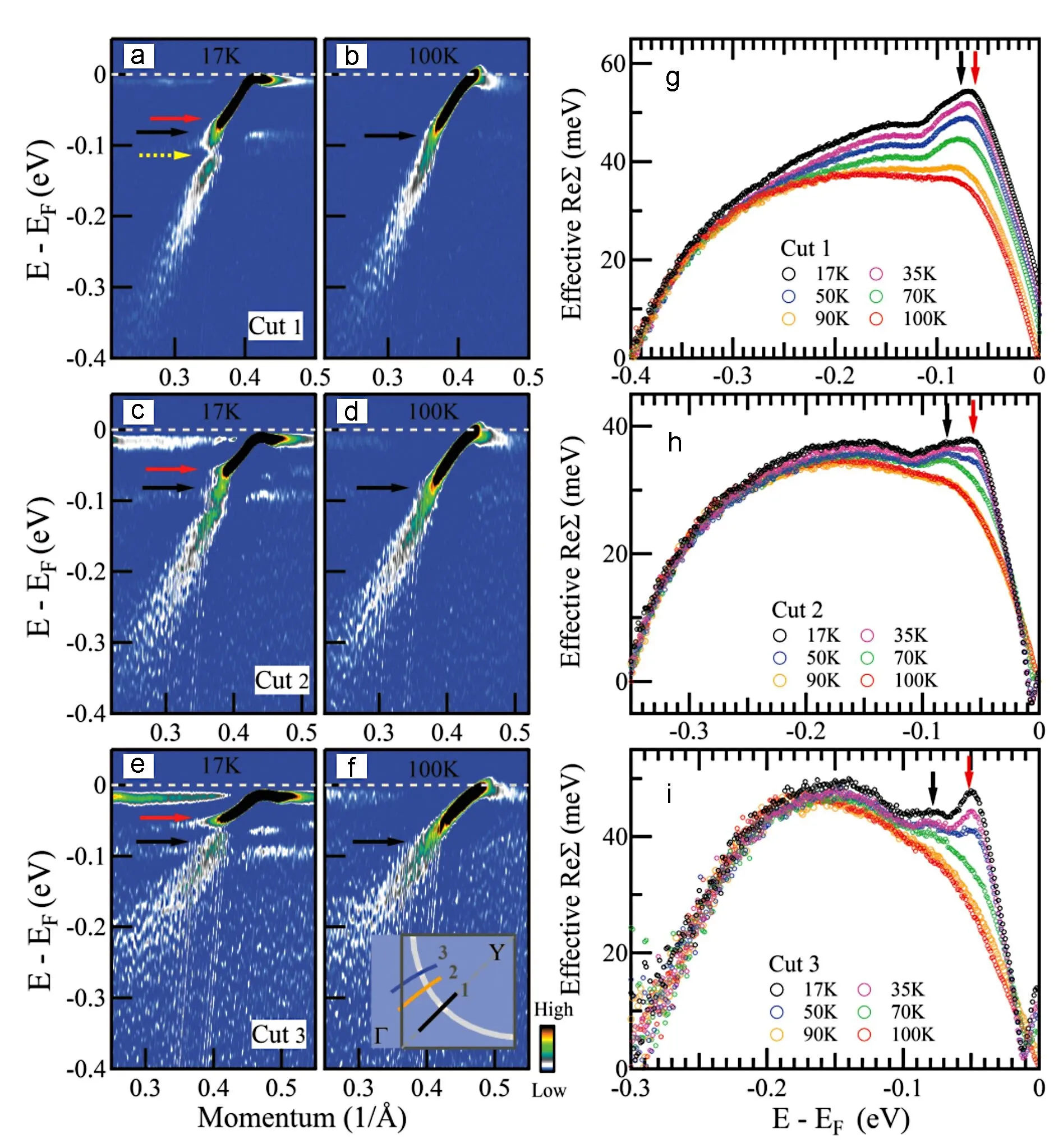
图4. Bi2212 OD82K 样品中的两种能量结构的温度依赖性。(a)、(b)为沿着动量测量线1 在(17 K) 和高于Tc 的（100 K) 测量结果的二次微分图像。(c)、(d) 和(e)、(f)分别是动量测量线2 和3 对应的结果。(g)-(i) 是动量测量线1、2、3，分别在不同温度下测量的电子有效自能实部。对于给定的动量测量线，连接100 K 色散上的高结合能点和其费米能级kF 的直线被视为所有温度共同的经验裸带[38]。两个能量峰值的由箭头标记，红色表示LW 能量结构，黑色表示HI 能量结构。引自文献[17]

4. 两能量结构随掺杂的变化

图5(a)-5(c) 显示了Bi2212 过掺杂OD）82 K，最佳掺杂(Opt)91 K 和欠掺杂(UD) 89 K 样品沿着几个动量方向测量得到的电子有效自能实部。图5(d) 是沿着ϕ = 18◦（ϕ 的定义如图3(a) 所示）方向测量得到的KF处的EDC。在Opt91K 样品（图5(b)）和UD89K 样品（图5(c)）中的LW 能量结构以及动量依赖关系与OD82K 样品（图5(a)）中的测量结果相似。当从节点区域移动到反节点区域时，它们的能量逐渐减小（图5(e)）。在Opt91K 和UD89K 样品中，HI 能量结构的特征显得相当弱，但仍有迹象表明它是存在的。我们还可以观察到在Opt91K 和UD89K样品的EDC 中的两个”谷”的结构（图5(d)），表示HI 结构可以延伸到欠掺杂区域。可以看出HI 结构具有掺杂依赖，其在过掺杂区域中得到加强。

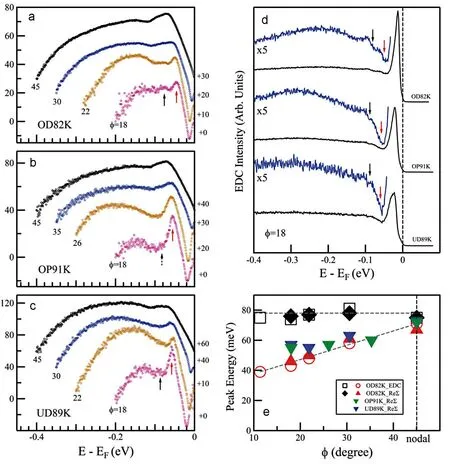
图5. Bi2212 样品中两种能量结构的掺杂依赖性。(a)-(c) 分别为OD82K 样品、Opt91K 样品和UD89 样品超导状态下测量的电子有效自能实部[38]。动量测量线的位置由图3(b)中定义的ϕ 角给出。(d) 为三个样品中ϕ = 18◦时KF 处的EDC。 (e)具有不同掺杂水平的Bi2212 中两种能量结构的动量依赖性的总结。引自文献[17]

5. 可能的起源

现在来看看超导状态下这两种共存的能量结构的起源，特别是它们到底对应着一种还是两种尖锐模式的电子耦合。理论计算结果表明，电子与一个尖锐的玻色子模式（能量为Ω0）耦合，再加上反节点区能量为E(π,0) 的范霍夫奇点作用，可以在电子自能上带来两个奇点，分别位于Ω0+E(π,0) 和Ω0+∆0，其中∆0为超导能隙[39]。由此产生的两个能量尺度将与动量无关，它们的能量差E(π,0）−∆0将会是一个常数。实验观察到两种能量结构的不同动量依赖性（图5(e)）使这种单模式耦合不太可能。它们指向具有两种尖锐模式的电子耦合。这可以通过模拟具有两种尖锐玻色子模式电子耦合的单粒子谱函数来更好地说明（图2(c)）[38]。即使用如此简单的模型模拟也和作者测量结果（图2(b)）有很多相似之处，并且模拟图像告诉我们耦合模式的能量正好对应着电子有效自能实部的峰，以及EDC 中的谷的位置。

6. 新发现对耦合模式传统理解的挑战

作者目前的工作清楚地表明，在大动量空间中存在两个独立的能量尺度，并且从节点∼70 meV 扭折向反节点∼40 meV 扭折的演变不是先前认为的单模式演化。HI 能量结构不会随动量变化很大，而LW 能量结构从节点区域附近的∼70 meV 变为反方向区域附近的∼40 meV。在节点区域，通常所指的70 meV 扭折实际上由两个能量接近的共存能量结构所组成。在反节点区域附近，40 meV 扭折很明显，因为LW 模式的耦合强度占主导地位。作者的观察结果对目前我们对铜氧超导体超导状态下耦合模式的理解提出了新的挑战。在传统的图像中，电子–玻色子耦合几乎与动量无关，如果在正常状态下存在一种耦合模式（能量为Ω） 则其能量在超导状态下会被推至Ω+∆0[39]。这种各向同性耦合图像将在整个费米面上产生能量偏移∆0，包括在像铜氧这样的d 波超导体中，局部超导间隙为零的节点区域[39]。这样的图像显然与作者的观测结果不一致。在图4(g)-(i) 中，HI 能量结构在Tc以上就已经存在于∼78 meV，在冷却到超导状态时，它几乎保持相同的能量，并且在103 meV 处没有出现新能量结构的特征（Bi2212 中OD82K 的能隙∆0∼25 meV）。尽管仍有人试图在传统图像中解释这种现象[40]，也有人提出，节点区∼7 0meV 扭折的这种在Tc上下能量不变的难题可归因于强动量依赖耦合，这种耦合为特殊的电子–玻色子耦合，具有小q的前向散射[41]，其中电子散射发生在一个小的局部动量空间中，并且正常态下的模式能量Ω 在进入超导态时，移动的能量值应该对应局域的能隙∆k[42]，因此在局部能隙为0 的节点方向该扭折不移动。虽然前向散射图像[41,42]似乎解决了节点方向能量结构不移动的问题，但随着动量向反节点方向移动d 波超导体局部能隙将增加，因此能量偏移将从节点向反节点区域增加，这与作者目前的观察结果不一致，即HI 能量结构在大动量空间内变化不大。LW 能量标度的动量依赖性更加异常，因为在这种情况下，能量结构从靠近反节点区域的∼40 meV 变化到靠近节点区域的∼70 meV不仅不同于传统耦合图像的结论，跟小q 前向散射的理论预期更是完全相反。这些观察结果表明，Bi2212的超导状态下的电子耦合模式是相当不寻常的，并需要进一步的理论研究。

通过采用高分辨率ARPES 测量，作者首次在Bi2212 的超导状态下发现了两个尖锐的电子耦合模式在大范围的动量空间共存。已知理论无法理解这两种耦合模式的异常动量依赖性，并且是对当前对超导状态下电子–玻色子耦合的理解提出了新的挑战。虽然作者目前的工作并不能说明这两种模式对铜氧超导体中的电子配对负责，但它解决了关于节点区扭折和反节点区扭折之间的动量演化关系的难题。这两种耦合模式在超导状态下明显存在，及它们不寻常的动量和温度依赖性，使得它们在电子配对中扮演着重要角色。

B. 在YBa2Cu3O7−x/La0.7Ca0.3MnO3 异质结中发现三维准长程电子序

而对于高温超导的研究中，除了电子–玻色子耦合之外，另一重要研究方向则是研究掺杂莫特绝缘体而产生的奇异量子态。如图6 所示为铜氧化合物高温超导体相图，其母体表现为绝缘的反铁磁态，随着掺杂引入的载流子（电子或空穴）逐渐增加时，反铁磁序逐渐被压制，进而产生超导相。然而在掺杂的过程中除了超导相外，更多的相也逐渐被人们所发现，如在欠掺杂区的“正常态”发现了能隙的存在，由于其在超导转变温度以上，所以被称为赝能隙。然而至今人们仍然对其产生机制有较大的争议。

图6. 铜氧化物高温超导体相图。引自文献[13]

近年来人们在赝能隙区发现电荷密度波广泛存在，并且与超导态竞争。尽管如此，仍然缺乏对不同材料中各种表现形式的统一理解。一般而言，观察到的电荷密度波分为两大类。其中一个具有接近四个晶格常数（周期–4）的面内周期性，并且已在La 基的铜氧超导体[43−45]， Ca2−xNaxCuO2Cl2[46]，Bi2Sr2CaCu2O8+δ(Bi2212)[47−49]，YBa2Cu3O7−x(YBCO)[50]，Bi2Sr2−xLaxCuO6+δ(Bi2201)[51]和Nd2−xCexCuO4[52]等材料中发现。另一类具有通常不同于四个晶格常数的变化周期，如在Bi2201[53]，YBCO[54−58]，Bi2212 [49]和HgBa2CuO4+δ[59]中发现的电荷密度波。对于块材YBCO，在共振弹性X 射线散射(REXS) 测量，以及使用零场或低场的硬X 射线衍射实验中观察到具有接近三个晶格常数（周期–3）的周期性的电荷密度波。这种电荷密度波在样品冷却时起始于约110∼160 K，并且在更低的温度下保持短程有序[54−58]。在高场下的核磁共振实验中，除了周期–3 电荷密度波外，在温度约45 ∼60 K 时发现了一个周期–4 的长程电荷密度波[60]。目前仍然不确定这两类电荷密度波是否具有相同起源，但由于各种内部（晶体环境，淬火无序）和外部（磁场）因素的影响，而产生了不同的表现形式；或者说这两类电荷密度波具有不同的起源并且都与超导态竞争[61]。

在本节中，作者报告了在LCMO 层外延生长的YBCO 薄膜中观察到的不同电子序。该电子序与块材YBCO 中的两种电荷密度波具有相似性，但表现出了重要的区别。与块材中的电荷密度波一样，电子序沿Cu–O 键方向传播，主要涉及CuO2平面中的电子态，并与超导态竞争。它具有与块材中周期–4 的电荷密度波相似的周期性，并且在CuO2平面中具有较长的相干长度，但它具有更高的起始温度，约220 K。 这些特性不同于在类似的实验条件下使用相同的REXS 技术发现的周期–3 的电荷密度波。至关重要的是，这种电子序沿着晶体c 轴显示出显着的相关性，这是目前为止在铜氧化物超导体所发现的所有电荷密度波中前所未有的。这一发现是解决高温超导难题的重要的一部分，便于深入理解铜氧超导体中的电荷密度波的多样性。此外，YBCO/LCMO 异质结中的这种三维(3D) 长程竞争序为解释该系统中报道的超导性和铁磁性之间的长程邻近效应提供了一个新的角度。

1. 电子超调的面内分量

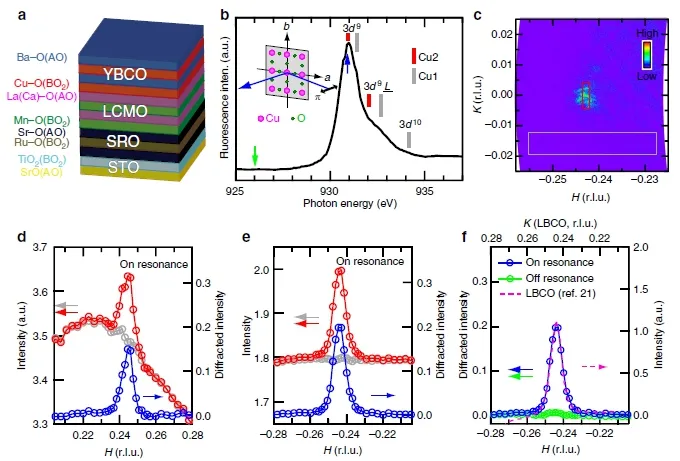
图7. 电子序的面内分量。(a)样品＃1 中异质结示意图。(b) 在Cu L3 吸收边附近测量的X 射线吸收光谱。红色和灰色条分别标记来自CuO2 平面(Cu2) 中的Cu 和Cu–O 链层(Cu1) 中的Cu 能量位置。(c) 从在930.85 eV（在(b) 中用蓝色箭头表示）测量的单个CCD 图像得到的到空间投影，显示出接近(0.245, 0, 1.38) 的衍射峰。原始图像包含L 从∼1.31 到∼1.45的范围，此处仅显示其在(H, K, 0) 平面上的投影。(d)、(e) 在固定的L=1.38 和K =0 时，在50 K 和930.85 eV 下测得的沿H 方向的散射强度。红色（灰色）曲线上的每个点表示在(c) 中由红色（灰色）矩形标记的相应CCD 图像的区域中的平均强度。蓝色曲线显示了红色和灰色曲线衍射强度之间的差异。(e) 中的强度和(d)-(f) 中的衍射强度都与(d) 中的强度具有相同的比例。(f) 在固定的L= 1.38 和K = 0 时，在926 eV（绿色曲线，由(b) 中的绿色箭头指示）和930.85 eV（蓝色曲线，与(e) 中相同）处测量的衍射强度与La1.875Ba0.125CuO4 中的测量结果[62] 相比较。所有结果均来自样品＃1。引自文献[18]

REXS 结合了X 射线衍射的周期性空间信息和对软X 射线吸收精细结构中发现的局部电子键合环境的敏感性。使用具有靠近Cu L3 吸收边（2p3/2−3d 跃迁；图7(b)）的能量的光子，REXS 可以直接检测铜氧超导体中价电子态的序，以及其涉及电荷密度和/或能带能量的调制。早期的实验表明，REXS 对电荷密度波特别敏感。

YBCO 薄膜在LCMO 衬底上外延生长。分别使用共振(930.85 eV) 和非共振(926 eV) 光子能量测量X射线散射强度的动量依赖。使用共振光子能量时如图7(c) 所示的衍射斑点在倒空间中的对称点(±0.245,0, 1.38) 处被观察到（分别如图7(d)、(e) 所示）。作者发现共振峰是叠加在强度相当的漫射背景上的。漫射背景包含来自样本的X 射线荧光成分，以及对衍射信号没有贡献的散射X 射线。如图7(d)、(e) 所示，在探测器稍微远离衍射条件的角度处测量的共振漫射背景，与除了接近H = ±0.245 处的共振峰之外的信号形状一致。通过减去漫射背景，揭示了真正的共振衍射峰（也在图7(d)、(e) 中显示出）。

这些衍射峰位于|H| = 0.245±0.005（误差棒来自确定峰值位置的不确定性），波矢非常接近1/4，表明周期接近4a 的电子序(a = 3.855˚A[54]) 沿Cu–O 键方向。这个周期性不同于REXS 在块材YBCO中发现的波矢约0.31∼0.34[54−58]，周期–3 的电荷密度波，但与NMR 研究推断出的周期性一致[50]。观察到的衍射峰半高宽δH = 0.0075，对应于电子序的相干长度ξab= a (πδH)−1∼164 ˚A（约42 个原胞长度），这是报道过的块材YBCO[57,58]中周期–3 电荷密度波最长相干长度的两倍。作者注意到YBCO/LCMO 中电子序的周期性和相干长度在数值上类似于La1.875Ba0.125CuO4[62]中的长程电荷条纹序（图7(f)）。此外，作者观察到电子序衍射峰远离共振位置而迅速减小（图7(f)）。这种强共振效应表明电子序在相当程度上涉及Cu 3d 价态。

2. 电子电子序的面外分量。

图 8(a) 显示了散射强度和附近背景强度在(−0.245, 0, L) 处关于L 的函数关系。它们之间的差值绘制在图8(b) 中以显示真实的衍射峰。衍射强度表现出对L 强烈的依赖性，表现为沿着L 方向一个半高宽为δL = 0.017 突出峰。这表明沿c 轴的电子序的相干长度约为ξc= c(πδH)−1∼219 ˚A（约19 个元胞长度；c = 11.64 ˚A）。该结果与在各种块材铜氧化物超导体中发现的电荷密度波沿c 轴方向的短相干长度（约一个原胞长度）和弱L 依赖性形成了鲜明对比。它指出了YBCO/LCMO 中存在电子序是三 维准长程有序。

衍射峰位于L = 1.38 ± 0.02，非常接近相应的波矢L = 11/8，暗示了沿c 轴的电子序的周期大约为8c。在实验上可达到的L 范围内，在相应的波矢L = 10/8 和L = 12/8 附近没有发现衍射峰。作者计算了沿c 轴四种典型周期–8 的电荷密度调制的衍射结构因子，其每个在CuO2双层内以及相邻双层之间具有不同的相位关系。这些计算的一个共同特征是，虽然相对峰值强度随调制的形式而变化，但是衍射峰只出现在L = 1/8 的奇次谐波处，在偶次谐波处不存在。计算得到的这种的定性结果与作者对电子序的面外分量的实验观察结果是一致的（参见图8(b)、(c)）。

3. 电子序的温度演变

由图9(a)、(b) 所示，作者研究了在相同的YBCO/LCMO 样品上以(−0.245, 0, 1.38) 为中心的衍射峰随温度的变化。在室温下没有发现衍射峰。它在样品降低温度时出现，其强度随着温度的降低快速增长，比块材YBCO[54−58]周期–3 的电荷密度波的强度随温度变化更加明显。这种衍射峰的出现开始于Tco∼220 K，显著高于周期–3 电荷密度波的出现温度∼150 K。Tco也显著高于磁化测量得到的LCMO层的居里温度Tm∼175 K。

在进一步降低温度后，衍射强度首先迅速增长，然后在约140 K 逐渐平稳（图9(b)）。强度在Tmax∼50 K 达到最大值，然后随着温度的降低衍射峰强度开始降低。在整个温度变化期间，衍射峰保持在大致相同的位置（图9(a)），峰宽仅有适度的变化。作者注意到，YBCO 层Tc的超导转变温度是由YBCO/LCMO 样品上的四探针电阻率测量确定的，为55±10 K（图9(b) 插图中的蓝色曲线），与衍射峰达到最大值的Tmax几乎一致（样品#1）。

图8. 电子序的面外分量。(a) 在50 K 和930.6 eV 条件下，固定H =−0.245，K =0 对样品#1 沿着L 方向测量的衍射强度结果。CCD 图像的峰值区域和背景区域中的平均强度分别以红色和灰色曲线显示。(b) 扣除背底后的衍射峰强度，即(a)中红色和灰色曲线之间的差异。(b)中的衍射强度与(a) 中的强度具有相同的比例。(c)理论计算得出的沿c 轴的一种代表性电荷密度调制的衍射结构因子。引自文献[18]

作者对第二个YBCO/LCMO 样品（样品#2）进行了类似的测量，该样品使用与样品#1 不同的界面终端生长。样品#2 显示比样品#1 稍高的转变温度Tc=72±7 K，但是Tm值相近（图9(d)的插图）。在该样品中发现了类似的电子序，其衍射峰的温度演变总体相似（参见图9(a)、(b) 与图9(c)、(d)）。值得注意的差异是Tmax，现在是∼75 K，因此作者认为每个样本中的Tmax≈Tc。

在YBCO/LCMO 中观察到的超导的出现对衍射峰的抑制使人联想到在块材YBCO[54−58]中观察到的结果。类似的温度依赖行为通常被视为两个不同序之间的微观共存和动态竞争的证据[63,64]。在完全均匀的样品中这两种序有可能共同存在，然而，更典型的情况是在样品中两个序处于相分离的状态，他们的体积分数在纳米尺度上随温度变化。无论存在哪种类型的空间共存，观察到的温度依赖性表明参与Tc以上的电子序的相当一部分电子态在Tc以下被超导态所消耗。由于涉及超导的电子态主要位于CuO2平面内，因此预测CuO2平面中的电子态将对YBCO/LCMO 中的电子序有相当大的贡献

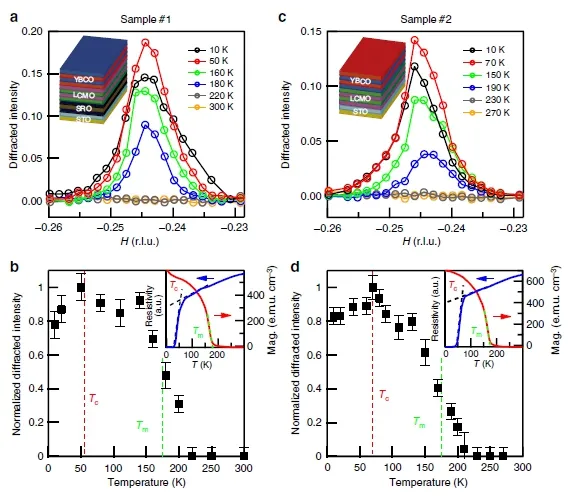
图9. 电子序随温度的演变。(a) 在不同温度下，固定L =1.38 和K =0 对样品#1 上在共振(930.85 eV)能量下沿H方向测量的衍射强度。(b) (a) 中峰值强度（归一化到最大值）的温度依赖关系。红色（绿色）虚线表示Tc (Tm)，由插图中所示的电阻率（磁化）测量确定。(c)、(d) 样品#2 的结果。(a) 和(c) 中的衍射强度具有与之前相同的比例。(a)、(c)插图：样品#1 和#2 的异质结示意图。引自文献[18]

4. 电子序的主要起源位置是CuO2平面

在ab 轴平面中周期–4 的电子序原则上可以由氧原子排列到Cu–O 链层中的满链和空链的阵列中引起。虽然据我们所知，在YBCO 薄膜中没有报道这种周期–4（也称为正交–IV）氧原子序，但在最佳掺杂及其以上的块材YBCO 中已观察到[65,66]。与其他氧原子序一样，正交–IV 序仍然远高于室温（高达500 K）并且具有弱的温度依赖性，在Tc处没有观察到异常。它在ab 轴平面中保持短程有序，沿c 轴保持弱相关，相干长度分别为∼3–6，小于一个元胞。所有这些特征都与作者在YBCO/LCMO 中的观察结果形成鲜明对比。

作者的REXS 实验提供了对链(Cu1) 与平面(Cu2) 中观察到的电子电子序的起源的进一步理解；这里作者使用参考文献[49]中区分铜原子位置（Cu1和Cu2）的术语。通过分析衍射强度的光子能量依赖性，直接探测参与相关电子序的电子态的位置，结构和轨道性质。衍射峰的这种共振曲线不同于X 射线吸收光谱。如图10(a) 所示，在YBCO/ LCMO 样品中位于(−0.245, 0, 1.38 )处测量的共振曲线显示衍射峰位于L3 的吸收最大值(931 eV) 附近。这种情况类似于块材YBCO 中的周期–3 的电荷密度波的情况，图10(b) 中可以看出[56]。 该衍射峰被认为与CuO2平面中的Cu（Cu2）的3d9基态结构（如图7b 所示）[55,56]密切相关。在作者的研究中，观察到峰值低于吸收最大值约0.55eV。类似现象在其它铜氧化物超导体中也有所发现[44−46,56,67]。作者注意到样品表面上可能存在的”死”层也许可以解释这种能量差异。这些表面层不会对散射强度有贡献，但会吸收并有效地抑制吸收最大值附近的峰值强度，从而将表观出衍射峰向较低能量移动。另一方面，如果该能量差异是固有的，则它可以对电子序的空间调制类型提供有效的约束，例如，它是否由局部电荷密度所支配。因此，YBCO/LCMO 中发现的比块材中更大的能量差异（参见图10 (a) 与图10(b)）在多大程度上可以反映出这些不同电子序的特征，是未来的一个研究方向。

接下来讨论共振谱中（图10(a)）主峰能量之上约1 eV 处的肩峰结构。由于这种能量分离作者暂时认为肩峰特征是由Cu2 中的结构所造成的（如图7(b) 所示）[18]。然而，全面的理解肩峰结构可能需要考虑所有可能的邻近状态，如Cu–O 链层中Cu(Cu1) 的3d9结构，并进行相应的理论计算。最值得注意的是，实验观察到的三维电子序可能涉及整个晶格，这将包括CuO2平面外的位置也可能对共振谱有贡献。因此，具体的定量分析共振谱谱形将成为进一步阐明电子序及其与块材电荷密度波的区别的关键。

相比之下，作者测量的共振谱与块材YBCO的Cu–O 链层中的各种氧原子序（如图10(c) 中所示[56,68]）非常不同。在这些氧原子序中，尽管其共振谱谱形细节取决于具体的氧原子序和掺杂水平，但这些共振谱的共同特征是主峰位于吸收边缘上方至少2 eV 处。该能量范围内的相关状态主要与直接受氧原子序影响的Cu1 位置上的结构相关。因为这些特征与作者观察到的特征非常不同，所以实验中观察到的电子序应该不来自于链层中的氧原子序。与温度依赖性结果一致，共振谱的这些细节也都支持CuO2平面是产生YBCO/LCMO 中电子序的主要位置。

5. 讨论

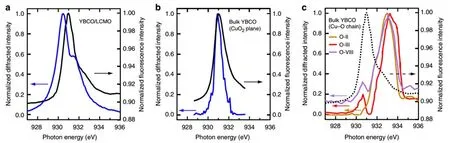
图10. 多种序的共振谱的比较。(a) 50 K 下在样品#1 上测量得到的，与电子序（共振谱；蓝色曲线）相关的位于(−0.245,0, 1.38) 处的衍射强度随光子能量的变化（归一化到最大值），与荧光（X 射线吸收光谱，黑色）相比较。(b) 从参考文献[51]再现的块材YBCO 样品中周期–3 电荷密度波的共振谱和X 射线吸收光谱。(c) 从参考文献[51,63]再现的不同块材YBCO 样品中各种氧原子序的共振谱，O–II，O–III 和O–VIII。虚线是样品#1 中的X 射线吸收光谱。引自文献[18]

作者所观察到的电子序的本质是什么？在铜氧化物超导体中，虽然有人已经提出可能存在一些非常规的序，但实验中只发现了二维(2D) 电荷和自旋序，其中面内电荷密度波波矢位于(0,0) 周围，自旋密度波波矢位于(1/2,1/2) 附近。在这种情况下，面内波矢(0.245,0) 的电子序可能是一个电荷密度波。30 nm 的YBCO 薄膜包含结构孪晶畴并具有伪四方结构，类似于Nd1.2Ba1.8Cu3O7(NBCO) 外延薄膜中的情况[69]。在X 射线束的典型光斑尺寸(100×100µm2)远大于晶畴尺寸的条件下，难以区分单轴和双轴电子序。由于Cu L3 共振光子动量相对较小，沿着H和L 方向的测量仅覆盖了倒空间中的有限范围（例如，(−0.245, 0, 13/8)是测不到的）因此不能提供足够信息来重建电子序的空间完整排布。在以后的研究中我们可以通过衍射强度对偏振的依赖性来确定改电子序具有电荷或自旋的属性，也可以通过空间分辨散射实验，来确定面内各向异性（沿a 轴与b 轴的顺序）；或者通过能够测量较宽倒空间区域的硬X 射线的衍射因子来确定该电子序的空间结构[70]。尽管有这些悬而未决的问题，作者直接观察到的这类三维电子序是首次在铜氧化物超导体中发现。

如果作者的观察确实是电荷密度波，其面内周期性与使用NMR[50]在块材YBCO 中发现的周期–4 的电荷密度波密切相关。作为局部测量手段，NMR 不容易区分层状材料中的电子序是二维还是三维的，尽管其在YBCO 上的发现已经通过假设铜氧超导体的典型二维序来解释。鉴于各种铜氧化物超导体系列中周期–4 电荷密度波的普遍存在，本实验和NMR 观测到的这两个电子序有可能反映出材料中形成相同的周期–4 电荷密度波的趋势。在这种情况下，维度、相干长度和电子序的起始温度的些许不同可能反映这种趋势对各种内部因素（应变，淬火无序）和外部因素（结晶环境，磁场）的敏感性[61]。

然而，由于在类似的实验条件下，在成分相同的材料(YBCO) 和相同的技术(REXS) 中观察到两种不同类型的（周期–3 和周期–4）电子序，导致了一个新的问题的产生：什么是造成这种差异的可能原因？找出这个原因将是了解这两种类型的电子序是否应该归因于不同来源的第一步[61]。

我们首先考虑载流子浓度。确定和控制氧化物薄膜生长中的氧含量仍然是一大实验挑战。虽然作者的沉积和退火方案针对直接在SrTiO3(001) 衬底上生长最佳掺杂的YBCO 薄膜进行了优化，但是考虑到生长过程中不同的结晶环境，在中间LCMO 层上生长的YBCO 薄膜的总氧含量可能会发生变化，这会使掺杂远离最佳水平。此外，YBCO/LCMO 界面处的电荷转移倾向于降低YBCO 层的总空穴浓度[71]。最近实验发现La0.7Ca0.3O 终止界面（与样品#1 Tc= 55 K相关）的电荷转移强于MnO2终止界面[72]（与样品#2 相关Tc= 72 K）。因此，存在周期–4 电荷密度波的样品#1 和#2 可能与块材中观察到的周期–3 电荷密度波同样位于欠掺杂区域。因此，载流子浓度对于解释上述差异可能不是必需的。

鉴于LCMO 具有磁性，我们必须考虑它们对电荷密度波的影响。作者发现电子序出现的温度Tco比LCMO 层中宏观铁磁性出现的温度Tm高45 K。然而实验发现在YBCO/LCMO 界面处的铁磁性产生的温度却略低于Tm[73]，也就不可能是Tco。因此，LCMO的长程铁磁性似乎与电子序的形成没有直接关系。在块材YBCO 中，作者注意到电荷密度波的产生与外部磁场无关。但是磁场抑制了超导性，因此可以增强接近或低于Tc的电荷密度波[55]。在YBCO/LCMO 的情况下，界面处的铁磁性或在YBCO 层中诱导的铁磁性可以通过交换场对电子序产生类似的间接影响。两者是否可以以其他不同的方式相互影响还有待探索。

因此，我们将注意力转移到应变的影响上。与块材YBCO 相比，由于SrTiO3衬底的影响，样品中的所有薄膜都受到了额外的（双轴）拉伸应变[74]。由于生长环境的变化和LCMO 层内的松弛，该应变在具有和不具有LCMO 层的样品生长之间可能经历细微变化。这些考虑可能有助于理解为什么作者在直接生长在SrTiO3衬底上的30 nm YBCO 薄膜(Tc∼60 K) 上找不到与电子序（无论是周期–3 还是周期–4）相关的衍射峰。同时，我们注意到YBCO 薄膜尚未报告存在周期–3 的电荷密度波，包括参考文献[49]中在NBCO 薄膜中发现了电荷密度波，但在YBCO 薄膜中未发现电荷密度波。对具有不同衬底和退火条件的YBCO 薄膜的系统研究可以提供一种很好的方法来阐明应变对YBCO 中电荷密度波现象的影响，以及LCMO 层是否对周期–4 电子序的出现带来了重要影响。

上述三个因素与YBCO/LCMO 异质结已知的另一种现象“超导性和铁磁之间的长程近邻效应”有关。与其他超导态—铁磁态异质结一样[75]，YBCO中的超导性和LCMO 中的铁磁性倾向于在界面处相互抑制并将它们的影响扩展到对方材料中。但是由于在YBCO 中沿c 轴的超导相干长度很短（< 3 ˚A），而LCMO 中存在高自旋极化（接近100%）和大的交换分裂(∼3 eV)，因此该异质结中两个序的相互抑制预计将被限制在界面附近(∼1 nm)。然而，一些实验已经揭示了在几十纳米的非常长范围内还存在这种相互抑制的效应[74,76−79]。理解这种不寻常的效应需要不仅仅单独考虑超导性和铁磁性。虽然电荷转移[80,81]、应变[74]、无序、缺陷[82]和三重态超导[83,84]所带来的长程影响正在争论中，但竞争序却被讨论得很少。部分原因是竞争序，如在界面处诱导的反铁磁性[73]并不是足够长程的。作者对YBCO/LCMO 异质结中与超导竞争的固有的三维长程序的发现为解决这一问题提供了一个新的角度：虽然铁磁性可能被局限于界面附近，新观察到的电子序也许可以在远离界面的区域抑制超导。这种机制是否可以解释超导性和铁磁之间的长程近邻效应还有待进一步实验。

C. 圆偏振光作用下欠掺杂Bi2Sr2CaCu2O8+δ 位于节点处的光电子能谱

包括以上研究在内的一系列实验对铜氧化物高温超导体电荷密度波展开了探索。在此基础上有理论进一步提出这些电荷密度波是否存在手性。针对这个问题作者利用基于圆偏振光的角分辨光电子能谱对欠掺杂Bi2212 系统展开了研究。

实验发现在欠掺杂铜氧化物超导体系统中，超导转变温度之上的很大范围内还存在能隙打开，这个能隙被称为赝能隙。在赝能隙中可能存在一种或多种电子序，而不同的电子序可能带来不同的对称性破缺。在ARPES 实验中可以利用左旋和右旋圆偏振光测量的差异（圆二色性）来检测对称性破缺[85,86]，而根据测量到的圆二色性的动量依赖可以判断不同种类的对称性破缺。例如，环路电流序会破坏关于Γ(0,0)−M(π,0) 反节点镜面的反射对称性，此时出现的圆二色性在反节点处 (π,0) 得到最大值[85]。另一方面，具有波矢Q = (π,π) 的反铁磁序和“d 密度波”将破坏关于Γ(0,0)−Y(π,π) 节点镜面的反射对称性[86]。除此之外，在多种铜氧化物超导体中观察到的电荷密度波[49,51,52,54]正引起人们越来越大的兴趣。有理论认为这种电荷密度波是手性的[87,88]。手性对称性破缺通常会破坏系统的所有镜像对称性，从而可以在任何镜面中测量到光电子能谱的圆二色性。

关于运用ARPES 中圆二色性来研究赝能隙中的电子序，一个突出的实验是在Bi2212 赝能隙打开温度T∗以下[89−94]，在反节点处 (π, 0) 观察到了圆二色性。这个发现首先被认为是时间反演对称被破坏的直接证据[89]，似乎与环路电流的理论建议一致[85,86]。然而，这种解释后来受到其他人的质疑，他们考虑到样品Bi–O 层中可能的超结构也会破坏Γ(0,0) −M(π,0) 反节点镜面的反射对称性（图11(a) 与图11(b) 相比），从而在反节点处(π,0)产生圆二色性[90,92,94−96]。

与Γ(0,0)−M(π,0) 反节点镜面相比，Γ(0,0)−Y(π,π) 节点镜面为研究可能的电子序提供了另一种平台。如图11(c) 所示，即使存在超结构，该节点平面仍保持镜面对称[13,96]。因此，沿Γ(0,0)−Y(π,π)节点镜面方向测量结果中是否存在圆二色性将为判断样本中可能存在的对称性破缺电子序的性质提供清晰信息。

另一个技术方面存在的重要问题来自于几何二向性，它可能掩盖了样本固有的圆二色性[90,91]。理想情况下，应该使光的传播矢量、样品表面法线和最终状态动量都在样品的镜面中。然而，在实验过程中可能存在与所需的完美实验角度的有限偏差，这种偏差会使得左旋和右旋圆偏振光测量结果产生差异，这种差异叫做几何二向性，其幅度取决于偏差大小和材料性质。这导致了一个问题：实验需要有多高的精度，才能使得几何二向性足够小，从而研究系统中本征的圆二色性[89,97]？

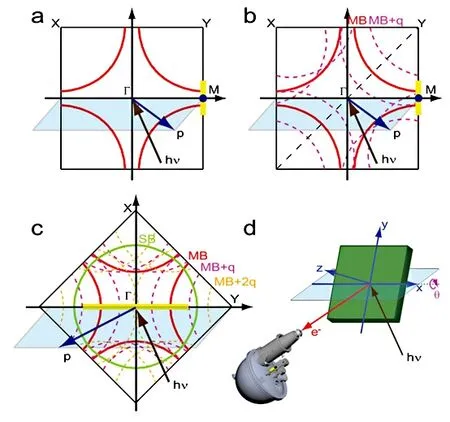
图11. Bi2212 不同镜面的光电子能谱测量示意图。(a)入射光子hµ，样品表面法线和最终状态动量p 都在Γ(0,0) −M(π,0) 反节点平面（蓝色平面）中。(b) Γ(0,0)−M(π,0)反节点平面的反射对称性随着超结构的出现而被破坏。超结构用粉色虚线表示，并标记为MB +q，以区别于主带（MB）。(c) 即使出现超结构带和阴影带（SB），Γ(0,0)−Y(π,π) 节点镜面仍保持反射对称性。MB +q 和MB +2q分别代表来自一阶和二阶超结构带的费米面。电子分析器的水平狭缝（黄线）使得能够沿着节点镜面中的Γ(0,0)−Y(π,π)动量线进行测量。(d) 光电子能谱测量的示意图和θ旋转角的定义。引自文献[19]

作者研究了在欠掺杂Bi2212（Tc= 75 K）样品的节点镜面中沿Γ(0,0)−Y(π,π) 动量方向的圆二色性（如图11(c) 所示）。低温下，在误差约2% 的范围内没有观察到圆二色性，这明显限制了该系统中可能存在的致使对称性破缺的电子序的形式。同时，作者发现该材料中的几何二向性对样品角度偏差非常敏感，小至0.3◦∼0.5◦的角度偏差足以引起相当大的几何二向性。

在实验过程中，将样品完美的对齐是先决条件。作者在大动量范围内使用费米面匹配来对齐样品[13,98,99]。借助于在费米面下可清晰分辨的精细结构（图12(a)），将样品很好地对齐，使得光的传播矢量，样本表面法线和最终状态动量均在Γ(0,0) −Y(π,π) 节点镜面中，此时几何二向性为零。如果反射对称性（不）被电子序破坏，则沿着Γ(0,0)−Y(π,π) 方向出现（零）有限圆二色性。

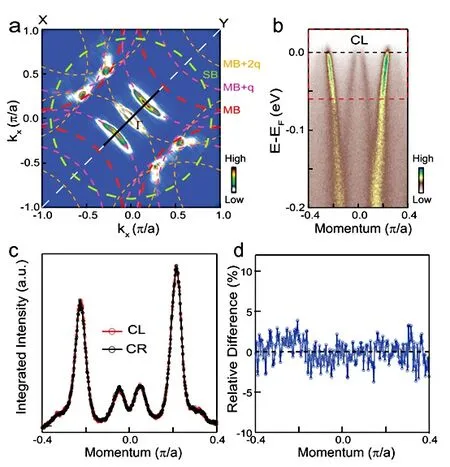
图12. 沿Γ(0,0)−Y(π,π) 节点方向不存在圆二色性。(a)通过在费米能级周围的小能量窗口[−10 meV，10 meV]上积分光谱权重而获得的费米面。虚线表示主带(MB)，阴影带(SB) 和超结构带(MB+q, MB+2q) 的理论费米面。(b)由(a) 中的黑线标记的沿Γ(0,0)−Y(π,π) 方向动量线测量的能带。(c) 对于左旋（ICL，红色曲线）和右旋（ICR，黑色曲线）圆偏振光测量光谱强度在能量范围[−60 meV，30 meV]内积分结果。积分的能量窗口由(b) 中的红色虚线矩形标记。 (d) 由(c) 中所示的能量积分光谱强度的相对差异D = (ICL −ICR)/(ICL +ICR) 可得在约2% 的水平上没有圆二色性出现。引自文献[19]

如图12(c) 所示，当动量方向完全位于Γ(0,0)−Y(π,π) 节点镜面内时（图12(a) 和12(b)），左旋和右旋光沿着整个动量线呈现相同的强度（ICL=ICR），可以在约2% 的误差内认为没有圆二色性（图12(d)）。在一种特殊的情况下，样品没有完全对齐带来的几何二向性与对称性破缺带来的圆二色性可能会在某个动量点处相互抵消产生零二色性[90,91]，但它们在整个动量线上不可能总是大小相同符号相反。因此，作者的结果表明沿着样品的节点方向没有几何二向性和圆二色性（在约2% 的误差内）。

图13. 几何二向性对角度偏移的灵敏度。引自文献[19]

为了理解实验结果的含义，作者考虑了各种电子序。有人提出，具有波矢Q = (π,π) 的反铁磁序和“d–密度波”会打破关于节点镜面的反射对称性，并在ARPES 光谱中产生圆二色性[86]。与此同时，手性对称破缺也可以产生圆二色性。这些推测与上述实验结果并不一致。然而，我们注意到这些电子序带来的圆二色性的预期值也可能低于作者的实验灵敏度。但该实验为可能存在的圆二色性设置了上限，即2%。另一种可能性是，对称性破缺电子序仅存在于具有较低掺杂水平的样品中和/或在Tc和T∗之间的特定温度区域，因为作者测量的是Tc等于75 K 的欠掺杂样品且测量在Tc以下进行。虽然需要更多的掺杂和温度依赖性测量来完全解决这个问题，但作者注意到，前人的研究在具有相似掺杂水平的样品中低于T∗的各种温度都观察到了反节点(π,0) 处的圆二色性。

沿着节点方向不存在圆二色性的特性也为研究样本几何二向性随样品角度的变化提供了独特的机会。图13 是沿Γ(0,0)−Y(π,π)节点方向附近的一些动量线的测量结果。这些动量线之间的角度差（倾斜角θ，由图11(d) 实验装置定义）在0.5◦之内。沿着这些动量线（图3(a)）在左旋(ICL)和右旋(ICR)圆偏振光测量时的光电子强度能量积分分别如图13(b)-(e) 所示。可以看到较弱的几何二向性开始出现在θ = 0.3◦处并且当θ 达到0.5◦时变得明显。作者的结果表明，Bi2212中的几何二向性对于样品小角度偏差也很敏感。

为了理解几何二向性的起源，作者考虑三步模型和突发近似下的光电子发射。光电子谱强度I和|Mf,i|2成正比，其中Mf,i≡⟨ϕF|H|ϕi⟩ 是单电子偶极子矩阵元，描述了电子从初态|ϕ⟩ 跃迁到末态|ϕf⟩[13]。当入射光为圆偏光时，偶极子算符包含了不同偏振态的矢势，分别表示为HCL（左旋）和HCR（右旋）。则圆二色性可表示为D =|⟨ϕF|HCL|ϕi⟩|2−|⟨ϕF|HCR|ϕi⟩|2[97]。如果把图11(a)中的蓝色平面定义为R 算符，那么R−1HCLR =当蓝色平面是镜面时：，因此D 值为0[97]。但是，如果存在小的角度偏差并且蓝色平面不再是镜面，则几何二向性具有非零值。在这方面，具有不同电子结构的材料，通常对角度偏差具有不同的响应。我们需要仔细考虑Bi2212 的能带结构从而在定量水平上理解该系统中几何二向性的高灵敏度。

总之，通过用圆偏振光测量Bi2212 (75 K) 欠掺杂样品的节点镜面中的Γ(0,0)−Y(π,π) 的光电子谱，作者发现在2% 的误差范围内没有圆二色性。该结果不受超结构的影响，因此明显限制了造成对称性破缺的电子序的存在形式及其强度。作者的结果还揭示了几何二向性对实验中微小角度偏差具有高灵敏度。它强调了在寻找这种材料中固有的圆二色性之前消除实验上可能带来的几何二向性的重要性。

III. 铁基超导体：SRTIO3 衬底上FESE 薄膜高温超导体

A. 背景介绍

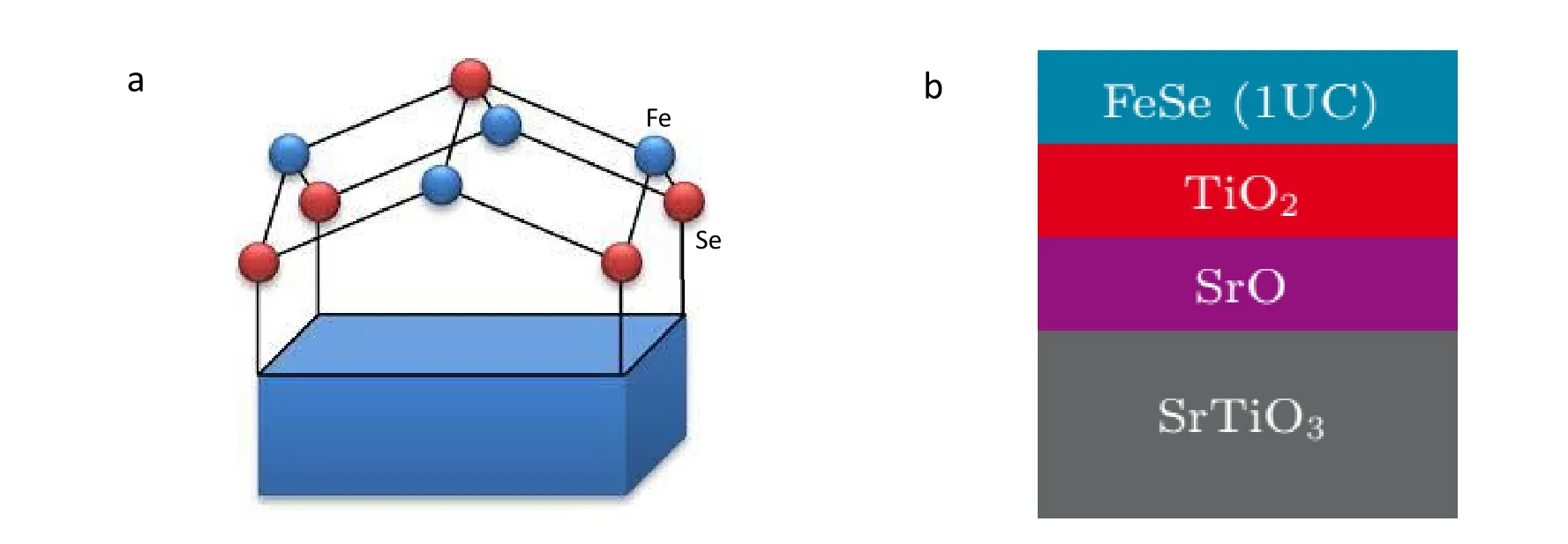
图14. SrTiO3 衬底上生长的单层FeSe 薄膜结构。(a)单层FeSe 薄膜的结构示意（蓝色：Fe 原子，红色：Se 原子）[102]。(b)FeSe/SrTiO3 薄膜及衬底的结构[11]

铁基超导体是继铜氧化物超导体之后的第二类高温超导材料，研究铁基超导体对于理解高温超导机理至关重要。人们对一系列的铁基超导块材的物理性质与电子结构进行了广泛的研究。在薄膜方面，2012 年清华大学薛其坤研究组通过MBE（分子束外延）的方法，在SrTiO3衬底上生长出单层FeSe 薄膜[11],[101]。其结构如图14 所示。对单层FeSe 薄膜的STM 测量给出的结果显示，在4.2 K 的温度时其STS 谱在费米能两侧出现了四个峰位，这些峰的位置分别在±20.1 meV 和±9 meV 处。假设20.1 meV 处的能隙是超导能隙，同时使用石墨烯上的FeSe 薄膜超导能隙和超导转变温度Tc的比值[100]，得到的FeSe/SrTiO3薄膜的超导转变温度将为80 K。对于块体FeSe 材料，其在大气压下的超导转变温度Tc约为8K[103]，通过加高压的办法，能使得其Tc达到36.7 K 左右[104]。另一种嵌插结构的FeSe 材料AxFe2−ySe2(A=K, Cs,Rb, Tl)，其在大气压下的超导转变温度Tc约为32 K[105,106]，在高压下能达到48 K[107]。所以，即使在考虑当时新发现的AxFe2−ySe2材料很高的超导转变温度后，仍然很难理解为什么单层的FeSe 薄膜材料的超导转变温度会如此之高。

因此，对单层FeSe/SrTiO3薄膜的研究就显得非常重要：(1) 它具有所有铁基超导体中最简单的晶体结构—单个FeSe 层。(2) 它可能具有铁基超导体中最高的超导转变温度。下面将详细梳理在FeSe/SrTiO3薄膜上运用ARPES 进行的一系列电子结构研究。

B. 单层FeSe/SrTiO3 薄膜超导体中产生高温超导性的电子结构

首先，作者对单层FeSe/SrTiO3薄膜超导样品的电子结构进行了测量。如图 15(a) 所示，为其费米面测量结果。为了做对比，还列出了(TI,Rb)xFe2−ySe2超导体(Tc=32 K)（图15(b)）和(Ba1.6K0.4)Fe2As2超导体(Tc= 35K)（图15(c)）的费米面[105,106,108]，同时有对块材FeSe 费米面的能带计算结果（图15(d)）。

对于单层FeSe 超导体，作者只在M (±π, ±π)点附近发现了电子型费米面（标记为γ），且没有任何迹象表明在Γ(0,0) 点存在有费米面。而作为对比的(TI,Rb)xFe2−ySe2超导体(Tc= 32 K) 的费米面存在M 点的电子型费米面γ，以及Γ(0,0) 点的电子型费米面α 和β[109−112]；(Ba1.6K0.4)Fe2As2超导体(Tc=35 K) 的费米面存在Γ 点的空穴型费米面α 和β 以及在M 点区域的复杂费米面[113−116]。同时, 块体FeSe超导体的能带计算结果表明存在Γ 点的空穴型费米面和M 点的两个电子型的费米面。实验结果表明，单层FeSe 超导体作为铁基超导这个大家族中最简单的一类体系，也有着极其简单的且不同于其他铁基超导体的电子结构。

在能带结构上（图15(e)），其布里渊区中心区域(Γ 点) 的能带结构主要由一条带顶位于费米能以下80 meV 的空穴型能带α，以及M 点的一条带底位于费米能以下60 meV 处的电子型能带γ 和一个空穴型能带β 组成。

对于材料是否超导，最直接的证据来自输运测量，但对于单层FeSe 超导薄膜来说，因为其严格的单层结构及对空气的敏感性，所以很难进行输运测量。所以，作者先利用ARPES 测量其电子结构，从而从电子结构上给出相应信息。通过对样品在不同温度下的光电子谱的测量，最终得到了单层FeSe 超导薄膜的超导能隙随温度的变化（图16(a)）。

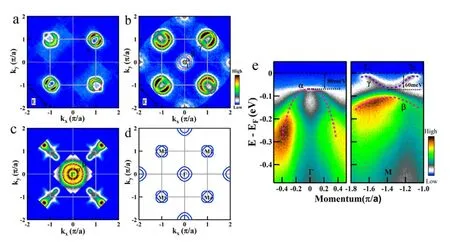
图15. 单层FeSe 超导体的费米面。(a) 在20 K 时对单层FeSe 薄膜的费米面测量表明只有在M (±π,±π) 点存在电子型的费米面γ。(b) (TI,Rb)xFe2−ySe2 超导体(Tc = 32 K) 的费米面存在M 点电子型的费米面γ 和Γ(0,0) 点的电子型费米面α和β。(c) (Ba1.6K0.4)Fe2As2 超导体(Tc = 35 K) 的费米面存在Γ 点的空穴型费米面α 和β 以及在M 点区域的复杂费米面。(d) 能带结构计算(kz = 0) 得到的β–FeSe 的费米面存在Γ 点的空穴型费米面和M 点的两个电子型的费米面。(e) 单层FeSe 超导体Γ 点和M 点的能带结构。引自文献[20]

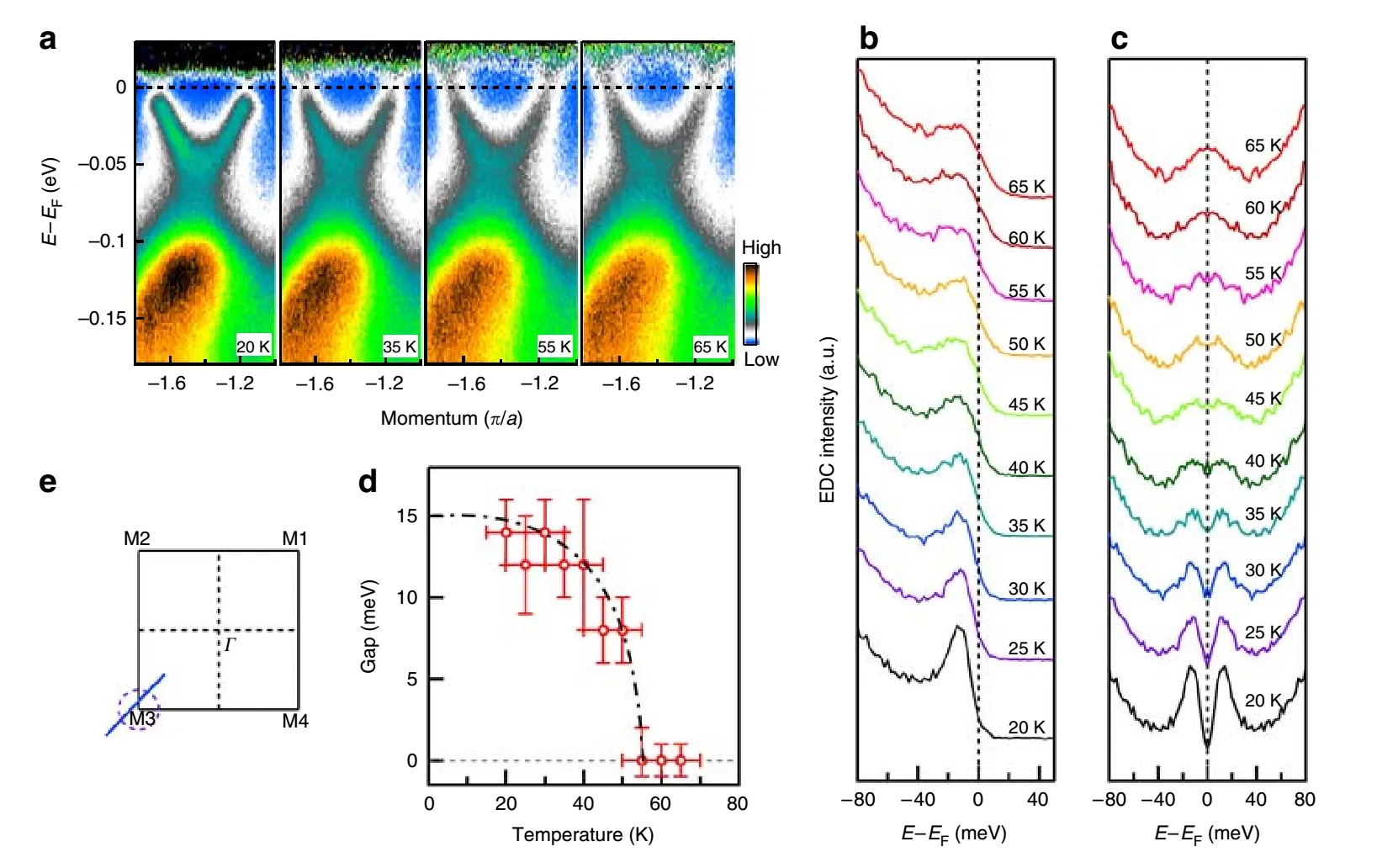
图16. 单层FeSe 超导薄膜的超导能隙随温度的变化。(a) 沿(e) 中M3 点附近的蓝色动量线测量得到的能带在不同温度下的结果。(b) 光电子谱上穿过γ费米面的能量分布曲线(EDC) 随温度的变化关系。(c) 对称处理后的EDC。(d) 超导能隙随温度的变化关系。黑色虚线是BCS 型能隙从15 meV 到0 meV 时随温度的变化关系。(e) 在M3 点附近沿动量空间进行测量的路径。引自文献[20]

与光电子谱对应的能量分布曲线 (EDC) 在图16(b) 中，但这样的曲线不便于观察超导能隙的变化，为了消除在费米面附近费米分布的影响，按照铜基超导体中常用的方法，将原来的EDC 沿费米能处进行对称化处理，得到图16(c) 的对称化EDC[117]。对于M 点附近的γ 费米面，在20 K 的低温时有一个明显的能隙打开，随着温度的上升，能隙逐渐减小，并在50∼55 K 左右消失。而APRES 对于铁基超导体的测量通常表明，超导能隙会在超导转变温度附近关闭[110,113]，所以这也意味着单层FeSe 超导薄膜的Tc可能在(55±5) K 左右。并且这个结果在另一个独立的样品的测量中是可重复出的。图16(d) 中超导能隙随温度的变化关系也符合BCS 型的能隙温度变化关系。为了将这个结果和其他类型的FeSe 超导体做一个对比，作者找到(TI,Rb)xFe2−ySe2超导体在低温时的能隙大小约为9.7 meV[108]，而单层FeSe 在20 K 时的能隙宽度约15 meV，如果作者假设单层FeSe 也有着同(TI,Rb)xFe2−ySe2超导体一样的能隙大小与超导转变温度的比值，可以发现单层FeSe 薄膜的Tc为50 K，这个结果和单层FeSe 薄膜的ARPES 实验是符合的。

除了能对超导能隙进行温度依赖的测量，作者还可以对超导能隙进行动量依赖的测量。为了达到这个目的，在测量的时候就得对M 点的γ 费米面进行高分辨的费米面扫描（能量分辨率为4 meV）。图17 就是对γ 费米面附近在20 K 的温度下测量得到的光电子能谱的EDC，相应的对称化能量分布曲线在图17(b)中。为了避免偶然性，使实验结果更具有说服力，作者对两个不同的实验样品进行了独立的测量，而这两次测量的结果都一致表明超导能隙的各向同性。样品1给出的超导能隙大小为(13 ± 2) meV，而样品2 给出的超导能隙大小为(15 ± 2) meV。在实验中，作者注意到单层FeSe 的超导性对于其制备和退火过程很敏感。所以两个样品超导能隙的微小差别很可能是由于退火条件的微小不同从而使超导相也产生了微小的变化进而导致的。在这两个样品中，所有的能隙都处于打开状态。这是因为单层FeSe 薄膜严格的二维属性，这样就避免了体材料中费米面在三维状况下的复杂性，清晰地表明超导能隙中不存在节点。

综上所述，第一，对于当时最新发现的AxFe2−ySe2超导体而言，因为其中同时存在很多不同的相，所以不能辨别哪一个相处于超导相[108]，因而在超导相的确定这个问题上是有争议的。但单层FeSe 超导薄膜却能直接给出没有Fe 空位缺陷的FeSe 相是高温超导相。第二，在Γ 点附近完全缺失的费米面排除了在Γ 点费米面和M 点费米面之间的任何散射机制存在的可能性。这使得解释单层FeSe 薄膜的高温超导性相比于AxFe2−ySe2来说要更加直接简单一些，因为在AxFe2−ySe2中仍然存在Γ 点附近的电子型费米面。第三，因为其严格的二维属性，现在的观察就可以直接表明其超导能隙的各向同性与无节点性。但是如果想要在三维的材料中得出这样的结论，就必须沿kz方向对整个动量空间进行测量[118]。

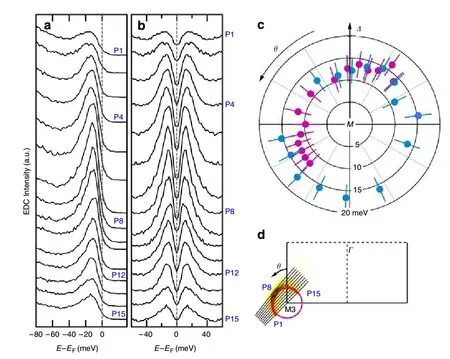
图17. 单层FeSe/SrTiO3 薄膜超导能隙的动量依赖测量。(a) 沿γ 费米面测量得到的EDC；(b) 对称化后的EDC；(c) 超导能隙的动量依赖关系；(d) 样品#1 在M3 点附近的费米面以及多个动量测量线在布里渊区中的位置。引自文献[20]

同时，对单层FeSe 超导薄膜的研究还对铁基超导的配对机制的研究也有着很大的推动。对于铁基超导来说，一般认为Fe 原子的五个3d 轨道一起形成多个费米面：Γ 点附近的空穴型费米面和M 点附近的电子型费米面[119]。并且Γ 点费米面和M 点费米面之间的散射被认为是电子配对和产生超导性的来源[119−125]。但是在单层FeSe 超导薄膜中完全不存在Γ 点的费米面，这完全否认了Γ 点和M 点的费米面之间的散射可能性。也因为缺失了Γ 点的费米面，如果讨论散射机制，则只能发生在M 点的费米面上，这就会产生预言的d 波超导能隙[119,126−128]。但是在一个给定的M 点附近的两个相位相反的费米面会促进能隙中出现节点[129]，而实验结果却并不符合这一构想[130]。而其他的一些物理图像，比如和局域铁磁矩[131−135]或者轨道涨落[136−137]之间的相互作用，需要被考虑进去，从而更好地理解单层FeSe 薄膜超导体产生高温超导的物理机制。

但仍然存在一些问题需要进一步探索。首先是单层FeSe 超导薄膜的STS 测量结果在±20.1 和±9.0 meV 处存在四个峰[11]，这说明其存在两个超导能隙的结构，但目前所进行的ARPES 实验没有能对这种双能隙结构进行重复。并且这种现象也不能利用在AxFe2−ySe2超导体中发现的多个能隙出现在不同的费米面上来进行解释，因为ARPES 实验给出的结果是单层FeSe 薄膜的各向同性的超导能隙以及在M 点附近只存在一个费米面。而扫描隧道也是一种局域探测，也不太可能因为那么小尺度上的不同相而导致这四个峰的出现。而另外一种可能就是单层FeSe 薄膜和FeSe/SrTiO3界面处都处于超导态并且有不同的超导能隙。但是作者观察到的费米面结构主体上是与能带计算得到的FeSe 费米面结构一致，并且也没有观测到界面处的二维电子气在Γ 点的电子型费米面。所以结果表明观测到的是单层FeSe 的超导性质。而FeSe和SrTiO3之间的晶格常数分别为3.76 ˚A 和3.905 ˚A，存在晶格失配。所以SrTiO3会对FeSe 层施加一个张力。因为FeSe 的超导性对压力的敏感性，所以这一个拉力在单层FeSe 产生高温超导上可能有着重要的作用。

单层FeSe 薄膜这种极其简单的电子结构，使得人们对这种材料高温超导的研究变得相对容易，而通过对这种材料高温超导的研究，反过来对推动铁基高温超导原理的研究具有非常重要的意义。

提高超导转变温度Tc是超导研究中的一个重要问题，这对于超导体的应用具有很强的现实意义，那么，是否能够将单层FeSe 薄膜材料的超导转变温度Tc进一步提高呢？

C. 单层FeSe/SrTiO3 薄膜材料的退火处理和Tc的提高

对于铜氧化物超导体，其在超导态的时候，调节超导转变温度Tc可以通过调节载流子浓度实现。在最初的时候，随着掺杂的增加，Tc也会不断提升，但当达到最佳掺杂的时候，Tc会达到最大值，之后又会随着掺杂的增加从而下降[138]。对于块体铁基超导体来说，也存在类似的现象，那么，是否可以通过调节单层FeSe 薄膜中的载流子浓度从而提升其超导转变温度呢？进一步了解这一系列的变化对于理解铁基超导体高温超导的起源有着重大意义。

在这里，作者使用真空原位退火的方法对载流子浓度进行有效调控。为了得到FeSe 薄膜的电子结构随退火的变化，ARPES 测量和退火连续交替进行。在退火完成后，将样品传入测量腔，在完成测量之后再传出到退火腔进行退火处理，在整个过程中样品均处于超高真空环境中，从而保持样品表面的清洁。

图18 是本次实验对单层FeSe 薄膜所用的退火温度及时间。条形图的颜色表示退火温度，而其高度代表时间，每一个阶段条形图的高度和颜色指目前的样品所经历的退火过程。以其中的第10 次退火为例，条形图代表样品在190◦C 经历2 小时的退火，之后又在250◦C 经历2 小时的退火。值得说明的一点是，在本次实验中使用了两个样品进行测量，这是因为随着退火的进行，薄膜的质量会逐渐变差，所以很难所使用一块样品完成全部的测量。为了展示出一个完整的退火变化过程，在实验中特意使用两块样品分别完成不同退火阶段的实验测量。

图19 是单层FeSe 超导薄膜在退火过程中费米面的变化，相应的能带结构展示在图20 中。同时，为了检查测量得到的光电子能谱是否来自衬底SrTiO3，所以作者准备了一块SrTiO3衬底，并将其进行和单层FeSe 薄膜相同的退火过程，结果显示，作者仔细的ARPES 实验发现没有来自衬底的能带结构贡献。

作者发现，随着退火，样品的载流子（电子）浓度逐渐增加，这可以从M 点电子型费米口袋面积的增大看出。但退火过程对电子掺杂产生影响的具体原因还有待进一步的研究。随着退火的进行，表面的Se 原子很容易被蒸发，而Se 空位缺陷会使得电子掺杂浓度上升，这一点在之前生长在石墨烯上的FeSe 的STM实验中是有发现的，但不能对单层FeSe 下这个结论。除了Se 的蒸发，还有可能是SrTiO3表面的氧原子蒸发导致电子掺杂浓度上升。而在退火过程中Fe 原子和Se 原子的重新排布也有可能会引起电子掺杂浓度的上升。为了确定退火过程中产生电子掺杂的具体原因，在后续的实验中作者还对双层和单层FeSe 薄膜进行了研究（详细内容见本文III.E 节）。与此同时，作者也对退火过程中能带的演化过程进行了详细的测量，如图20 所示。

图20. 单层FeSe/SrTiO3 薄膜在高对称方向的能带结构随退火的变化过程。这些图像是对原始数据沿能量方向做二次微分后得到的图像。(a)-(c) 分别为Γ、M2、M3 点处FeSe/SrTiO3 薄膜的能带结构随退火的变化；(d) 为N 相能带结构示意图；(e) 为S 相能带结构示意图；(f) 和(g) 为N 相和S 相中能带顶的位置随退火变化的示意图；(h) 为载流子浓度随退火的变化。引自文献[21]

接下来作者讨论退火（载流子浓度变化）对超导转变温度的优化。如图21 所示是单层FeSe 薄膜在不同阶段下（第10 步退火后）的超导能隙关闭温度依赖测量结果。为了更好观测到超导能隙，作者在图21(a)-(d) 中给出了在不同温度下测量得到的对称化EDC。利用对称化的EDC 曲线得到超导能隙的方法在铜基超导体的研究中使用了很长的时间，并且其结果和其他实验方法测量得到的一致。因此，利用对称化EDC 测量得到的能隙大小以及超导转变温度是可信的。图21 中(a)-(d) 中的提取的超导能隙大小分别展示在图21(e)-(h) 中。可以看到，超导能隙随着退火过程逐渐增大，从第10 步的大约10 meV 增加到了第15 步中的约19 meV，相应的能隙关闭温度也从第10 步的40 K 提升到了第15 步的65 K 左右。对于每一步的退火，其温度依赖得到的能隙都满足BCS 型能隙曲线。

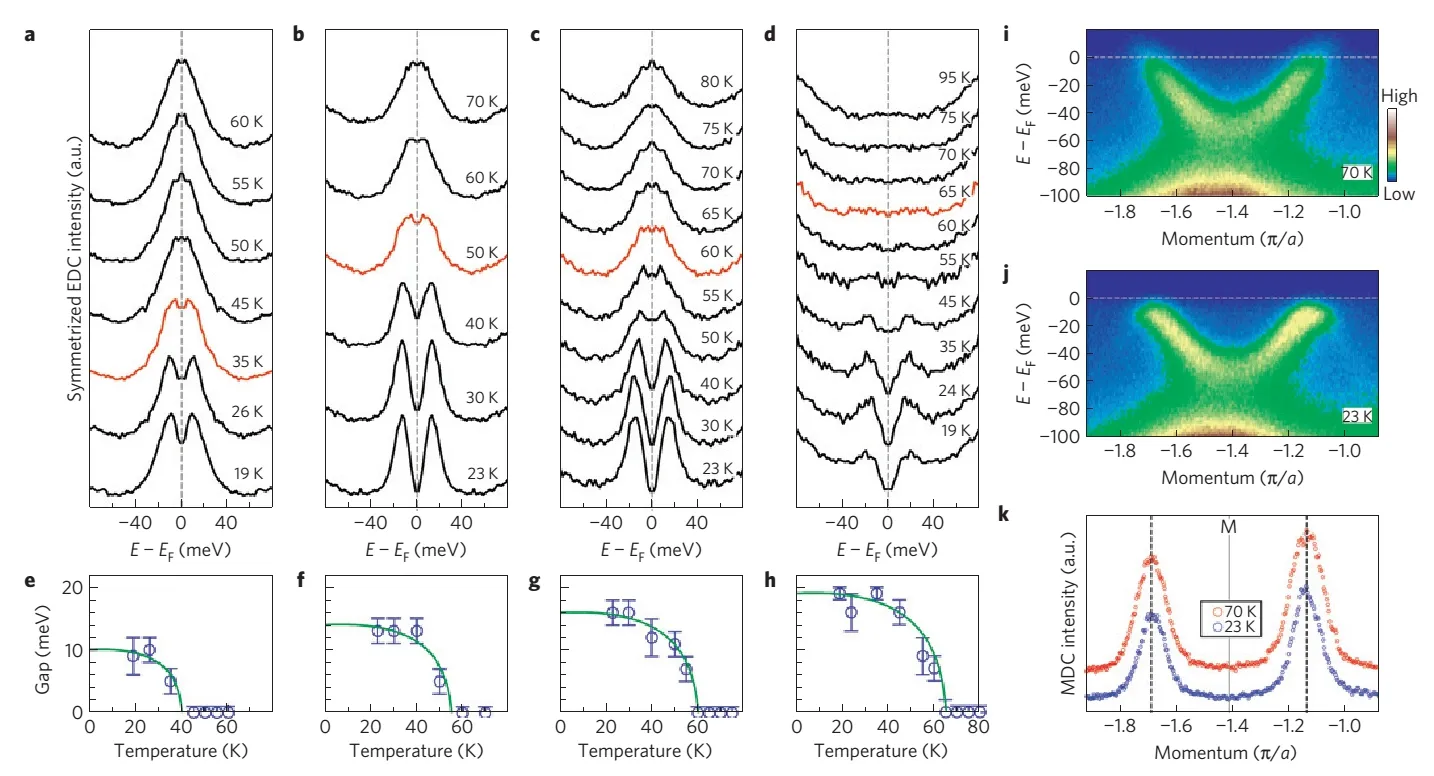
图21. 在不同退火条件下单层FeSe/SrTiO3 薄膜超导能隙的温度依赖关系。(a)-(d)为不同温度下KF 处对称的EDC；(e)-(f)为不同退火条件下超导能隙随温度的变化关系；(i) 和(j) 为70 K 和23 K 时M3 点的能带结构；(k) 为70 K 和23 K 时EF处的MDC。引自文献[21]

然而上述讨论中还有一个问题：为什么这个能隙是超导能隙而不是其他类型的能隙呢？为了探究这个能隙的本质，作者对能隙的动量依赖和温度依赖做了仔细的实验。作者对费米动量在转变温度下和上都进行了测量（图21(i)-(k)），发现费米动量位置并不随温度变化。到目前为止，超导能隙是唯一在整个布里渊区都打开，并且因为Bogoliubov 准粒子的原因形成了沿着费米面对称的能隙。这区别于自旋密度波和电荷密度波只在完美满足嵌套条件的部分费米面上打开能隙[139,140]，且费米动量通常会在超导转变温度上下发生变化。因此，作者的观测有力地表明之前测量到的能隙是超导能隙[98]。更进一步会发现，其对温度依赖得到的BCS 型的能隙表明这个能隙不太可能是赝能隙，就像在铜基超导里面发现的一样[141]。值得说的是，后来的电阻测量实验也直接证明了其超导性，所以这个能隙是超导能隙。

D. 单层FeSe/SrTiO3 薄膜从绝缘体到超导体转变的电子结构证据

对于铜氧化物超导而言，其具有电子强关联，并且母体为Mott 绝缘体，普遍认为其中的超导是随着对反铁磁Mott 绝缘体的掺杂而出现的。那么，这种铜氧化物超导中对Mott 绝缘体进行掺杂并出现超导的图像是否能适用于铁基超导呢？然而，铁基超导母体往往不是绝缘体，而具有的反铁磁坏金属特性。这使得人们讨论，铁基超导是更加倾向于巡游图像还是局域图像呢？一些理论计算表明，铁基超导的母体更加倾向于Mott 绝缘体[132,142,143]，人们也在尝试在理论上统一铜基和铁基超导[144]。但是，到目前为止，人们还没有发现在铁基超导体中存在绝缘体–超导体转变的结果。

在本次实验中，系统的ARPES 实验表明，通过对单层FeSe/SrTiO3薄膜中载流子浓度的调节，作者发现了铁基超导中的第一个绝缘体–超导体转变。在载流子浓度很低的时候，费米面附近的谱重被抑制，并且伴随着一个绝缘能隙的打开。当载流子浓度增加，谱重逐渐填进绝缘能隙，从而导致了能隙变小并伴随着在费米面附近的准粒子峰的出现。最终当载流子浓度达到一个合适的值时，绝缘能隙关闭，而超导能隙逐渐显现出来。在单层FeSe/SrTiO3薄膜中的这一个演化过程和在铜氧化物超导中观察到的绝缘体–超导体转变非常相似。这种相似为理解它们的超导机理有着重要的意义。同时，在单层FeSe/SrTiO3薄膜中发现的绝缘体–超导体转变也表明了降低维度在材料的物理性质和超导中的重要作用。

图22 是单层FeSe/SrTiO3薄膜的电子结构随掺杂浓度的演化过程（图22(a)-(g)）。测量是在20 K 左右沿着图22(O) 中M2 点上的白色动量线进行的。为了作比较，图22(h)-(n) 是La–Bi2201 系统沿着(0,0)−(π,π)节点方向得到的能带结构随载流子浓度的演化过程。对于La–Bi2201 系统而言，在掺杂浓度约为0.10的重度欠掺杂区域，也存在绝缘体–超导体转变。在这个掺杂浓度之下时，在节点区域存在一个能隙并且整个费米面都存在能隙[145]。从图22 中可以发现，在非常低的掺杂浓度的时候，单层FeSe/SrTiO3薄膜的电子型能带强度很弱（图22(a)）。随着掺杂浓度的增加，其谱重不断增强。这种演化和在La–Bi2201 系统中的发现很相似。

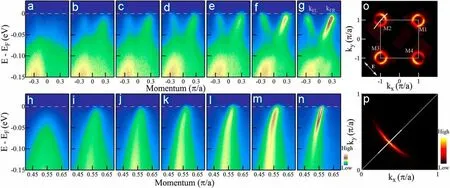
图22. 单层FeSe/SrTiO3 薄膜电子结构随掺杂的演化与La–Bi2201 的对比。(a)-(g) 载流子浓度分别为<0.073, 0.073, 0.076,0.087, 0.089, 0.098 和0.114 时的电子结构。测量时在20 K 左右沿着(o) 中在M2 点的动量线进行的。作为比较，(h)-(n)是La–Bi2201 系统在掺杂浓度分别为P = 0.03, 0.04, 0.055, 0.07, 0.08, 0.10, 0.16 时的能带演化。测量是在15 K 左右沿着(p) 中的节点动量线进行的。引自文献[22]

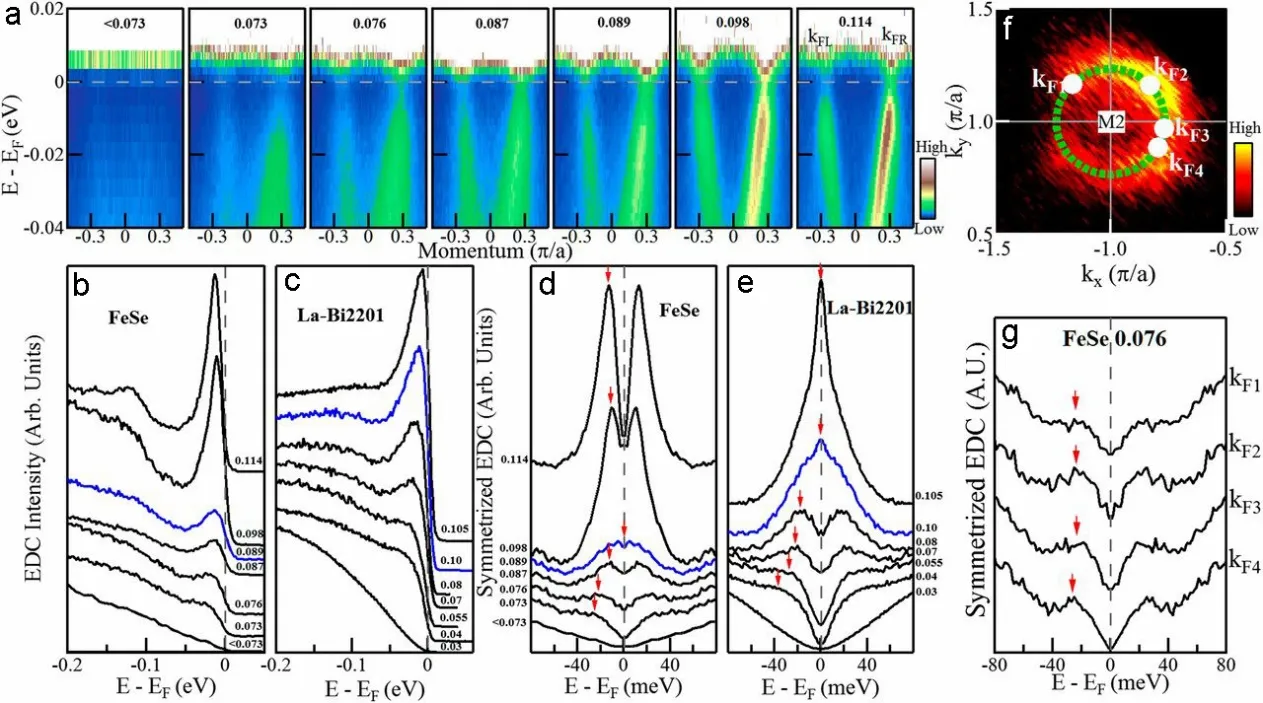
图23. 单层FeSe/SrTiO3 薄膜的光电子谱和能隙随着掺杂的演化以及作为对比的La–Bi2201 系统的测量数据。(a) 在载流子浓度分别为<0.073, 0.073, 0.076, 0.087, 0.089, 0.098 和0.114 时沿着图22 所示的动量方向得到的光电子能谱数据。为了看清打开的能隙，其费米–狄拉克分布函数已被移除。(b) 在a 中标记的KFR 的费米动量上的原始EDC（载流子浓度为0.114的样品）。对称化的EDC 展示在(d) 中。(c) La–Bi2201 沿着图14(p) 中节点方向的原始EDC。对称化的EDC 展示在(e)中。在掺杂浓度低于0.10 的时候，在节点方向存在能隙的打开；在高于0.10 的掺杂浓度时，样品成为超导并有一个d 波超导能隙。但是这个超导能隙在节点方向为0，所以在掺杂浓度为0.105 的时候没有观察到节点能隙。(f) 载流子浓度为0.076的FeSe 样品在M2 点的费米面。绿色虚线大致示意其费米面。(g) 沿着费米面在不同的动量处测量得到的对称化EDC。红色箭头是能隙的位置。引自文献[22]

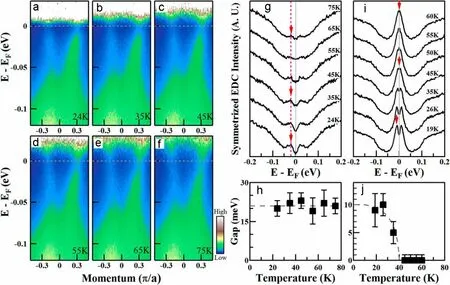
图24. 单层FeSe/SrTiO3 薄膜中两个能隙不同的温度依赖关系。(a)-(f) 载流子浓度为0.076 的FeSe 样品分别在24, 35, 45,55, 65 和75 K 下沿着图22(o) 中的动量方向在M2 点测量得到的光电子能谱数据。同样也做了对费米面附近的费米–狄拉克分布函数的移除。(g) 载流子浓度为0.076 的FeSe 样品在不同温度下在费米动量KF 处测量得到的对称化EDC。红色箭头代表能隙所在的位置。对应的能隙大小随温度的变化展示在图(h) 中，在测量的温度范围内几乎不随温度变化。(i)载流子浓度为0.098 的FeSe 样品在不同温度下在费米动量KF 处测量得到的对称化EDC。对应的能隙大小随温度的变化展示在图(j)中，符合BCS 型的能隙行为。引自文献[22]

图23(b) 是单层FeSe/SrTiO3薄膜M2 点的电子型能带KF（图23(a)）处的EDC，测量温度约为20 K。载流子浓度低于0.073 时，对应的EDC 在费米面附近的谱重很低。当载流子浓度上升，首先在费米面附近出现一个准粒子峰，并且逐渐增强，在载流子浓度为0.114 时变成一个尖锐的峰。在图23(a) 中，为了更好的观察可能存在的能隙打开，作者在数据中去除了费米–狄拉克分布函数的影响。可以看到，在低载流子浓度时被抑制的能谱强度表明存在一个打开的能隙。随着载流子浓度的上升，这种抑制减弱，在掺杂浓度为0.089 的时候，能隙关闭。但是，载流子浓度的进一步提高使得在费米面附近的能谱强度重新减弱，意味着一个新的能隙打开。为了定量分析能隙大小的变化，作者将原始的EDC 对称化处理得到对称EDC（图23(d)）。从图23(d) 中可以清楚地看到，当载流子浓度较低的时候，有能隙打开，表现为对称化EDC 在费米能级的一个谷。当载流子浓度增加，能隙大小逐渐减小，在掺杂浓度为0.089 时能隙关闭。在载流子浓度继续增加，到了0.098 和0.0114的时候，能隙又再次打开。作为对比的La–Bi2201的EDC 随掺杂浓度的变化和相应的对称化EDC 分别展示在图23(c) 和(e) 中。单层FeSe/SrTiO3薄膜随载流子浓度的演化表现出了同La–Bi2201 系统[145]及其他一些铜氧化物超导系统[146]相似的行为。在单层FeSe/SrTiO3薄膜中打开了两个能隙，一个是载流子浓度低于0.089 时存在，另一个是在高于0.089 时产生，他们表现出了对温度不同的依赖关系（图24）。高载流子浓度的能隙表现出了对温度的强烈依赖关系，在约40 K 时会关闭（图24(i)，x = 0.098）。并且这个能隙的大小随温度的变化关系符合BCS 型能隙温度变化关系。结合在EDC 中发现的尖锐的相干峰（图24(i)）以及之前作者发现的粒子–空穴对称性[20,21,147]，都强烈地表明这个能隙是超导能隙。而在低载流子浓度时的能隙在以下几个方面表现得不同：

1. 在所有温度下测量得到的EDC 峰都非常宽，没有相干峰那样尖锐。

2. 能隙的大小几乎不随温度变化。图24(a)-(f)是对载流子浓度为0.076 的样品在M2 点沿着图22(o)中的方向测量得到的能带结构随温度的变化关系。为了看清楚费米面以上的能带，作者也将费米–狄拉克分布函数去除。

3. 这个能隙很大，在载流子浓度低于0.073 的时候都能达到50 meV，这比在单层FeSe/SrTiO3薄膜中发现的最大超导能隙还大很多[16,100,146]。

这些不同的行为都表明在低载流子浓度时的能隙和超导能隙是不同的。在另一方面，这个能隙宽的EDC 峰，对温度没有明显的依赖关系，以及和超导能隙相比的大尺寸，都和在绝缘重度欠掺杂的铜氧化物的能隙相似。因此，作者认为这个能隙更加符合绝缘能隙。作者也对这个能隙的动量依赖做了测量。在图23(g) 中，在实验误差允许范围内，能隙大小沿着费米面基本不变，这也符合绝缘能隙的各向同性。

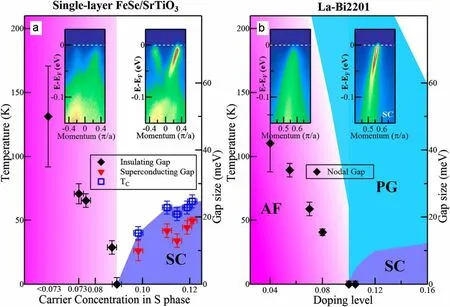
图25. 单层FeSe/SrTiO3 薄膜和La–Bi2201 的相图示意。引自文献[22]

上述的结果清楚地表明，在低载流子浓度的时候，单层FeSe/SrTiO3薄膜表现出绝缘行为。并且能隙大小随着载流子浓度的上升逐渐减小直到在x =0.089 的时候消失。在比这个载流子浓度更高的时候，超导开始出现。上述过程的演化进程和在超导区域更高载流子浓度时的能隙变化示意图展示在图25(a)中。这就导致了在0.089 的临界载流子浓度处出现绝缘体–超导体转变。同样，为了做对比，作者也给出了La–Bi2201 系统在掺杂浓度为0.10 处绝缘体–超导体转变的相图（图25(b)）。很有趣的是单层FeSe/SrTiO3薄膜和La–Bi2201 系统在能带结构、EDC、能隙的打开以及相图上都有很多相似之处。当然这两个系统也存在一些不同之处。La–Bi2201 系统的母体材料是反铁磁绝缘体，随着掺杂浓度的增加，节点能隙在0.10时减弱到0，同时伴随着三维反铁磁现象的消失。在单层FeSe/SrTiO3薄膜中，是否具有磁性相仍然不太清楚。另一个不同在于单层FeSe/SrTiO3薄膜是严格的二维系统，在超导态的时候也仍然为严格的二维状态；而La–Bi2201 系统是准二维系统，在超导态的时候成为了三维状态。

在2014 年，斯坦福大学的沈志勋组通过高分辨的ARPES 实验，发现单层FeSe/SrTiO3薄膜的电子结构存在一些特殊的能带结构，通过仔细的分析发现，这些特殊的能带起源于衬底的声子和单层FeSe 中的电子之间的耦合。通过将单层、双层以及30 层FeSe薄膜进行比较，发现界面处的电声耦合对库伯对的形成有增强的作用[148]。并且，理论计算结果也表明，界面处的电声耦合会提高其超导转变温度[148]。

至此，可以得出一个结论：单层FeSe 薄膜极高的超导转变温度Tc形成的原因可能来源于电子的强关联效应以及衬底与材料间形成的电声耦合作用。

E. 单层和双层FeSe 薄膜在电子结构以及超导性上的差异

如上所述，单层FeSe 薄膜通过掺杂能达到很高的超导转变温度，但STM 的研究在双层FeSe 薄膜中却似乎没有发现这种现象。为了回答这个问题，同时也为了更进一步探索其高温超导产生的物理机制，作者对生长在SrTiO3衬底上的单层FeSe 薄膜和双层FeSe薄膜进行了系统的退火处理和ARPES 实验进行研究和比较。

图26. 相同条件退火后单层、双层FeSe/SrTiO3 薄膜电子结构的不同。(a)、(e) 是退火后的单层、双层FeSe/SrTiO3 薄膜的费米面；(b)-d、(f)-(h) 分别是单层、双层FeSe/SrTiO3 薄膜在Γ、M2、M3 点切得的能带结构。引自文献[23]

为了比较研究双层与单层FeSe/SrTiO3薄膜，作者把当刚制备好的单层FeSe/SrTiO3薄膜和双层FeSe/SrTiO3薄膜在相同的条件下进行退火处理，然后运用ARPES 对其电子结构进行测量。单层FeSe/SrTiO3薄膜在该退火条件下，其费米面结构表现为M 点附近存在电子型的费米面，而且在Γ 点附近没有费米面存在的迹象（图26(a)）；其能带结构表现为在Γ 点存在一条顶部在费米面以下80 meV 的空穴型能带（图26(b)），在M 点附近存在一条穿过费米面的电子型能带（图26(c)、(d)）。对于这个特定的退火样品，其超导能隙在40 K 左右关闭[21]。但是，在相同的退火条件下，双层FeSe/SrTiO3薄膜的费米面（图26(e)）和能带结构（图26(f)-(h)）却与单层薄膜存在显著差异。我们注意到，在之前的STM对同一块样品的测量结果中，单层FeSe/SrTiO3薄膜区域在20.1 meV 的位置处表现出了相干峰，双层FeSe/SrTiO3薄膜区域表现出了半导/绝缘行为[100]。现在的ARPES 实验结果和之前的STM实验结果都表明，即使双层FeSe/SrTiO3薄膜和单层FeSe/SrTiO3薄膜在相同的条件下退火，仍然表现出不同的行为[100]。

既然单层FeSe/SrTiO3薄膜可以通过退火调节载流子浓度，发生从绝缘体到超导体的转变[22]，并在超导相中进一步提高超导转变温度[21]，那么是否可以通过退火调节载流子浓度使双层FeSe/SrTiO3薄膜也超导呢？通常退火效果可以通过增加退火时间和升高退火温度从而得到提升。作者对两个样品分别使用了这两种方法进行退火的提升，结果展示在图27 和图28 中。图27(a) 是双层FeSe/SrTiO3薄膜在350◦C的固定温度下增加退火时间得到的费米面演化图。图27(b)-(d) 是在三个典型点所切得的能带结构演化结果。作者发现，当退火时间足够长时，费米面和能带结构表现出与单层薄膜退火后其类似的结果。同时发现一个大小约为18 meV 的能隙，并且该能隙大小几乎不随温度变化，直到70 K 时依然存在。这与单层FeSe/SrTiO3薄膜在低掺杂状态中发现的绝缘能隙很类似。

图28 是双层FeSe/SrTiO3薄膜（样品2）逐渐升高退火温度得到的费米面和能带结构演化。作者发现，在使用的最高温度(535◦C) 退火后，运用ARPES 测量时可以在低温下看到明显的相干峰和明显的能隙，并且能隙的大小在13.5 meV 左右，这个能隙最终会在55K 附近关闭。这个观测结果和单层FeSe/SrTiO3薄膜中的超导能隙结果相似，这表明在序列6 时的样品是超导的。

图27. 双层FeSe/SrTiO3 薄膜（1 号样品）在350◦C 下不同退火时间的电子结构。退火序列1–6 分别对应累计退火时间为15, 30.5, 46.5, 66.5, 87.5, 92.5 小时。(a) 费米面随退火时间的演化。(b)-(d) 沿着过Γ(b)、M2(c)、M3(d) 点的动量线（如图26 所示）测量的能带结构随退火时间的演化。(e) 序列6 样品在沿着过M2 点的动量线测量得到的原始能带结构图，左、右分别为23 K、70 K 下的结果。(f) 序列6 样品在不同温度下测量得到的对称化EDC 曲线。引自文献[23]

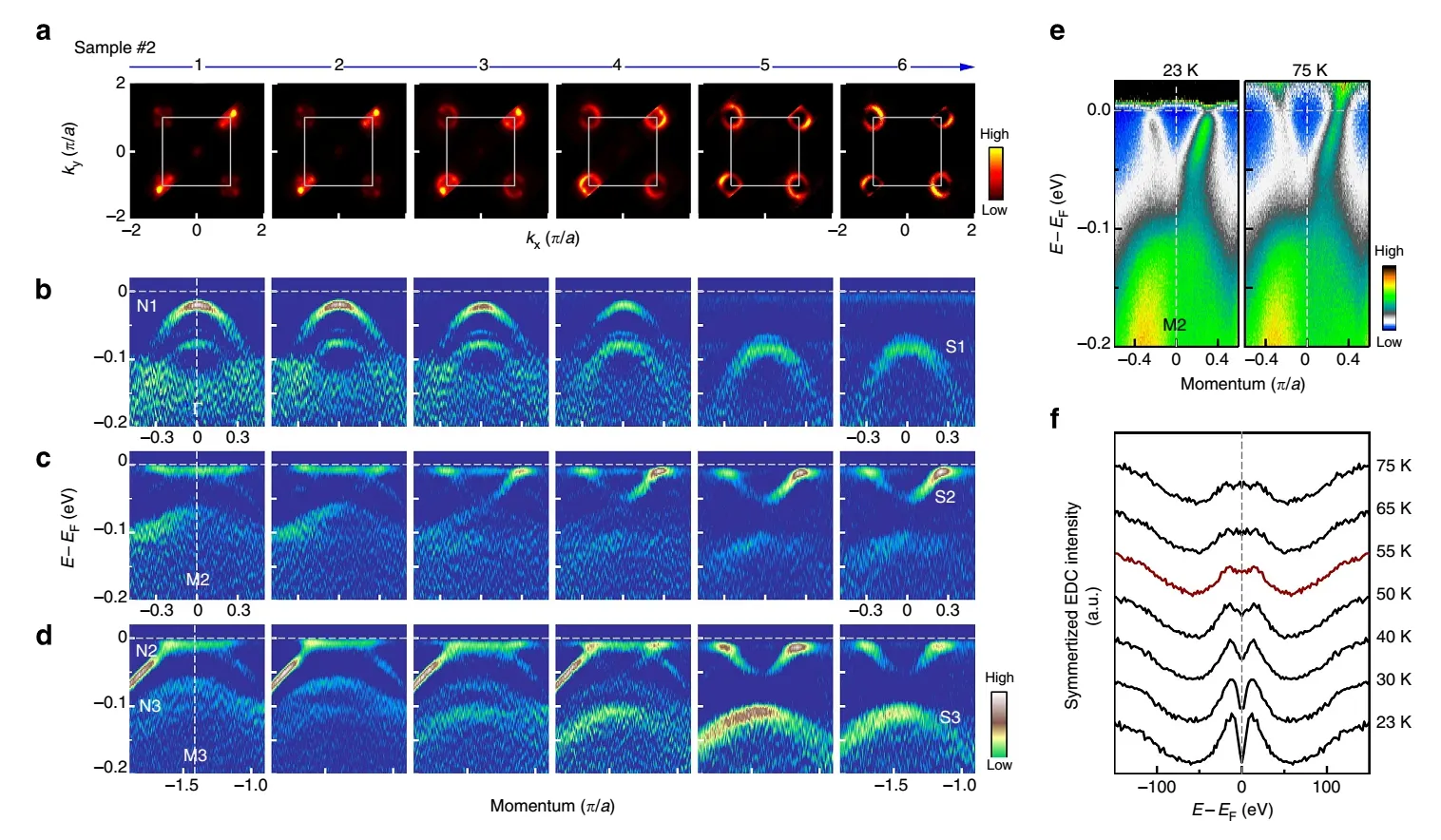
图 28. 双层 FeSe/SrTiO3 薄膜（2 号样品）在不同退火温度的电子结构。退火序列 1–4 分别对应退火温度为350◦C、450◦C、500◦C 和535◦C，序列5、6 是在535◦C下增长退火时间。(a) 费米面随退火的演化。(b)-(d) 沿着过Γ(b)、M2(c)、M3(d) 点的动量线（如图28 所示）测量的能带结构随退火的演化。(e) 序列6 样品在沿着过M2 点的动量线测量得到的原始能带结构图，左、右分别为23 K、75 K 下的结果。（f）序列6 样品在不同温度下测量得到的对称化EDC曲线。引自文献[23]

由上述结果可以看出，在对双层FeSe/SrTiO3薄膜的退火中，保持350◦C 并延长退火时间可以得到类似的绝缘能隙但不能产生超导；但把退火温度提高到535◦C 时似乎可以出现超导。然而作者发现双层薄膜退火过程远比单层薄膜复杂，因为在退火过程中还存在FeSe 的蒸发。对于单层FeSe/SrTiO3薄膜，因为衬底SrTiO3不会贡献明显的信号，即使部分FeSe 蒸发了，作者也总能探测到单层薄膜的电子结构。但是双层FeSe/SrTiO3薄膜便完全不同，在退火过程中，有可能顶层的FeSe 蒸发使得一些区域成为单层薄膜。为了验证这一可能性，作者使用了STM 对退火前后的FeSe/SrTiO3薄膜进行了观察。在图31a,b 中，在退火温度相对较低（450◦C）时退火15h，双层FeSe区域在退火前后保持一致。但从图31c,d 中可以看到，当退火温度增加到500◦C 时，仅仅3h 的退火，原来三层FeSe 的区域已经明显减小，并且在原始样品中不存在的单层区域也显现出来了。这表明在高温达到500◦C 或者更高的温度时，FeSe 在退火过程中的蒸发变得显著。

根据STM 的实验结果，我们可以更好地理解ARPES 测量中两种不同退火方式（延长时间或升高温度）得到的不同结果。在第一种情况下，双层FeSe/SrTiO3薄膜（样品1）的退火温度为350◦C。因为这个温度比450◦C 低很多，因此能够极大程度减少FeSe 的蒸发从而保证双层FeSe/SrTiO3薄膜在退火过程中的完整性。有人或许会问到，尽管退火温度很低，但由于长时间的退火，一些区域或许仍然可能变成单层FeSe/SrTiO3薄膜，而不能表现出双层FeSe/SrTiO3薄膜的特性。尽管作者不能完全排除这一可能性，但实验结果并不支持这一可能性。因为如果存在单层FeSe/SrTiO3薄膜，根据作者对单层FeSe/SrTiO3薄膜的退火实验结果来看[21,22]，这些单层FeSe/SrTiO3薄膜的区域早已在作者使用的退火条件下变成超导态。这和作者在双层薄膜中观察到的绝缘能隙不符合。在另一方面，尽管作者在2 号样品的双层FeSe/SrTiO3薄膜中观察到了超导能隙，但结合STM 结果，这极大可能来自在退火过程中蒸发掉顶层FeSe 从而形成单层FeSe 区域，使得作者观测到单层FeSe/SrTiO3薄膜的行为。

上述的结果清晰表明对双层FeSe/SrTiO3薄膜的掺杂比对单层FeSe/SrTiO3薄膜的掺杂更为困难。

对双层 FeSe/SrTiO3薄膜退火的研究为理解FeSe/SrTiO3薄膜中超导的起源也提供了重要的信息。FeSe/SrTiO3薄膜的超导起源从哪里来一直是一个重要的问题。对于这个问题，主要有三种设想：(i)独立的FeSe 层；(ii)SrTiO3衬底；(iii)SrTiO3衬底和FeSe 之间的界面。而双层FeSe/SrTiO3薄膜和单层FeSe/SrTiO3薄膜在电子结构上的不同就表明超导不可能单独来自于FeSe 层。如果超导只来源于FeSe 层，那么作者会得到一个结论，双层FeSe/SrTiO3薄膜顶部的FeSe 层的行为应该和单层FeSe/SrTiO3薄膜的FeSe 层的行为一致，但对单层和双层FeSe/SrTiO3薄膜在相同条件下退火的实验结果并不支持这一结论。同时，在石墨烯上生长的FeSe薄膜和在SrTiO3衬底上生长的FeSe 薄膜也表现出了显著的不同行为。联系这两个实验结果，得出的结论是界面对FeSe/SrTiO3薄膜超导的提升有着重要的作用。

图 29. FeSe/SrTiO3 薄膜在不同退火条件下退火前后在 STM 下的形貌。1UC 代表单层区域，2UC 代表双层区域，3UC 代表三层区域。(a) 刚生长好的单层为主的FeSe/SrTiO3 薄膜的形貌。(b) 在450◦C 下退火15 h的单层为主的FeSe/SrTiO3 薄膜的形貌。(c) 刚生长好的双层为主的FeSe/SrTiO3 薄膜的形貌。(d) 双层为主的FeSe/SrTiO3 薄膜在500◦C 下退火3 h 后的形貌。引自文献[23]

同时，目前对单层和双层FeSe/SrTiO3薄膜的研究清楚地表明了载流子浓度的提高在FeSe/SrTiO3薄膜超导性产生中的重要作用。因为只有在对界面处的掺杂达到一定程度的时候超导才会产生。而单层和双层FeSe/SrTiO3薄膜表现出的不同行为也为FeSe/SrTiO3薄膜中掺杂的机理提供了更进一步的信息。FeSe/SrTiO3薄膜在真空退火过程中产生载流子掺杂有两种可能的方式。一是Se 的蒸发导致在FeSe薄膜上产生Se 空位。另一个方式是在SrTiO3的表面附近产生的O 空位[20,21,147]。STM 对真空退火的单层FeSe/SrTiO3薄膜的实验表明[148]，在刚制备好的FeSe 薄膜上存在吸附原子，并且样品是绝缘的。在最初的退火过程中，这些多余的吸附原子逐渐被清除，而更进一步的退火导致了Se 空位的形成。退火过程对于样品从绝缘态转变到超导体的提升和ARPES实验观测到的结果也是一致的[17]。同理，如果掺杂过程只涉及到FeSe 层，再考虑到顶层和底层FeSe 在退火过程中相互作用较弱，作者也能得到一个结论，那就是单层和双层FeSe/SrTiO3薄膜在相同的退火条件下应该表现出相似的掺杂行为。这和实验观测的结果不一致（图28）。上述结果就清楚地说明掺杂过程不仅仅只单独来源于FeSe 层。而理论计算表明，Se 空位表现出空穴掺杂行为而不是电子掺杂行为。这更加表明SrTiO3衬底和FeSe/SrTiO3界面在掺杂过程中的重要作用。

正是因为对双层FeSe 薄膜进行掺杂十分困难，所以，双层FeSe 薄膜才表现出同单层FeSe 薄膜迥然不同的性质。要想在双层FeSe 薄膜中实现超导并提高超导转变温度，就需要进一步的研究去突破对双层FeSe薄膜进行掺杂的困难。

F. FeSe/SrTiO3 薄膜超导性质总结

利用ARPES 实验手段，作者直接看到了生长在SrTiO3衬底上的单层FeSe 薄膜简单而又特殊的电子结构。这种极其简单的电子结构能够帮助人们更加方便地分析其产生高温超导的机理，给高温超导机理的研究带来了极大的便利。同时，通过一个简单的退火过程便可以对这种材料进行掺杂。通过优化退火条件，实现了一个最佳载流子浓度，可以使得该超导体在这种载流子浓度下具有最高的超导能隙关闭温度，约为65 K。同时，作者发现该超导材料存在一个随着载流子浓度变化而发生的绝缘体到超导体转变，表明电子关联对该系统实现高温超导起着非常重要的作用。而作者对单层和双层FeSe 薄膜的研究与对比也进一步表明载流子浓度的提高在该系统中实现高温超导这一特殊的物理性质上的重要作用。

IV. 总结与展望

高温超导体及其机理的探索是凝聚态物理研究中的一个核心问题。本文综述了通过电子结构探索高温超导机理的一系列研究。主要从铜氧化物高温超导体及铁基超导体两个方面进行了介绍。在铜氧化物超导体部分主要介绍在Bi2Sr2CaCu2O8+δ材料中对电子–玻色子耦合及可能造成对称性破缺的电子序进行的研究；以及在YBa2Cu3O7−x/La0.7Ca0.3MnO3异质结中对三维准长程电子序的研究。在铁基超导体部分，主要介绍了对SrTiO3衬底上FeSe 薄膜的研究，揭示了其超导样品的电子结构；通过退火优化载流子浓度提高了超导能隙关闭温度；发现了随着载流子浓度变化的绝缘体到超导体转变的电子结构证据；通过对比研究理解了单层FeSe 薄膜和双层FeSe 薄膜的差异。然而，在对高温超导机理的探索中还存在非常多的重要问题亟待解决。我们相信对材料电子结构的研究将在这一探索过程中继续扮演非常重要的作用。