对数域梯度与改进Sobel算子相结合的边缘检测
2019-05-14任克强
任克强,张 镕
(江西理工大学 信息工程学院,江西 赣州341000)
1 引 言
边缘是模式识别中的重要的低层次特征信息,它是基于局部特征识别的重要依据。边缘信息对光照非常敏感,尤其当物体表面被阴影遮挡或光照角度变化时,不容易检测到完整的边缘信息,会造成严重的识别错误。因此解决好光照给边缘检测带来的问题,将会给社会生产、交通以及医学影像等领域带来重大意义[1-3]。
目前,常用的边缘检测算法有很多,传统的边缘检测算法包括Roberts算子、Canny算子以及Sobel算子等[4-6]。随着数学理论及技术的不断发展,涌现了许多新的检测算法,如基于小波变换、数学形态学、神经网络以及自适应阈值选取的边缘检测算法等。近年来,研究人员开始对光照问题的数字图像处理有了密切的关注[7-9],为解决光照不均的图像边缘检测问题提供了不少新的思路。文献[10]针对文本图像在二值化时,光照不均导致文本图像OCR识别率降低的问题,提出采用改进Roberts算子和分块动态双阈值相结合来削弱光照不均的影响;该方法在处理复杂文本时效果也很显著,但是存在复杂度较高的不足。文献[11]为了解决光照不均给准确测量微米尺度条纹间距带来的问题,先采用Retinex方法对原图像进行增强,然后使用Ostu最佳阈值对图像进行二次分割,克服了条纹边缘存在凹陷的困难,使得光学显微线条纹图像中心线能够准确提取;但该方法在进行阈值分割时存在较大的噪声,处理时间也比较长。文献[12]提出一种IKDSIFT(Improve keypoint detection algorithm based-on SIFT)算法,它是针对非均匀光照下基于对象识别的关键点检测算法,使用传统SIFT方法、形态学操作以及Top-Hat过滤等方法实现预处理,然后比较数据集的关键点速率,检测出一些峰值确定最佳阈值;该算法在处理不均匀图像的检测的效果比较显著,但是过程太过繁琐,效率较低。
针对上述方法处理剧烈光照变化导致的图像不均匀光照现象所存在的不足,本文提出一种基于对数域梯度与改进Sobel算子的边缘检测方法,通过在对数域建立梯度场来消除光照影响,再结合改进的Sobel算子以及通过Bernsen算法确定阈值进行边缘检测,以提升边缘检测的效果。
2 本文算法
2.1 对数域梯度预处理
光照条件的变化会对图像像素灰度分布产生显著的影响。由于光源发出光照射到物体,一部分光会经物体表面反射,一部分光会穿透物体,还有一部分会被物体吸收形成热能,因此只有反射光和透射光能刺激人眼产生视觉效果。图像亮度一般用图像辐照度来描述,辐照度对应物体对光的表面的反射,所以物体的图像亮度有两个因素影响,一个是入射光照射,其次是物体表面反射光照射。入射光照射取决于物体相对于光源分布,而物体表面反射光取决于物体的表面光学特性。
一幅二维数字图像可以用函数f(x,y)表示,用i(x,y)表示入射光量,用r(x,y)表示反射光量,可以表示为:
f(x,y)=i(x,y)×r(x,y) (1) 由于反射光取决于物体表面的光学特性,可以认定是图像的光照不变特征。无论光照条件如何,一般可以认为i(x,y)为图像低频部分,反射系数r(x,y)包含物体的各种细节可以认为图像高频部分。如果可将两者分开,然后削弱低频部分,增强高频部分,就能达到对光照不均的补偿目的。 对图像进行边缘检测,梯度信息受不均匀光照影响较大。为克服光照不均的影响,先将图像变换到对数域(仅对非零灰度值的像素变换到对数域,为零灰度值的像素直接取对应位置梯度取代),再采用梯度计算。幅度公式和梯度方向公式分别表示为: (2) (3) 假设i(x,y)分量是缓慢变化的,即i(x+1,y)≈i(x,y),i(x,y+1)≈i(x,y)。在此基础上可以证明对数域梯度变换只与反射分量r(x,y)有关,从而完成上述分离两分量,并削弱低频成分的目的。证明如下: (4) 同理可证: (5) 由式(4)、(5)的证明,可知图像边缘的对数域梯度的变化,近似反映为反射分量的变化,而与入射分量无关,所以对数域梯度场对光照具有不变性。最后对式(2)~(5)进行整合,可以将对数域梯度幅值和方向表示为: (6) (7) Sobel算子作为基于模板检测的一阶导数算子,在使用小模板时,能够获得较高质量的边缘像素集合。Sobel算子含有包括横向和纵向2个方向的3×3模板,在进行图像处理过程中,图像的每个点与两个方向的模板进行领域卷积,从而达到检测出水平和垂直边缘的目的,卷积运算表示为: (8) (9) 式中:A代表原始图像,Lx、Ly分别代表横向与纵向边缘检测图像灰度值,假设图像函数为f(x,y),则具体计算如式(10)、(11)所示。 将Lx、Ly进行合成梯度,梯度幅值与梯度 Lx=[f(x-1,y+1)+2f(x,y+1)+f(x+1,y+1)]- (10) Ly=[f(x+1,y+1)+2f(x+1,y)+f(x+1,y-1)]- (11) 方向角分别表示为: (12) θ(x,y)=arctan(Ly/Lx). (13) 考虑到梯度方向具有对称性,经典的sobel算子2个梯度模板能构成4个方向。为了同时能保证灰度图像的检测效果与效率,在水平梯度和垂直梯度的基础上,改进的Sobel算子另外增加了45°和135°方向的梯度计算,这样在进行检测时能达到8个方向,能有效提高检测效果。增加的梯度模板如图1所示。 图1 Sobel算子模板Fig.1 Sobel operator template 图像函数f(x,y)的3×3窗口: (14) 将Sobel算子0°、45°、90°和135°模板分别与f(x,y)卷积: (15) 梯度幅值用无穷范数表示为: (16) 经典Sobel算子是在卷积得到梯度幅值后,通过选取人工设定的阈值进行边缘提取,这样检测到的边缘效果较差。Bernsen算法作为一种局部二值化算法是将图像分割成块,然后分别计算阈值,通过比较选出最佳阈值。一般算法通常会忽略扫描框对周边像素的阈值选取,从而造成边缘断点或缺失,因此该方法可以抑制不均匀光照给图像带来的影响。 设定当前像素为Y(i,j),以Y(i,j)为中心做一个边长为2w+1的(2w+1)×(2w+1)窗口,w为窗口宽度参数,然后计算每个窗口的阈值TY(x,y): (17) 原始Bernsen算法得出来的阈值TY(i,j),若经强制处理则会无法避免噪声点,在细节上会变得极其敏感,故结合高斯滤波进行改进得出新的阈值TG(i,j),然后将TY(i,j)与TG(i,j)进行线性组合,通过调节线性参数a来确定最适阈值T(i,j)。 经高斯滤波后的Bernsen算法阈值TG(i,j): (18) 由于得出来的阈值容易产生伪影现象,故在线性组合确定最佳阈值之前,先对TY(i,j)与TG(i,j)进行平滑处理: (19) (20) 线性组合确定最佳阈值: (21) (22) (23) (24) 式中,0 通过以上步骤得到最适阈值T(i,j),然后与中心点像素Y(i,j)进行比较,如果比中心点像素大阈值取0,为背景像素;反之取1,为目标像素。进行比较的式子如下: (25) 经过与3×3窗口的9个像素比较后可以得到最大值与最小值,然后将两个最值的均值同中心像素值作比较,最后判断得出二值化结果并输出。 为了测试算法的边缘检测性能,选取像素为903×600低、中、高3组照度下的office_1、office_2、office_3灰度图像,对经典的Log算法、Laplacian算法、文献[12]算法以及本文算法进行比较实验。实验硬件平台:Intel(R)Core(TM)i5-4210M CPU @ 2.60GHz,8G内存;实验软件平台:Windows10 64位操作系统,MatlabR2017a。 该实验针对3组照度不同的原始图像进行对数域梯度预处理。由于office图像里面的内容元素比较丰富,在不同强度的光线照射下呈现的阴影程度具有区分度,因此很适合做不均匀光照的边缘检测对比实验。其中,图2(a)、图2(b)和图2(c)分别为低、中、高照度的office图像,预处理结果为图2(d)、图2(e)和图2(f)。 图2 对数域预处理前后的office图像对比Fig.2 Office images before and after logarithmic domain pre-processed 从图2可以看出,经过对数域梯度预处理,不同照度下的office图像都提升了亮度。其中低照度的图2(a)处理效果最好,相较于中、高照度的图2(b)和图2(c),处理后的图2(d)细节最为清楚。这主要是因为图像转换至对数域,在对数域求得图像梯度后,压缩了图像动态范围,增强了阴影处的信息,使得梯度均匀化,提高了对比度,而且越暗的地方,表现的效果越好。 为进一步展现对数域梯度预处理后的图像边缘检测效果,用经典Sobel算子对图2所有图像进行边缘检测。如图3所示,经过预处理后的Sobel边缘检测图像图3(d)、图3(e)和图3(f)相较于原始图像图3(a)、图3(b)、图3(c)边缘更加丰富、细腻;而且,低照度的office_1图像经对数域梯度预处理后的边缘检测效果尤为突出,中、高照度的office图像边缘检测效果依次减弱;由此可以说明经过对数域梯度预处理,能明显改善光照不均给图像边缘带来的识别不清影响,能够较完整的呈现图像边缘。 图3 对数域预处理前后的边缘检测效果Fig.3 Edge detection effect before and after logarithmic domain preprocessing 图4为经典Laplacian算子、Log算子、文献[12]算法以及本文算法分别对office_1、office_2、office_3灰度图像进行的边缘检测结果。用不同算法处理同一种照度下的office图像,低照度下的office_1图像边缘普遍都比office_2图像与office_3图像要好;在4种算法中,文献[12]算法和本文算法要比经典Laplacian算子与Log算子要好。经典算法和文献[12]算法在阈值选取上缺乏自适应性,因此会导致检测的图像出现部分断点,严重的地方会使图像边缘看上去不连续。本文算法增加45°和135°检测方向,使得检测范围更加全面,再结合线性组合的Bernsen算法阈值,增加了自适应性,使检测效果更加出色。为了进一步比较4种算法对3组图像的检测效果,利用峰值信噪比(peak signal to noise ratio,PSNR)来对实验结果图像进行定量评价,如表1所示。 表1 4种算法的PSNR值比较Tab.1 Comparison of PSNR values between four algorithms dB 从表1的结果可以看出,同等情况下,本文算法与文献[12]都优于经典Laplacian和Log边缘检测算子,本文算法又要比文献[12]效果要好;其中,本文算法相较于文献[12]低、中、高照度下的office_1、office_2、office_3图像,分别高出0.958 9,0.723 4,0.521 5 dB,说明本文算法在光照不均的情况下效果最好。 图4 本文算法与经典算法及文献[12]的比较Fig.4 Comparison of the algorithm in this paper with classical algorithms and Ref. [12] 当图像受到不均匀的光照进行照射时,很难识别其边缘,本文提出一种对数域梯度与改进Sobel算子相结合的方法来检测光照不均图像的边缘。为克服光照不均对图像边缘检测的影响,先将图像变换到对数域,提高图像的亮度;增加Sobel算子的梯度计算模板,使受检测的边缘更加完整;为了保证图像尽可能的少出现断点情况,采用原始Bernsen算法与增加高斯滤波后的Bernsen算法得到的线性组合阈值,使得图像边缘更加连续。实验结果表明,本文算法能有效消除光照不均的影响,提高图像边缘检测的效率。
0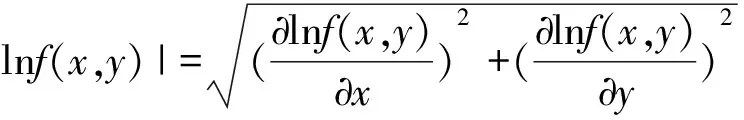

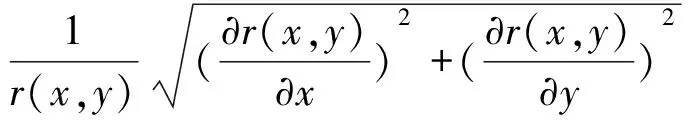
2.2 改进Sobel算子
[f(x-1,y-1)+2f(x,y-1)+f(x+1,y-1)],
[f(x-1,y+1)+2f(x-1,y)+f(x-1,y-1)],


2.3 边缘检测的阈值优化



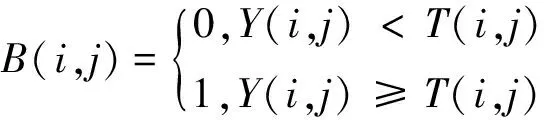
3 实验结果与分析
3.1 光照不均图像的预处理效果


3.2 对数域梯度预处理前后的检测效果比较


3.3 不同算法的边缘检测效果比较





4 结 论
