着水姿态对大型水陆两栖飞机着水性能的影响

2019-05-14廉滋鼎王明振褚林塘

船舶力学 2019年4期

孙丰，吴彬，廉滋鼎，王明振，褚林塘

（1.高速水动力航空科技重点实验室，湖北荆门448035；2.中航工业特种飞行器研究所，湖北荆门448035；3.中航通用飞机有限责任公司，广东珠海519000）

0 引言

水陆两栖飞机是可同时在水面和陆地起降的飞机，用途包括交通运输、水面搜救、森林灭火、旅游观光等，同时也可用于执行海上侦察、巡逻、反潜等任务。水上飞机在二战期间及战后一段时间内在军民用领域内扮演着重要的角色，但随着陆基飞机的优势逐渐体现，水上飞机的应用逐渐减少[1]。近年来随着通用航空在世界范围内的发展，水上/水陆两栖飞机作为通用飞机的一员再一次焕发了生机。目前国际上有代表性的水上/水陆两栖飞机机型有加拿大的CL-415、日本的US-2、俄罗斯的别-200 以及美国的LAKE 系列等，这些机型的性能体现了各个国家在相关研究领域的实力。国内进入21 世纪以来在水上/水陆两栖飞机研制上也开展了大量的研究工作，特别是大型水陆两栖飞机的成功立项，对着水性能要求较高，促进了着水冲击研究的开展。

着水性能是体现水陆两栖飞机水面起降性能的重要方面，表征着水性能的要素主要包括着水载荷、运动响应、喷溅程度等。欧美发达国家从上世纪40 年代开始对水上飞机着水冲击问题做了大量的研究工作，形成了完善的理论体系，并通过大量的缩比模型和少量的全尺寸模型试验对理论方法进行了验证，建立了试验数据库，形成了适用于工程应用的经验公式或半经验公式。美国国家航空航天局（NASA）的前身在早期的研究中做出了重要贡献[2-10]，Mayo 针对经典Wagner 理论的局限性进行了分析与讨论，认为Wagner 方程中由于忽略了下洗流的动量，导致其只适用于无纵倾垂直入水问题，通过在动量方程中引入下洗流动量项获得了通用性更强的动量方程，允许带有纵倾角和水平速度的真实水上飞机冲击问题的分析得以实现。其后，Milwitzky，Steiner，Robert，Miller 等在Mayo 理论的基础上分别做了改进，完善了水上飞机入水冲击理论，使得过载、压力、转动力矩和运动响应的理论分析得以实现。

国内相关研究成果较少，但有关船舶及水中兵器的入水冲击研究涌现了一大批成果，这些成果可借鉴到水上飞机的着水分析中。龚丞等[11]结合势流理论计算和CFD 技术各自的优势，给出了一种快速地再现甲板砰击现象的数值模拟方法，结果表明能够比较准确地模拟甲板上浪过程，冲击载荷与试验吻合良好，表明该方法能够分析预报甲板上浪冲击载荷。王文华等[12]采用一种新的CFD 方法模拟了二维弹性楔形结构的自由入水过程，建立不同状态参数的弹性楔形结构自由入水模型，研究了各参数对自由入水弹性楔形结构的整体运动性能和局部变形响应的影响。陈立霞[13]基于Von Karman 和Wagner的水动力冲击理论，将机身简化为V 形楔形体，建立简化的刚体运动方程，对其求解得到楔形底部直升机着水载荷和压力分布估算方法。

水上/水陆两栖飞机在水面降落的最佳着水姿态角选取中要求着水载荷和响应应尽可能小，因此开展不同初始姿态角的着水性能分析是必要的。为了解决气动力差异对模型试验和仿真结果的影响，本文提出了采用单船身模型进行着水试验和仿真，目的是分析不同初始纵倾角下的着水载荷和运动响应，验证着水性能设计，确定最佳的着水姿态。

1 仿真与试验模型说明

试验与仿真模拟水陆两栖飞机单船身模型平静水面着水，主要控制参数包括着水姿态、速度等。着水模型属于动力相似模型，缩比模型与实机需满足傅汝德数相似准则[14]，表1 给出了各参数由实机转化到模型的缩比关系。仿真模型与试验模型采用相同的缩尺比，这样做的目的是提高计算精度，虽然当实尺度模型与缩比模型的网格数相同时，由于实尺度模型网格尺寸大，使得显示分析的时间步长大，计算效率会有所提高，但此时实尺寸模型的网格尺寸无法满足计算结果的收敛性。缩尺比效应会对仿真结果造成一定的影响，但是通过缩比模型与实尺寸迫降数据对比发现缩比模型能够保证足够的精度[15]。

表1 全尺寸飞机与模型转化关系Tab.1 Scale relationships between real aircraft and model

试验模型是基于傅汝德数相似准则制作的，不能保证气动力的相似性，同时在LS-DYNA 软件中同时模拟气动力和水动力也是困难的，因此基于以上问题的考虑，去掉计算模型和试验模型上的机翼及尾翼，只保留机身部分，即单船身。这样处理首先可排除仿真和试验中气动力不一致对着水性能分析的影响，而气动力对于船体本身着水性能的定性分析结果影响很小；其次降低了模型试验制作和仿真建模的工作量，提高建模效率；最后翼展的消失使得流场规模大大缩小，计算效率得以大幅提高。

使用非线性有限元软件LS-DYNA 对单船身着水过程进行仿真分析，飞机结构采用Lagrange 单元算法，流体采用ALE 单元算法，单元尺寸为0.02 m，满足计算结果收敛性要求[16]，采用罚函数方法求解耦合界面处的接触力。图1 为单船身着水的计算模型，包括单船身模型、水域和空气域。研究重点关注单船身的着水载荷和运动响应，结构的变形对二者影响较小，只有百分之几[17]，因此将单船身仿真模型做了刚性处理，这样既有利于提高计算效率，又可以通过刚体属性定义保证计算模型与试验模型的重量、重心位置以及惯量等参数的一致性。

图1 有限元模型Fig.1 FE model

2 试验设计

试验是在中国特种飞行器研究所的拖曳水池进行的，水池主尺度：池长510 m，池宽6.5 m，池深6.8 m，水深5.0 m。拖车性能：速度范围0.1～22 m/s，车速稳定精度优于0.2%。试验装置包括重心连接杆、滑车、升沉杆、电磁钩触发开关、电磁钩、电动缸和垂直运动控制机构等。该试验装置保证模型能在一定范围内上下前后自由运动，模型能绕重心位置点自由俯仰转动，如图2 所示。试验中拖车提供水平速度、电动缸提供垂直运动速度，着水姿态通过前后斜拉钢索进行调节，保证着水姿态。试验主要步骤是：拖车运行到指定水平速度时，给出电动缸预设的垂直速度指令；电动缸加速到指定垂直速度并触发电磁钩开关，模型与试验装置脱离；为保证试验数据的有效性，每次试验重复3 次，试验模型安装见图3。

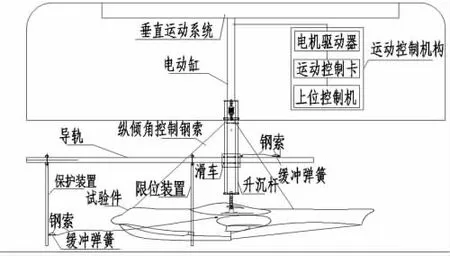
图2 试验件安装示意图Fig.2 The sketch map of model installation

图3 试验模型安装Fig.3 Model installation

试验时着水纵倾角（飞机水平基准线与静水面夹角）为4°、6°和8°，如图4 所示，由图4 基本可以判断出各个姿态角下飞机的着水位置。试验水平速度为10.02 m/s，下沉速度为1.67 m/s。为能够全面了解模型在着水时载荷大小及分布情况，以及着水过程中模型纵倾姿态角和重心处过载，需安装相应的传感器，布置方案如下：

（a）压力传感器

船体下表面沿龙骨方向预设了13 个压力传感器（型号：BCM520S-3，量程：0～300 kPa，精度0.1%），用来测量不同纵向位置处的压力，如图5 所示。

（b）垂直陀螺仪

在机身重心处放置一台垂直陀螺仪（型号：IMU610，角度量程：±90°，动态精度<0.3°，过载量程：±10 g，偏置稳定性：≦0.5 mg），测量模型纵倾角度和重心处过载。

图4 不同姿态角下机身与水平面相对位置Fig.4 The relative positions of the hull and water surface at different pitch angles

图5 压力传感器布置方案Fig.5 The layout of pressure sensors

3 结果分析

3.1 着水载荷分析

局部压力时间历程和船体表面的压力分布是水上飞机着水载荷研究关注的重点。选取初始姿态角4°工况下6 个典型位置处的压力随时间变化曲线分析，如图6 所示，压力曲线在冲击瞬间达到峰值，然后逐渐衰减，符合一般冲击载荷幅值高、脉宽窄的特性，除个别位置外，仿真与试验的压力峰值与变化趋势都吻合较好，该工况为断阶着水，最大压力发生在船艏方向距离断阶最近的4 号传感器位置，压力脉冲起始时刻代表遭遇冲击的先后。

图7 给出了船体底部龙骨处压力峰值沿船体纵向的无量纲分布，包括用于结构设计的理论计算值、7 个初始姿态角下的仿真计算值和3 个初始姿态角下的模型试验值，理论计算公式见参考文献[17]。图中纵轴Cp为各纵向位置处压力峰的无量纲值，由公式（1）计算得到，横轴Ld为测点距船艏的距离与模型长度的比，虚线标识处为船体断阶。由图可知，在所测量的区域内三种方法得出的结果总体分布基本吻合，受初始姿态角影响较小，根据理论压力分布设计的船体能够满足在所计算和试验的工况下的强度要求。理论计算值是用于指导结构设计的，不针对具体的着水工况，因此理论计算值应能涵盖各个工况下的载荷。

图6 典型位置处压力时历曲线Fig.6 The pressure-time curve of typical locations

压力分布的理论计算值同仿真计算和试验测量结果的主要差别及成因讨论：

（1）除在断阶处外，前体和后体的理论计算压力都是连续分布的，但试验和仿真结果显示在靠近断阶后的一段距离内没有压力的出现；断阶的存在使得断阶后距离断阶较近的区域在着水过程中不会与水接触，这个区域的尺寸有待于进一步研究。

（2）峰值压力的理论计算值在艉部较小的范围内出现了较大的增长，且较仿真和试验值大得多；理论结果受计算部位的船体斜升角影响较大，在靠近艉部的区域斜升角出现了较大的变化，导致压力大幅增加。这种现象只有在着水姿态较大的艉部着水时才会出现，但艉部着水时会存在明显的伯努利效应，会使得冲击压力得到有效降低。因此这种较大的艉部压力是不合理的，需在结构设计中引起注意。

（3）后体压力的纵向分布上，理论计算曲线基本为平滑过渡，而仿真和试验结果在后体中部出现了明显的波动峰，尤其是初始姿态角6°工况，后体中部的9 号测点处压力峰值的仿真计算值和试验值都超过了理论值；这种差异可能是理论公式自身的缺陷造成的，理论公式将各位置处的剖面处理成为独立的二维平面，没有考虑到各剖面的差异引起的相互影响。

图7 压力峰值纵向分布Fig.7 The longitudinal distribution of peak pressure

式中：p 为测点处压力；ρ 为水的密度；V 为着水速度。

3.2 运动响应分析

图8-9 为飞机在着水过程中的垂向冲击加速度时历曲线和姿态时历曲线，图中分别包含了各个初始姿态角的仿真计算结果和相应工况的试验值。在所计算的工况中，3°-6°为断阶着水，7°-9°为船艉着水，由图8 可以看出艉部着水与断阶着水的加速度曲线在达到峰值前略有差异，如图中7°-9°曲线的平缓段，同时加速度峰值出现时间延后。这种现象是由艉部着水时偏心冲击带来的低头力矩引起的，随着艉部着水时姿态角的增大，偏心冲击带来的影响越大。

偏心冲击的影响在图9 中同样得到了体现，图中艉部着水的三个工况姿态角在着水后呈现先减小后增大的变化，而断阶着水工况姿态角先增大到峰值后逐渐减小。图8-9 中仿真与试验的曲线吻合度都较高，仿真及试验方法的有效性得到了互相验证。由两图的时间轴可以看出姿态的变化滞后于加速度，这种滞后可从两个方面判断：一是偏心冲击影响的作用时间，所有工况的加速度曲线受偏心冲击影响体现在0.05 s 前，而在姿态曲线中体现在0.3 s 之前；二是加速度峰值和姿态峰值的出现时间，加速度峰值都出现在0.1 s 之前，过载峰值出现在0.4 s 之后。

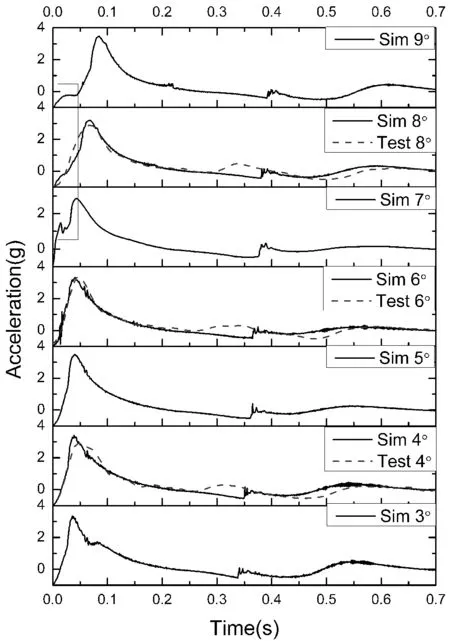
图8 各工况下的加速度Fig.8 The acceleration at different cases

图9 各工况下的姿态角Fig.9 The pitch angle at different cases

图10 各工况下加速度和姿态峰值Fig.10 The acceleration and pitch angle peak at different cases

对不同初始姿态τ 下的加速度峰值和姿态峰值进行统计，如图10 所示，加速度峰值在断阶着水工况（3°-6°）相差不大，但在6°-9°间出现了明显的波谷，姿态峰值的变化随着初始姿态角的增大呈现先减小后增大的变化。因此可以认为，从降低冲击载荷和姿态变化幅值的角度考虑，较好的着水姿态为6°-8°，7°最佳。