基于机器学习的页岩气产能非确定性预测方法研究
2019-05-13马文礼李治平孙玉平张静平邓思哲
马文礼,李治平,孙玉平,张静平,邓思哲
(1.中国地质大学(北京),北京 100083;2.非常规天然气能源地质评价与开发工程北京市重点实验室,北京 100083;3.中国石油勘探开发研究院,河北 廊坊 065007;4. 中国华腾工业有限公司,北京 100080)
0 引 言
页岩气的高效开发对优化中国能源结构、保障中国能源安全意义重大[1-3]。页岩气井钻前产能预测是页岩气开发方案制订与优化的重要环节,可为页岩气开发投资风险的评估提供依据。由于页岩气开发受很多不确定性因素影响,使得目前在页岩气的实际生产中,确定性的产能预测方法可靠性差[4-10]。考虑页岩气开发的不确定性,开展页岩气产能非确定性预测方法研究,是解决上述问题的有效途径。然而,现有的页岩气产能非确定性预测方法仅适用于投产后的页岩气井[11-15],缺少适用于页岩气井钻前产能非确定性预测的方法。针对上述问题,建立了一种适用于页岩气井钻前产能非确定性预测的方法,新方法可利用已投产井的地质、工程及生产数据,预测了拟钻页岩气井投产后的产能概率区间,包括页岩气井的产能上限与下限,以及每种可能产能动态的概率。运用该方法,可在页岩气井钻前快速获得较为可靠的、基于概率的产能信息。
1 基于机器学习的页岩气产能非确定性预测方法原理
页岩气产能非确定性预测方法的实施流程如图1所示。
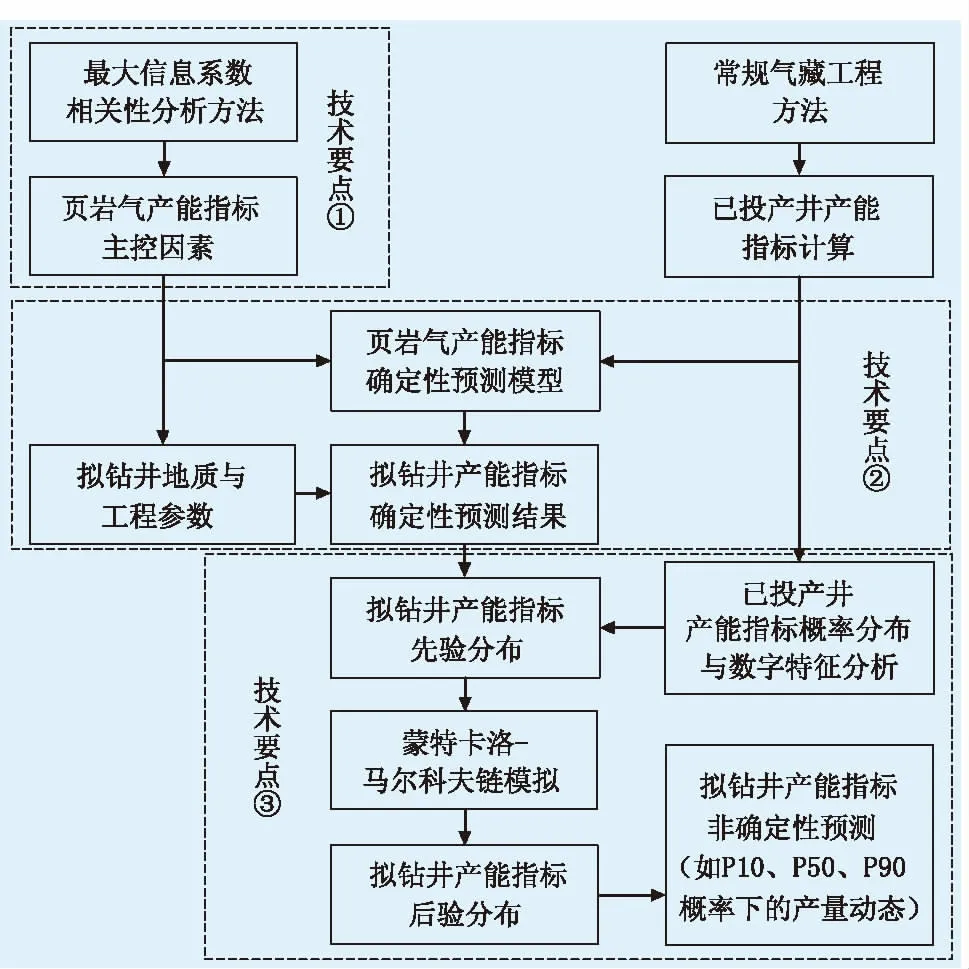
图1 基于机器学习的页岩气产能非确定性预测方法流程
1.1 页岩气产能指标主控因素分析
技术要点①选用参考文献[16]提出的最大信息系数相关性分析方法,定量分析影响页岩气产能指标的各种地质因素与工程因素,所确定的主控因素将作为下一步建立产能指标确定性预测模型的输入变量。利用最大信息系数分析变量之间相关性的核心思想是:制作2个变量的散点图,将该散点图网格化后,变量之间相关性越强,散点图中的点应包含在越少的网格之内。基于这一原理,不仅可以识别变量之间的线性相关关系,也可以探测非线性相关关系,这是传统Pearson相关系数不具备的优点。
1.2 页岩气产能指标确定性预测模型建立
支持向量机(SVM)立足于严密的数学分析,当处理小样本时,模型泛化能力更强,不易出现过拟合的问题[17-20],文中选用支持向量机技术建立页岩气产能指标确定性预测模型。通常支持向量机需要借助优化算法选择最优的初始参数,而遗传算法(GA)和粒子群算法(PSO)往往是首选。然而,传统的遗传算法局部搜索能力较弱且收敛速度慢,传统的粒子群算法由于缺少变异性容易陷入局部最小化[21-23]。考虑到经典遗传算法与粒子群算法的各自优势,提出一种混合优化算法(HGAPSO),用以优化支持向量机的参数。该算法的核心思想是将经典遗传算法的演化算子集成到经典粒子群算法中,以弥补其劣势。图2为HGAPSO的计算流程,由图2可知,每一次迭代过程,在更新了所有粒子的速度和位置后,将演化算子(选择、交叉、变异)随机应用到一部分粒子之中,产生了一些新粒子,新粒子增加到粒子群中,解决了经典粒子群算法容易陷入局部最小的问题。

图2 利用HGAPSO优化SVM模型的流程图
1.3 页岩气产能非确定性预测
通过技术要点②预测拟钻页岩气井的产能指标,计算得到该拟钻井确定性的产量动态q。通过对已投产页岩气井产能指标的统计分析,估计拟钻页岩气井产能指标的先验分布。基于文献[12],开展“蒙特卡洛-马尔科夫链”模拟,预测拟钻页岩气井产能指标后验分布,在此基础上对该井产量动态进行非确定性预测。拟钻页岩气井产能指标后验分布的“蒙特卡洛-马尔科夫链”模拟步骤如下。
(1) 在各产能指标先验分布中抽取一组样本Xproposal,运用常规气藏工程方法,计算得到该产能指标样本下的产量动态qproposal。
(2) 按下式计算判定系数α。
(1)
式中:α为判定系数;σt-1为上一时间步由随机抽取的产能指标Xt-1计算得到的动态产量qt-1与预测确定性的动态产量q之间的标准差;std为计算标准差函数;σproposal为当前时间步由随机抽取的产能指标Xproposal计算得到的动态产量qproposal与预测确定性的动态产量q之间的标准差;σ为所有已投产井计算产能指标时拟合误差的均值;q为利用技术要点②预测的产能指标计算得到的日动态产量,m3·d-1;qproposal为利用当前时间步随机抽取的产能指标Xproposal计算得到的日产量动态,m3·d-1;qt-1为利用上一时间步随机抽取的产能指标Xt-1计算得到的日产量动态,m3·d-1。
(3) 从均匀分布U(0,1)抽取随机数u。
(4) 如果α>u,则Xt=Xproposal,t=t+1,并返回步骤(1);否则,放弃Xproposal,返回步骤(1),重新抽取一组样本Xproposal。
(5) 当获得足够数量的产能指标样本后,结束迭代,并进行统计分析,获得产能指标后验分布。
2 实例应用
为了验证文中方法的可行性,选取中国24口页岩气井进行算例分析。首先收集各井的地质参数、工程参数及产量数据,选用Arps双曲递减模型计算各井产能指标,拟合得到各井的初期最大产气量、初期递减率及递减指数,得到由24口井组成的计算数据集。表1为数据集中各参数的主要统计指标。
随机选取1口井(W井)作为拟钻页岩气井,剩下的23口井作为已投产页岩气井,开展页岩气产能非确定性预测算例分析,即随机用23口井数据对另外1口井产能进行非确定性预测。运用最大信息系数相关性分析方法,确定有机碳含量、含气量、总液量、单段液量、总砂量、单段砂量、用液强度、加砂强度等8个参数为主控因素。以这8个因素为输入变量,以初期最大产气量、初期递减率及递减指数为输出变量,运用混合支持向量机技术HGAPSO-SVM,训练产能指标确定性预测模型,运用训练好的模型确定性预测拟钻井的产能指标。
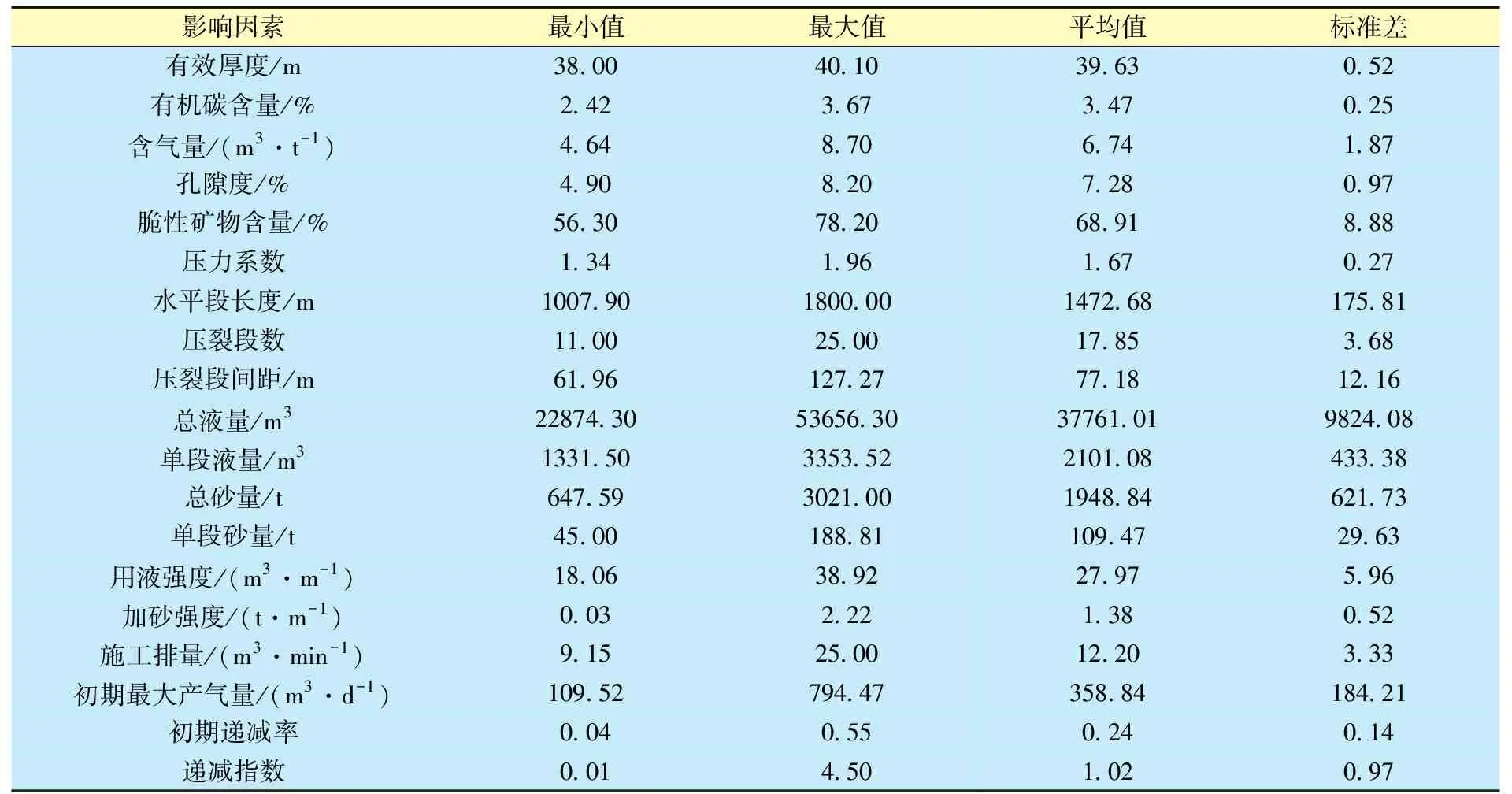
表1 数据集中各参数的主要统计指标
本算例仅考虑初期递减率与递减指数的不确定性。通过前人研究成果,初期递减率满足对数正态分布,递减指数满足正态分布。统计分析23口已钻页岩气井的产能指标可知,初期递减率的样本均值与方差为0.24与0.02,递减指数的样本均值与方差为1.02与0.41。由此可以确定拟钻井的初期递减率与递减指数的先验分布。根据已投产井计算产能指标时的拟合误差,确定σ2为0.03。利用“蒙特卡洛-马尔科夫链”模拟方法预测拟钻井的初期递减率与递减指数的后验分布,在此基础上进行该拟钻井产能的非确定性预测。
不同于确定性产能预测方法,文中方法对拟钻页岩气井产能预测的结果不是一个确定的产能动态,而是一个范围,这个范围包含了这口井的产能上限与产能下限,以及上、下限之间每个可能的产能动态发生的概率。
图3为利用文中方法对W井产能进行非确定性预测的结果。图中P90、P50与P10曲线分别代表在90%、50%、10%概率下W井所能达到的产能水平,P90曲线代表W井的产能下限,P10曲线代表W井的产能上限,W井投产后的产能曲线很可能会落在P90曲线与P50曲线之间的区域(概率超过50%)。对比W井实际产量,可见利用该方法对W井产能的非确定性预测结果是可靠的。
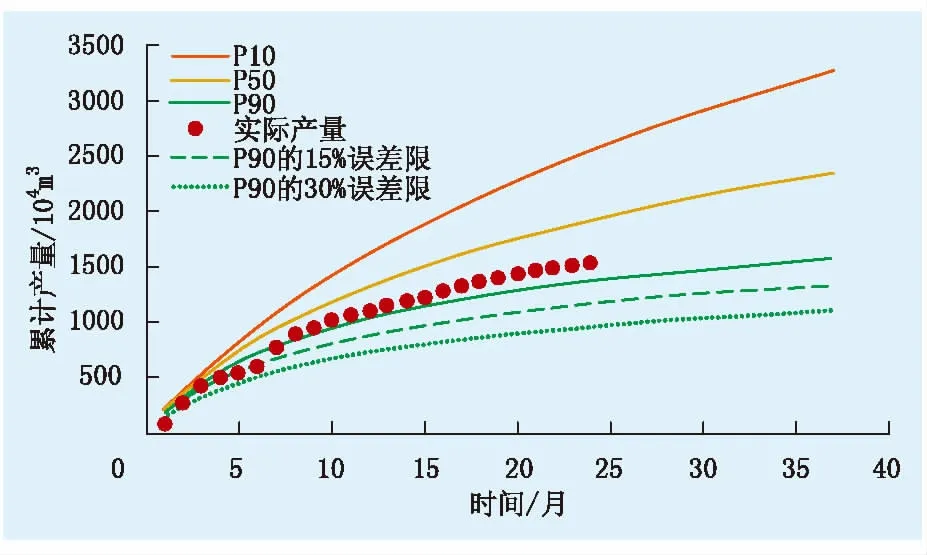
图3 W井产气量的非确定性预测结果
产能非确定预测模型可靠性的评价方法与传统方法存在差异。文中结合页岩气现场生产实践,制订了适用于页岩气产能非确定性预测模型的可靠性评价方法。该评价方法实施步骤如下:①对若干口拟钻页岩气井产能进行非确定性预测,将各井产能非确定性预测结果与该井实际产量进行对比;②如图3所示,将P90的30%误差限与P10之间的区域称为“准确率评价区间”,将P90的15%误差限与P50之间的区域称为“大概率事件区间”;③若1口井有超过70%的实际产量数据落在“准确率评价区间”,则认为这口井的非确定性预测结果是“可靠”的,将这类井的占比称为模型的“准确率”,若“准确率”超过70%,则认为该模型具有较高的预测精度;④若1口井有超过50%的实际产量数据落在“大概率事件区间”,则认为这口井的非确定性预测结果属于“大概率事件”,若这类井的占比超过50%,即大概率事件发生的概率超过50%,则认为该模型预测结果满足概率统计规律;⑤若模型具有较高的预测精度,同时预测结果满足概率统计规律,则认为该模型是可靠的。
根据上述可靠性评价方法,将24口井逐一作为拟钻井进行预测。预测结果表明:利用文中方法进行产能非确定性预测的准确率为70.8%,预测结果为“大概率事件”的井占54.2%,说明该方法具有较高的预测精度,且预测结果满足概率统计规律。将该方法用于页岩气井产能非确定性预测是可靠的。
3 结 论
(1) 文中提出了一种基于机器学习的页岩气产能非确定性预测方法,该方法将最大信息系数相关性分析方法、混合支持向量机技术HGAPSO-SVM及“蒙特卡洛-马尔科夫链”模拟有机结合,可利用已投产井的地质及工程数据对1口拟钻页岩气井未来的产能进行非确定性预测。
(2) 选取中国24口页岩气井算例,分析结果表明:利用文中方法进行产能非确定性预测的准确率为70.8%,预测结果为“大概率事件”的井占54.2%,说明该方法具有较高的预测精度且预测结果满足概率统计规律。
