基于数据挖掘的长短期记忆网络模型油井产量预测方法
2019-05-13谷建伟李志涛贾祥军
谷建伟,周 梅,李志涛,贾祥军,梁 颖
(1.中国石油大学(华东),山东 青岛 266580;2.中国石化胜利油田分公司,山东 东营 257000)
0 引 言
产量预测是油藏动态分析的重要内容,前人在该方面已进行大量研究,提出各种产量预测方法,可分为基于统计分析的经典油藏工程方法[1]和BP神经网络预测模型[2]两大类。基于统计分析的经典油藏工程方法在矿场中广泛应用,例如Arps产量递减模型。该类方法经过统计大量油井、油藏产量表观参数后形成,简单明了,但是适用条件苛刻,应用范围小,具有一定局限性[3]。BP神经网络模型广泛应用于产量预测[4-5],先后发展了蚁群算法、遗传算法[6],这些优化算法通过对历史生产数据深度学习,抓取数据之间隐藏的规律,通过对模型进行训练优化,建立多变量的产量预测模型,捕捉多种生产数据与产量之间的隐藏规律,与传统的油藏工程方法相比预测结果更加可靠[7]。
油井产量预测是基于油井生产历史的典型时间序列预测问题[8],目前传统BP神经网络及其改进后的预测模型在处理时间序列数据时,没有考虑历史时间序列数据影响,相当于每个样本独立训练,没有时序观念[9]。针对油井产量变化的普遍特征,提出采用长短期记忆神经网络(LSTM)预测模型来进行产量预测。该模型是一种时间递归神经网络模型,具备时序观念,具有长时间的记忆能力,属于典型的深度学习模型,能够更深层次挖掘数据之间的潜在规律,使预测变得更加准确可靠[10-12]。
1 基于长短期记忆神经网络的模型建立
1.1 循环神经网络(RNN)原理
长短期记忆网络(LSTM)是基于循环神经网络(RNN)改进的一种算法[13-14]。RNN将上一时刻的隐藏层状态信息应用于当前输出的计算中(图1),当输入为时间序列时,可以将其展开为一系列相互连接的标准神经元。图1中,xt为t时刻的输入信息;ht为t时刻隐藏层的状态;yt为最终输出信息;W、U、V为各层之间权重系数矩阵。展开的循环神经网络结构图中,相同位置参数W、U、V是共享的,大幅度减少了需要学习的参数。
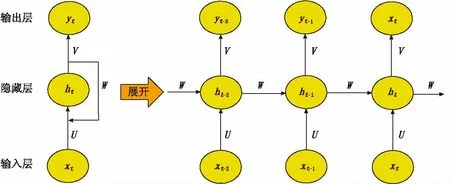
图1 循环神经网络单元构成
RNN的原理如下:给定时间序列x=[x1,x2,…,xt-1,xt],循环神经网络将展开成一个隐含层数量为t个的循环神经网络RNN。循环神经网络的传播过程可以用如下公式表示:
ht=f(Uxt+Wht-1+b)
(1)
yt=f(Vht+b)
(2)
式中:ht-1为t-1时刻隐藏层的状态;b为偏置项;激活函数f一般为tanh函数或者Relu函数。
RNN不同于传统神经网络的地方在于隐藏层的输入有2个来源,一个是当前的输入xt信息,另一个是上一个状态隐藏层的输出ht-1信息,而传统神经网络的输入只能是上一层的输入(输入层的输入或者隐藏层的输出)。
在应用RNN模型过程中发现,当时间间隔不断增大时,RNN会丧失学习过去较久远信息的能力,即在反向传播过程中出现梯度消失现象,导致模型预测误差大[15]。
1.2 长短期记忆网络原理
为了解决RNN梯度消失的问题,在RNN神经网络的隐藏层引入LSTM细胞结构单元取代原来的隐藏层单元,形成LSTM神经网络模型[16-18]。LSTM细胞结构单元的运算流程如图2所示。
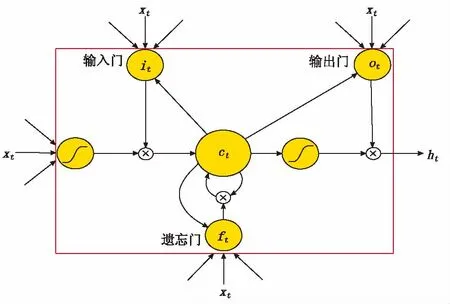
图2 LSTM细胞结构单元构成
LSTM结构单元主要包括输入门、输出门、遗忘门和自连接的记忆单元状态值。LSTM模型中输入门、输出门和遗忘门的主要作用是为了控制信息的传递,控制有多少信息能够传递给当前神经元,分配多少当前神经元的信息至下一个神经元,其取值均与xt、ht-1和ct-1取值有关[9]。
输入门、输出门和遗忘门可以表示为:
it=σ(Wxixt+Whiht-1+Wcict-1+d)
(3)
ot=σ(Wxoxt+Whoht-1+Wcoct-1+d)
(4)
ft=σ(Wxfxt+Whfht-1+Wcfct-1+d)
(5)
式中:it为t时刻输入门的输出;ot为t时刻输出门的输出;ft为t时刻遗忘门的输出;ht-1为t-1时刻隐藏层的输出;ct-1为t-1时刻记忆单元状态值;σ为激活函数;d为对应的偏置项;Wxi为输入层与输入门之间的权值系数矩阵;Whi为隐藏层与输入门之间的权值系数矩阵;Wci为记忆单元与输入门之间的权值系数矩阵;Wxo为输入层与输出门之间的权值系数矩阵;Who为隐藏层与输出门之间的权值系数矩阵;Wco为记忆单元与输出门之间的权值系数矩阵;Wxf为输入层与遗忘门之间的权值系数矩阵;Whf为隐藏层与遗忘门之间的权值系数矩阵;Wcf为记忆单元与遗忘门之间的权值系数矩阵。
t时刻记忆单元状态值由2部分组成,分别为上一时刻的记忆单元状态值和当前的候选记忆状态值Wxcxt+Whcht-1+d,这2个部分分别由输入门和遗忘门控制,具体算法为:
ct=ftct-1+ittanh(Wxcxt+Whcht-1+d)
(6)
式中:ct为t时刻记忆单元状态值;Wxc为输入层与记忆单元之间的权值系数矩阵,Whc为隐藏层与记忆单元之间的权值系数矩阵。
LSTM结构单元中的记忆单元细胞可以在较长的一段时间内储存信息,从而缓解梯度消失,实现长时间的记忆功能。最终输出值ht由输出门和当前记忆单元状态值共同作用得到。
ht=ottanh(ct)
(7)
1.3 基于长短期记忆网络的产量预测模型
LSTM模型的学习训练过程分为5个步骤:①从左到右传播时,按照模型计算方法计算模型的输出值;②将模型输出值与实际值比较,计算误差;③从右到左,按照网络层级和时间反向传播,将误差分配到每个LSTM细胞结构单元;④根据相应的误差项计算每个权重的梯度;⑤应用适应性动量估计优化算法更新权重[19]。神经网络学习训练结构如图3所示。
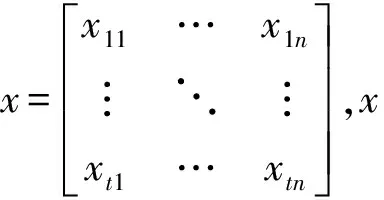
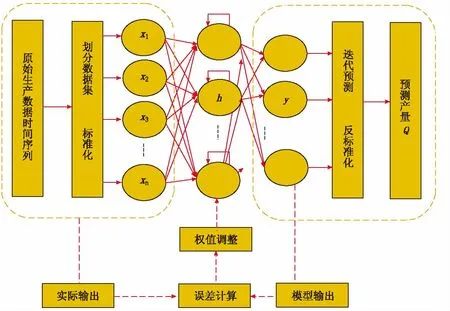
图3 基于LSTM的产量预测模型基本结构
模型中隐藏层为:
(8)
式中:xti为t时刻输入层中第i个节点值;uji为隐藏层第j个节点和输入层第i个节点之间的权值系数矩阵;htj为t时刻隐藏层第j个节点的输出值;ht-1,j为t-1时刻隐藏层第j个节点的输出值;wjj为反向传播时隐藏层第j个节点自连接的权值系数矩阵。
模型中输出层为:
(9)
式中:yt+k为输出层第k个节点的输出值;vkj为隐藏层第j个节点与输出层第k个节点之间的权值系数矩阵;b为偏置项。
模型向前预测产量的时间步长决定输出层节点数。该模型向前预测p个时间步长,则输出层节点数设定为p个,输出层输出时间序列y=[yt+1,…,yt+k,…,yt+p]。模型的输出值y在反标准化作用后得到最终的产量预测值Q,则产量预测值Q=[Qt+1,…,Qt+p]。
2 实例应用
2.1 样本选取
目标油藏DXY2位于东营凹陷中央隆起带中段,东营构造北翼,属于深湖—半深湖浊积扇沉积的砂岩透镜体油藏,油藏埋深为2 500~2 780 m,含油面积为2.2 km2,石油地质储量为529×104t。DXY2油藏从1969年投入开发,2000年后已投入开发22口油井、12口注水井。
根据月度生产数据的完整性、准确性、可获得性以及数据规模,选取其中7口油井作为研究样本对象。收集了这些井从投入开发至2017年11月的生产历史月度数据,分别将这些油井的生产历史月度数据划分为训练集和测试集,测试集为每口井最后一年的数据。训练集包含的期间月度生产数据作为模型的样本集,输入预测模型中进行学习训练,测试集中的生产数据将作为检验模型预测准确性的数据样本。该产量预测模型适用于任何井的产量预测,面对不同的输入样本,自动进行数据挖掘和深度学习,训练出专属于每口井的产量预测模型。
2.2 模型输入输出层节点数选择及数据处理
在产量预测模应用中需要确定模型输入层和输出层的节点数。根据油藏工程基本理论,油藏地质属性可以视为固定不变的因素,影响油井产量的可变因素较多,考虑样本参数特征,选取排量、泵深、生产天数、含水率、动液面、气油比、周围油井产液量、周围注水井注水量等8个指标作为输入层的输入变量。
在实际油藏中,每口油井邻近的注水井数量和油井数量具有不确定性,为方便计算,要求产量预测模型的输入样本矩阵固定列数,因此,首先需要对邻近注水井和油井进行数据清理,处理方法按照周围井与预测油井的距离进行综合考虑,距离越近,影响越大,距离越远,影响越小。具体处理方法如下:
(10)
(11)
式中:W为预测油井邻近注水井月注水量,m3/月;a为预测油井周围的注水井数,口;Wi为第i口注水井的月注水量,m3/月;di为第i口注水井与预测油井的距离,m;Q为预测油井邻近油井月产液量,t/月;b为预测油井周围的生产井数,口;Qj为第j口生产井月产液量,t/月;dj为第j口生产井与预测油井的距离,m。
经过处理后,可以得到每个待预测产量油井的样本集,将每个月度数据作为一组数据,可以得到从投产初期至2016年12月的所有样本,每个样本包括多个参数输入,x=[排量,泵深,生产时间,含水率,动液面,气油比,邻井注水量,邻井产液量],设定产量预测模型的输入层节点数为8个。
(12)
式中:xnorm为标准化处理后的值;xmax、xmin分别为生产数据集x中每个生产指标在不同时刻所有值中的最大值和最小值。
生产数据集经过标准化处理后,每个值均在[0,1],从而消除数据之间的量纲关系,使数据具有可比性。
模型的输出层节点数由向前预测的时间步长决定,考虑到预测1 a的月度产量变化,因此,将输出层的节点数设定为12个。
2.3 迭代次数及隐藏层节点数选择
产量预测追求的是预测结果的准确性和预测误差波动的稳定性,文中运用均方差(mse)评价模型分析预测值与实际值的拟合程度,均方差可采用式(13)计算,均方差越小,表明预测值与真实值之间的离散程度越低,预测结果更可靠[12]。
(13)
式中:y为实际产油量,t/月;y′为模型输出预测值,t/月;n为样本个数。
在确定模型的输入、输出层节点数后,还需要确定模型的隐藏层节点数,并选择合适的权值更新迭代次数。根据经验设定,令2个参数的初始值分别为100、1 000,然后调试不同的取值情况,以参数取值对应的模型均方差最小且趋于稳定为原则,最终确定目标油井的隐藏层节点数和权值更新迭代次数。
确定模型的输入层、隐藏层和输出层的节点数后,将预测井标准化处理后的样本集x输入模型,模型进行自动学习训练,输出产量预测值。
2.4 产量预测效果
利用形成的LSTM产量预测模型可以实现对油藏内任意生产井月产油量的预测,以DXY2X31井为例进行说明。将该井2016年11月之前的数据做为学习样本,进行深度学习和训练。以2016年12月至2017年11月的月度产油量作为检测数据,预测结果与实际检测数据对比,结果如表1所示。
由表1可知,模型预测值与实际值吻合性较好。从2016年12月至2017年11月,DXY2X31井预测月产油量与实际月产油量的平均误差为1.46%,满足工程计算的要求。因此, LSTM神经网络产量预测模型可以用于矿场应用。
比较模型预测值与实际数值之间的差异可知,在产油量出现突然大幅度增加、无预兆停产、大型作业措施、数据缺失等情况时二者会出现较大差异,其余时间内二者的数值差异小。另外,机器深度学习的一个显著特征是可以处理大量的数据,并在海量数据中挖掘出隐藏的价值,数据量越大,效果越好;反之,预测准确性降低。因此,该油藏2000年前数据部分缺失也是影响预测效果的一个原因。
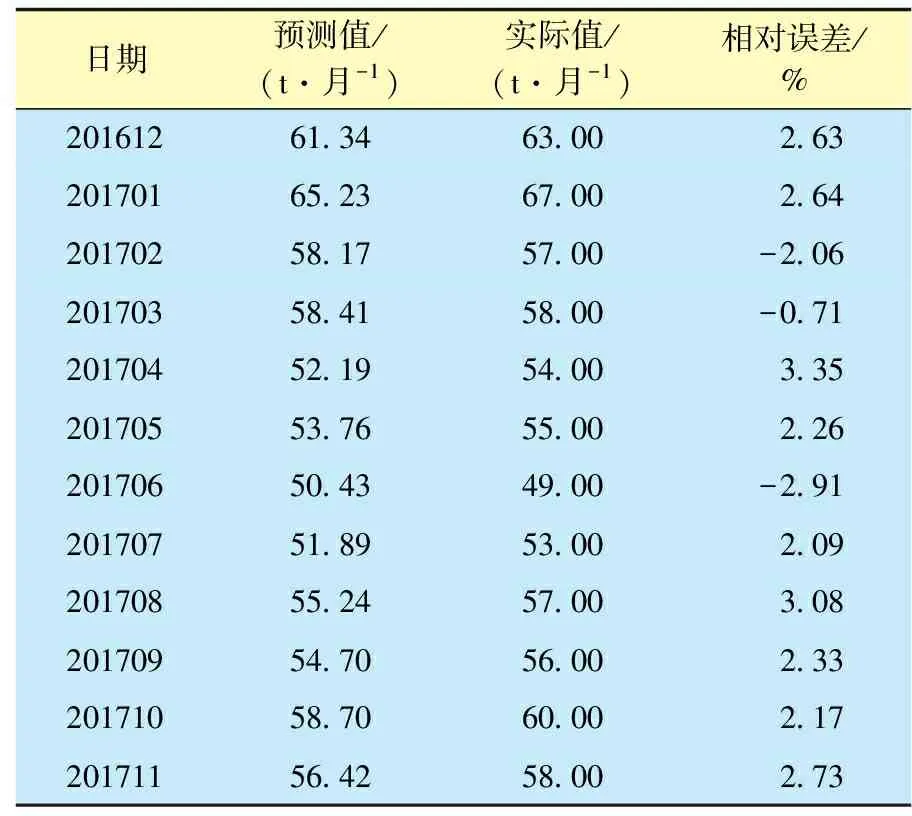
表1 DXY2X31井产量预测值与实际值对比
3 结论和建议
(1) 建立了基于长短期记忆网络模型的产量预测方法,确定了神经网络单元输入层、输出层、隐藏层参数的具体计算方法及样本建立、数据处理、学习过程的处理方法。建立的预测模型应用操作简单,面对不同的输入样本,模型自动训练学习,具有广泛适用性。
(2) 实例应用表明,形成的产量预测模型可以很好地预测油井产量变化,平均误差仅为1.46%,预测精度满足矿场要求。
(3) 基于目前的研究成果,可以进一步优化模型,如增加隐藏层的层数,检验多隐藏层LSTM网络结构的应用效果;进一步对油藏资料进行深入分析,筛选出表征大型措施、停产等特殊情况的参数类型。
