大跨度悬索桥施工阶段静风稳定性精细化分析

(浙江工业大学 建筑工程学院，浙江 杭州 310023)

悬索桥受力性能好，跨越能力强，是千米级主跨桥梁工程的首要选择。本世纪以来，桥梁工程建设由内陆跨越大江大河向跨海连岛等更宽广海域发展，悬索桥的跨径将进一步增大，潜在需求为2 000～5 000 m[1]。悬索桥结构跨度大、刚度小，风作用下的结构稳定性(包括静风和动力风作用的结构稳定性，前者主要指静风稳定性，后者则主要指颤振)已成为控制悬索桥设计和施工的重要因素。与动力风失稳相比，静风作用下结构失稳毫无预兆，突发性强，破坏性更大。此外，较之于成桥状态，施工状态的悬索桥结构边界约束更少，结构的整体刚度明显降低，导致结构抗风稳定性更差[1]。虽然施工阶段静风失稳检验风速可以降低，但是通常情况下悬索桥主梁架设期难以避开强风天气，因而悬索桥主梁架设期的抗风性能及控制研究颇受国内外学者的重视。随着悬索桥跨径的进一步增大和施工状态悬索桥刚度的显著降低，以下两个因素对施工期悬索桥静风稳定性的影响将可能更加突出：1) 静风作用下结构大变形导致的结构刚度和施加在结构上以结构变形为函数的静风荷载的非线性变化及其三维效应；2) 风速空间分布的非一致性。实测资料表明：风速沿着竖直高度和水平方向是变化的，但已有大跨度桥梁抗风分析中通常将桥址区域内的风速按均匀分布处理。悬索桥的主缆矢高和桥塔高度都比较大，桥面主梁一般采用竖曲线布置，依据风速的空间分布特性，桥面主梁、主缆和吊杆以及桥塔等构件上风速的差异性将更加明显，形成风速的空间非均匀分布。已有研究表明这些因素对悬索桥成桥状态的静风稳定性存在着重要影响[2-4]，但对施工状态大跨度悬索桥静风稳定性的影响如何，则需要进一步分析和明确。

至今，国内外学者对大跨度悬索桥的静风稳定性开展了大量的分析研究，研究主要集中在静风稳定性分析理论、成桥运营状态的静风稳定性以及静风失稳机理等方面[5-9]，对于施工状态悬索桥的静风稳定性研究则涉及不多。李翠娟等[10]采用三维非线性静风分析方法，对主跨3 500 m的CFRP主缆悬索桥进行了施工阶段的静风稳定性分析，探讨了3 种交叉吊索布置对施工阶段悬索桥静风性能的影响。吴士义[11]以云南澜沧江悬索桥为工程背景，运用增量和迭代相结合的静风效应分析方法，分析了悬索桥加劲梁架设期结构静风失稳的临界风速和结构静风效应。张新军等[12]对西堠门大桥开展了3 种不同主梁架设施工顺序的结构静风稳定性分析，揭示了主梁拼装过程结构空气静力稳定性的变化规律和适宜的主梁架设顺序。郭辉[13]和张新军[14]对三塔两跨悬索桥——泰州长江大桥开展了不同主梁架设施工顺序的结构静风稳定性分析，揭示了三塔悬索桥施工过程结构空气静力稳定性的变化规律以及适宜的主梁架设顺序。遗憾的是，上述悬索桥施工过程的静风稳定性分析中都没有考虑风速空间非均匀分布因素。为此，考虑结构和静风荷载的非线性以及风速空间非均匀分布等因素，建立了精细化的大跨度桥梁三维非线性静风稳定性分析方法，并编制了其计算程序。采用该程序，结合润扬长江大桥南汊悬索桥，模拟两种主梁架设顺序，分析大跨度悬索桥施工全过程静风稳定性的变化规律，探索适宜的主梁架设顺序，同时探明风速空间非均匀分布因素对施工状态悬索桥静风稳定性的影响，为确保大跨度悬索桥安全施工提供理论依据。

1 三维非线性精细化静风分析方法及程序

1.1 风速空间非均匀分布模型

桥址空间范围内平均风速可以表示为

U=μU0

(1)

式中：U0为参考点处的风速值，一般可以取中跨主梁跨中处的风速值；μ为风速空间分布系数，依据风场的实测资料[2]可以近似地表示为

μ=μH·μV

(2)

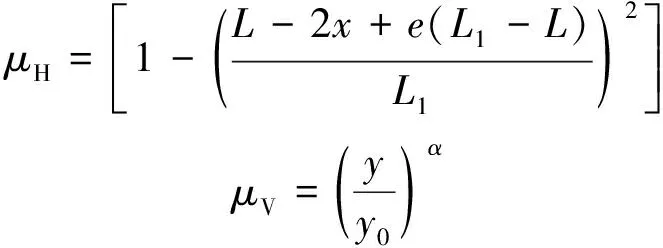
式中：μH为风速水平变化系数；μV为风速竖向变化系数；L为桥梁总长；L1为风场分布宽度；e为风场分布非对称性系数，0≤e≤1，e=0表示风速相对于主跨跨中水平对称分布；x为风速计算点至桥跨左端的距离；y为风速计算点处的离地高度；y0为参考点处的离地高度；α为地面粗糙度指数。

1.2 精细化风荷载计算模型

1.2.1 主梁静风荷载

风对桥梁结构的作用可以分解为平均风和脉动风作用。在平均风作用下，桥面主梁单位长度上受到的静风荷载可以分解为如图1所示的静力三分力即顺风向阻力Fz、横风向升力Fy和升力矩Mx。由于桥面主梁在静风作用下产生的变形会反过来改变来流风与桥面主梁间的相对攻角，使得作用在其上的静力风荷载的非线性变化及三维效应。考虑风速空间分布后，单位长度桥面主梁所受到的静风荷载可以表达为

(3)

式中：ρ为空气密度；D和B分别为主梁高度和宽度；Cz(αe)，Cy(αe)，CM(αe)为体轴下节段模型风洞试验测得的静力三分力系数；αe为有效风攻角，为来流风初始攻角θ0与静风作用下主梁的扭转角θ之和。

图1 作用在主梁上的静风荷载Fig.1 The aerostatic load acting on the girder

1.2.2 主缆和桥塔静风荷载

对于主缆、吊杆及桥塔等构件，静风荷载主要考虑顺风向的阻力分量，考虑风速空间分布后构件单位长度上所受的静风阻力为

(4)

式中：D为主缆和吊杆的直径或桥塔构件的迎风面宽度；CD为主缆和吊杆或桥塔构件的静风阻力系数，主缆和吊杆的阻力系数为0.7，桥塔的阻力系数为2.0。

1.3 静风平衡方程及其求解方法

在上述静风荷载作用下，结构将发生变形，达到一个新的平衡状态，即静风平衡状态，静风平衡状态的确定可以归结为求解结构几何和静风荷载双重非线性问题，即

[K(u)]{u}={F(u)}

(5)

式中：[K(u)]为结构的切线刚度矩阵；{F(u)}为结构所受的非线性静风荷载向量。

式(5)采用迭代法求解时，可以采用迭代求解方程，即

([KE]j-1+[Kσ]j-1){Δδ}j={Fj(αj)-
Fj-1(αj-1)} {δ}j={δ}j-1+{Δδ}j

(6)

式中：[KE]j-1和[Kσ]j-1分别为第j-1迭代步结束时结构的线弹性刚度矩阵和几何刚度矩阵；{Δδ}j为第j迭代步的位移增量向量；Fj(αj)为第j迭代步对应有效攻角为αj时结构所受的静风荷载向量；Fj-1(αj-1)为第j-1迭代步对应有效攻角为αj-1时结构受到的静风荷载向量。

式(6)的迭代求解可以采用静力三分力系数的欧几里得范数作为收敛准则，即

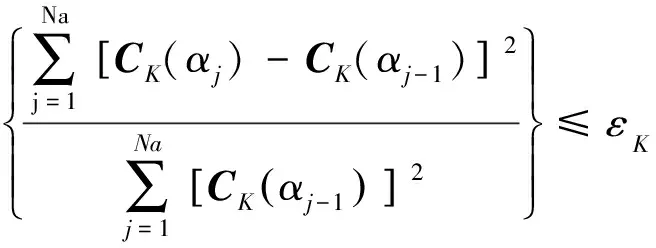
(7)

式中：Na为受到静风作用的主梁节点数；εK为设定的误差精度。

1.4 计算程序

基于上述分析方法，笔者提出了精细化的大跨度桥梁三维非线性静风稳定性分析方法，并编制了其计算程序(SNAA)，其求解思路和计算流程为

1) 采用基于CR列式法的结构三维几何非线性有限元分析方法，确定成桥状态结构的几何和内力状态，并根据式(1，2)计算各构件单元的风速空间分布系数。

2) 风速循环：Ui=Ui-1+ΔU

3) 在当前计算风速Ui下，按式(3，4)计算结构在初始风攻角下所受的静风荷载{F0}，并令{F2}={F0}，{F1}={0}。

4) 计算静风荷载增量{ΔF}={F2}-{F1}，并令{F1}={F2}。

5) 施加增量静风荷载，进行结构几何非线性有限元分析，获得新的结构平衡状态。

6) 计算主梁单元的有效风攻角，重新计算结构所受的静风荷载{F2}。

7) 计算静力三分力系数的欧几里得范数，检验其是否小于允许误差。若是，则迭代收敛，转到2)，增加风速，进行下一级风速的静风分析；若否，则回到4)，进行新一轮的迭代求解，直到满足收敛准则要求为止。

8) 若在某一级风速水平下，出现迭代不收敛，则回到上一级风速状态，减半风速增量ΔU，重新计算，直至风速增量小于预定的精度为止。

2 桥梁及主梁架设方案简介

润扬长江大桥南汊悬索桥是一座单跨悬索桥，中跨1 490 m，两侧边跨各470 m，见图2[15]。中跨主缆矢跨比为1/10，主缆横桥向中心距为34.3 m；吊杆纵桥向间距为16.1 m，共设91 对吊杆；桥面主梁采用全焊扁平流线型钢箱梁，总宽38.7 m，梁高3 m；桥塔为双柱三横梁混凝土门式框架结构，塔高约210 m。

图2 润扬长江大桥南汊悬索桥总体布置图Fig.2 General layout of Runyang bridge over the Yangtze River

如图3所示，悬索桥的主梁架设顺序按其推进方式通常有以下两种：一种是从中跨跨中处开始向两侧桥塔对称拼装，施工过程中始终只有一个架设梁段，梁段两端是自由的；另一种则是从两侧桥塔位置开始向跨中对称拼装，施工过程中有两个独立的架设梁段，梁段的一端自由，另一端支承在桥塔横梁上。笔者分别采用这两种主梁架设方法对润扬长江大桥施工过程的静风稳定性进行分析，主梁架设方案1和方案2施工阶段划分和梁段拼装情况分别如表1，2所示。

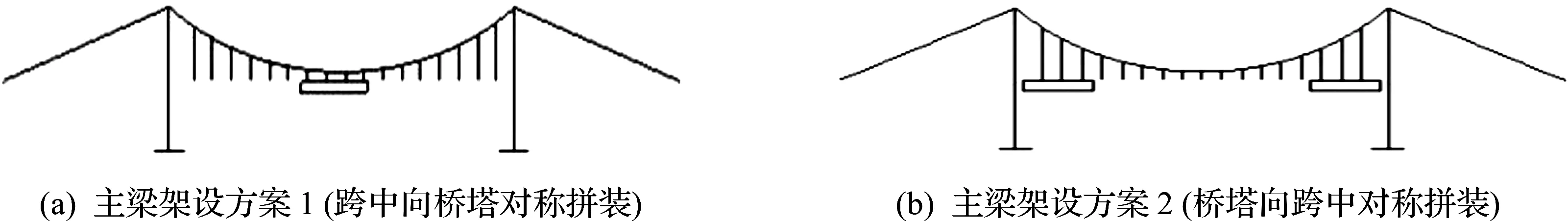
图3 主梁架设方案Fig.3 The deck erection sequences

表1 主梁架设方案1施工阶段划分和梁段拼装情况

Table 1 Construction stages and girder segments of deck erection sequence 1

施工阶段拼装率/%梁段数/节段拼装长度/m110.910161221.720322332.630483443.540644554.350805665.260966776.1701 127886.9801 288997.8901 44910100.0921 490

表2 主梁架设方案2施工阶段划分和梁段拼装情况

Table 2 Construction stages and girder segments of deck erection sequence 2

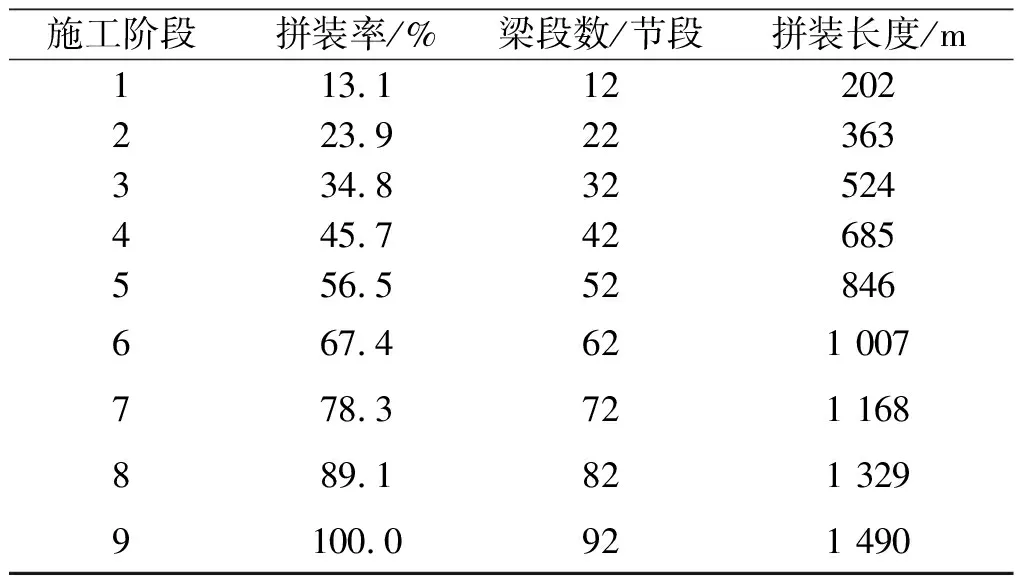
施工阶段拼装率/%梁段数/节段拼装长度/m113.112202223.922363334.832524445.742685556.552846667.4621 007778.3721 168889.1821 3299100.0921 490

3 悬索桥成桥状态静风稳定性精细化分析

在0°初始风攻角下，采用SNAA程序，对该桥成桥状态进行以下各种工况的静风稳定性分析：1) 风速空间一致分布；2) 仅考虑风速沿竖直方向的变化，水平方向均匀分布，即μH=1；3) 在风速沿竖直方向变化和风场关于主跨跨中左右对称(e=0)情况下，改变风场分布宽度L1为L，5L和10L，分析风场分布宽度对结构静风稳定性的影响；4) 在风速沿竖直方向变化和风场分布宽度L1=10L情况下，改变风场分布非对称性系数e为0，0.1，0.2，0.3，0.4，分析风场非对称分布对结构静风稳定性的影响。该桥桥位地表粗糙度横桥向按A类场地考虑，相应的地表粗糙度系数α取为0.12[15]。分析时，该桥离散为如图4所示的三维有限元分析模型，其中桥面主梁采用鱼骨式计算模型，主梁、塔柱及其横梁等采用空间梁单元模拟，主缆和吊杆则简化为空间杆单元，桥面主梁和吊杆间采用刚性横梁联系。分析所需的主梁静力三分力系数取该桥主梁节段模型风洞试验结果，如图5所示[15]。各计算工况下桥面主梁跨中处的位移随风速增加的变化趋势如图6，7所示。

图4 结构三维有限元分析模型Fig.4 Structural 3D finite element model

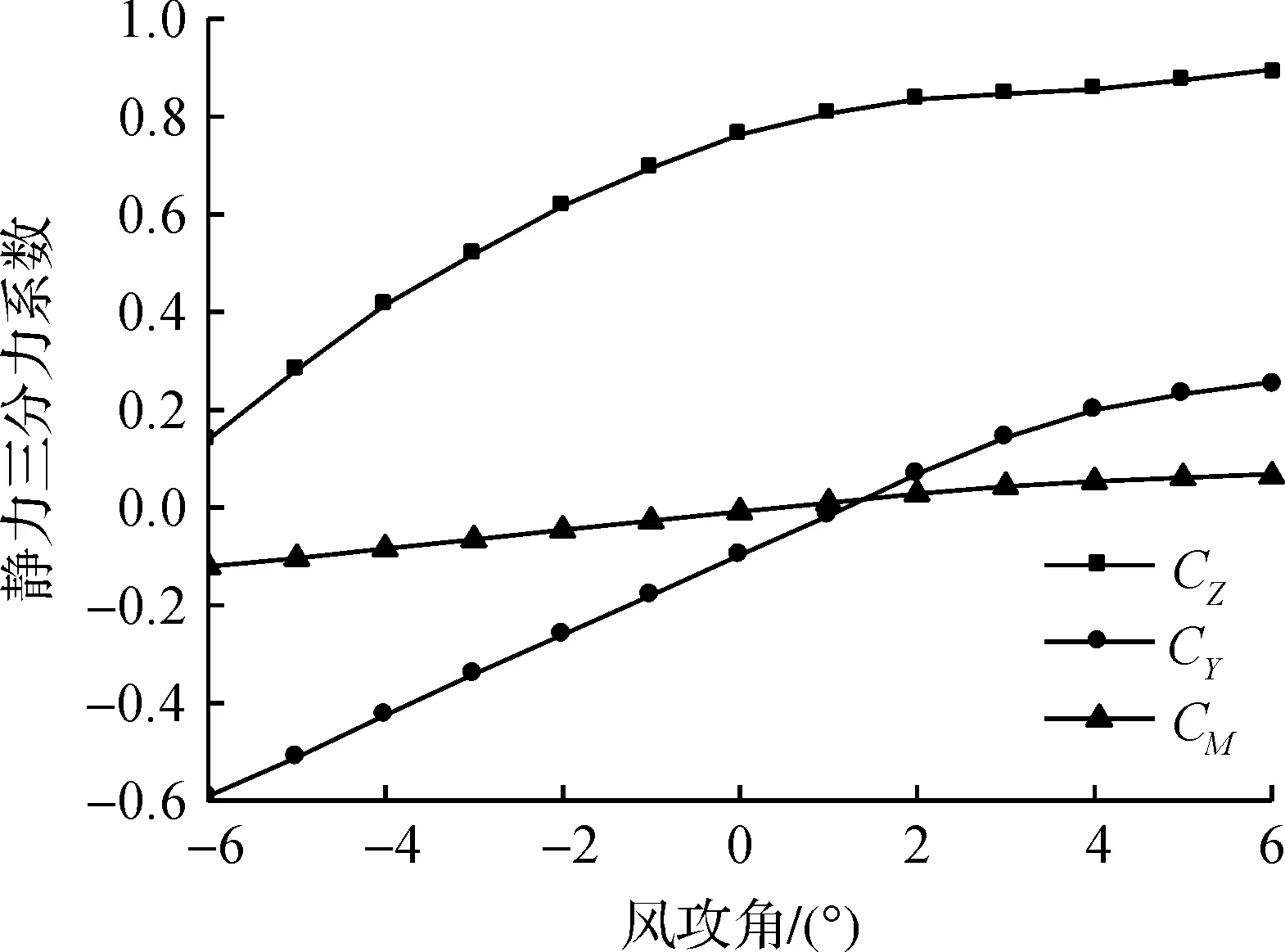
图5 主梁断面的静力三分力系数Fig.5 The aerostatic coefficients of girder

从图6可以看出：随着风速的逐渐增加，主梁跨中处的侧向位移呈现非线性的增长态势，而竖向和扭转位移很小，呈线性增长，但风速增加到100 m/s后，主梁跨中处的各向位移尤其是竖向和扭转位移都急剧增大，结构从稳定状态转向非稳定状态。需要指出的是，如图5所示，该桥主梁节段模型风洞试验测得的静力三分力系数为-6°～+6°，当风速达到100 m/s后主梁跨中处的扭转角急剧增大到+6°以上，故后续风速的静风分析缺乏实测的静力三分力系数，笔者分析时采用曲线外延插值近似得到，故不能预测得到结构真实的静风失稳临界状态。为了定性描述结构的静风稳定性，笔者定义了“静风失稳起始风速”，它是指随着风速的增加，结构位移突然剧增，结构开始由稳定转为不稳定状态所对应的风速值。因此，该桥成桥状态的静风失稳起始风速为100 m/s。

图6 风场分布宽度和竖向变化对主梁跨中处位移的影响Fig.6 Effect of wind distribution width and vertical variation on the girder displacements at midspan

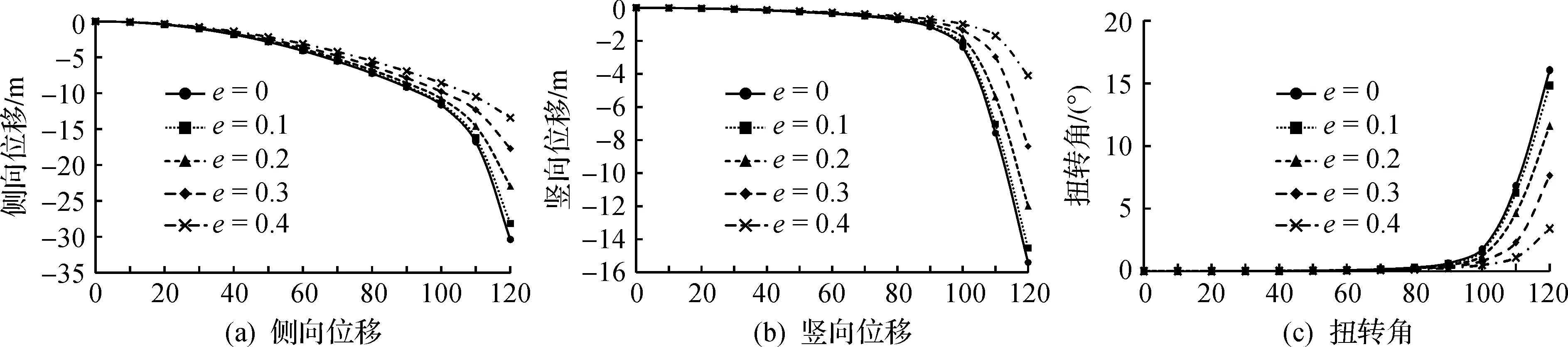
图7 风速非对称分布对主梁跨中处位移的影响Fig.7 Effect of wind speed asymmetrical distribution on the girder displacements at midspan

同时可以看出：考虑风速沿竖向变化后主梁跨中处的位移与风速空间均匀分布情况基本相同，风速沿竖向变化因素对该桥的静风稳定性不构成影响。在风场对称分布情况下，随着风场分布宽度的增加，结构位移逐渐增大，并向风速空间均匀分布情况逼近，当风场分布宽度L1达到桥跨长度的5倍以上时，结构位移与风速空间均匀分布情况基本一致。究其原因，如图8(a)所示，随着风场分布宽度的增加，桥面主梁各点的风速分布系数随之增大，趋向于均匀分布。因此，风场分布宽度对结构静风稳定性有一定的影响，当风场分布宽度L1达到桥跨长度的5倍以上时，可以不考虑此项因素的影响。

比较图7各种工况的结构位移发现：随着风场非对称参数e的增大，主梁位移显著减小，结构的静风失稳起始风速由100 m/s(e=0，0.1，0.2)增大到110 m/s(e=0.3，0.4)，结构的静风稳定性增强。如图8(b)所示，随着风场分布的非对称参数的增大，桥址区域内各点处的风速分布系数均明显减小，施加到结构上的静风荷载随之减小，结构的变形和内力因而减轻。

综上分析可知：风速沿竖向变化和风场分布宽度对悬索桥成桥状态的静风稳定性影响甚微，但风场非对称分布因素的影响则比较显著，在静风分析时应给予准确考虑，必要时需模拟地形在风洞中测试桥址处的风场分布系数以准确地预测结构静风失稳临界状态。

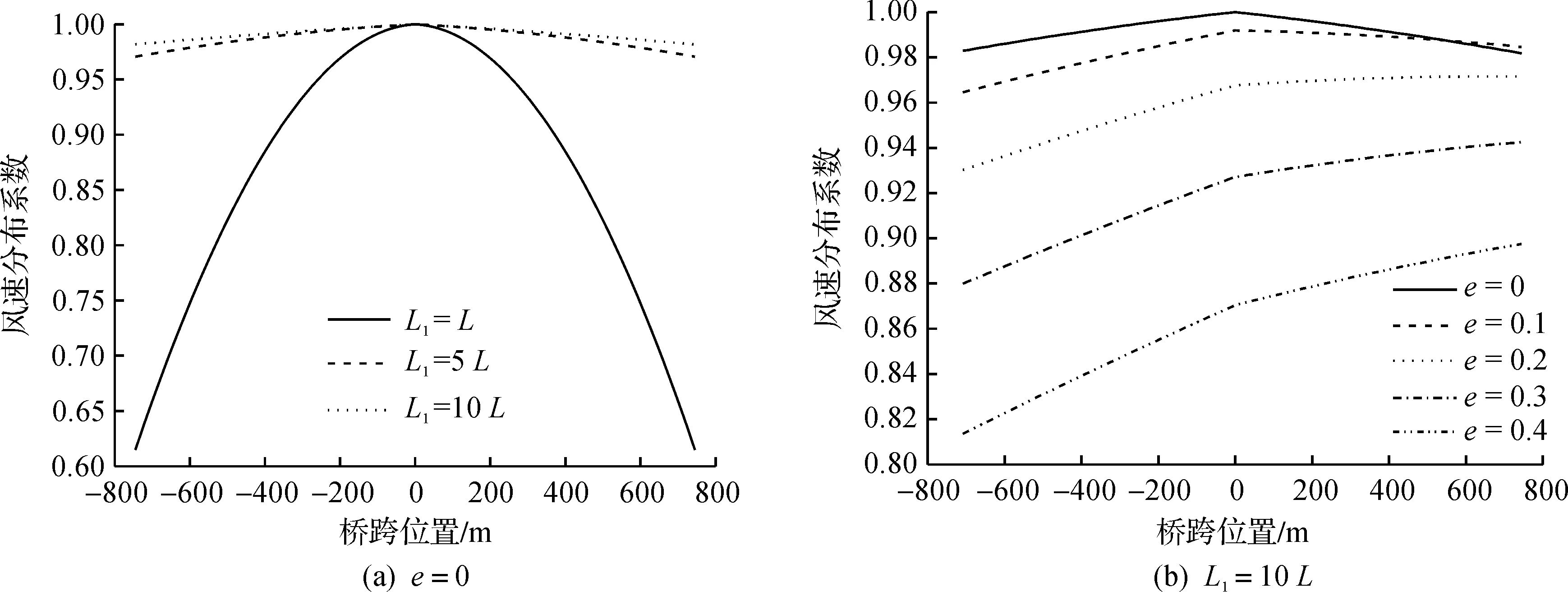
图8 风速分布系数Fig.8 Wind speed distribution coefficient

4 悬索桥施工阶段静风稳定性精细化分析

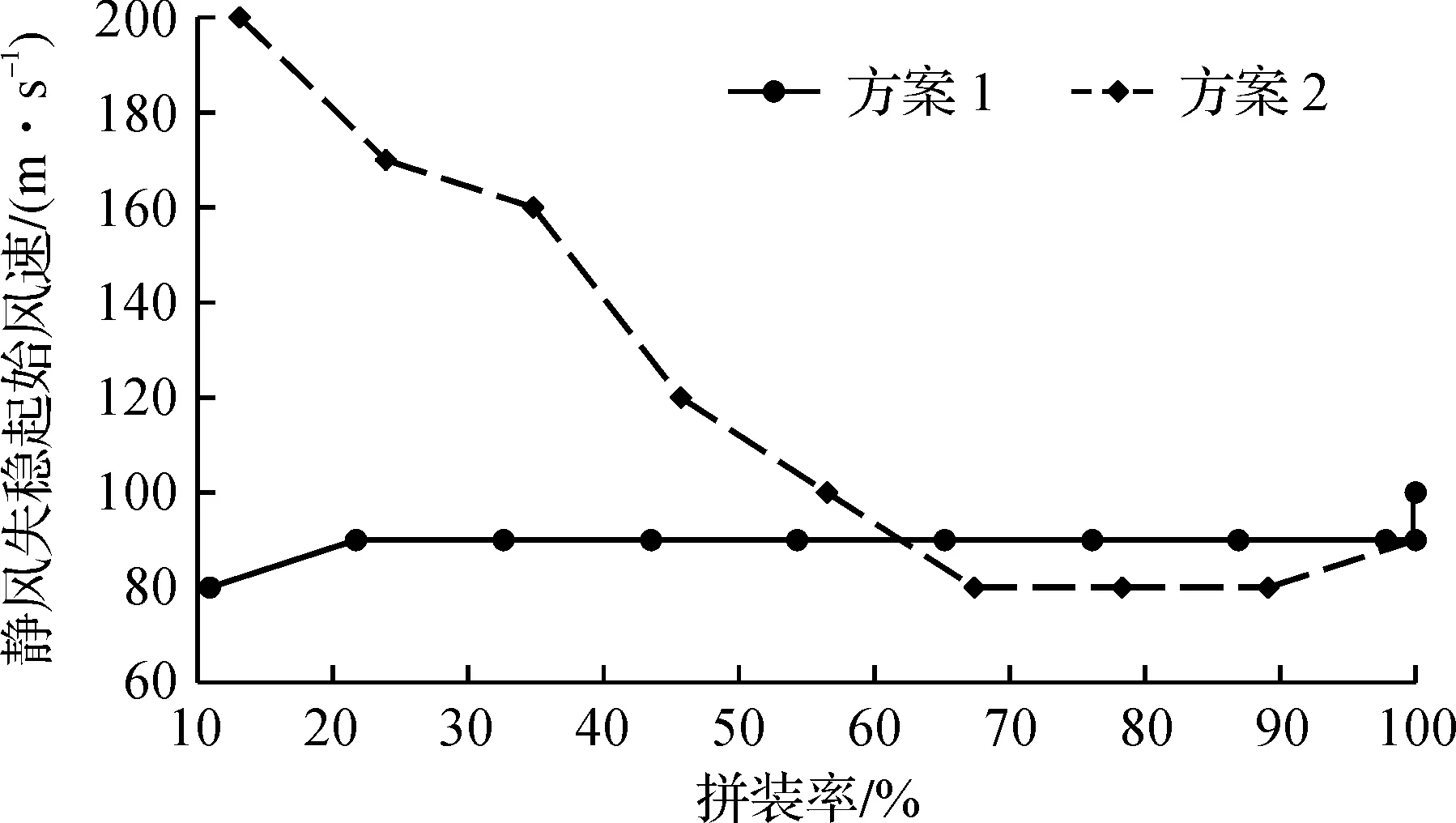
图9 施工过程静风失稳起始风速变化趋势Fig.9 Evolutions of the starting wind speed of aerostatic instability during construction

在0°初始风攻角下，基于上述两种主梁架设方案，采用SNAA程序进行施工全过程的静风稳定性分析，揭示施工全过程静风稳定性的变化规律，同时探明风速空间非均匀分布对大跨度悬索桥施工过程静风稳定性的影响。分析前，采用大跨度悬索桥施工状态分析程序(IASB)确定两种主梁架设方案各施工阶段的结构几何和内力状态，以此作为静风分析的基准态。根据上述成桥状态分析得知：风速沿竖向变化和风场分布宽度两个因素对悬索桥静风稳定性影响不大，施工过程静风稳定性分析则是在风场分布宽度为5L和考虑风速沿竖向变化情况下针对风速非对称分布因素进行。两种主梁架设方案的静风失稳起始风速随主梁拼装率的变化趋势如图9所示，风速非对称分布对两种主梁架设方案静风失稳起始风速的影响分别如表3，4所示。

表3 风速非对称分布对架设方案1施工过程静风失稳起始风速的影响

Table 3 Effect of wind speed asymmetrical distribution on the starting wind speed of aerostatic instability under deck erection sequence 1

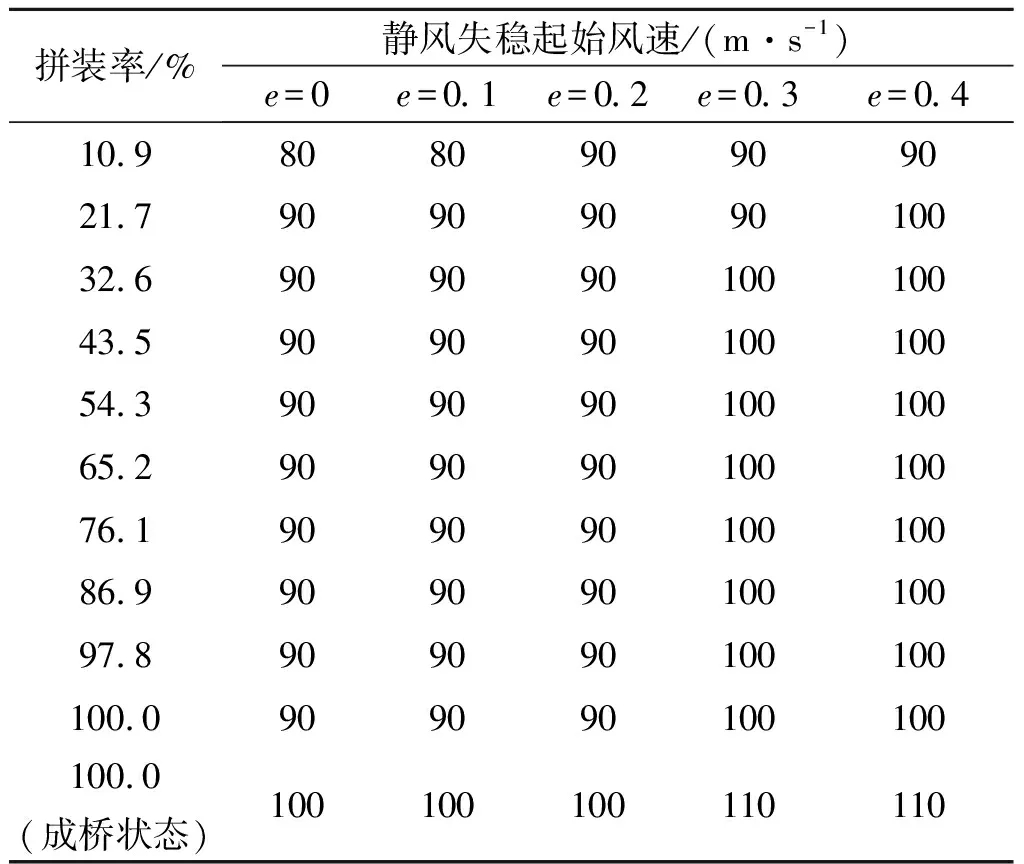
拼装率/%静风失稳起始风速/(m·s-1)e=0e=0.1e=0.2e=0.3e=0.410.9808090909021.79090909010032.690909010010043.590909010010054.390909010010065.290909010010076.190909010010086.990909010010097.8909090100100100.0909090100100100.0(成桥状态)100100100110110

观察图9可以看出：两种主梁架设顺序的静风失稳起始风速的变化趋势截然不同，主梁架设方案1施工过程结构的静风失稳起始风速变化非常平稳，在主梁架设初期结构的静风稳定性较低，随着主梁拼装长度的增加，静风失稳起始风速平稳上升，到成桥状态时达到最大值；与之相反，主梁架设方案2在主梁架设初期的静风失稳起始风速则非常高，结构具有很好的静风稳定性，但随着主梁拼装长度的增加，静风稳定性逐渐降低，在主梁拼装后期(拼装率60%～90%)其静风失稳起始风速略低于主梁架设方案1，合拢成桥后则与主梁架设方案1相同。总体而言，采用方案2的主梁架设顺序则更有利于悬索桥施工期的静风稳定性。

表4 风速非对称分布对架设方案2施工过程静风失稳起始风速的影响

Table 4 Effect of wind speed asymmetrical distribution on the starting wind speed of aerostatic instability under deck erection sequence 2

拼装率/%静风失稳起始风速/(m·s-1)e=0e=0.1e=0.2e=0.3e=0.413.1200200220240>24023.917017020021022034.816015015015016045.712011011012013056.5100909010010067.4808080909078.3808080809089.18080808090100.0909090100100100.0(成桥状态)100100100110110

从表3，4的结果比较可以得出：与成桥状态情况相类似，随着风速非对称程度的增加，施工过程结构静风失稳起始风速随之提高，风速非对称分布对施工过程结构的静风稳定性也有着明显的影响，同样需要在分析中准确考虑。

5 结 论

悬索桥加劲梁采用从两侧桥塔向跨中对称架设方案结构的静风稳定性要比从跨中向两侧桥塔对称架设方案好，尤其在主梁架设初期，因此从抗风稳定性角度考虑，悬索桥加劲梁宜采用从两侧桥塔向跨中对称拼装的施工顺序；风速沿竖向变化和风场分布宽度对悬索桥成桥和施工状态的结构静风稳定性影响不大，但风速非对称分布因素影响则比较显著，必要时需模拟实际地形在风洞中测试桥址处的风场分布系数，以准确预测结构的静风稳定性。