深度学习自编码结合混合蛙跳算法提取农田高光谱影像端元

韩立钦，张耀南，秦其明



深度学习自编码结合混合蛙跳算法提取农田高光谱影像端元

韩立钦1,2，张耀南1※，秦其明3

（1. 中国科学院西北生态环境资源研究院，兰州 730000；2. 中国科学院大学，北京 100049； 3. 北京大学地球与空间科学学院，北京 100871）

针对农田高光谱遥感影像端元提取和混合像元分解精度不高的问题，该文提出了利用深度学习自编码结合混合蛙跳算法的农田高光谱影像端元提取方法。首先，利用深度学习的栈式自编码模型对高光谱影像进行光谱特征提取，优选出备选端元集合；然后将影像端元提取问题转化为组合优化问题，设计了待优化的目标函数，通过混合蛙跳算法对目标函数进行优化从而实现对最佳端元组合的搜索；最后利用人工合成的不同信噪比农田高光谱数据和真实的农田高光谱影像，将该算法与3种现有的主要端元提取方法进行对比。试验结果表明，本文提出的端元提取算法对20 、30 和40 dB信噪比影像提取结果的平均光谱角分别达到0.106 88、0.030 32、0.009 94。对20 、30 和40 dB信噪比影像和真实影像提取结果的均方根误差分别达到0.050 8、0.015 9、0.005 1、0.006 7。与现有的主要端元提取方法相比，该方法具有端元提取精度高、对不同等级噪声鲁棒性好等优势，在农田高光谱遥感监测中具有广阔的应用前景。

作物；遥感；图像处理；高光谱；端元提取；栈式自编码；混合蛙跳算法

0 引 言

高光谱遥感为每个成像像元提供了很窄的成像波段和连续的反射光谱，在大面积的农作物种类识别、农作物产量估算、作物病虫害监测、自然资源调查等农业遥感的诸多领域有着广泛的应用前景[1-2]。但是，受限于传感器的信息获取能力，在保证一定信噪比的条件下，高光谱遥感影像的空间分辨率比较低。因此，对于高光谱影像而言，混合像元的问题尤为突出。为了更好地发挥高光谱遥感数据的优势，在对高光谱影像进行应用研究的过程中就需要进行混合像元分解[3]。因此现有的大多数混合像元分解的方法分为2个步骤：一是端元提取；二是端元丰度估算[4]。

在过去的几十年中，学者们提出了很多高光谱影像的端元提取方法。目前被广泛讨论和应用的算法主要有：纯像元指数法[5]，光学实时自适应光谱识别系统[6]，内部最大体积法[7]，迭代误差分析法[8]，凸锥分析[9]，自动形态学端元提取[10]，顺序最大角凸锥法[11]，迭代约束端元法[12]，个体进化策略法[13]，顶点成分分析法[14]，独立成分分析法[15]等。近年来，端元提取始终是高光谱遥感领域研究的热点问题之一，一些新的方法也不断涌现，如文献[16-17]。

虽然一系列的端元提取方法被提出，但是这些方法各有特色[18]。主要有：大多数算法基于凸面单形体的假设，如内部最大体积法（N-FINDR）、顶点成分分析法（vertex component analysis，VCA）等，但是由于线性混合模型的局限性以及传感器噪声的影响，端元并不一定位于凸面单形体的顶点，即直接把凸面单形体的顶点提取作为端元往往不能够把真正的端元正确提取出来；一些方法属于半自动方法，如PPI（pixel purity index，PPI）方法等，需要较多的人机交互式操作，受人为因素影响比较严重；大多数算法缺乏反馈机制，在顺序提取端元的过程中，最先被提取的端元对最终结果影响较大，并且容易导致算法陷入局部最优解。

端元提取的目的是为混合像元分解提供端元。事实上，由于地表的复杂性和传感器成像能力的有限性，高光谱影像的端元一般指影像中包含某种地物类型比例很高的像元，而不是仅仅包含一种地物的严格意义上的纯净像元[4]。为了更好地实现混合像元分解，端元提取可转化为一个离散优化问题：从影像中选取最佳端元组合，使得混合像元分解的精度达到最高。作为深度学习中的典型模型，栈式自编码（stacked autoencoder，SAE）能够以无监督的方式，通过逐层训练实现对高维信号的降维，相比主成分分析等传统方法优势明显[19-20]，是深度学习（deep learning，DL）的算法之一，为高光谱影像的特征提取提供了很好的技术支撑。混合蛙跳算法（shuffled frog leaping algorithm，SFLA）模拟了青蛙群体觅食行为过程中信息共享机制，是一个全新的启发式群体智能优化算法，具有优秀的计算性能和很好的全局搜索能力[21-22]。

针对上述端元提取方法的不足，本文提出一种基于深度学习中栈式自编码模型和混合蛙跳算法的农田影像端元提取方法。首先，利用SAE模型对高光谱影像进行特征提取，筛选出可用于混合像元分解的备用端元；然后利用SFLA算法对端元组合进行搜索和优化，得到能够使得混合像元分解精度最高的端元组合，为农田高光谱影像混合像元分解提供端元。

1 基于栈式自编码的光谱特征提取

本文算法流程如图1所示。为了将SAE和SFLA算法运用到农田影像端元提取中，对SAE和SFLA算法做了必要的适应端元提取问题的改进，重新定义了SAE和SFLA算法中的参数，设计了待优化的目标函数。

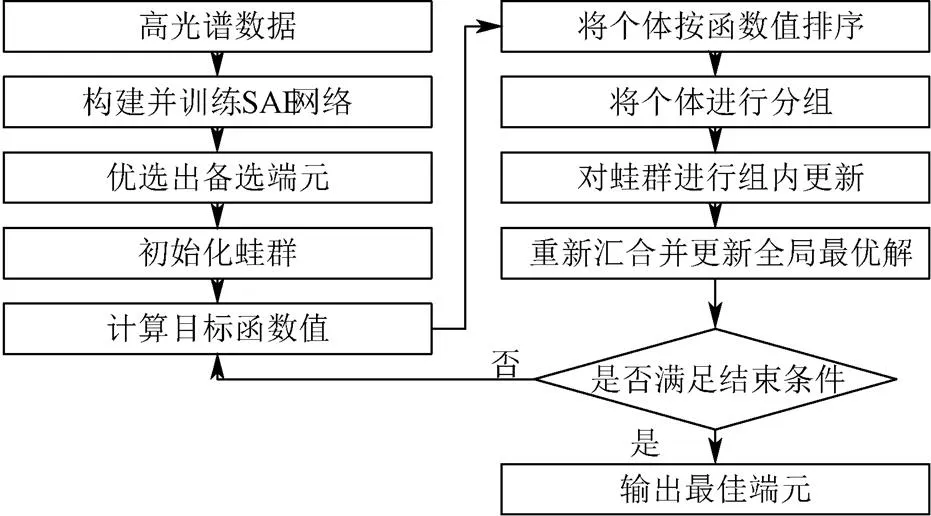
图1 深度学习结合混合蛙跳的农田高光谱影像端元提取流程

1.1 栈式自编码模型

在自编码神经网络中，每一层可以看作是对上层输出的非线性变换和特征表示，每增加一个隐含层就可以计算出更为复杂的特征表示[23]，所以利用深层的神经网络能够以更紧凑的方式来表达更多的函数集合，具备更好的特征提取能力。作为一种典型的深度学习模型，SAE模型由多个稀疏自编码神经网络串联组成，前一个自编码神经网络的输出层作为后一个自编码神经网络的输入层，每一层都是对输入层一种特征表示，尽可能地复现输入层的信息，从而实现特征提取。一个简单的SAE模型的结构如图2所示（以4层结构为例）。

对SAE神经网络的训练可以分成2个步骤：

1）使用逐层贪婪训练的方式对神经网络进行构建。利用输入层训练SAE的第一个自编码器；在保持第一个自编码器的参数不变的条件下，将第一个自编码器的输出层作为下一个自编码器的输入层，对第二个自编码器进行训练得到相应的权重和偏置量，如此类推，最终得到最后一个自编码器的权重、偏置量和输出层。

2）使用微调的方式对构建的神经网络进行优化。微调是深度学习中用于提高神经网络性能的典型策略。利用全局微调的方式，将由所有层构成的整个SAE神经网络看做一个整体，基于误差反向传播的方法对神经网络中的参数进行统一的修正。

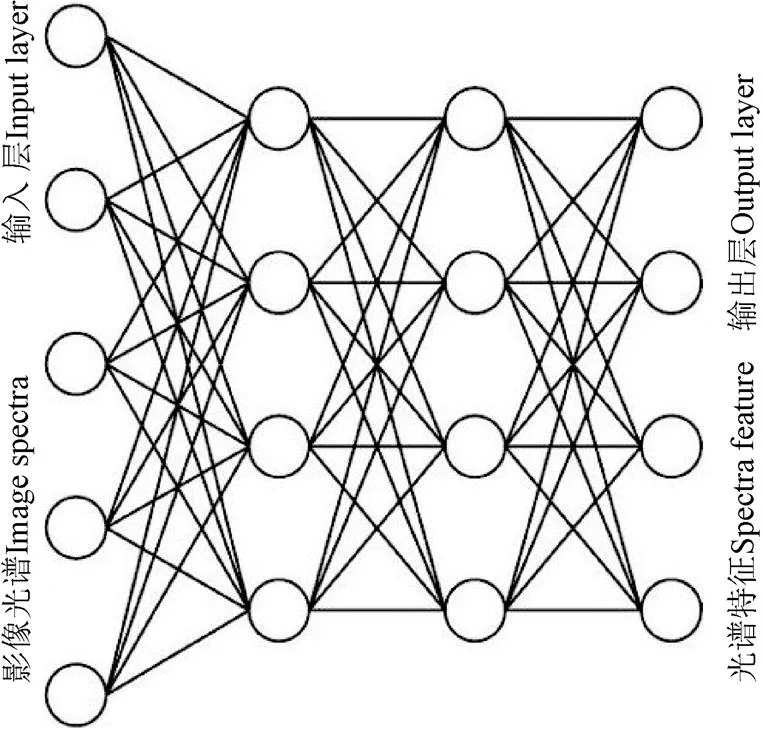
图2 4层栈式自编码神经网络模型的结构

1.2 光谱特征提取和备用端元优选

将该影像的每个像元视作一个训练样本，像元的波段数是SAE输入层的维数，每个波段的反射率值都是输入层的一个特征。构建SAE神经网络对影像像元进行特征提取，得到每个像元的特征表示。特征提取后的第个像元都可以表示为一个向量p= (p1, p2, p3, …, p)，123。其中为特征数，为影像的像元个数。将所有像元投放在维特征空间中，选择维几何体的端点及端点附近的像元作为备选端元。

2 基于混合蛙跳算法的端元搜索

2.1 目标函数设计

在混合蛙跳算法中，定义每一只青蛙的位置为端元提取解空间中一个解x(x1, x2, x3,…, x, …, x)，x1+x2+x3++x=m，x∈{0, 1}，其中为需要提取的端元个数，为备选端元的个数，x=1表示在第只青蛙代表的端元提取解中第个备选端元被选为端元。

在线性光谱混合模型中，端元丰度服从式（1）～（3）。

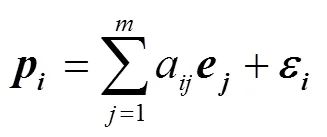
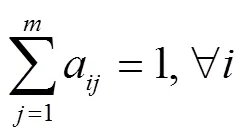
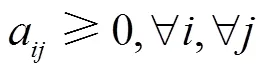
其中a（1, 2, 3,1, 2, 3,）表示第个端元在第个像元中所占的比例（端元丰度）；e（1, 2, 3,）为第个端元。采用经典的全约束条件下最小二乘法对上述线性混合模型进行混合像元分解[24]，得到端元丰度，再依据式（4）求得反混图像。

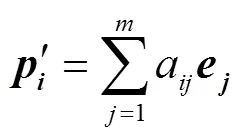
式中表示反混图像中第个像元反射率向量。端元提取的目的是得到高精度的混合像元分解的结果。本文采用混合像元分解后反混图像与原图像之间的均方根误差（root mean square error，RMSE）作为待优化的目标函数。RMSE在统计学中能够很好地反映出计算值与真实值的偏差，在端元提取的同类研究中被广泛用于评价端元提取的效果，如文献[17-18,25]。具体来说，对于第只青蛙，用于评价其位置优劣性的目标函数如式（5）。

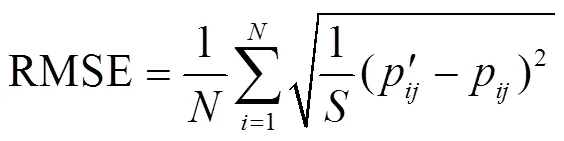
其中p表示原图像第个像元的第个波段的反射率。ʹ表示反混图像中第个像元的第个波段的反射率，是总波段数目。RMSE越小，说明该青蛙位置越好，其代表的端元组合越接近于最佳端元组合。

2.2 蛙群更新与端元搜索

对蛙群的参数（青蛙数目、分组数目、组内进化次数、青蛙允许移动的最大距离D和最大迭代次数）进行初始化，然后按照如下步骤进行蛙群更新与端元搜索（可参见图1）。

1）蛙群分组：对每只青蛙随机初始化以后，计算每只青蛙对应的RMSE值，将青蛙按照RMSE值升序进行排列，并将种群分为个组：排序完成后，第1只青蛙进入第1组，第2只青蛙进入第2组，直到第只青蛙进入第组，然后第+1只青蛙再进入第1组，以此类推，直到所有青蛙分组完毕。

2）组内更新：对组内位置最差（RMSE值最大）的青蛙按式（6）～式（7）进行位置更新。

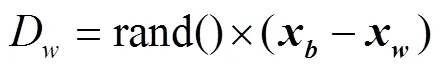
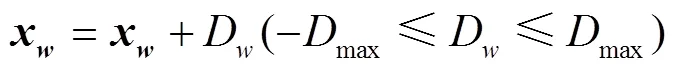
其中x表示组内位置最好的青蛙，x表示组内位置最差的青蛙，rand()是0～1之间随机生成的数。如果最差青蛙经过更新后位置能够变好，则用新位置的青蛙代替原来位置的青蛙，否则用整个种群中最好的青蛙x代替x，然后再次执行式（6）～式（7）。每次执行式（6）～式 （7）完毕以后，按照值的大小顺序，取x矢量的前个分量赋值为1，用于代表个被提取出来的端元，其余值赋值为0。如果仍然不能得到更好的位置或者移动距离超过D，则随机产生一个青蛙的位置替代x。

3）整体更新：对每组的青蛙完成更新以后，将所有青蛙重新混合，更新全局最佳位置的青蛙，判断是否满足终止条件（达到最大迭代次数或者全局最佳位置在连续3次迭代中重复），如果满足条件则结束迭代，全局最佳位置的青蛙所代表的端元组合即为最终提取到的端元，如果不满足迭代条件，则重新进行蛙群分组、组内更新、整体更新。

本文算法与现有的主要端元提取算法[17]的时间复杂度对比见表1。由于影像像元个数远远大于影像降维以后的维数和青蛙数，所以时间复杂度主要取决于影像像元个数。此外，青蛙数小于影像降维以后的维数。所以，由表1可知，本文算法的时间复杂度与现有的端元提取算法相当，并略有降低。

表1 不同算法的时间复杂度对比

注：()代表时间复杂度；表示迭代循环次数，17～24；为影像像元个数；为影像降维以后的维数；为青蛙数；＝2.3～2.9[14]。

Note:() represents the time complexity.represents the number of iteration cycles,=17-24.is the number of image pixels.is the dimension after image dimensionality reduction.is the number of frogs.=2.3-2.9[14].

3 验证试验与结果分析

分别采用合成的农田高光谱数据集和真实的农田航空高光谱遥感影像对3种典型的端元提取方法的结果进行计算，包括SMACC（顺序最大角凸锥法，sequential maximum angle convex cone，SMACC）、VCA算法、N-FINDR算法，并与本文算法结果进行对比。验证方案（包括数据获取和验证方法）采用国内外研究高光谱影像端元提取的通用方案[26-28]。

3.1 人工合成农田高光谱数据验证

采用人工合成高光谱数据进行算法的验证是国际上该方面研究的通用做法[27,29-30]，本文采用大多数研究数据合成方法，从美国地质调查局（USGS）标准光谱库、美国约翰霍普金斯大学标准光谱库、Chris Elvidge标准光谱库中随机选取5种地物（灌木植被、草、砂壤土、粉质壤土、细砂壤土）的光谱作为端元光谱（如图3所示），并重采样为224个波段模拟农田高光谱影像光谱，利用如下方法合成高光谱数据：建立64×64大小的空白图像矩阵，在每一个位置随机选取一种地物类型，并赋予其对应的光谱；将图像矩阵划分为8×8的方块区域，每个区域包含8×8个像元；对图像施加9×9的均值滤波器实现像元混合[27,29-30]；利用式（8）对图像分别施加信噪比SNR（signal to noise ratio）分别为20、30和40 dB的服从标准正态分布的高斯噪声，得到3个信噪比不同的高光谱数据，如图4所示。

SNR=lg(E[T]/ E[T]) （8）

其中为原始信号光谱，为噪声光谱，E表示数学期望运算，T表示矩阵转置运算。本文端元提取的结果利用如下2个指标进行衡量：

1）最终提取出来的端元与光谱库中标准光谱之间的光谱角，如式（9）所示。

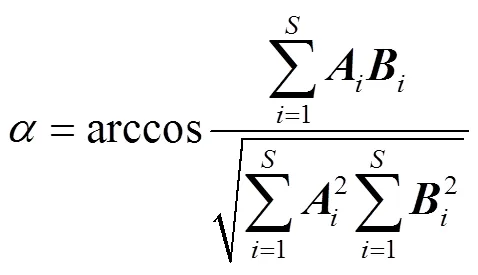
其中、分别为待评价的端元光谱和标准光谱向量，是总波段数目。光谱角衡量了2个光谱之间形状的相似性，忽略光谱数值的大小，即与光谱向量的模无关，而与光谱曲线的起伏形状密切相关，而光谱曲线的形状由地物类型决定，光谱角越小，说明提取的端元地物类型越接近真实端元地物类型。

2）端元提取后进行混合分解得到端元丰度，再按照式（4）计算反混图像，然后计算式（5）中的RMSE值对端元提取结果进行评价。RMSE衡量2个光谱之间的对应波长处数值的相似性，是对光谱形状和反射率大小相似性的整体评价。RMSE越小，说明提取的端元光谱在数值上越接近真实端元。

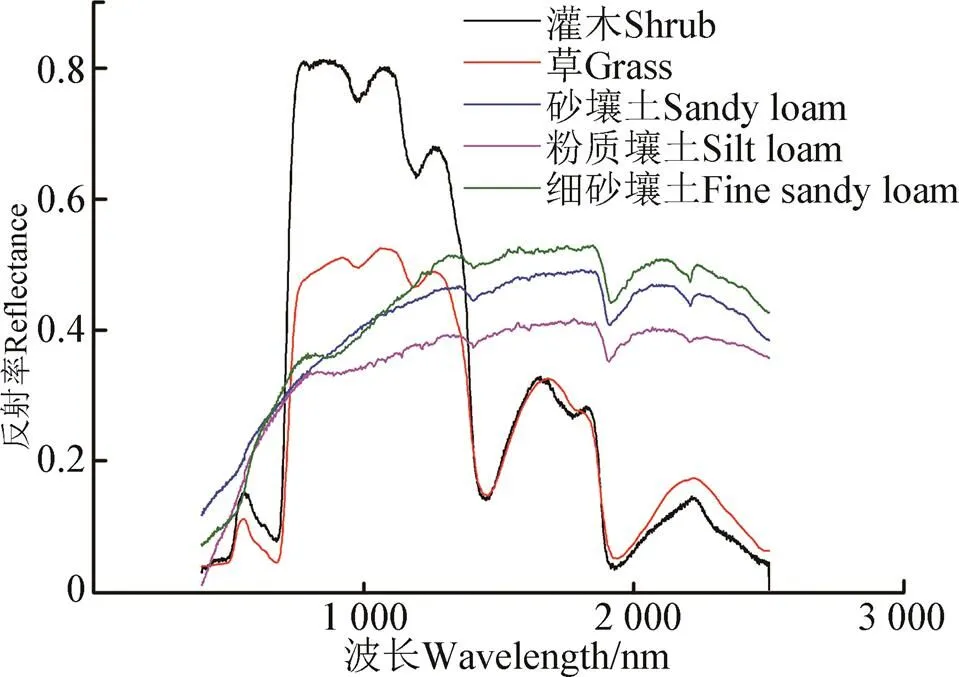
图3 用于合成高光谱数据的5种端元光谱

a. SNR=20 dBb. SNR=30 dBc. SNR=40 dB

4种方法对不同信噪比的人工合成高光谱数据得到的光谱角如表2所示，得到的RMSE值如表3所示。以SNR=30 dB的影像为示例，提取到的端元光谱如图 5所示。在人工合成农田高光谱数据的试验中，不同信噪比的数据都出现了相似的结果，本文算法相比现有方法得到的端元与标准光谱之间的光谱角最小，平均光谱角分别为0.106 88（20 dB）、0.030 32（30 dB）、0.009 94（40 dB）（值得注意的是，N-FINDR算法只提取到4种端元），利用本文算法提取到的端元进行混合像元分解，其反混图像与原始图像之间的RMSE也是最小，分别为0.050 8、0.015 9、0.005 1。通过图3和图5的光谱对比可以发现，本文算法提取的端元曲线更接近用于合成数据的原始端元曲线，即本文算法提取的端元质量比其他算法显著改善。对不同的噪声水平，本文算法都能够正确提取端元，说明本文算法对数据噪声的鲁棒性好。

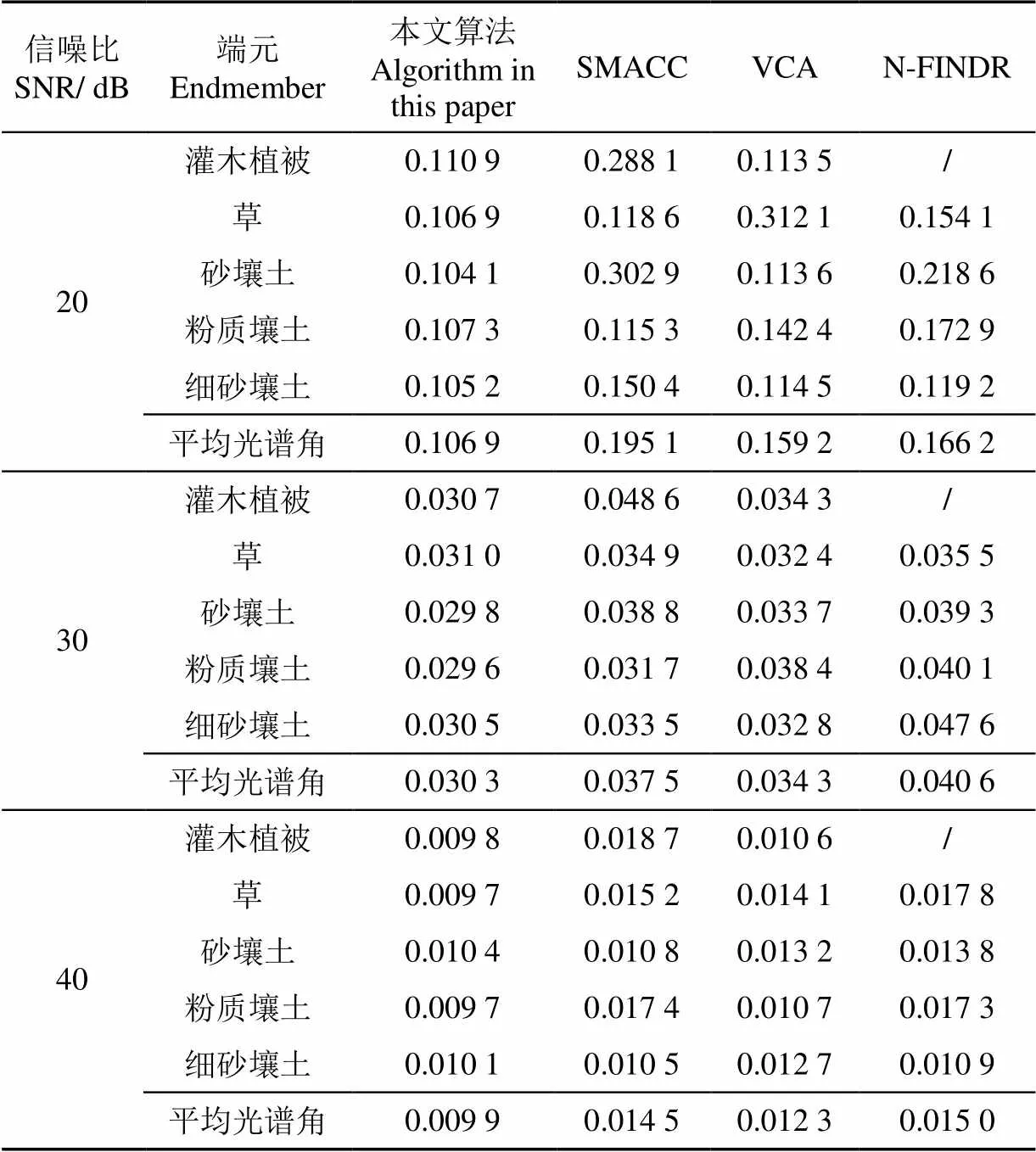
表2 不同信噪比的合成高光谱数据试验的光谱角

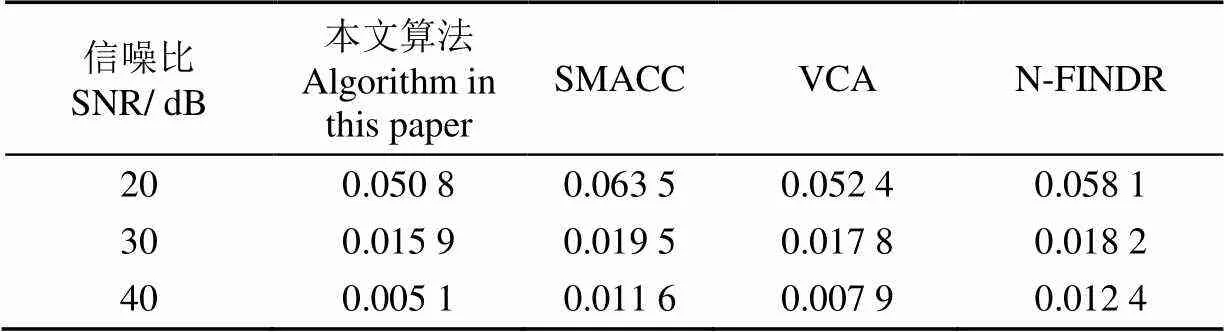
表3 不同信噪比的合成高光谱数据试验的RMSE值

3.2 真实高光谱影像验证

对真实的高光谱影像目前无法获取其真正的端元光谱作为参考，因此无法对端元光谱直接进行比较，目前国际同类研究均直接给出反混图像的RMSE，并与其他方法进行对比[26-28]，本文也采用这种方法。真实高光谱影像验证选用Salinas高光谱影像。Salinas高光谱影像由AVIRIS传感器获取，覆盖了美国加利福尼亚州Salinas地区，包含224个光谱波段，其成像时间为1992年，是国际上公认的公共测试数据，广泛用于高光谱影像数据处理方法的验证。本文选用Salinas影像的一个空间子集，称为Salinas-A图像（如图6，该子集是国际通用标准数据集），包含6种植被端元类型（1种椰菜端元、1种玉米端元和4种生菜端元），该子集被广泛应用于高光谱遥感相关算法的测试[26-28]。对于真实高光谱影像很难确定标准光谱进行端元的评价，目前国际上也没有该影像的标准端元光谱。对于端元提取后混合像元分解的RMSE值，4种算法（本文算法、SMACC、VCA、N-FINDR）的RMSE分别为0.006 7、0.008 5、0.007 4、0.009 2。对真实高光谱数据而言，利用本文算法提取的端元进行混合像元分解，反混图像与原始图像的RMSE值最小（0.006 7）。本文算法对人工合成数据和真实数据的验证结果相似，说明本文算法相比现有主要算法的端元提取精度更高。

本文提出的端元提取方法主要分为2大步骤，第一步是利用深度学习选择备选端元，第二步是将优选出来的端元输入混合蛙跳算法得到最佳的端元组合。在第一步目的是降低第二步计算的复杂性，目前常用的方法是主成分分析、最小噪声分离等，深度学习比起目前方法来说选择备选端元更加精准，同等情况下给第二步提供的备选端元数量少，减小第二步的运算量。第二步是端元提取算法的关键，算法的优劣直接决定了最终提取的端元精度。因此，深度学习的贡献主要在于降低第二步计算的复杂性，而第二步对端元提取具有决定性贡献，第二步骤的贡献大于第一步骤。

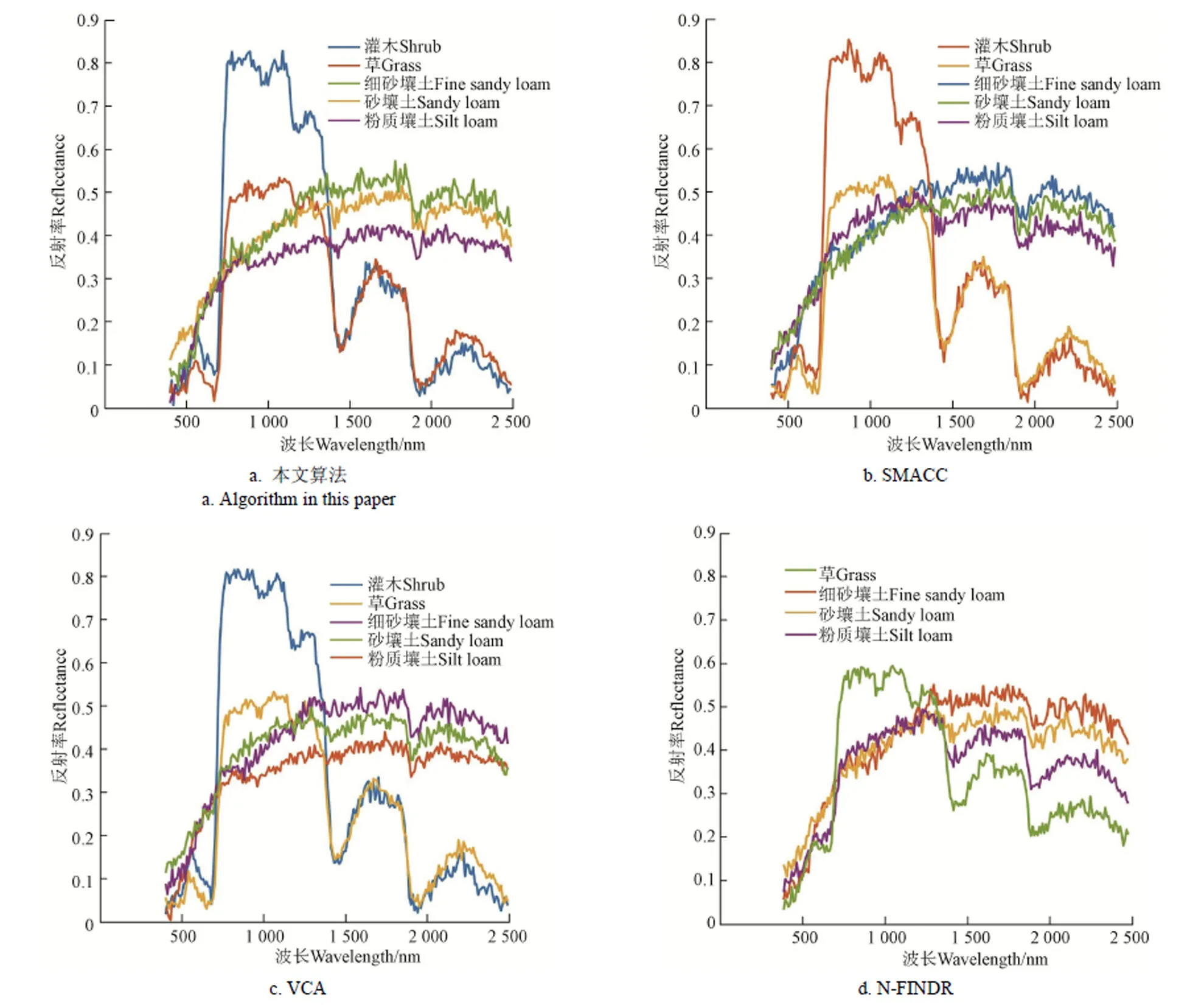
图5 不同算法的合成高光谱影像端元光谱提取结果（SNR=30 dB）

图6 Salinas-A图像的灰度图像

4 结 论

针对高光谱遥感混合像元分解的问题，本文提出了基于深度学习中栈式自编码和混合蛙跳算法的端元提取方法。利用人工合成的农田高光谱数据和真实的AVIRIS高光谱影像数据对本文算法进行了试验验证，并与现有的主要高光谱影像端元提取算法进行对比。结果表明：

1）本文算法对人工合成数据提取到了更高精度的端元光谱，平均光谱角分别达到0.106 88（20 dB）、0.030 32（30 dB）、0.009 94（40 dB），对20 、30 、40 dB信噪比影像提取结果的均方根误差分别达到0.050 8、0.015 9、0.005 1，均优于现有算法。本文算法在不同水平的数据噪声下性能稳定，在不同信噪比条件均能取得优于其他算法的结果，算法鲁棒性好。

2）对于真实高光谱影像，本文算法能够提高农田高光谱遥感影像端元的提取精度，反混图像与原始图像的均方根误差达到0.006 7，优化了混合像元分解的结果。

本文算法在农业遥感应用过程中具有广阔的发展前景。在未来的研究中，可用更多的农田高光谱影像对算法进行验证。

[1] Wu M, Huang W, Niu Z, et al. Fine crop mapping by combining high spectral and high spatial resolution remote sensing data in complex heterogeneous areas[J]. Computers and Electronics in Agriculture, 2017, 139(6): 1－9.

[2] 杨红卫，童小华. 中高分辨率遥感影像在农业中的应用现状[J]. 农业工程学报，2012，28(24)：138－149. Yang Hongwei, Tong Xiaohua. Application status of middle and high resolution remote sensing images in agriculture[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(24): 138－149. (in Chinese with English abstract)

[3] 蓝金辉，邹金霖，郝彦爽，等. 高光谱遥感影像混合像元分解研究进展[J]. 遥感学报，2018，22(1)：13－27． Lan Jinhui, Zou Jinlin, Hao Yanshuang, et al. Research progress on ummixing of hyperspectral remote sensing imagery[J]. Journal of Remote Sensing, 2018, 22(1): 13－27. (in Chinese with English abstract)

[4] 张成业，秦其明，陈理，等. 高光谱遥感岩矿识别的研究进展[J]. 光学精密工程，2015，23(8)：2407－2418. Zhang Chengye, Qin Qiming, Chen Li, et al. Research and development of mineral identification utilizing hyperspectral remote sensing[J]. Optics and Precision Engineering, 2015, 23(8): 2407－2418. (in Chinese with English abstract)

[5] Graceline Jasmine S, Pattabiraman V. Performance analysis of statistical-based pixel purity index algorithms for endmember extraction in hyperspectral imagery[J]. Advances in Intelligent Systems and Computing. 2018(645): 10－21.

[6] Peter D B H, Wang X. Spectral representation of proton nmr spectroscopy for the pattern recognition of complex materials[J]. Journal of Analysis and Testing, 2017, 1(2): 1－10.

[7] 王红军，熊俊涛，黎邹邹，等. 基于机器视觉图像特征参数的马铃薯质量和形状分级方法[J]. 农业工程学报，2016，32(8)：272－277. Wang Hongjun, Xiong Juntao, Li Zouzou, et al. Potato grading method of weight and shape based on imaging characteristics parameters in machine vision system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(8): 272－277 (in Chinese with English abstract).

[8] Zhang C, Qin Q, Zhang T, et al. Endmember extraction from hyperspectral image based on discrete firefly algorithm (EE-DFA)[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 126(4): 108－119.

[9] Makeev V V. Dividing a convex figure by a system of rays and inscribed polygons[J]. Mathematics, 2015, 48(3): 366－375.

[10] Plaza A, Plaza J, Martin G. Spatial-spectral endmember extraction from hyperspectral imagery using multi-band morphology and volume optimization[C]. IEEE International Conference on Image Processing, 2009(1): 3721－3724.

[11] Gruninger J H, Ratkowski A J, Hoke M L. The sequential maximum angle convex cone (SMACC) endmember model[J]. Proceedings of Spie, 2004, 5425(8): 1－14.

[12] Berman M, Kiiveri H, Lagerstrom R, et al. ICE: a statistical approach to identifying endmembers in hyperspectral images[J]. IEEE Transactions on Geoscience & Remote Sensing, 2008, 42(10): 2085－2095.

[13] Manuel A, Hernandez C, Gallego J. A single individual evolutionary strategy for endmember search in hyperspectral images[J]. Information Sciences, 2004, 161(3–4): 181－197.

[14] Nascimento J M P, Dias J M B. Vertex component analysis: A fast algorithm to unmix hyperspectral data[J]. IEEE Transactions on Geoscience & Remote Sensing, 2005, 43(4): 898－910.

[15] 李宏俏. 高光谱图像的光谱解混模型与算法研究[D]. 成都：电子科技大学，2017. Li Hongqiao. Study of Unmixing Models and Algorithms for Hyperspectral Images[D]. Chengdu: University of Electronic Science and Technology of China, 2017. (in Chinese with English abstract)

[16] 金瑞，李小昱，颜伊芸，等. 基于高光谱图像和光谱信息融合的马铃薯多指标检测方法[J].农业工程学报，2015，31(16)：258－263. Jin Rui, Li Xiaoyu, Yan Yiyun, et al. Detection method of multi-target recognition of potato based on fusion of hyperspectral imaging and spectral information[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(16): 258－263. (in Chinese with English abstract)

[17] Xu Mingming, Zhang Liangpei, Du Bo, et al. An image-based endmember bundle extraction algorithm using reconstruction

error for hyperspectral imagery[J]. Neurocomputing, 2016, 173(2): 397－405.

[18] Zhang B, Sun X, Gao L, et al. Endmember extraction of hyperspectral remote sensing images based on the ant colony optimization (ACO) algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4173－4176.

[19] Chen Y, Lin Z, Zhao X, et al. Deep learning-based classification of hyperspectral data[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2014, 7(6): 2094－2107.

[20] Bengio Y, Lamblin P, Popovici D, et al. Greedy layer-wise training of deep networks[J]. Advances in Neural Information Processing Systems, 2007, 19(1): 153－160.

[21] Eusuff M M, Lansey K E. Optimization of water distribution network design using the shuffled frog leaping algorithm[J]. Journal of Water Resources Planning and Management, 2003, 129(3): 210－225.

[22] Daoden K, Thaiupthump T. A Modified Shuffled Frog Leaping Algorithm Using Truncated Gaussian Distribution in Frog’s Position Updating Process[J]. Information Science and Applications (ICISA), 2016, 376(2): 965－974

[23] 崔广新，李殿奎. 基于自编码算法的深度学习综述[J]. 计算机系统应用，2018，27(9)：47－51. Cui Guangxin, Li Diankui. Overview on deep learning based on automatic encoder algorithms[J]. Computer Systems & Applications, 2018, 27(9): 47−51. (in Chinese with English abstract)

[24] Denisova A, Juravel Y, Myasnikov V. Linear spectral mixture analysis of hyperspectral images with atmospheric distortions[J]. Computer Vision and Graphics. 2016, 9972(9): 134－141

[25] Zhang B, Sun X, Gao L, et al. Endmember extraction of hyperspectral remote sensing images based on the discrete particle swarm optimization algorithm[J]. IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(11): 4173－4176.

[26] Filippi A M, Archibald R . Support vector machine-based endmember extraction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(3): 771－791.

[27] Miao L, Qi H. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(3): 765－777.

[28] Chan T H, Ambikapathi A M, Ma W K, et al. Robust affine set fitting and fast simplex volume max-min for hyperspectral endmember extraction[J]. IEEE Transactions on Geoscience & Remote Sensing, 2013, 51(7): 3982－3997.

[29] Rajabi R, Ghassemian H . Spectral unmixing of hyperspectral imagery using multilayer NMF[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 12(1): 38－42.

[30] Chang C I, Xiong W, Liu W, et al. Linear spectral mixture analysis based approaches to estimation of virtual dimensionality in hyperspectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(11): 3960－3979.

Endmember extraction of farmland hyperspectral image using deep learning autoencoder and shuffled frog leapingalgorithm

Han Liqin1,2, Zhang Yaonan1※, Qin Qiming3

(1.,,730000,; 2.,100049,; 3.,,100871,)

Hyperspectral remote sensing image includes hundreds of narrow contiguous spectral bands with high spectral resolution, and can provides a contiguous spectral curve for each pixel, which is an important tool for the cropland monitoring in rapid and large-scale way. However, due to the contradiction between spectral resolution and spatial resolution, hyperspectral remote sensing image usually possesses relative low spatial resolution. Therefore, it is very important to mix various vegetation and soil at one pixel point for spectral decomposition in hyperspectral image and spectral unmixing of farmland. The first step in spectral unmixing is usually endmember extraction. Endmember extraction from a hyperspectral remote sensing image is to find some pixels (endmembers) and regard them as pure spectral reflectance of the vegetation and soil in the image to get the best accuracy of spectral unmixing results. So endmember extraction from hyperspectral remote sensing image can be regarded as a typical discrete optimization problem, which can be solved by swarm intelligence optimization algorithm. Before optimization, the spectral dimension of the image should be reduced by deep learning. In order to solve the problem of spectral unmixing of hyperspectral images, a method of extracting farmland endmember based on deep learning and shuffled frog leaping algorithm (SFLA) is proposed in this paper. Firstly, deep learning model named stacked auto encoders (SAE) was used to extract spectral features . SAE performs a non-linear transfer from the original spectral signals to a form with significant features and less dimensions. In the low-dimension space, the candidate endmembers were selected as the input of the SFLA. The purpose of extracting the candidate endmembers is to simplified the computational complexity in the next step. Secondly, the endmember extraction of hyperspectral image was transferred into the combinatorial optimization and the objective function was constructed, then the SFLA was used to optimize the objective functionto get the best combination of endmembers. The objective function in study was designed as the RMSE (root mean square error) between the real hyperspectral remote sensing image and the simulated hyperspectral remote sensing image using the endmembers and abundance after endmember extraction and spectral unmixing. Thirdly, 2 groups experiments were carried out on the synthetic hyperspectral datasets with 3 different SNR (signal to noise ratio, 20 , 30 and 40 dB) and the real AVIRIS hyperspectral remote sensing dataset in Salinas region, respectively. In experiments, the experimental results of the proposed method was compared with that of 3 traditional methods for endmember extraction including the sequential maximum angle convex cone (SMACC), N-FINDR, Vertex Component Analysis (VCA). The results were evaluated by RMSE and spectral angle. The results showed that the RMSE was 0.050 8, 0.015 9, 0.005 1, 0.006 7 for 20, 30 and 40 dB dataset, and the real dataset, respectively. The average spectral angle was 0.106 88, 0.030 32, 0.009 94 for 20, 30 and 40 dB dataset respectively. The proposed method was better than traditional methods in terms of extraction accuracy, which had wide potential applications on cropland monitoring using hyperspectral remote sensing. The method proposed in this paper reduced the influence of the non-linear factors and the noise, better endmember extraction and spectral unmixing results (both less spectral angle and less RMSE) could be obtained, and the proposed method was robust when the noise of the image increased sharply. In conclusion, the endmember extraction method proposed by this study is of significant importance for the cropland monitoring using hyperspectral remote sensing and has a prosperous future for the application on the remote sensing of agriculture.

crops; remote sensing; image processing; hyperspectral; endmember extraction; stacked autoencoders; shuffled frog leaping algorithm

2018-11-29

2019-01-29

国家科技基础条件平台项目（Y719H71006）；中科院信息化专项（XXH13506）；甘肃省高校科技转化项目（2017D-27）

韩立钦，副教授，博士生，主要研究方向为定量遥感与地理信息集成。Email：hanliqin@lzb.ac.cn

张耀南，研究员，博士，主要研究方向为地学大数据融合分析。 Email：yaonan@lzb.ac.cn

10.11975/j.issn.1002-6819.2019.06.020

TP394.1；TH691.9

A

1002-6819(2019)-06-0167-07

韩立钦，张耀南，秦其明. 深度学习自编码结合混合蛙跳算法提取农田高光谱影像端元[J]. 农业工程学报，2019，35(6)：167－173. doi：10.11975/j.issn.1002-6819.2019.06.020 http://www.tcsae.org

Han Liqin, Zhang Yaonan, Qin Qiming. Endmember extraction of farmland hyperspectral image using deep learning autoencoder and shuffled frog leapingalgorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(6): 167－173. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.06.020 http://www.tcsae.org