利用三维激光扫描数据进行建筑物立面点云分割算法分析

贺亦峰,胡 荣,邹进贵

(1. 武汉大学测绘学院，湖北 武汉 430079； 2. 文华学院，湖北 武汉 430074)

随着“智慧城市”建设的普及，尤其是车载激光扫描技术的迅速发展与应用[1-3]，三维激光扫描技术已成为空间数据获取的一种重要技术手段[4]，但大场景的三维点云数据量大，人工处理数据效率低下[5]，如何快速高效地将大量的点云数据进行重建与识别成为关键问题。点云分割对于目标识别和特征重建有着直接的影响，是实现点云重建与识别的基础。

国内外学者提出了多种点云分割方法。一些学者利用RANSAC方法对建筑物表面点云进行提取[6]，并利用Delaunay三角网提取边界点云[7]，取得了较好的效果。还有一些学者对RANSAC点云分割方法进行改进，如文献[8]利用自适应性Hough变换对点云进行分割，能高效分割采集的点云。一些学者利用平面增长算法分割点云，如文献[9]利用了数据的相似性，这种算法受到种子平面的限制。文献[10]提出了一种多样性的区域增长算法，利用一种不规则三角网描述平面的基本特征，通过比较相邻三角形的关系式去融合三角形。文献[11]根据平面增长算法提出了一种自动提取分割平面的算法，在这种方法中结果受参数影响较大。

点云分割如何在精度和速度间找到平衡是一个重要的问题。本文使用多种经典分割方法进行点云分割并比较分割精度、效率及适用范围，在此基础上提出一种新的分割方法，在建筑物立面点云分割上取得较好的效果。

1 三维激光点云立面分割算法

点云分割是将属于同一平面的点云分割出来。目前常见的点云分割方法有：基于欧氏聚类的点云分割算法、基于区域增长的点云分割算法、基于RANSAC的点云分割算法。在这几种算法基础上，本文提出一种结合RANSAC和欧氏聚类的点云分割算法，并在试验过程中取得了较好的分割效果。

1.1 基于欧氏聚类的点云分割

欧氏聚类方法是以欧氏距离为参考依据进行聚类的一种方法[12]，它利用KD-tree对点云进行分割，欧氏空间中的一个3D平面：Ax+By+Cz+D=0。在点云集合中取点Pi(xi,yi,zi)，则Pi到该平面的距离可以表示为

(1)

1.2 基于区域增长的点云分割

区域增长算法将每一块区域作为处理对象，主要参考区域内和区域间的异同关系，能够较好地区分出图像中的区域边界。区域增长算法的基本思想是将具有相似性质的点云集中起来构成区域，该方法需要先选择一个种子点，然后依次将种子点云周围的相似点合并到种子点云所属的区域中[13]。

1.3 基于RANSAC算法的点云分割

随机抽样一致性(random sample consensus，RANSAC)于1981年由Fischler和Bolles最先提出[14]。它是一种稳健的模型参数估计算法，可根据一组包含异常数据的样本数据集计算出数据的数学模型参数，得到有效的样本数据[15]。

当点云中的误差点数为Nn，不正常的点数为Ne时，n全部是不正常的点的情况为

(2)

为了在三维激光点云中选择合适的点必须提高迭代的次数，当最小的选取点数为n时，取得良好的抽样子集的概率P应满足

P=1-(1-εk)n

(3)

式中，ε为没有误差的点在总的点云数中的比值；k为模型参数解算过程中所需要的最小的数据；P的取值范围在0.9～0.99之间。因此可以得到

(4)

判断迭代是否继续进行的条件为：①在当前迭代的点数多于最佳拟合平面的点数时，将最佳拟合平面的点替换为当前点；②在当前点数量与最佳拟合平面点数量相同且当前点阈值较小时，将最佳拟合平面的点替换为当前点。

1.4 RANSAC与欧氏聚类结合的点云分割

基于欧氏聚类的点云分割得到的分割主要是由点到分割面的阈值d0作为判断依据的，当阈值较大时会呈现一大片点云为一个分割面，而当减小分割阈值后，虽可以将明显的分割面分离开来，但又极易将同一层面的点云分成多类点云。与基于欧氏聚类的点云分割算法相比，基于RANSAC的点云分割效果可控因素较多，通过设置合适的阈值可以较好地分割建筑物立面点云，但该算法也存在部分误分割现象，且不能将每块窗户分割开来。

因此，本文提出一种结合RANSAC与欧氏聚类的点云分割算法。首先使用RANSAC算法对点云进行粗分割，得到大面积的点云立面，即墙面和窗沿，而对于剩下的点云数据，利用欧氏聚类算法进行分类，设置较大的欧氏距离阈值，可以较好分割出窗户元素。该算法的流程如图1所示。

图1 结合RANSAC与欧氏聚类的点云分割流程

2 试验与分析

扫描建筑物立面得到原始的三维激光点云数据(如图2所示)，为了提高后期分割的效率，需要提前对原始数据作预处理。首先剔除干扰点云，原始点云数据总量为658 023，经过点云剔除后剩余点云数量为251 109(如图3所示)。数据剔除以后点云整体效果更整齐，更便于分割处理。随后对经过剔除以后的点云数据滤波去噪，去噪后点云数量为71 343(如图4所示)。

图2 原始点云数据

图3 点云剔除后点云数据

图4 滤波去噪后点云数据

点云数据预处理后采用基于欧氏聚类的点云分割、基于区域增长的点云分割、基于RANSAC的点云分割、结合RANSAC和欧氏聚类的点云分割4种算法对预处理后的点云数据进行分割，通过C++编程实现点云分割。其中，基于欧氏聚类的算法在点到聚类面的距离的阈值选择上很难取到一个能直接将窗户、墙面、窗沿等区分开的值。而RANSAC算法进行点云分割可以通过类似于深度值的参数较好地分割窗户、墙面、窗沿，但无法将窗户之间分割开来，且存在大量点云未被处理。由此提出一种新的点云分割算法，首先用RANSAC算法粗分割点云，再用欧氏聚类方法分割独立的窗户元素。

对上述几种点云分割算法进行多次试验，试验平台为Windows10 64位系统，主要硬件配置为Intel core i7-4720HQ，12 GB内存。设置不同阈值，统计各种算法的精度和运行耗时。

2.1 基于欧氏聚类的点云分割算法

基于欧氏聚类的点云分割结果主要由点到聚类面的距离阈值决定，设置该距离阈值分别为7、8、9、10 cm，每一个距离测试两次(分别让最小点云数量为50和100)，统计试验用时、未分割个数和过分割个数，如图5—图7所示。

图5 欧氏聚类点云分割运行耗时统计

图6 欧氏聚类点云分割未分割个数统计

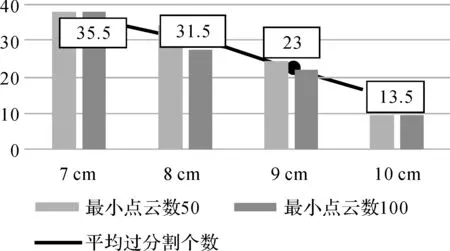
图7 欧氏聚类点云分割过分割个数统计

当阈值增大时，程序运行时间缓慢增加。精度方面，未分割数量会显著增加，过分割个数随着阈值增加而较少，这是由聚类数量减少导致。由分析结果可以看出，很难控制欧氏距离的阈值得到理想的分割结果，该分割方法只有当待测物为分离较远的几个独立物体才适合使用。距离阈值为7和10 cm时的分割结果分别如图8、图9所示。

图8 欧氏聚类(阈值7 cm)

图9 欧氏聚类(阈值10 cm)

2.2 基于区域增长的点云分割

本试验设置平面包含的最小点数为50，设置法向量估计中最邻近点数为50、40、30、20、10，设置参考邻域点数为5、10、15、20、30，设置法线夹角阈值为3°、5°、7°、10°、15°。默认参数为：法线估计最邻近点30，参考邻域点15，法线夹角阈值7°。该算法若不将点云先进行滤波处理，区域增长算法处理噪声很慢，运行时间会达到30 min以上，故在分割前进行滤波处理去除噪声。统计不同参数下的运行耗时、未分割个数和过分割个数见表1。

表1 基于区域增长的点云分割不同参数下用时及精度分析

由表1可知，阈值越大耗时越短，而阈值若设置过大会导致分割不完全。参数阈值下的错误分割数量呈现抛物线趋势，这是由于在阈值很小时很多点云数据被识别成噪声，未分割较多，过分割很少(如图10所示)。而当阈值过大时，分割数少，未分割数也会增加，过分割少(如图11所示)。在阈值取到适中时分割效果最好，此时噪声数量较少，未分割较少，过分割不多，如图12所示。

图10 分割结果(阈值过小时)

图11 分割结果(阈值过大时)

图12 分割结果(阈值适中时)

可以看出，基于区域增长的点云分割算法适用于小曲率变化曲面，尤其适合对连续阶梯平面进行点云分割，如利用SLAM算法生成的建筑走廊等。

2.3 基于RANSAC算法的点云分割

基于RANSAC的点云分割效果由点到平面的距离的阈值和聚类面最小点云数量决定。本试验将距离阈值设为5、7、10、12、15 cm，将迭代条件中剩余点云数量设为100个点和全部点云的20%两种。比较分析分割效果并统计，如图13、图14所示。

图13 基于RANSAC算法的点云分割运行耗时统计

图14 基于RANSAC算法的点云分割错误分割个数统计

剩余点云数量阈值越大，距离阈值越大，运行时间越短。精度方面，在阈值不超过12 cm时，大部分点云可以被识别(如图15所示)，而当阈值达到15 cm和0.2倍点云，会导致大量窗户内部元素未被处理而产生空白，如图16所示。

图15 RANSAC_12 cm_100points

图16 RANSAC_15 cm_0.2*cloud

基于RANSAC的点云分割算法可以较好地提取出建筑物立面点云，但该方法并不能将每块窗户分割开来，也存在一些误分割。

2.4 结合RANSAC和欧氏聚类的点云分割

本文提出一种结合RANSAC和欧氏聚类的点云分割方法，首先用RANSAC对点云进行粗分割，再使用欧氏聚类的方法细分割。本次试验分别将RANSAC算法深度值阈值设为5、7、10、12、15 cm，平面最小点云数量为总数量的0.3、0.35、0.4、0.45、0.5，点到平面欧氏距离阈值为5、7、10、12、15、18、20、25 cm。记录统计运行耗时和错误分割数，默认参数为10 cm、0.4倍点云、10 cm，见表2。

表2 结合RANSAC和欧氏聚类的点云分割在不同参数下的用时及精度分析

参数设置运行耗时/s错误分割数/个RANSAC中深度距离阈值/cm511827130131011501211421510718RANSAC中最小平面点数占总点云的比例0.3120230.3511600.411500.4510710.51071欧氏聚类中欧氏距离阈值/cm5110357109351010916121123151122181150201180251220

由表2可得，阈值变化对运算用时并不明显，整体运行耗时短，与RANSAC算法分割速度接近。从精度来看，该方法可以零错误地分割出立面点云。当利用RANSAC算法进行粗分割时设置深度阈值10～12 cm，最小平面点数大于0.35倍点云，可以较好地提取出墙面及窗沿，再利用欧氏聚类点云分割取较大欧氏距离阈值分割出窗户，得到较好的分割效果，分割结果如图17所示。

图17 结合RANSAC与欧氏聚类的点云分割(深度10 cm，最小平面点0.4倍点云，欧氏距离25 cm)

3 结 语

本文对多种点云分割方法进行研究，对不同方法分割出的点云结果进行精度评定，根据不同的分割结果得出不同分割方法的适用条件。从运算耗时角度来看，欧氏聚类算法最快，区域增长算法耗时最长。从适用性角度分析，欧氏聚类的点云分割算法适用于分割分离的物体，区域增长方法分割点云适合小曲率变化曲面的分割，RANSAC算法适合不同层面的点云数据分层。在此基础上，本文提出了一种结合RANSAC和欧氏聚类的点云分割算法，运算耗时较快，相比几种传统点云分割算法，可以较好地分割出建筑物立面点云。