优化解题路径 提升运算素养*——以解析几何为例谈数学运算素养的培养

□曾 荣

（南通市教育科学研究院，江苏南通 226001）

数学学科核心素养是数学学科课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现.数学运算之所以能列为六大核心素养之一，不仅仅是因为运算是数学学习中的一种必备能力，更是因为数学运算能力本就是数学思维品质的体现，不同层次的数学运算水平彰显了不同层次的数学思维品质.

解析几何的本质是用坐标法研究几何问题，即用代数方法研究图形的几何性质，体现了数形结合的重要数学思想.用代数方法研究的过程中不可避免会涉及较多计算，能否深刻理解运算对象，并结合所研究图形的几何性质，设计合适的运算思路和运算程序，算思结合，这无疑会对提高运算效率、提升学生思维品质起到很好的促进作用.下面结合对2017年江苏高考解析几何运算水平的剖析、运算路径的设计谈对学生数学运算素养的培养.

【2017年江苏高考第17题】试题如下：

如图1，在平面直角坐标系xOy中，已知椭圆(a＞b＞0 )的左、右焦点分别为F1，F2，离心率为，两准线之间的距离为8，点P在椭圆E上，且位于第一象限，过点F1作直线PF1的垂线l1，过点F2作直线PF2的垂线l2.

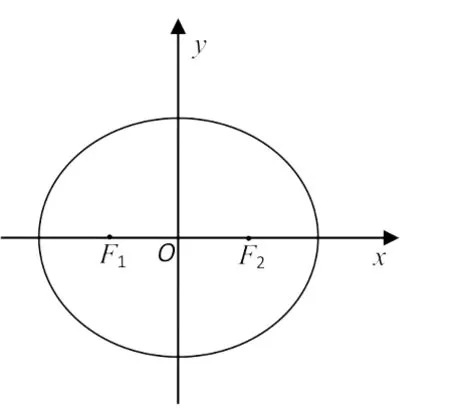
图1

（1）求椭圆E的标准方程；

（2）若直线l1，l2的交点Q在椭圆E上，求点P的坐标.

一、水平剖析

（一）水平一：理解运算对象，设计运算思路，以算助思

【思路分析1】如图2，本题所研究的图形是一个动态图形，对于这样的图形，我们要思考图形因何而动，图形中的动态元素之间存在怎样的联系.动因确定运算对象，牵一发而动全身.本题如果理解为点P运动而引起线段PF1,PF2,QF1,QF2运动，从而导致整个图形在运动，那么我们不妨从设点P(x0,y0)开始.

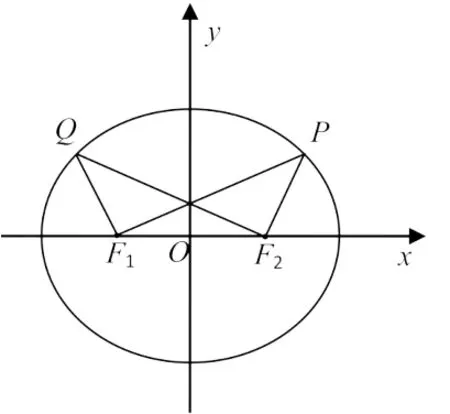
图2

【运算路径1】

（2）由（1）知，F1(-1,0)，F2(1,0)．

设P(x0,y0)，因为P为第一象限的点，所以x0＞ 0，y0＞ 0.

当x0=1时，l1与l2相交于点F1，与题设不符．

当x0≠1时，直线PF1的斜率为直线PF2的斜率为

因为l1⊥PF1，l2⊥PF2，所以直线l1的斜率为，直线l2的斜率为，从而直线l1的方程

直线l2的方程

因为点Q在椭圆上，由对称性，得，即-=1或+=1．

又点P在椭圆E上，故

因此点P的坐标为

【同质思路、路径】考虑到点P为椭圆上的点，我们也可以通过三角换元的方式设出点P的坐标为这种做法，运算的路径和原来基本一致，但变量从两个变为一个，便于学生实际操作．

【思路分析2】如理解点P为PF1与PF2的交点，因为线段PF1,PF2运动导致点P跟着运动，从而导致整个图形在运动，那么我们不妨从设PF1与PF2的方程开始．

【运算路径2】

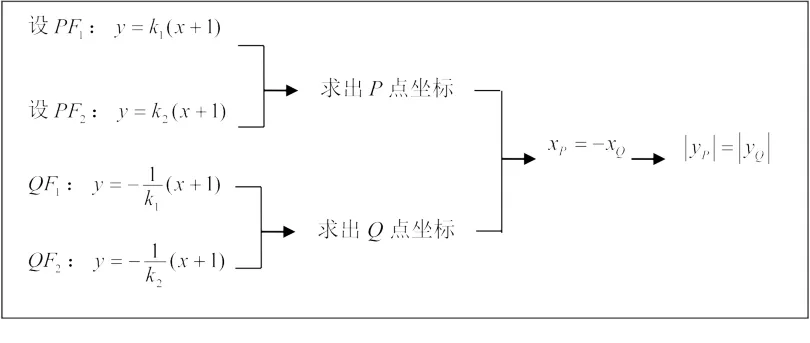
【运算过程2】由⑴知，F1(-1,0)，F2(1,0)．

当PF2斜率不存在，此时l1，l2相交于点F1与题设不符．

当PF1，PF2斜率均存在且不为0．

设直线PF1的方程：y=k1(x+1)，直线

PF2的方程：y=k2(x-1)．

因为l1⊥PF1，l2⊥PF2，F1∈l1，F2∈l2，所以直线l1的方程为直线l2的方程为

又因为P，Q在椭圆E上，由对称性知

所以k1·k2=1．（k1·k2=-1舍去）

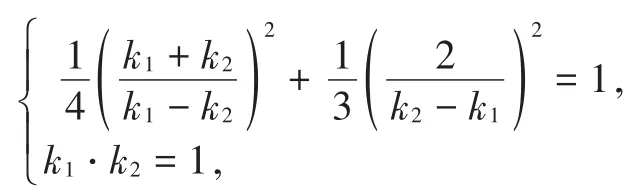
又＞，所以

【解答评析】以上几种方法是解析几何中的常见解法，思维量不大，但运算量较大，需要较扎实的运算基本功、一丝不苟的运算态度和较强的运算自信心方能完成．

（二）水平二：理解运算情境，探求思路切口，算思并举

【思路分析3】解析几何归根到底是研究几何问题，所研究的对象具有怎样的几何背景？这种几何背景又具有怎样的代数特征？能否结合具体的模型寻找解题切口？这道题涉及椭圆的两个焦点，两组焦半径，这是一个典型的焦点三角形模型.考虑焦点三角形与焦半径之间的关系，我们可以从第一定义出发，再结合试题中的垂直关系探求思路切口．

【运算路径3】

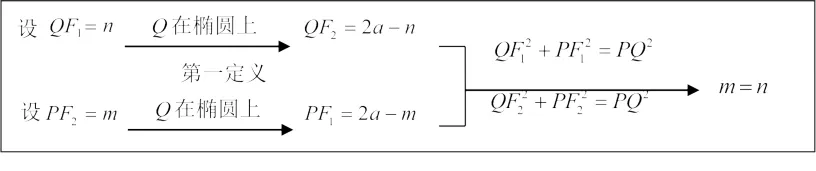
【运算过程3】由⑴知F1(-1,0)，F2(1,0)．

QF1+QF2=2a，PF1+PF2=2a．

设QF1=n，PF2=m，得QF2=2a-n，PF1=2a-m．

当PF2⊥x轴时，x轴与l1交于点F1，不符合题意．

当PF2不垂直x轴时，在△PF1Q中，QF1⊥PF1．

QF21+PF21=PQ2.同理，QF22+PF22=PQ2．

所以n2+(2a-m)2=(2a-n)2+m2．解得m=n．（下略）

【思路分析4】对于焦点三角形模型，我们也可以结合第一、第二定义，将焦半径数量化，再利用试题中的垂直关系，探求思路切口．

【运算路径4】

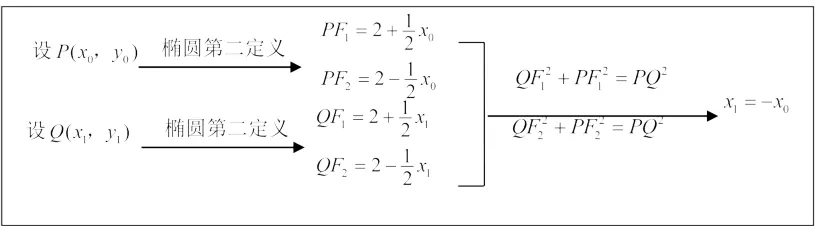
【运算过程 4】设P(x0,y0)(x0＞0,y0＞0)，Q(x1,y1)，

当PF2⊥x轴时，x轴与l1交于点F1，不符合题意．

当PF2不垂直x轴时，因为PF1⊥QF1，PF2⊥QF2，

所以PQ2=QF21+PF21=QF22+PF22．

【解答评析】以上两种运算方法，结合情境中典型的数学模型的常见处理策略，思算并举，便捷地探求出P，Q两点坐标之间的关系，运算量相对较小．

（三）水平三：深挖情境内涵，优化运算路径，以思助算

【思路分析5】解析几何强调用代数方法研究图形的几何性质，我们要善于从不同角度将图形的几何特征代数化.试题条件中的两个垂直条件，在前几种方法中，我们分别转化为斜率之积等于-1、勾股定理进行求解.对于两个垂直关系，我们也可以从向量的角度去理解——数量积为0，先孤立地研究它们背后的代数表示，再综合思考寻求等量关系，探求思路切口．

【运算路径5】

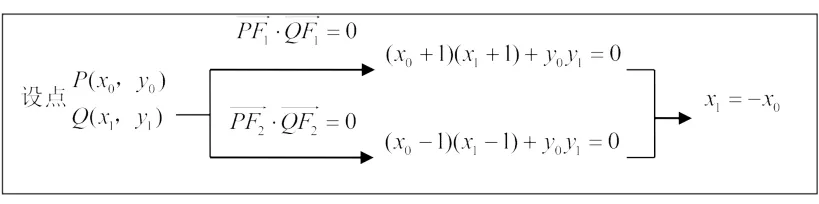
【运算过程 5】设P(x0,y0)(x0＞0,y0＞0)，Q(x1,y1)，

【思路分析6】对于两个垂直，我们还可以用联系的观点认识它们．考虑到两个直角对着同一条线段PQ，故可知P，Q，F1，F2四点共圆，PQ为圆的直径，F1F2为弦．结合圆的几何特征，我们可以知道圆心(xM,yM)在F1F2的中垂线y轴上．

【运算路径6】

【运算过程6】

设P(x0,y0)(x0＞ 0,y0＞ 0)，Q(x1,y1)，

当PF2⊥x轴时，x轴与l1交于点F1，不符合题意．

当PF2不垂直x轴时，因为l1⊥PF1，l2⊥PF2，

所以以PQ为直径的圆M过点F1，F2．

F1F2为圆M的弦，圆心(xM,yM)在F1F2中垂线y轴上，所以xM=0．

【解答评析】很显然，情境内涵的深度挖掘，充分利用图形几何特征，优化运算思路，以思助算，大幅度减少了运算量，提高了运算的效率和准确度．

二、教学启示

（一）理解运算对象，算思结合，重在明理

数学运算素养是在明晰运算对象的基础上，依据运算法则解决数学问题的素养.对于具体的数学运算，我们要结合运算情境，深刻理解运算对象的特征，挖掘其内涵.以思维为基础，运算能力提升才能得到有效的落实.案例中的运算对象PF1,PF2,QF1,QF2，我们可以从动态的角度去研究它们，形成运算思路1，2；我们也可以结合椭圆焦半径的特点去研究它们，形成运算思路3，4；我们还可以结合问题情境中的垂直关系的深度挖掘去研究它们，形成运算思路5，6.对运算对象的不同理解，产生不同水平的数学运算.在这个过程中，数学思维是关键.只有算思结合，重在明理，方能促进数学运算素养的升级发展．

（二）设计运算思路，重在规划，合理优化

在同一数学情境中，不同的运算思路、运算程序的设定，体现了一定的规划设计能力．在具体的运算过程中，学生是稍有想法后便立即动手操作，还是三思而后行，反复寻找更优化的解决路径？在多种方案探寻以后，是凭直觉去感知判断，还是经过理性分析、比较异同之后，再去实践操作？对于案例中的运算，教学中如能结合七种解题线路图帮助学生进行分析，让学生思考每种方法的优劣、每种运算的成本，必然能事半功倍．素养就是在这些设计、比较、操作、优化、反思中形成和发展的．

（三）监控运算过程，主动参与，形成经验

在运算思路、运算程序确定以后，能否准确、快捷地求得运算结果，还需要有良好的运算习惯、全程的运算监控．教师要指导学生自我监控运算过程，主动参与运算方法的选择、运算法则的掌握、运算错误的规避、运算结果的解释的全过程．对于案例中的运算，每种运算的思维关键点、复杂运算出现的关键节点、运算中易出现的错误等我们应实时进行监控，做到心中有数，并在长期的自我监控、主动参与之中形成良好的学习经验．

运算是一种演绎推理，我们应帮助学生学会理性地、有条理地进行运算和思考．我们应从运算的背景、内容、过程、方法及其蕴含的数学思想等出发，全方位地思考提升学生的数学运算水平，通过运算促进学生数学思维的发展.