汽轮机变工况下调节级压力预测模型及应用

2019-05-09罗云陈雪林李瑞东苏永健徐义巍晁俊凯李鹏竹任海彬

发电技术 2019年2期

罗云，陈雪林，李瑞东，苏永健，徐义巍，晁俊凯，李鹏竹，任海彬

汽轮机变工况下调节级压力预测模型及应用

罗云1,2，陈雪林1，李瑞东3，苏永健1，徐义巍1，晁俊凯1，李鹏竹1，任海彬1

（1．宁夏京能宁东发电有限责任公司，宁夏回族自治区银川市 750001； 2．北京东方国信科技股份有限公司，北京市朝阳区 100012； 3．北京京能电力股份有限公司，北京市朝阳区 100025）

为监视汽轮机通流部分的健康状况和进行故障早期诊断，以汽轮机变工况计算为理论基础，基于弗留格尔公式和Weierstrass逼近定理，建立了调节级压力的多元回归模型。根据某660MW间接空冷机组大修后的运行数据对模型进行回归分析和验证，结果表明：模型具有很高的拟合度，自变量对因变量影响显著；稳态工况时，预测结果与实测值趋势一致，相对误差约为1.2%，实现了变工况下调节级压力软测量。将模型应用于电厂分布式控制系统中，建立了汽轮机通流部分故障的预警系统。

汽轮机；故障诊断；调节级压力；预测模型；多元回归分析；分布式控制系统(DCS)

0 引言

随着电力体制改革不断深入，超临界600MW以上等级的机组已成为火力发电厂的主力机型，但超临界机组在运行过程中也存在一些问题。一方面，超临界机组在运行中不能通过有效的措施降低炉水中的杂质，导致蒸汽盐分含量高。含盐蒸汽通过汽轮机做功后，压力降低，溶解在蒸汽中的盐类析出，会引起汽轮机通流部分结垢[1-2]。另一方面，在机组启动过程中，普遍存在炉管氧化皮生成和脱落现象，而氧化皮颗粒随蒸汽进入汽轮机后，会改变喷嘴和动叶的线型，降低其空气动力性能；增加叶片表面的粗糙度，增大叶片的摩擦损失；增大汽封间隙，使级间漏汽量增大[3]，从而造成机组运行中效率降低，热耗增加，调节级压力不断升高。因此，建立调节级压力预测模型，进行汽轮机通流部分健康状态评估和故障早期诊断，对于保证机组安全、经济运行具有重要意义。

目前，关于对火电厂运行参数预测建模的文献很多。依据BP神经网络可以实现任意复杂非线性关系映射[4]的特点，大多都采用神经网络算法，如文献[5]建立了凝汽器真空的神经网络预测模型；文献[6]建立了超临界机组过热器壁温的神经网络预测模型；文献[7]建立了神经网络算法的锅炉NO排放量预测模型。虽然这些模型通过样本检测，预测效果很好，但神经网络模型的拓扑结构很难写入电厂的DCS系统中，因此，一般只用于离线预测，模型适用性不强。笔者尝试通过理论计算得到汽轮机各工况下的调节级压力，但计算过程也存在以下3个方面的问题：1）计算过程需要较多的原始数据，由于测点的测量精度影响不可避免的会产生观测误差。2）计算过程要求通过喷嘴和动叶的蒸汽流量相等，但实际热力过程中，通过喷嘴后的蒸汽分成3部分：第1部分(大部分)通过动叶进入下一级；第2部分通过喷嘴组与转子之间的汽封(过桥汽封)漏入中压缸；第3部分由动叶顶部的汽封直接进入下一级。3）全开阀门和部分开启阀门喷嘴组的通流面积不能直接测量，只能查阅设计资料获得。由于喷嘴组制造和安装的误差，设计通流面积与实际通流面积会有一定的偏差。因此，通过理论计算得到的调节级压力并不是绝对准确，只是近似准确，而且计算过程复杂。

鉴于神经网络模型应用的局限性和机理模型的复杂性，本文以汽轮机变工况计算为理论基础，分析了机组运行中调节级压力的影响因素，基于弗留格尔公式[8-9]和Weierstrass逼近定理[10]，分别建立了调节级压力对每个影响因素的数学模型，在此基础上建立了调节级压力的多元回归模型。以某660MW机组大修后的运行数据对模型进行回归分析和参数求解，得到了回归方程，实现了该机组调节级压力预测。

1 调节级压力理论计算

由于调节级的通流面积在汽轮机变工况运行中随调节阀开启的个数而改变，级组压比也随着通流面积变化而变化，因此调节级变工况计算时需要同时考虑通过全开调节阀的汽流和通过部分开启阀的汽流。通过调节级变工况计算调节级后压力时，需要借助调节级特性曲线。调节级特性曲线可直接查阅厂家资料或者通过调节级特性曲线快速计算法得到[7,11-12]，调节级后压力具体计算步骤如下：

1）已知主蒸汽压力0和温度0，全开调节阀后和部分开启调节阀后的压力0ʹ和0ʺ，调节级后蒸汽温度1(已知量直接测量得到)。

2）假设调节级后压力为1，根据调节级后温度1，调用水蒸气特性计算程序，计算调节级后蒸汽比焓1。

3）调用=()特性曲线方程，由压比ʹ=1/¢0，查出对应的ʹ，利用式(1)、(2)计算全开调节阀的蒸汽流量¢：

式中：ʹ为全开调节阀的蒸汽流量，kg/s；0、ʹ0、1分别为主蒸汽压力，全开调节阀后压力和调节级后压力，MPa；0为主蒸汽比容，m3/kg；ʹ为喷嘴流量比；ʹ为全开调节阀喷嘴组面积，cm2；ʹ为系数；cr为喷嘴组的临界压比，过热蒸汽为0.546。

4）调用=()特性曲线方程，由压力比ʹ=1/ʹ0，查出对应的²，利用式(1)计算部分开启蒸汽调节阀流量²。

5）利用式(3)、(4)计算Dʹ和D²：

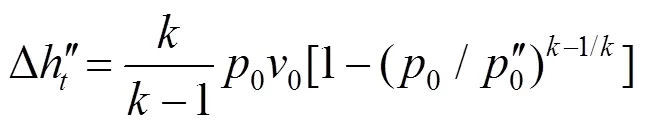
式中：为等熵指数，=1.3；Dʹ为通过全开调节阀蒸汽的理想比焓降，kJ/kg；D²为通过部分开启调节阀蒸汽的理想比焓降，kJ/kg。

6）利用式(5)、(6)计算全开调节阀和部分开启调节阀2部分蒸汽的速度比ʹ和²：

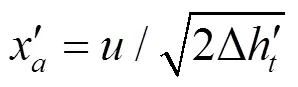
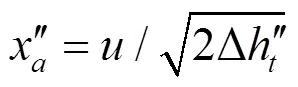
式中为轮周速度，m/s。

7）调用调节级=(x)特性曲线，根据式(7)、 (8)分别计算通过全开调节阀和部分开启调节阀2部分蒸汽在动叶出口的实际比焓ʹ1和²1：

式中：0为主蒸汽比焓，kJ/kg ；ʹ和²分别为全开调节阀和部分开启调节阀调节级轮周效率。

8）根据式(9)计算2部分蒸汽在调节级室内混合后的实际比焓值21：

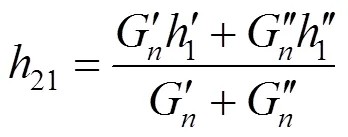
9）当1=21，认为调节后压力1假设成立，否则重复步骤1）—7），每次对1增加0.001进行迭代计算，直到得到正确的1。

综上所述，调节级压力计算流程如图1所示。

图1 调节级压力计算流程图

2 调节级压力数据建模

2.1 调节级压力的特征变量选取

由调节级压力的机理计算模型可知，调节级压力由主蒸汽压力、温度、调节阀开度、调节级特性(特性曲线和调节级几何尺寸)决定。对特定的机组，调节级特性是固定的；机组运行中，主蒸汽温度基本保持不变；主蒸汽压力随着负荷变化线性变化；调节阀开度受机组负荷和背压影响；为避免自变量之间具有完全多重共线性关系，只选取负荷和背压作为调节级压力建模的自变量。

2.2 多元回归分析

多元回归分析(multiple regression analysis，MRA)是指在相关变量中将一个变量视为因变量，其他一个或多个变量视为自变量，建立多个变量之间线性或非线性数学模型数量关系式，并利用样本数据进行分析的统计分析方法。另外也有讨论多个自变量与多个因变量线性依赖关系的多元回归分析，称为多元多重回归分析模型[13]。多元线性回归模型可表示为

式中：为因变量；1,…,x为自变量；0为回归常数；1,…,为偏回归系数；为随机误差。对1,…,x进行变量转换，式(10)可以转化为多种形式的多元非线性回归模型，如指数模型、对数模型、多项式回归模型等。

2.3 确定调节级压力多元回归模型形式

2.3.1 调节级压力与机组负荷的一元回归模型

汽轮机变工况过程中，部分开启的阀们未全开前，1/²0大于1/ʹ0，由公式(3)、(4)可知，通过全开阀门蒸汽理想比焓降Dʹ大于通过部分开启阀门蒸汽的理想比焓降D²。而2部分蒸汽在调节级室混合后的实际比焓值21一样，所以，通过全开阀门蒸汽的有效比焓降大于通过部分开启阀门蒸汽的有效比焓降。也就是说，在第1个调节阀全开后，随着其他调节阀开启，蒸汽流量增加的过程中，调节级的有效比焓降会减少。

而对于末级，如果背压不变，随着蒸汽流量增加，末级前后压比减少，蒸汽有效比焓降增加。调节级和末级有效比焓降反向变化，增量相互抵消，加之中间各级组的压比不变，各级的理想比焓降、效率、有效比焓降基本不变[8]，使得整机的有效比焓降基本保持不变。

综合以上分析，由汽轮机功率方程式可知，背压不变时，汽轮机功率与蒸汽流量成线性变化。

对于凝汽式汽轮机，将调节级后的所有压力级取成一个级组，忽略调节级温度变化，应用弗留格尔公式[12]，则有

式中：、分别为变工况的主蒸汽流量、调节级后压力；0、0分别为设计工况的主蒸汽流量、调节级后压力。

对特定的机组，0/0为常数，根据式(11)可推导出

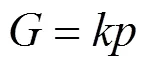
式中为常数。

建立调节级压力与机组负荷的一元回归模型为

式中：为调节级压力，MPa；1为机组负荷，MW；ʹ0为回归常数；ʹ1为偏回归系数；为随机误差。

2.3.2 调节级压力与背压的一元回归模型

机组运行过程中，由于凝汽器循环水进水流量或温度变化导致背压升高时，低压缸末级焓降减少，为维持负荷不变，汽轮机开大调节阀增加蒸汽流量，蒸汽流量的增加，又会造成背压升高，达到稳态是一个非常复杂的热力过程。因此，通过理论分析，建立调节级压力与背压的函数关系是很困难的。由Weierstrass逼近定理可知：任何函数在一定范围内都可用多项式以任意精度逼近。因此，机组负荷不变时，调节级压力可由背压的多项式表示：

式中：2为背压，kPa；0为回归常数；1,…,为偏回归系数。

2.3.3 调节级压力多元回归模型

根据式(13)、(14)，建立调节级压力的多元回归模型为

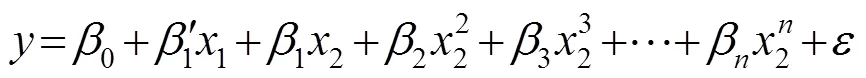
式中：ʹ1,1,…,为偏回归系数；为多项式次数。

3 案例分析

3.1 案例电厂数据样本

以某超临界660MW机组为研究对象，为使建模数据样本包含各种工况，每间隔1min采集一次数据，采集了该机组连续运行15天的负荷、调节级压力、背压数据，共计20165组，其中负荷变化范围325~624MW，背压变化范围为11.2~39.8kPa。采用时窗公式法[13]，筛选了4900组准稳态过程数据，数据样本如图2所示。

图2 数据样本

3.2 回归分析

3.2.1 模型拟合优度检验

拟合优度用于检测回归模型对样本数据的拟合程度。选择不同的值，用数据样本对模型(15)进行回归分析，判定系数2如表1所示。由表1可知，当大于2时，2增加量减少；当大于3时，2不再增加，为避免模型出现“过拟合”的问题和模型过于复杂，选择=2。

表1 不同n值与判定系数R2

=2时，模型的拟合优度指标如表2所示，复相关系数=0.9988，接近于1，说明调节级压力与自变量1、2、22高度正相关。判定系数2=0.9977，说明机组负荷和背压可解释调节级压力变化的99.77%，0.23%由其他因素决定。标准误差为0.1014，数值较小，模型精度较高。

表2 n=2模型拟合度指标

3.2.2 模型整体显著性检验

回归模型的整体显著性检验，就是检验全部自变量对因变量的共同影响是否显著。由表3模型方差分析表可看到，Significance(为显著性统计量)的值为0，小于显著性水平0.05 ，说明该回归方程回归效果显著，且方程中至少有一个回归系数显著不为0。

表3 模型方差分析

3.2.3 回归系数显著性分析

模型整体显著并不表示每个自变量对于因变量的影响都是显著的[14-15]，故进行回归系数显著性分析，检验当其他自变量不变时，该回归系数对应的自变量是否对因变量有显著影响。由表4模型的偏回归系数可看出，自变量统计量的显著性值均小于0.05，通过检测。

表4 回归系数分析

3.2.4 回归方程估算

3.3 模型验证

以该机组某日6:00—16:00的实际运行参数为检测样本，每间隔1min采样一次，对模型进行检测，模型预测曲线与实时曲线比较如图3所示，误差如图4所示。由图3和图4可知，在稳定工况时，调节级压力预测值与实时值误差绝对值小于0.2MPa，相对误差约为1.6%，具有较高的精度。变工况时，由于机组背压滞后负荷变化，预测值误差稍大，但对整体预测效果没有影响。

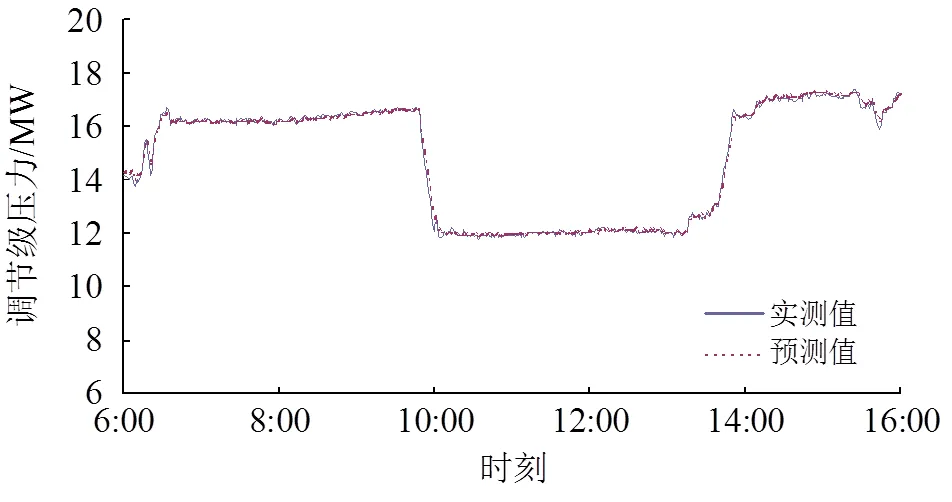
图3 实测曲线与预测值曲线图

Fig. 3 Measured curve vs. predicted value graph

图4 预测值误差散点图

4 模型应用

4.1 变工况下调节级压力异常预警

DCS系统参数预警的传统方法采用固定的最大值和最小值设置，而对于随机组工况变化的参数，显然不能达到监视其是否偏离正常值的目的。如调节级压力预警只根据设计阀门全开(VWO)工况的压力值设置了超压预警，即便是通流部分出现故障，调节级压力也很难超过VWO工况的压力，因此，这样的预警设置没有实质性意义。

根据机组当前负荷和背压，由调节级压力回归模型计算得到预测值，与实时监测值对比，建立变工况下调节级压力异常预警系统，逻辑设计如图5所示。

4.2 通流部分级组故障诊断

汽轮机通流部分故障最终会导致通流面积增加或减少[16]，通流部分结垢时，级组通流面积减少，级组压比减少[17]；通流部分磨损时，级组通流面积增加，级组压比增大。以该660MW机组为对象，将一段抽汽到二段抽汽中间各级取作一个级组，机组运行中该级组压比的变化范围为0.665~0.705，为排除高压加热器故障造成调节级压力和级组压比变化，以高压加热器上、下端差值作为判断回热系统运行正常的边界条件，建立通流级组故障预警系统。

图5 调节级压力异常和级组故障预警逻辑设计图

5 结论

汽轮机调节级压力一定程度上反应了通流部分的健康状态，是汽轮机运行过程中的重要监视参数。本文介绍了调节级压力的理论计算方法，鉴于其计算的复杂性和存在较大的误差，在数据驱动下，结合机理分析和多元回归分析建立了调节级压力的回归预测模型，并将模型应用于电厂DCS系统中，建立了变工况下的调节级压力异常和级组故障在线预警系统，该研究成果的特点和意义在于：

1）采用调节级压力和级组压比同时变化的方法对汽轮机通流部分故障进行在线诊断，相对于模糊神经网络故障诊断法和特征(或者当量)通流面积诊断法，具有快速诊断和故障精准定位的优势；

2）优化了DCS系统的预警功能，实现了DCS系统智能预警，为重要参数变工况下的预警设置提供了一种新方法。

[1] 丁旭春，王毅，殷志龙，等．超临界630MW机组汽轮机通流结垢诊断及处理[J]．热力发电，2013，42(11)：138-140．

[2] 杨涛，胥建群，周克毅，等．汽轮机通流部分结垢与热力参数变化的关系分析[J]．江苏电机工程，2013，32(2)：71-74．

[3] 刘志江，李续军，刘向民．超临界压力汽轮机固体颗粒侵蚀的表面硬化处理技术[J]．中国电力，1996，37(2)：25-28．

[4] 朱永利，尹金良．人工智能在电力系统中的应用研究与实践综述[J]．发电技术，2018，39(2)：106-111．

[5] 王建国，孟娜，殷鑫．基于粒子群优化算法的凝汽器真空预测模型[J]．动力工程学报，2012，32(10)：815-820．

[6] 邓博，徐鸿，郭鹏，等．变负荷下超临界机组过热器壁温预测[J]．中国电力，2018，51(3)：13-20．

[7] 孙宝民，信晶，杨斌，等．基于独立主成分预测电站锅炉NO[J]．中国电力，2018，51(3)：39-43．

[8] 李维特，黄保海．汽轮机变工况热力计算[M]．北京：中国电力出版社，2001：143-145．

[9] 靳智平．电厂汽轮机原理及系统[M]．北京：中国电力出版社，2004：88-92．

[10] 将尔雄，赵风光．数值逼近[M]．上海：复旦大学出版社，1996：183-185．

[11] 李慧君，赵翔．汽轮机调节级特性曲线快速算法改进[J]．热力发电，2016，45(10)：94-98．

[12] 张利平，王夕阳，王睿，等．基于MATLAB的汽轮机调节级变工况计算[J]．华北水利水电大学学报，2015，36(3)：72-72．

[13] 颜节礼，唐建荣．应用统计学[M]．西安：西安电子科技大学出版社，2016：103-104．

[14] Jiang X，Liu P，Li Z．Data reconciliation and gross error detection for operational data in power plants [J]．Energy，2014(75)：14-23．

[15] 杨勇平，袁星，黄圣伟，等．火电机组湿法脱硫系统能耗的回归分析[J]．工程热物理学报，2012，33(11)：54-56．

[16] 杨勇平，杨昆．汽轮机通流部分故障的热力判据[J]．热能动力工程，1999，14(5)：347-349．

[17] 李勇，徐君诏，黄萍力．凝汽式汽轮机通流部分结垢诊断方法研究[J]．汽轮机技术，2008，50(5)：286-287．

Prediction Model and Application of Turbine Regulating Stage Pressure Under Variable Conditions

LUO Yun1,2, CHEN Xuelin1, LI Ruidong2, SU Yongjian1, XU Yiwei1, CHAO Junkai1, LI Pengzhu1, REN Haibin1

(1. Ningxia Ningdong Power Generation Co., Ltd., Yinchuan 750001, Ningxia Hui Autonomous Region, China; 2. Beijing Jing Business-intelligence of Oriental Nations Corporation Ltd.,Chaoyang District, Beijing 100012, China; 3. Beijing Jingneng Power Co., Ltd., Chaoyang District, Beijing 100025, China)

Using the calculation of the variable conditions for steam turbines as the theoretical basis, a multivariate regression model for regulating pressure was established based on the Frugell formula and the Weierstrass approximation theorem. According to the historical operation data of a 660MW generating set, the model was subjected to regression analysis and verification. The results show that the model has a high degree of fit, and the independent variable has a significant influence on the dependent variable; When the steady state conditions are met, the predicted results are consistent with the measured values and the relative error is about 1.2%, which enable soft pressure measurement of the regulation stage. The model was applied to the distributed control system (DCS) of the power plant, and an on-line warning system was established to adjust the pressure anomaly and the partial flow malfunction in the turbine under variable conditions.

steam turbine;fault diagnosis; regulation stage pressure; predicted model; multiple regression analysis; distributed control system(DCS)

10.12096/j.2096-4528.pgt.18173

2018-12-11。

罗云(1981)，男，高级工程师，从事火力发电厂运行管理和大数据应用研究工作，ayunmeng@163.com；