浅谈如何使数学教学内容恰当融入学生的日常生活

2019-05-09李玉兰

海外文摘·艺术 2019年4期

李玉兰

（湖南省商业技师学院，湖南株洲 412000）

众所周知，中职学生缺乏学习的积极性，更谈不上学习知识的自觉性，有两个原因：一是因为基础不好，认为老师所讲内容“比较难”接受不了而拒学；另一方面，认为一般生活中“用不上”，从而导致学习没有热情。所以，要尽可能地使用学生自己身边的事与数学内容联系起来，使教学的内容通过教学策划、提炼加工后应用到生活中去，解决身边的生活现实问题，才能让学生体会到学习数学的重要性。我采取了如下做法：

1 结合学生专业实际需要，让教学内容走进日常生活

职业教育属于应用性教育，学习的目的是为生产生活服务的，总的指导思想是以服务为宗旨、以就业为导向。学生在专业知识和技能掌握时需要必备的数学知识是数学课的主要教学任务，所以数学教学又必须服务于专业需要，同样的课程内容，对于不同专业的学生的侧重点是不同的。如三角函数，对计算机专业的学生仅需要理解、掌握基本概念和计算方法就行；而电子专业的学生，关键是要理解振幅、周期、频率、初相、相位等概念，因为这些是今后专业学习单相、三相交流电的基础，用五点法作图画正弦曲线也是必须掌握的；但对于数控专业的学生，重点是对三角函数计算的要求很高，因为数控编程中需要大量使用三角函数进行坐标计算；对会计专业的学生，没有必要学习这个方面的内容，可根据学期课时情况进行选择，所以要根据学生的专业需要，选准知识的侧重加以区分讲解、选择相应适用的案例教学。

数学备课时，选择适合职业学生特点的组织形式，争取85%的精力要放在如何抓住学生的注意力上，是否能把学生的注意力吸引到课程内容上，并且保持这种注意力，是一节课的成功与否的关键。利用学生自己身边的事情将教学内容导入日常生活中，这样能最大限度地吸引学生的注意力，感觉数学就在身边。

如在学习完平面性质“不在同一直线上的三点，可以确定一个平面”后，我告诉学生，如果你家中的地板不很平，你应该买一个三条腿的桌子，因为不在同一直线上的三条腿，可以确定一个平面，从而使这个桌子不会摇动，桌子上杯中的水也不会溢出来，而四条腿的桌子就不一定很平稳。这也正是高速公路的测量员为何将他们的经纬仪放于三角架上，或者摄影师在三角架上固定他们的照相机的原因。

公园里，当木匠建造一个小木屋时或亭子时，他们常常经过垂直木架的对角线上用钉子钉一块木板，他们这样做的目的是防止正方形变为平行四边形，引起房屋倒塌。正是这些相交或不平行的线，才使几何建筑更加坚固。还有在植树时，为了让树长直，常在树的周围用木桩或竹桩固定，这些桩、树、和地面构成三角开。

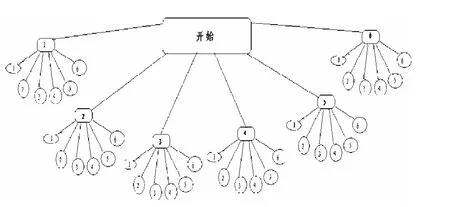
图1 抛掷2个骰子树形图

图2 即位图

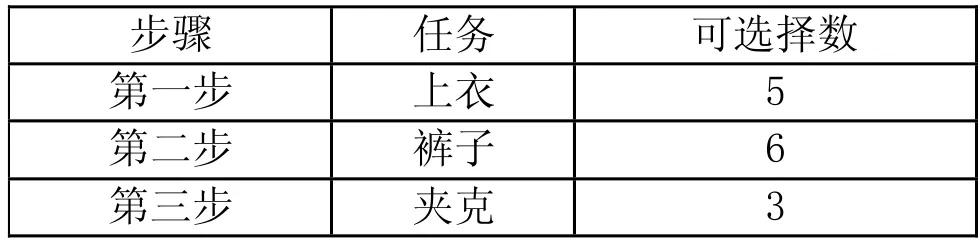
表1 步骤任务

又如在学习直线与直线的位置关系之后，我告诉学生，我们熟悉的车内导航系统，司机能够搜索到距离自己位置最近的肯德基餐厅。为了获得汽车的具体位置，这个系统确认汽车位于不平行的直线（即路）上，因为这些直线必交于一点，于是这个导航系统就能确定这辆车的确切位置，引导司机找到最近的餐厅。

只有使所学知识与现实生活联系起来，才能让学生感受到知识的真实有效性，激发学习动力，才能顺利完成教学任务，达到教学教育的目的。

2 创设实际生活情境，让教学内容在实际操作中融入现实生活

学生的注意力难于集中，要想方设法创设教学内容与学生生活环境、知识背景密切相关的案例，或者创设能让学生观察、操作的学习情境，使学生能通过交流、反思、猜想等一系列活动去体验生活中数学知识的产生与作用，获得积极的感受数学的神奇力量。

如在学习完集合一章之后，我让学生进超市观察集合在商场中的运用，寻找商场中的集合与集合中所含有的元素。学生开始时感到茫然，我把他们带到放牛奶的地方，告诉他们这里的牛奶就是一个集合，其中的元素有蒙牛牛奶、光明牛奶、南山牛奶、卡士牛奶……等等，学生一下子明白了，然后寻找更多的集合和集合中的元素。要求以组为单位进行记录并进行评比，看看哪组找的多？哪组元素更全面？学生们找到了很多集合，如有方便面集合、食用油集合、水果集合、洗衣粉集合、玩具集合……并将里面的元素一一列举出来了。之后我提问学生，如果没有集合，你想像一下会有哪些不利？经过刚才的观察，学生明白了如果没有集合，顾客很难找到自己需要的东西。最后我让学生自己设计一个店，要求有店名、销售商品类别，设计商品的种类，如何规划布局商品，为什么这样布局？重点是如何摆放这些物品、如何进行总体设计。以组为单位，课后进行讨论，并把方案写成文稿，下一次上课时，每组派一同学上台讲述自己的设计方案与意图，说说你的商店的特点和构思的新颖性在哪些方面？你的促销策略有哪些？对员工的激励机制是什么？然后进行评比。经过完成这一系列的任务，学生的思维打开了，开店设计各有特色，有开零食店的、有开水果店的、有开服装店的、有开面包店的……而且布局很有想像力和创意思维，经营的产品有特色，店面的空间设计也很人性化，真正做到全心全意服务于顾客、各方面都考虑的是方便顾客、以顾客为中心，以盈利为重点。

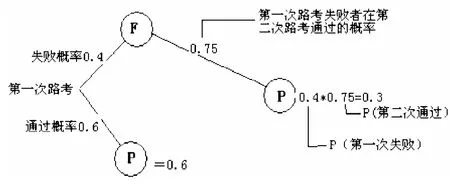
图3 两次通过路考的概率树图

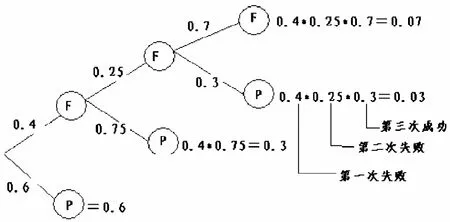
图4 “未通过—未通过—通过”的分支图

实践操作、探讨交流也是学生学习数学的重要方式。讨论问题中鼓励学生发表自己的意见，并与同伴进行交流思考解决问题的最佳方案，必要时老师提供适当的帮助和指导，让数学知识和数学课堂融入实际生活中，充分发挥学习的主动性。

又如在学习第九章立体几何时，为让学生掌握平面中如何画出立体图形，先让学生观察一些立体图形，让学生说出图形中有几个面？几条直线？图中还有一些什么？它们的位置关系是怎样的？等等，然后让学生观察图中的平面是什么形状？引导学生得出：是平行四边形，然后让学生对照实物去感知实物图形与平面中的产体图形的画法。然后继续让学生看粉笔盒，看有多少个面？要求学生课前用纸板作一个这样的盒子，上课时提问学生至少要多少纸板？这样学生切实地感悟到表面积含义的内涵，同时开始进行测量长、宽、高，并进行计算。有了上述的经历，再让学生思考圆柱、圆锥的表面积包括哪些部分？各部分如何测量？学生在测量圆柱侧面积是遇到了困难，提示学生将侧面沿一条线剪开后展开，学生立马明白了。所以数学教学不是简单地告诉学生结论如何，最好是从学生身边的、熟悉的、具体的事物中化抽象为具体，让学生想明白是怎么一回事，学生才能掌握数学和理解数学，达到真正运用数学，。

在学生掌握了这些数学知识和学会了测量方法以后，我让学生进行了两课时的实地测量，让学生完成了如下任务。（1）以小组为单位，完成以下测量任务：1）每组测量一栋教学楼的楼高；2）测量每栋楼内的垃圾桶的体积；3）测量田径场的面积；4）测试学校的旗杆、蓝球架等是否垂直于地面等。（2）记录测量的全过程，你们是如何进行测量的，在测量过程中遇到了哪些困难，是如何解决的？（3）通过测量，估算一下我校一天的垃圾量，来预测一下我们的环卫工作者的工作辛苦程度等。

通过亲身体验，让数学走进生活，让学生在生活中看到数学，接触数学，激发学生学习数学的兴趣，很好地体验和理解数学，也增强了学生学习的自主性和思维的创造性。

3 对教材内容进行再加工、拓展，让教学内容骤步融入学生初步的应用意识和解决问题的能力中

根据学生的具体情况，有创造地进行教学设计，培养学生应用数学的意识和解决问题的能力，这是数学教学的重中之重。

如在讲§10.1计数原理时，分类计算原理学生容易理解并掌握，但分步计数原理看似简单，实际运用就没那么容易了。

分步计数原理的内容是：一般地，如果完成一件事，需要分成n个步骤，完成第1个步骤有

种方法，完成第2个步骤有

种方法，……，完成第n个步骤有

种方法，并且只有这n个步骤都完成后，这件事才能完成，那么完成这件事的方法共有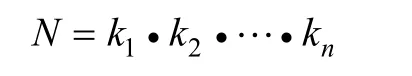

为使这个使数学理论形象化，我先介绍课本外的一个内容‘树形图’，来辅助学生理解直观计数。

例如，若抛掷2个骰子，朝上的数字能有多少种不同的数对？此问题中要强调的是骰子是不同的，假设是一红一绿，红2绿3和红3绿2是不同的情况，我们可以有有序数组（红数，绿数）来表示骰子的数对，如（4，5）表示红4绿5，则可以用图1的‘抛掷2个骰子树形图’直观图来描述这个问题。

第1个分支可组成6对数组（1，1）（1，2）（1，3）（1，4）（1，5）（1，6），同理第2个分支也可得到6对数组（2，1）（1，2）（2，3）（2，4）（2，5）（2，6），继续得到共36对数组。

（1，1）（1，2）（1，3）（1，4）（1，5）（1，6）

（2，1）（2，2）（2，3）（2，4）（2，5）（2，6）

（3，1）（3，2）（3，3）（3，4）（3，5）（3，6）

（4，1）（4，2）（4，3）（4，4）（4，5）（4，6）

（5，1）（5，2）（5，3）（5，4）（5，5）（5，6）

（6，1）（6，2）（6，3）（6，4）（6，5）（6，6）

并提醒学生注意：在某些计数问题中元素是可重复的，如打开号码锁可以用相同的数字去拨，如23－23－23是有效的组合，而在某些计数问题中的元素是不可重复的，如动物派对，同一种动物不能使用2次或更多次，让学生学会不同情况不同分析。

在学生初步掌握树形图之后，提示学生解答计数问题的一个有用的技巧是如图2所示，画一系列空格来表示完成每一步任务的方法数，即位图。

一个成功人士通常把一个复杂的情况分解成简单的几个部分来解决。这就是我们数学上通常用到的分步计数原理，在计数问题中认为事件不是一次就发生的而是按不同的阶段发生的，第一件事发生，然后就是第二、第三、……，若我们能数出每个阶段的情况，就能结合此信息推导出最后的结果。

我选择了这样一个实例：选择套装计数来让学生进一步掌握知识点，并解决实际问题。

Ramona为春季流行时尚设计了新的款式。她设计了5种上衣、6条裤子和3种夹克。若我们以一件上衣、一条裤子和一件夹克为一套，Ramona的模特可以穿出多少种没有重复的套装？

设想一棵树，最上端分支代表选择上衣，有5个分支；中间分支代表选择裤子，上衣的5个分支又分别生出6个分支的裤子，至此共有30个分支；最下端分支代表选择的夹克，上述每个分支又各加3个分支代表夹克，从而得到90个不同的分支。因此，Ramona的模特有90套不同的套装可穿。

上述问题用计数原理来解答可以如下来考虑

通过任务来考虑套装数，列出‘步骤任务表1’来进行分析。

通过计数原理，Ramona的模特有 5×6×3=90种套装。

在学生掌握上面的计算方法之上，我告诉学生：尽管数学的发展开始只有自身的价值，但通常最后有重要的作用，像计数这件事，在解决复杂问题，如数以百万计的电话通过网络的路由问题，或者数百架飞机航线的优先安排问题中发挥了重大的作用。

之后，我提出这样一个问题：你相成为百万富翁吗？

我先告诉学生关于彩票历史：

彩票在古代就出现了，如古罗马帝王尼绿把奴隶或是别墅作为礼物送给出席他的盛宴的客人，奥古斯都凯撒利用公益彩票来募集资金修建罗马。最早的公益彩票出现于16世纪的意大利的佛罗伦萨，1870年意大利统一后，这种彩票又演变成为意大利的国家彩票，在这种彩票上有1～90之间的5个数字，中彩的人必须猜中5个数字方可获得彩票价格的1000000倍收益，90个数中选出5个的可能结果，C（90，5）＝43949268，因此同许多其他彩票一样，对于发行方而言是绝对有利的，而对买彩票方而言是很不利的。

然后告诉学生有这样一个真实的报道：

据调查，超过四分之一的美国人认为退休后通过买彩票有更多的机会挣钱，而不是按部就班地对他们拥有的钱进行投资。1999年7月，美国消费者联合会进行了一项调查，发现许多美国人并不理解他们中彩票的机会有多少。他们没有意识到通过定期节约投资可以积攒数十成或数百万美元。调查还发现年轻人和低收入人群可能最不理解通过多年的定期存储可以积累资产。例如，若一人以7%的利润连续每周投入25美元，投资40年，投资获得的终值几乎是3000000（3百万）美元，但在调查中不足三分之一的人认为这项投资的终值会多于150000（15万）美元。收入在3500美元左右的人群中40%的认为彩票要比储蓄来说更容易致富。

最后布置这样一个任务：请以小组为单位，理解这个计数原理并结合资本增长（复利公式）的知识，正确认识共同基金而不是彩票才是安全的财产致富之路。请用计算数据说明问题

通过这一过程的学习，让所学的知识融入现实生活中，使学生对实际问题有正确的认识。

在概率学习的过程中，我也用树形图帮助学生理解，使概率计算公式形象化。案例如下：

美国有些洲的驾照教科文是这样的：首先是笔试，通过笔试后方可参加路考（限定次数）。在限定的次数内还没有通过的话就要重新参加笔试。下面计算减少路考的限制次数对投考者的影响。

这是一个条件概率的问题。通常参加路考的机会只有3次，有些人认为应该只给2次机会，而有些人则感到对于那些第三次才通过的人而言，这样的规定实在过于苛刻。

从历史纪录来看，60%的人第一次路考就能通过，在第二次中有75%的人通过，而在第三次路考中只有30%的人通过。

（1）第一次未通过，第二次才通过的概率是多少？

（2）前两次都没有通过，第三次才通过的概率是多少？

分析：

（1）第一次未通过，第二次通过的概率P（先失败后通过）＝P（失败）P（通过|失败）＝0.40.75＝0.30

具体理解的直观概率树如图3。

这就意味着投考者经过两次尝试才能通过路考的概率为0.3。