地下结构的抗震设计及土层处理方法的探讨

丛珩易

摘 要：本文应用反应位移法，对一地铁车站进行了抗震设计中的受力分析，同时采用比较分析的方法，讨论了地层地质结构两种处理方法，即近似为分层土或匀质单层土处理，讨论了两种处理方法在地层位移、地震土压力、地震剪应力、结构地震惯性力计算上的偏差，最终得出分层土较匀质单层土更符合实际情况的结论，从而能够为实际设计中提供参考。

关键词：地下结构;抗震设计;反应位移法;土层处理

中图分类号：TU93 文献标识码：A 文章编号：1671-2064（2019）06-0149-02

0 引言

城市地铁方便、快捷、运行流量大等特点，已成为我国主要的公共交通运输方式，其在城市运输中的作用也愈发不可替代。然而，我国是一个地震灾害多发的国家。因此，对地下结构抗震的研究具有很大的重要性。目前对地下结构抗震的研究方法有自由场变形法、反应位移法、有限元反应加速法、时程分析法等等。由于反应位移法能够更好的体现土与结构之间的相互作用、且计算成本较小，成为在地下结构抗震设计过程中应用较广的方法之一[1]。在应用反应位移法的地城地质结构处理过程中，可将土体近似为分层土，误差较小;或近似为匀质的单一土层[2]，可以降低计算成本，但可能会有较大误差。因此，本文将基于反应位移法对两种地层地质结构处理方法进行比较分析。

1 地铁车站结构模型

以某一地铁车站为计算对象，车站横截面为一矩形，宽20m，高10m，顶板埋深5m。根据当地地形条件，地震作用的基准面在地表以下30m处。对于该车站的抗震设计，要求车站结构能够承受的地震烈度为9级（地震的重现周期为2475年）。

目前对地下结构进行抗震设计时，对于地层地质结构的处理主要由两种方法：（1）匀质单层土处理（单层土物理特性如表1所示）;（2）分层土处理，（此处分为3层，各土层物理特性如表2所示）。

2 计算参数

2.1 动力弹簧刚度

k=KLd

式中：k—动力弹簧刚度（kN/m2）;K—动力弹簧系数（kN/m）;L—地基中的弹簧间距（m）;d—土层沿隧道与地下车站纵向的计算长度（m）。

侧面土层的水平弹簧系数根据日本铁路抗震设计规范求解[3]：

K=1.7EoBh-3/4

式中：Eo—土层动变形模量;Bh—侧墙高度。

由模型与表1、2中已知的数据，求得各土层的动力弹簧参数，表3所示。

2.2 地层位移

地震时地层位移可简化为余弦函数[4]：

式中：u（z）—距地表面处为z处地震时的地层位移（m）; Su—地震动基准面速度反映谱（m/s）;TS—地震的固有周期（s）;H—地表至基准面距离（m）。

（1）地层固有周期TS：

式中：—土层厚度（m）;—剪切波速（m/s）。

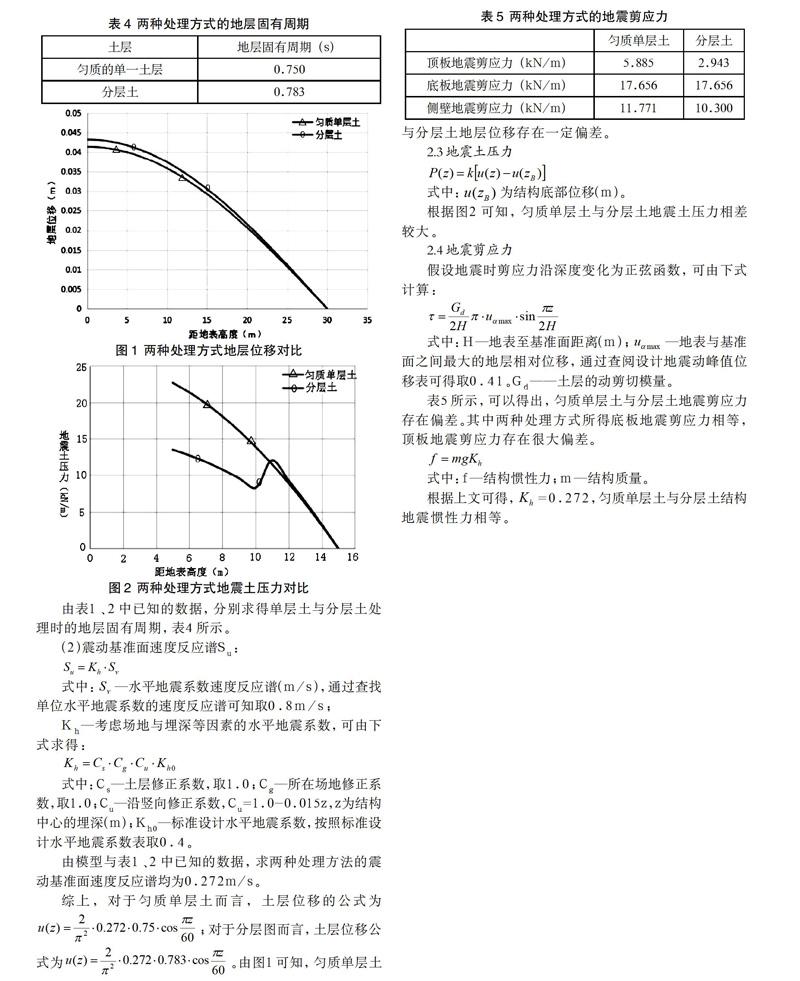
由表1、2中已知的数据，分别求得单层土与分层土处理时的地层固有周期，表4所示。

（2）震动基准面速度反应谱Su：

式中：—水平地震系数速度反应谱（m/s），通过查找单位水平地震系数的速度反应谱可知取0.8m/s;

Kh—考虑场地与埋深等因素的水平地震系数，可由下式求得：

式中：Cs—土层修正系数，取1.0;Cg—所在场地修正系数，取1.0;Cu—沿竖向修正系数，Cu=1.0-0.015z，z为结构中心的埋深（m）;Kh0—标准设计水平地震系数，按照标准设计水平地震系数表取0.4。

由模型与表1、2中已知的数据，求两种处理方法的震动基准面速度反应谱均为0.272m/s。

综上，对于匀质单层土而言，土层位移的公式为;对于分层图而言，土层位移公式为。由图1可知，匀质单层土与分层土地层位移存在一定偏差。

2.3 地震土压力

式中：为结构底部位移（m）。

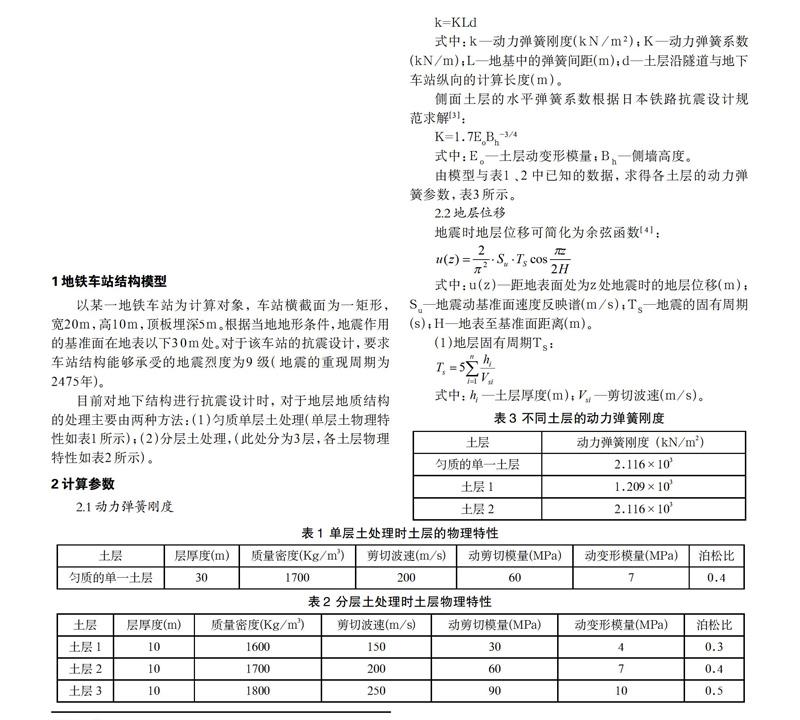
根据图2可知，匀质单层土与分层土地震土压力相差较大。

2.4 地震剪应力

假设地震时剪应力沿深度变化为正弦函数，可由下式计算：

式中：H—地表至基准面距离（m）;—地表与基准面之间最大的地层相对位移，通过查阅设计地震动峰值位移表可得取0.41。Gd——土层的动剪切模量。

表5所示，可以得出，匀质单层土与分层土地震剪应力存在偏差。其中两种处理方式所得底板地震剪应力相等，顶板地震剪应力存在很大偏差。

式中：f—结构惯性力;m—结构质量。

根据上文可得，=0.272，匀质单层土与分层土结构地震惯性力相等。

3 结语

在对地下结构进行抗震设计时，对于地层地质结构的处理主要由两种方法，即近似为分层土或匀质单层土处理。通过以上分析可知，两种处理方式得出的结构地震惯性力相等，但地层位移、地震土压力与地震剪应力偏差较大，其中地震土压力偏差尤为明显。因此在实际计算应用过程中应选用分层土处理的方式，更符合实际情况。本文仅基于反应位移法对两种底层地质结构处理方法进行了比较分析。在接下来的研究中，可进一步从自由场变形法、有限元反应加速法、时程分析法等设计方法入手进行比较分析。

参考文献

[1] 赵钊.反应位移法在地下结构抗震设计中的应用[D].中原工学院，2017.

[2] 王国波，王敏，覃程，高飞.对反应位移法中几个关键问题的探讨[J].地下空间与工程学报，2014，10（06）：1367-1371+1386.

[3] 施有志，华建兵，李秀芳，等.反应位移法在地下综合管廊抗震设计中的应用[J].吉林大学学报（地球科学版），2018，48（6）：1785-1796.

[4] 鄭学涛.基于反应位移法某地铁车站抗震研究[D].石家庄铁道大学，2015.