基于数学建模的集群运动模拟仿真研究

2019-05-08韩莉淼杨中元耿显亚

数学学习与研究 2019年6期

关键词：图论

韩莉淼杨中元耿显亚

【摘要】针对动物集群运动中鱼群的集群运动，通过仿真模拟，建立无差别个体的集群运动，优化Vicsek模型，在有领导者存在的群体中，利用离散数学中的图论建立鱼群中的信息传递网络，个体的运动受领导者的运动所影响，信息传递机制形成小世界网络，在此网络中信息传递快速，当次领导者的个数达到最优时，信息覆盖范围广，有利于鱼群的稳定.

【关键词】集群仿真模拟;小世界网络;Vicsek模型优化;图论

【基金项目】大学生创新创业项目（201710361095）支持.

集群是自然界中普遍存在的一种现象，动物在运动中经过自组织行为形成稳定的群体，研究表明集群行为对动物的生存有很大的益处，如有利于节约能量，理论计算表明，集群时所耗的摩擦力，大约只需要单独行动时的15;集群还有利于种群躲避捕食者，同时对种群的生殖、索饵和洄游中有很重要的意义[1].集群行为是一种动态稳定状态，也是通过个体以及局部的最基本的行为完成的复杂行为，对集群运动的研究，是仿生的重要组成，也具有重要意义.

根据Reynolds提出的Boid模型，知道鱼群运动所遵循的规则，但是模型存在一定的缺陷，它给出的规则都是局部规则，每个个体仅仅根据它周围附近区域内的个体行为调整自己的行为，只能做到局部一致性，局限性比较强，并且模型是在虚拟的、没有障碍存在的空间内进行模拟的，而实际中不可能没有障碍物.因此，提出Vicsek模型得出的鱼群的连通性与一致性[6]，来克服以上模型存在的缺点，而leading-following[8]模型中进一步提出了领导者在群体中的重要作用.根据领导者的存在，本文研究群体中的次领导者的信息传递，次领导者的数量对群体的影响.

一、无差别个体的集群行为仿真模拟

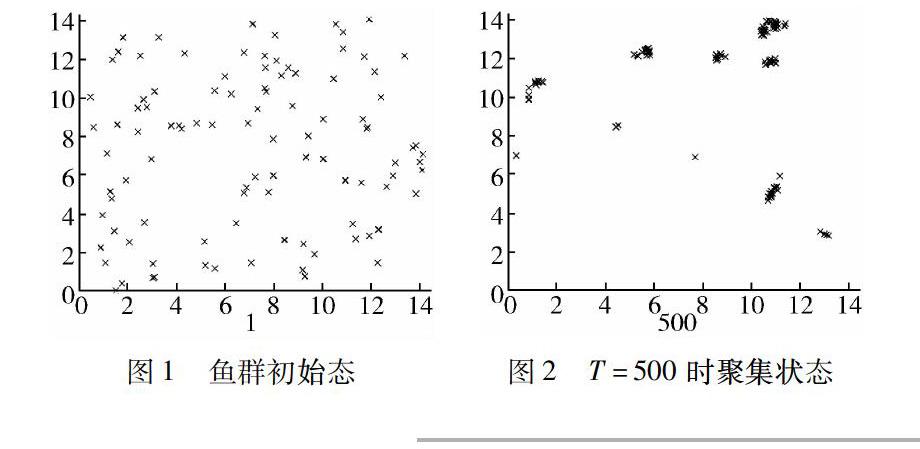
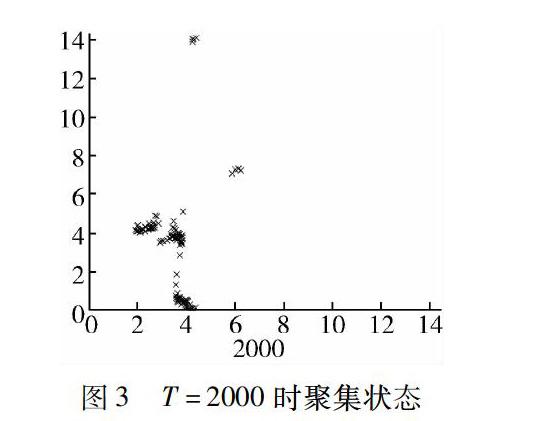
根据Boid模型中，鱼群的聚集原则：避免碰撞、速度匹配、中心聚集、惯性因素，利用Matlab设计迭代程序，模拟出散乱的鱼群，在不同时间的聚集程度，选取100个个体，设其初始速度为0.1，安全范围为0.2，通过不同时间的不同聚集状态，反映出鱼集群运动的过程[2].

从以上图中可以看出初始态鱼群分布散乱，时间为500时，鱼群中开始有小群体出现，时间为2000时，鱼群的聚集程度更加明显.

二、Vicsek模型优化

Vicsek模型是由N个具有自我意识的个体组成的离散时间系统，它们在平面中以大小相同的速率v运动，每个个体的角度按照邻居角度的矢量平均来更新，个体i的“邻居”由以该个体的当前位置（xi（t），yi（t））为中心，与该个体的Euclid距离小于正常数r的个体组成，用Ni（t）表示个体i在时刻t的邻居，即

Ni（t）={j|dij（t）

其中dij（t）=（xi（t）-xj（t））2+（yi（t）-yj（t））2，顯然，每个个体都是自身的“邻居”，每个个体在平面中按照恒定的正速率v运动，因而，每个个体的位置按照下面的方式进行更新：

xi（t+1）=xi（t）+vcosθi（t），yi（t+1）=yi（t）+vsinθi（t），i=1，2，…，N，

其中θi（t）为个体i在时刻t的角度，它按照下面的方式进行更新

θi（t+1）=tan-1∑jNi（t）sinθj（t）∑j∈Ni（t）cosθj（t）.

注意到上面系统的动态行为完全由初始状态、邻域半径r和运动速率v确定.进一步，每个个体的邻居由其他个体的位置决定，每个个体的角度由邻居的角度决定;同样，角度也会影响位置，因此，所有个体的位置和角度之间形成复杂的非线性关系，这使得问题的理论分析比较困难.

很显然，由Vicsek模型描述的多个体系统形成一个动态网络，图论中的一些基本概念对问题的分析是有帮助的，注意到每个个体的邻居会随时间而变化，Jadbabaie等人用无向图序列G={V，εt}来描述个体间的相互作用，其中V={1，2，…，N}为所有个体的集合，εr为随时间变化的边集合.边是这样形成的：如果个体i与j在时刻t的距离小于r，则在它们之间连一条边，记作（i，j）εr.一个连通图是指该图中的任何两个节点之间总存在一条路径.为方便分析，将上面公式写成下面等价的“拟”线性形式;

tanθi（t+1）=∑j∈Ni（t）cosθj（t）∑k∈Ni（t）cosθk（t）tanθj（t），

进而可写成矩阵形式为

tanθi（t+1）=A（t）tanθ（t），

其中tanθ（t）（tanθ1（t），tanθ2（t），…，tanθN（t））T，A（t）（aij（t））为加权平均矩阵，

aij-cosθj（t）∑k∈Ni（t）cosθk（t），若（i，j）∈εr，0，否则，

为分析Vicsek模型的同步性，Jadbabaie等人研究了公式的线性化形式

θi（t+1）-1ni（t）∑j∈Ni（t）θj（t），

其中ni（t）是集合Ni（t）内元素的个数.相应地，角度更新可写成下面的矩阵公式

θi（t+1）=A（t）θ（t），

其中θ（t）=（θ1（t），θ2（t），…，θN（t））T，矩阵A（t）称为平均矩阵，其元素为

aij（t）=1ni（t），若i与j在时刻t为邻居，0，否则，

通过此优化模型来进一步仿真鱼群运动.

三、小世界信息传递网络的构建

自然界中的群体通常有领导者的存在，鱼的集群运动会受领导者的运动影响，领导者有明确的运动方向和目的地，群体中还有次领导者的存在，次领导者可以预测领导者在下一时间阶段内的动态行为，然后根据判断在鱼群中传播信息，使群体行为保持稳定.

领导者与次领导者之间可以构成小世界网络，次领导者随机地分布在追随者之间，在以次领导者为圆心，r为半径的圆形区域内，追随者可以接收到次领导者传递的信息，调整运动状态，追随领导者的运动.

研究有领导者的鱼群的信息传递，采用构建信息传递网络的模型.一般的构建网络机制要用到图论中的有向图和无向图，引入离散数学的一些基本概念[7]：

一个有向图D是一个二元组（V，E），记为D=（V，E），其中：

（1）V是一个非空集合，其元素称为图的顶点（vertices）、结（节）点（notes）或端点;

（2）E是卡氏积V×V的多重子集，其元素称为图的有向边（简称边）（edges）或弧.

将鱼群的信息传递网络定义为

G={V，E，Cv，Ve，T}，（4）

其中V表示网络的结点集合，E表示边的集合，Cv，Ve分别为结点和边的集合，T为时间点的集合.则用结点表示鱼的个体，边表示个体之间的信息传递关系，不同的传递用有向图或无向图表示，本文中次领导者通过预测领导者的运动传递信息，追随者接收到次领导者传递的信息，以及自身感受到的邻居的信息，则追随者个体之间是否有信息交互，可以用表达式表示

bij=1，dij≤r，0，dij>r，（5）

bij=1表示有信息交互现象，bij=0表示无信息交互现象.

以△表示鱼群中的领导者，☆表示次领导者，○表示追随者，次领导者的信息传递范围用半径为r的虚线表示，在此范围外的追随者接收不到信息，△—△—表示次领导者对领导者的行为预测，构建下图所示信息传递网络.

四、次领导者最优数量模拟

以二維平面为例，有100个追随者随机均匀地分布在二维平面内，根据次领导者的数量以及信息传递范围，作代表追随者的点以及代表次领导者的信息覆盖范围的模拟图形，从图中可以看出次领导者的数量对整个范围的信息覆盖概率A，当然A越大，鱼群信息覆盖范围越大.

鱼群的次领导者存在最优数量，低于最优数量时，群体会由于信息传递网络不完整稳定性下降;高于最优数量时，信息传递范围会有过多交集，而在交集范围内的追随者接收到来自不同层次领导者传递的信息，信息之间会产生干扰，从而影响追随者的判断，导致群体的稳定性下降.

【参考文献】

[1]胡鹤永.鱼类集群行为及其优越性[J].海洋渔业，1988（3）：140-141.

[2]宋运忠，刘毛妮.基于改进智能体模型的群集运动行为研究[J].河南理工大学学报，2015（6）：818-825.

[3]余亚东，侯为根.二维空间中有唯一领导者的集群模型分析[J].安徽工业大学学报，2015（1）：72-75.

[4]李小雪.生命集群动态行为的预测机制研究[D].武汉：华中科技大学，2008.

[5]Reynolds C W.Flocks，herds，and schools：A distributed behavioral model[J].ACM SIGGRAPH Computer Graphics，1987（4）：25-34.