锚索应力增量法评价边坡稳定性

杨 敏，李 宁，李宏儒，李国锋

(西安理工大学岩土工程研究所，陕西西安 710048)

预应力加固技术是预应力混凝土技术在岩土工程领域的延伸与发展，是现代岩土工程中的一个重要分支。目前，预应力加固技术主要有预应力锚杆和预应力锚索。在1964年安徽省梅山水库在坝基岩体的加固中，首次成功使用了预应力锚索。预应力锚索加固岩体边坡的优势在于能为节理岩体边坡、断层、软弱带等提供一种强有力的“主动”支护，是所有传统非预应力的“被动”支护无法达到的。由于其预应力吨位大(30～1 500 t)，长度长(5～80 m)，具有其他锚固手段不具备的优点[1- 4]。从国内外研究现状来看，针对预应力锚索支护的作用机理、设计及施工方法等方面的研究已有很多，尤其在我国，预应力锚索支护被广泛应用，对该方面的研究也获得了很大进展。吴茂明等[5]以某一公路的滑坡治理为实例，详细介绍了预应力锚索在路堑边坡和地质条件复杂下的应用。叶海林等[6]采用振动台研究了预应力锚索轴力和预应力损失在地震作用下的动力特性、边坡在锚索支护下的整体稳定性。郑文博等[7]以西部某水电岩石高边坡为背景，应用有限元软件计算地震作用下的锚索内力分布、边坡位移及在最不利结构面组合下的边坡整体稳定性安全系数。赵炼恒等[8]基于岩土塑性极限分析上限理论的基本原理，考虑了预应力锚索的加固效应，分析了单、多预应力锚索加固措施条件下边坡的稳定性研究。Amini等[9]开发了一个可以进行块-弯曲倾倒稳定性评价的计算软件。 但对边坡预应力锚索锚固的稳定性评价研究非常少。

反倾层状岩质边坡为倾倒型破坏，没有明确的滑动面，用传统方法来计算其安全系数是不合理的。因此，本文基于数值仿真试验的研究，以边坡的锚索加固为主要研究对象，提出预应力锚索加固后的稳定性评价方法，然后结合某水电站左岸倾倒边坡的加固设计，并通过较为全面的数值仿真试验来研究不同锚索加固方案下倾倒边坡的稳定性，从而对大型水电岩质边坡的倾倒变形及预应力加固治理有更深刻的认识。

1 边坡预应力锚索稳定性评价方法

图1 锚索单元几何模型[10]Fig.1 Sketch map of geometric model of anchor cable element[10]

预应力锚索的模拟采用 FINAL 分析系统中经过一些特殊处理后的特殊锚索单元，该单元可以分别模拟自由段、锚固段以及反映锚索与围岩相互作用。单元由4个节点构成[10](见图1)，其中节点1和2为孔壁上两角点，节点3和4在锚索体上，为锚索两个端点，节点1与3，2与4分别具有相同的坐标。在生成有限元网格时，节点1-3，2- 4代表锚索单元与岩体的实体单元相连。

模拟预应力锚索施加过程如下：预应力锚索施加时，激活预应力锚索单元，使锚固段处锚索单元的节点与实体单元的节点位移相耦合，在锚头处对锚索施加张拉力，同时预应力锚索锁定后，锚墩对坡体的压力通过对坡体施加反向压力来实现。在边坡的后续开挖过程中，再将锚头处锚索单元的节点与实体单元节点耦合锁定。采用这种方法来模拟预应力锚索，充分考虑了预应力锚索在实际工程中的施工过程，真实地模拟了预应力锚索的锚固段、自由段和锚墩，充分反映了锚索的预应力和刚度对边坡应力场、位移场的影响。

李宁等[10]对预应力锚索的自由段模拟仍采用集中力模型，即在锚索自由段两端节点上加一对等值反向的作用力(或锚头处采用均布力反压)。根据开挖台阶不断下切，预应力锚索的刚度作用采用应力补偿方法实现，即后续补偿力通过数值仿真分析出围岩锚固后在外荷载下的变形，然后再利用这一变形反算出补偿力增量，在下一次边坡开挖中用“附加预应力”来模拟。基本假定预应力锚索对围岩刚度影响忽略不计，则后续开挖后，锚索处的新增变形引起的锚索预应力增加Δσ：

Δσ=(ΔL/L)EA0

(1)

式中：ΔL为锚索两端的位移差；Δσ为各工况下锚索的变形量ΔL引起的锚固应力增量；A0为锚索的有效横截面面积；E为锚索的弹性模量；L为锚索的原长度。

在考虑了预应力锚索的作用后，边坡岩体的力学性能得到改善，从而引起边坡的受力状态发生变化，此时如仍按一般边坡稳定性评价方法评价并不合理。现有预应力锚索支护边坡设计方法中，或不考虑预应力，或提高岩质边坡的c,φ值，这些处理方法都不够合理[11- 12]。由于岩体应力、变形状况往往缺乏明确的安全标准，因此预应力锚索安全状况对判断整个加固岩体的安全性起着至关重要的作用。本文在李宁等[10]提出的后续张拉补偿法的基础上，提出采用支护结构的受力特性来表征边坡体的稳定性，即用预应力锚索在各工况下产生变形所引起的应力增量与允许应力增量的差值，将该差值与允许应力增量的比值称为稳定系数，该稳定系数K可描述如下：

(2)

式中：σ为预应力锚索的设计张拉应力。

2 某水电站左岸坝轴线边坡锚索加固稳定性分析

2.1 工程概况

某水电站左岸边坡片麻理层间可见云母条纹和长石、石英细脉的起伏弯折和定向排列。片麻理属于一种不连续结构面，当黑色矿物(云母和角闪石)沿片麻理局部富集，极易在岩石中产生蚀变带，从而影响坝址区周围岩体的质量。片麻理的产状为：走向NE3°～24°，倾向NW(个别SE)，倾角∠72°～85°，垂直坝轴线陡倾右岸(河道)。从现场钻孔的勘探岩心鉴定来看，深部发现有断层带物质存在，岩心破碎成细粒到中粒砂，这种迹象不能排除存在陡倾角断层的可能；岩体中主要发育两组构造裂隙：一组缓倾裂隙，产状NW340°，倾向NE，倾角∠9°；另一组陡倾裂隙，产状NW285°～290°，倾向NE 或者 SW，倾角∠70°～81°。裂隙宽度多在1～3 mm之间，少量钙质充填，发育间距大，密度小，裂面平直粗糙或起伏粗糙，可见延伸长度10～15 m。偶尔可见一些其他方向的随机节理(或裂隙)。这些软弱结构面与片麻理组合，可能在坝基开挖过程中相互切割形成局部不稳定块体，应注意加强支护。因此，该边坡天然岸坡高(大于80 m)、自然坡角大(大于50°)、片麻理陡倾岸外(倾角大于81°)，加上与片麻理垂直的陡倾裂隙和平缓裂隙，是导致该部位岩体产生卸荷、倾倒和坍塌而形成崩积体的主要原因。

2.2 有限元分析模型建立

根据地质分析，边坡地质模型可概化为：残积土、强风化、中风化和微风化共4种岩土体，由于离散化有限元FINAL中结构面单元的局限性， 因此建立结构面分布合理的二维数值分析概化模型如图2所示。二维地质模型范围平行于滑体主轴方向为120 m (X轴方向)，边坡后缘垂直于滑体主轴方向为105 m (Y轴方向)。坐标系为水平向由左岸向右岸为正，垂直向上为正。边界条件下部为位移全约束，左、右两侧施加法向位移约束，上部为自由边界。该区域构造应力场较小，不予考虑，只计算重力场。坡面在自然状态下为自由边界。分析中有限元模型包括围岩单元(LST 单元)、开挖单元(LST 单元)及软弱夹层单元(COJO 单元)，数值试验中岩体(围岩和开挖部分) 采用Mohr-Colunmb 强度准则。

图2 数值分析概化模型及坡表关键点Fig.2 Generalization model of numerical analysis and key points of slope table

根据岸坡边坡内岩体的倾倒、挤压破碎的产状，运用非线性摩擦型界面接触单元(COJO 单元)来模拟岩体倾倒的层面性状；运用非线性摩擦型界面接触单元(COJO 单元)包裹实体单元(LST 单元)来模拟岩体的破碎性状，该方法既能反映岩组合体与倾倒岩层的变形特征，又能反映破碎块体的滑移特性。

为了更加清楚地对岸坡的变形及稳定性进行分析，在岸坡坡表从上至下选取了15个关键点，坡表关键点布置如图2所示。

2.3 岩体及结构面计算参数

依据室内试验资料，综合分析岩石物理力学指标试验值及物探波速测试成果，并类比参考其他工程岩体力学试验成果，在岩体质量分级的基础上，提出不同岩土体及工程区结构面的力学参数。

由于本工程地质条件复杂、边坡的相关力学参数不易确定，根据相关设计院所提供的基本参数范围和工程现场多点位移计测值进行相关参数确定，所得岩土体及边坡结构面力学参数如表1和2所示。

表1 边坡岩体参数

表2 结构面参数

2.4 影响因素数值模拟加载方式

在进行数值模拟时，根据设计院提供的参数，最大可信地震加速度(MCE)为0.280g，基本运行期地震(OBE)为0.175g。计算中水平地震加速度取为峰值加速度的2/3(即MCE水平地震加速度取为0.187g，OBE水平地震加速度取为0.117g)，竖向地震加速度取为水平向地震加速度的2/3。地震作用力用拟静力法模拟。施加方式采用体积力的方式进行施加。拟静力体积力按计算，其中ρ为岩土体密度，V为体积，a为地震水平加速度。

对于暴雨工况的模拟，考虑到边坡在遭遇连续7天以上强降雨时，边坡表层岩体由非饱和态转为饱和状态，所以取重度为饱和重度；在降雨作用下，坡体部分岩体软化，从而造成裂隙面上岩体或充填物抗剪强度降低，本文从简化和安全的角度考虑，认为坡体浸润线以下的岩体强度为上部岩体的80%。由于暴雨使得裂隙快速饱和，考虑到裂隙从上到下被水充满且对裂隙产生压力，对此不利工况的边坡稳定性进行分析。

2.5 预应力锚索设计加固方案

根据坡体的环境条件，拟定了3种计算工况，分别为自然工况、降雨工况和地震工况。不同计算工况下，对边坡采用3种不同锚索设计加固方案进行稳定性分析，不同方案所采用的锚索根数、间距及方向有所不同。加固方案针对坝基处采用锚杆加固，对坝基以上即1 493 m高程以上岩体采用预应力锚索加固，单根锚索的锚固力均为1 000 kN，每根锚索长度均为60 m，不同预应力锚索加固方案如图3所示。

图3 各锚索加固方案

2.6 各工况各设计加固方案变形分析

不同设计加固方案时各工况下边坡坡表关键点的水平位移见图4。

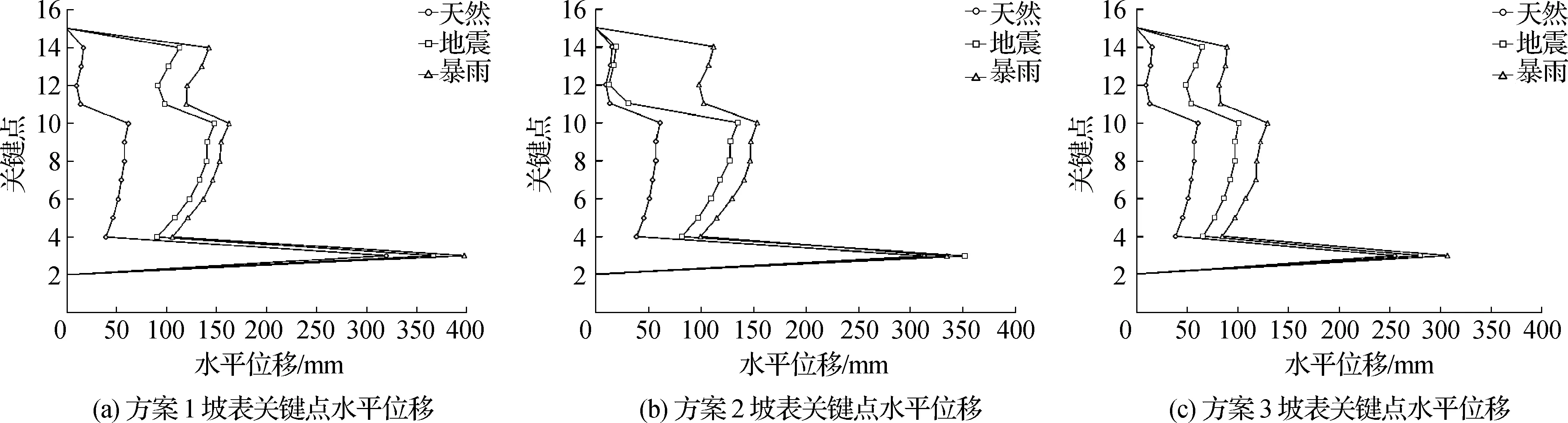
图4 各方案坡表关键点水平位移曲线

从图4可以看出：各方案坡表关键点的位移变形规律大体一致。坡表关键点的位移在天然工况下最小，在暴雨工况下最大。从整体上来看方案3坡表关键点的位移规律性较好，位移量也较小。各方案下坡表上关键点3的位移最大，这是由于关键点3处于结构面交互软弱部位，有剥落的可能。此外，边坡中高程关键点10和上部关键点14的位移也较大。总体而言，边坡中高程点的位移相对较大，这是由于该边坡是反倾层状岩质边坡所致。

2.7 加固方案稳定系数分析

根据本文提出的边坡稳定系数计算式计算各工况下不同设计加固方案时边坡的稳定系数，计算中采用锚固力F为1 000 kN，弹性模量E为195 000 MPa，抗拉强度为1 860 MPa级预应力锚索。3种方案下各种工况每根锚索的稳定系数见表3。

表3 各工况下锚索的稳定系数

从表3可以看出，方案1在边坡中高程部位设置了10根锚索进行锚固，天然工况下每根锚索的稳定系数均为2.0，说明在天然工况下边坡是稳定的；暴雨工况下，1～6号锚索的稳定系数都小于1.0，且稳定性最小的为锚索1，这10根锚索的平均稳定系数为0.95，说明在这种工况下，边坡处于危险状态；地震工况下，除第1号锚索的稳定系数小于1.0外，其余锚索的稳定系数都大于1.0，这10根锚索的平均稳定系数为1.17，可见在这种工况下，边坡相对稳定。综合考虑认为，采用方案1加固时边坡处于不利稳定状态。

方案2在边坡中高程部位设置了14根锚索进行锚固，锚索间距作了调整。从表3可以看出，天然工况下每根锚索的稳定系数均为2.0，说明在天然工况下边坡是稳定的；暴雨工况下， 1～2号锚索的稳定系数都小于1.0，且稳定性最小的为锚索1，平均稳定系数为1.07，可见该工况下边坡处于临界破坏状态；地震工况下，这14根锚索的平均稳定系数为1.56，稳定性最小的锚索为8，其值为1.21，稳定性最大的是锚索5，其值为1.96，可见该种工况下边坡相对稳定。综合考虑认为，采用方案2加固时边坡处于临界破坏状态。

方案3中锚索的角度作了调整，均为水平方向加固，锚索间距和方案2相同，采用了12根锚索。从表3可以看出，各工况下所有锚索的稳定系数均大于1.0。说明采用方案3加固时边坡处于稳定状态。对于反倾层状岩质边坡而言，锚索水平加固对边坡的稳定最有利。

2.8 最危险工况各加固方案分析

根据以上关键点位移及边坡稳定系数计算的结果，可知暴雨工况最危险，故对各方案在暴雨工况下进行变形分析(图5～7)。

图5 各方案暴雨工况的变形

从图5可以看出，各个方案的变形有明显的倾倒趋势，方案1的变形最大，且有破坏的趋势，这与边坡稳定系数的计算结果相一致。方案2和方案3的变形大致相同，第1条裂缝为拉裂，中高程坡表岩体有倾倒趋势，各条拉裂缝出现不同程度的拉开，坡脚处拉裂缝出现弯折剥落现象。

图6 各方案暴雨工况的位移

从图6可以看出，方案2到方案3的位移量逐渐减小，与前文关键点的位移规律大致相同，在坡角优势结构面处的位移最大，方案3中高高程最大位移约为90 mm，中高程最大位移约为120 mm，坡脚处的最大位移约为310 mm。

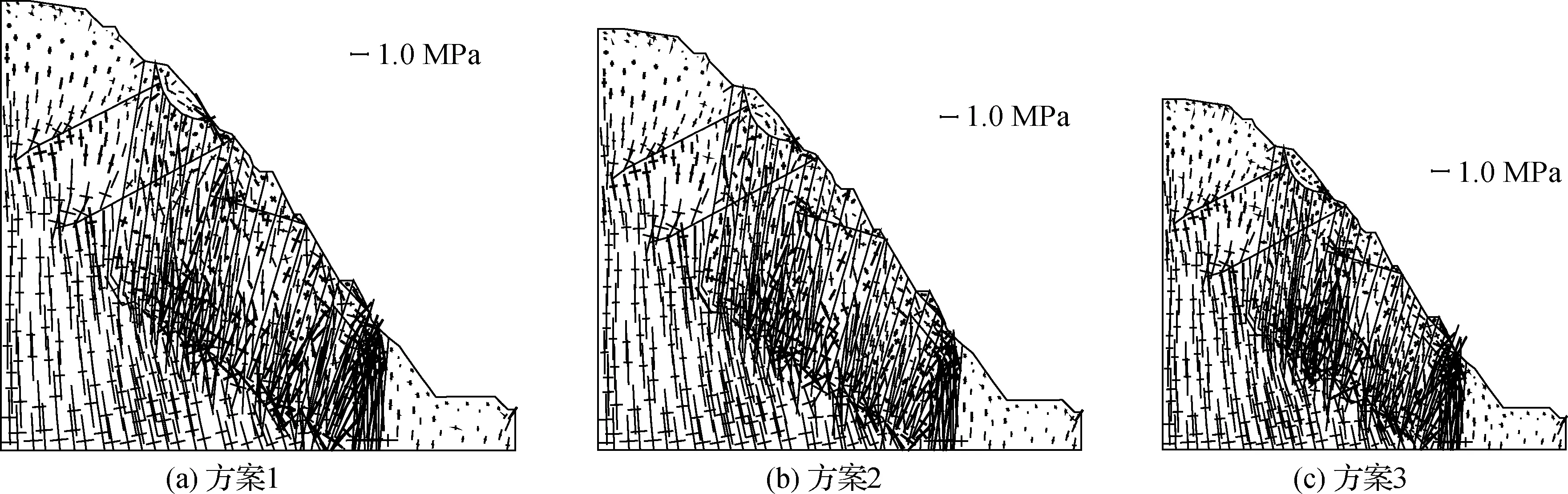
图7 各方案暴雨工况的应力

从图7可以看出，方案1的拉应力分布范围较广，坡角和裂缝底部出现大范围的应力集中现象。3种方案的应力场都是在坡脚处出现应力集中，拉应力分布范围较大；在后缘两条反倾裂隙处均出现部分拉应力；在中高程裂缝集中的部位有多处拉应力。方案 3中后缘反倾裂隙处的最大拉应力为0.55 MPa，坡表最大的拉应力为0.2 MPa，拉裂缝集中部位的最大拉应力为1.1 MPa，坡脚处的最大应力为1.3 MPa。由此来看，暴雨工况下边坡的稳定性比较差。

通过对3种设计加固方案下边坡稳定性的对比分析，建议采用第3种加固方案，即下5根间距5 m×5 m和上7根间距4 m×4 m，单根100 t，长度60 m预应力锚索组进行水平向加固。

3 结 语

预应力锚固效果直接关系到倾倒边坡的稳定性，采用离散化的有限元方法对锚索加固工程进行了数值模拟分析研究。首先，提出采用支护结构的受力特性来表征预应力锚索加固后边坡的稳定性，具体是指用预应力锚索在各工况下产生变形所引起的应力增量与允许应力增量的差值，将该差值与允许应力增量的比值来表示边坡稳定性。其次，通过对某水电站左岸坝轴线边坡锚索加固稳定性数值模拟分析得出：通过本文提出的边坡稳定系数计算方法所得到的边坡稳定性状况与边坡的应力场、位移场及变形场的结果一致；从3种预应力锚索加固方案的对比来看，锚索水平向加固对反倾层状岩质边坡的稳定性最有利。