改进的非线性时变增益模型在辽宁北部中小河流洪水模拟中的适用性分析

陈祖辉

(辽宁省铁岭水文局，辽宁 铁岭 112000)

当前，中小河流洪水呈现频发、多发的态势，中小河流的防汛工作越来越关键，中小河流洪水模拟是中小河流防汛决策的关键。近些年来，中小河流洪水模拟逐步成为研究热点，取得一定研究成果[1- 6]，其中时变增益模型综合考虑流域降雨径流的非线性理论，在中小河流洪水模拟中取得良好的模拟效果[7- 9]，但传统的时变增益模型未考虑降雨强度对洪水模拟的影响，因此在一些短历时强降水影响下的中小河流洪水模拟存在一定的局限，为此，夏军[10]院士对传统的时变增益模型进行改进，引入降雨强度因子，进一步提升了模型对中小河流洪水模拟精度的影响，改进的非线性时变增益模型在辽宁西部地区得到了应用，但是在辽宁北部地区的适用性还未进行相关讨论，为此本文引入改进的非线性时变增益模型，以辽宁北部某中小河流为研究实例，探讨该改进模型在辽宁北部中小河流洪水模拟的适用性。

1 研究方法

流域降雨径流是非线性变化过程，产流过程中包含的要素为降雨、蒸发以及流域蓄水量的变化，日尺度过程下的水量平衡方程为：

Y(d,n)=X(d,n)-L(d,n)

(1)

L(d,n)=E(d,n)±ΔS(d,n)

(2)

式中，X(d,n)—日降雨量，mm；E(d,n)—日蒸发量，mm；n—年尺度；ΔS(d,n)—流域蓄水量的变化量，mm；Y(d,n)—增量函数；L(d,n)—损失函数。

在计算中，模型需要计算流域的产流系数G，其计算方程为：

(3)

式中，所有变量同方程(1)和(2)中的变量含义。

在模型产流计算中主要计算场次降雨下的净雨量，其计算方程为：

R(t)=G(t)X(t)

(4)

式中，G(t)—模型产流系数值。

模型在计算产流量时还需要计算流域前期土壤含水量API，该变量与流域前期土壤含水量之间有着非线性变化关系，计算方程为：

G(t)=g1g2API(t)

(5)

式中，g1和g2—模型增益参数。

API(t)可以采用以下方程进行计算：

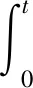
(6)

式中，U0(σ)—卷积响应函数。

在流域汇流模拟中采用较为简单的非线性响应函数进行分析，汇流计算方程为：

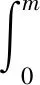
(7)

式中，U(τ)—系统响应函数。

2 研究结果

2.1 流域概况

本文以辽宁北部某2条中小河流为研究实例，集水面积分别为328.6km2及729.3km2，两个流域内的年平均降水量为650mm，两条中小河流有较为连续的水文监测数据，近些年来，两个流域内发生较为明显的洪水过程，因此选择这两个流域为典型流域，基于两个中小河流区域10场洪水数据，结合改进前后的时变增益模型，对流域的洪水模拟精度进行对比分析，从而分析改进前后的非线性时变增益模型在辽宁北部区域洪水模拟的适用性。

2.2 模型参数设置

对两个流域的模型进行参数设置，模型参数设置结果见表1和表2。

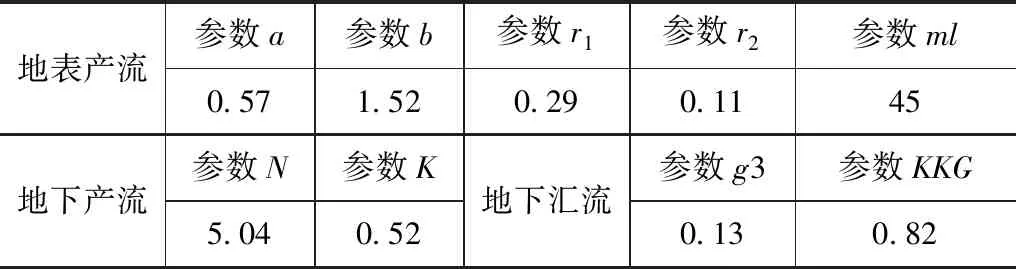
表1 1#流域场次洪水改进时变增益模型参数设置表

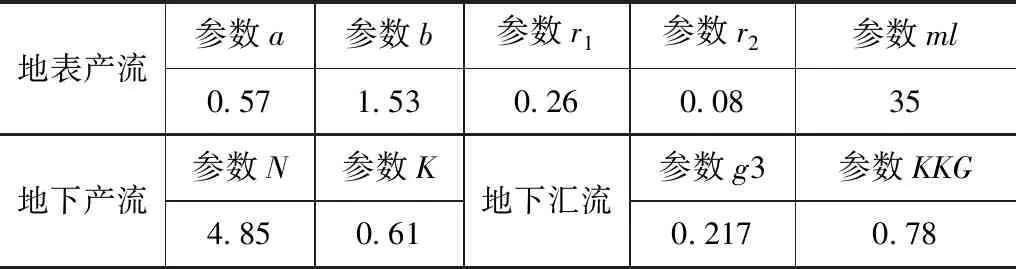
表2 2#流域场次洪水改进时变增益模型参数设置表

2.3 模拟结果

分别结合改进前后的时变增益模型对两个流域的洪水模拟精度进行适用性分析，分析结果见表3—4，如图1—2所示。

(1)1#流域适用性分析结果

从表3中可以看出，改进前后的非线性时变增益模型较传统模型在确定性系数、径流深相对误差、洪峰误差上均有一定程度的改善，从分析结果可看出，确定性系数上，改进后的非线性时变增益模型的确定性系数均值较改进前提高0.20，而径流深相对误差合格率提高50%，10场洪水洪峰误差合格率提高幅度较小，为10%。在洪峰出现时间误差上，改进前后的非线性时变增益模型合格率为100%，两个模型在洪峰出现时间误差上均较好地满足精度要求。从图1对比结果可看出，改进后的非线性时变增益模型由于综合考虑暴雨强度影响，吻合程度好于传统的非线性时变增益模型。

(2)2#流域适用性分析结果

从2#流域洪水模拟对比精度可看出，改进前后的非线性时变增益模型较传统模型在确定性系数、径流深相对误差、洪峰误差上也同样有一定程度的改善，从分析结果可看出，确定性系数上，改进后的非线性时变增益模型的确定性系数均值较改进前提高0.26，而径流深相对误差合格率提高30%，低于1#流域的径流深相对误差合格率，10场洪水洪峰误差合格率提高幅度较小，为30%，高于1#流域洪峰误差模拟精度。在洪峰出现时间误差上，改进前后的非线性时变增益模型合格率为100%，两个模型在洪峰出现时间误差上均较好地满足精度要求。从图2对比结果可看出，改进后的非线性时变增益模型由于综合考虑暴雨强度影响，吻合程度好于传统的非线性时变增益模型。

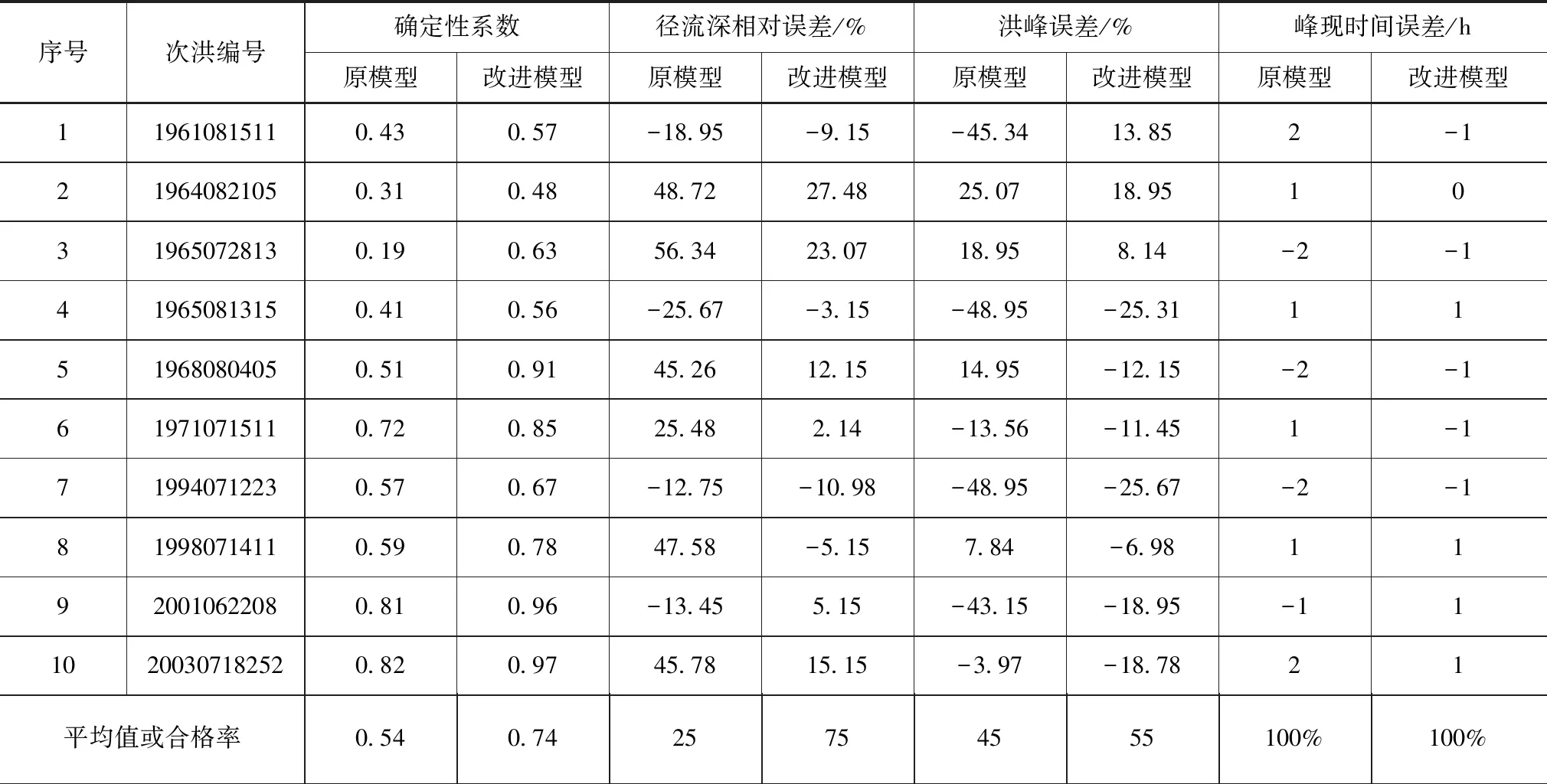
表3 1#流域时变增益模型率定期结果特征值表

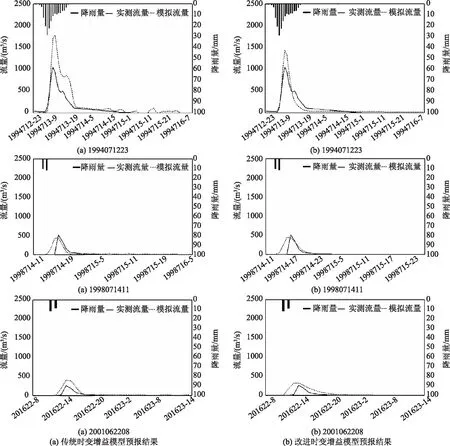
图1 1#流域时变增益模型验证期洪水预报过程

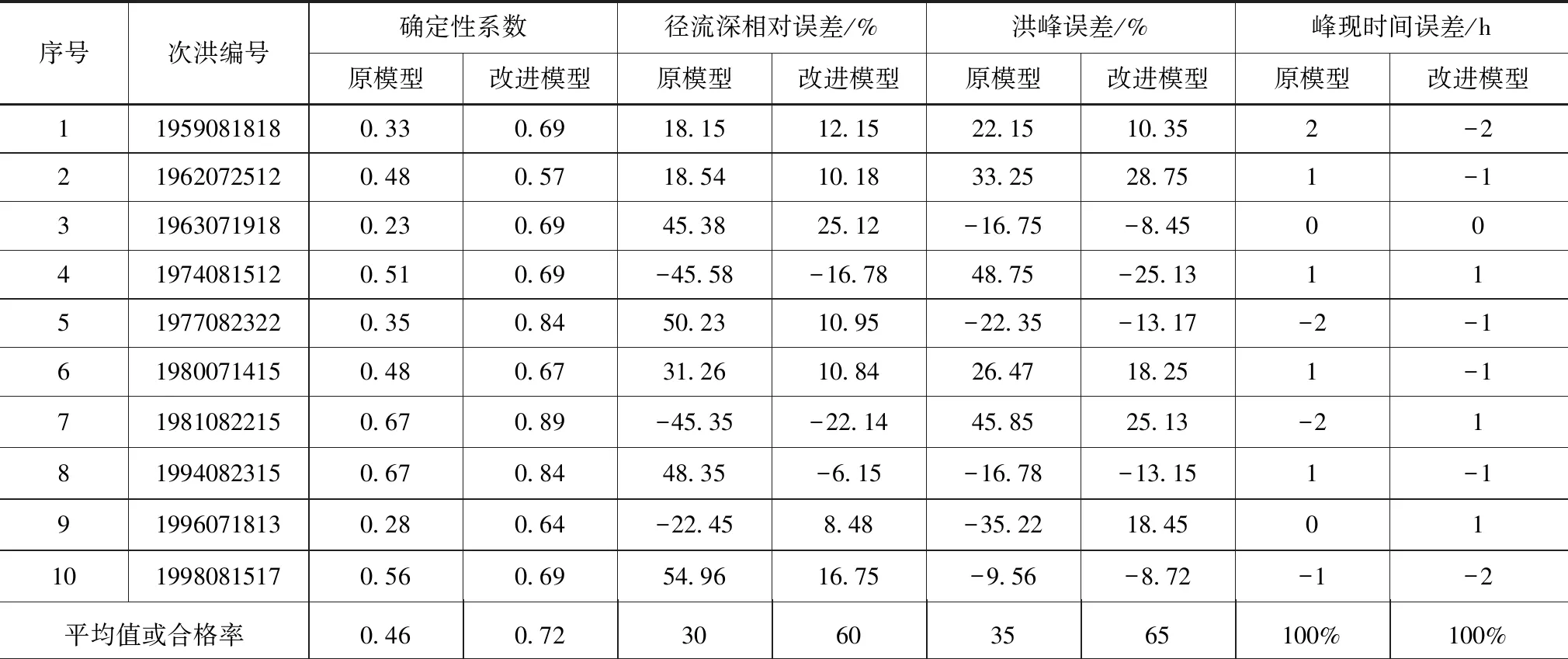
序号次洪编号确定性系数径流深相对误差/%洪峰误差/%峰现时间误差/h原模型改进模型原模型改进模型原模型改进模型原模型改进模型119590818180.330.6918.1512.1522.1510.352-2219620725120.480.5718.5410.1833.2528.751-1319630719180.230.6945.3825.12-16.75-8.4500419740815120.510.69-45.58-16.7848.75-25.1311519770823220.350.8450.2310.95-22.35-13.17-2-1619800714150.480.6731.2610.8426.4718.251-1719810822150.670.89-45.35-22.1445.8525.13-21819940823150.670.8448.35-6.15-16.78-13.151-1919960718130.280.64-22.458.48-35.2218.45011019980815170.560.6954.9616.75-9.56-8.72-1-2平均值或合格率0.460.7230603565100%100%

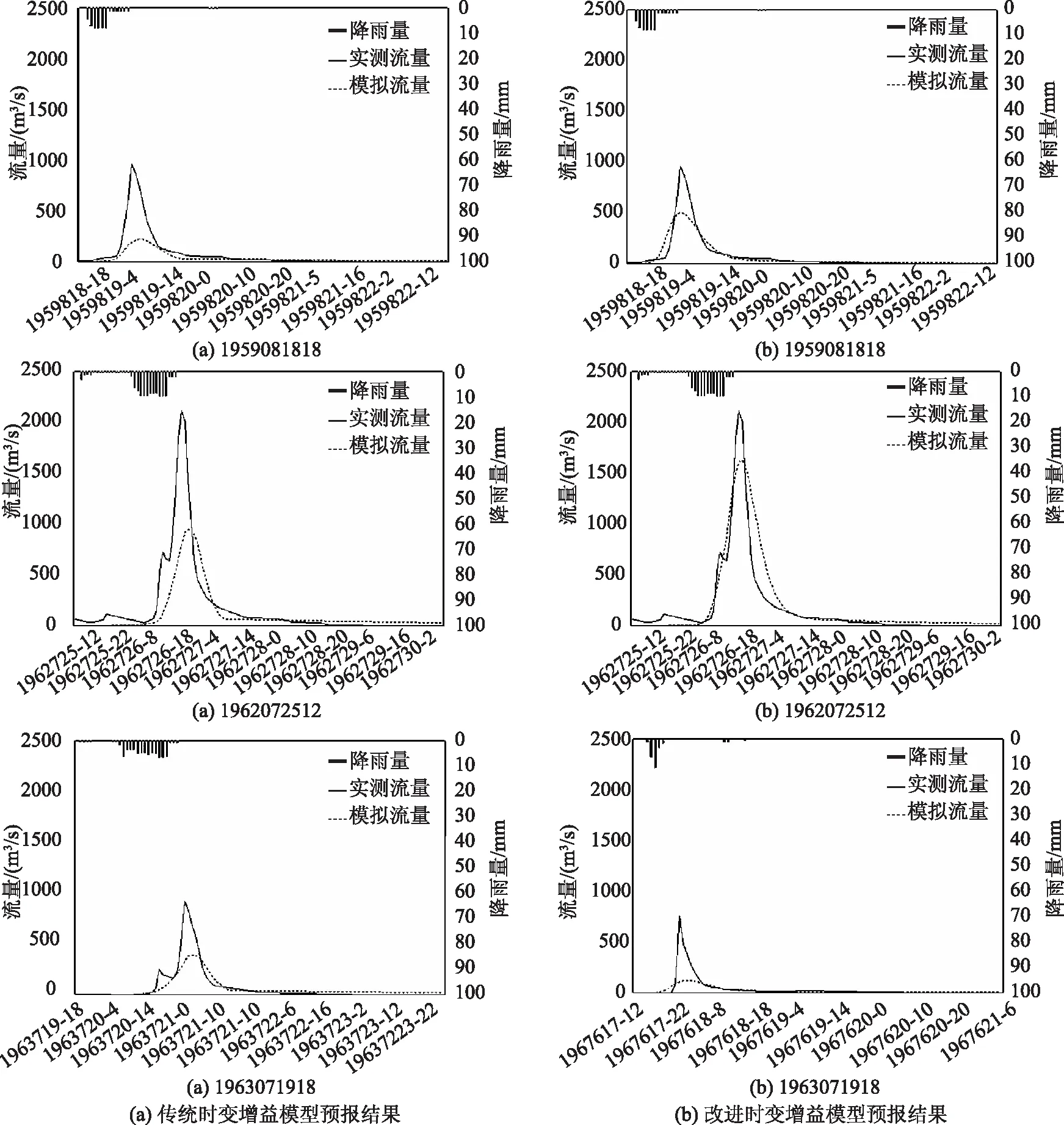
图2 2#流域时变增益模型率定期洪水模拟过程

3 研究结论

(1)改进的非线性时变增益模型，由于综合考虑暴雨强度，更适合于中小河流暴雨洪水历时短的特点，因此在中小河流洪水模拟精度具有较好的适用性，可以进行相应的推广和应用。

(2)在辽宁地区，具体应用改进的非线性时变增益模型时应重点关注地下水的两个参数，其参数敏感程度均较高。

(3)本文只选取了两个典型流域进行分析，在以后的研究中还需要加入更多的中小河流进行洪水模拟的适用性分析。