一种基于CORDIC算法的改进型DDS设计
2019-05-08崔乔冬王堂胜周彭宇杜滨媛
黄 玮,崔乔冬,王堂胜,周彭宇,谢 帅,杜滨媛
(江苏信息职业技术学院,江苏 无锡 214000)
0 引 言
DDS即直接数字频率合成技术,由美国学者J.Tiercy,M.Rader和B.Gold于1971年首次提出[1]。其结构主要包括相位累加器、只读存储器、数模转换器和低通滤波器等。相对于第一代直接模拟频率合成技术和第二代间接频率合成技术来说,DDS技术具有频率分辨率高、低功耗、速度快等优点。
DDS的设计方法有多种[2]。传统的查找表法结构简单,易实现,但精度较低,需要较大的ROM容量。多项式近似法对存储容量的要求较低,精度较高,但电路结构复杂,工作速度较慢。CORDIC算法采用简单的移位操作替代了原来复杂的计算,提升了计算速度,并能在存储容量要求不高的情况下获得较高精度。
DDS可以装载并寄存用户存入的频率控制码,根据控制码进行相位累加,根据相位大小得到不同的电压幅度,实现相位-幅度转换。此时得到的一般是数字化的正弦波,还需要通过数模转换器和低通滤波器得到可应用的模拟信号,即用户所需的频率。
1 DDS系统结构
一个典型的DDS系统结构(如图1所示)通常包括四个部分[3],分别为相位累加器(PA)、相幅转换器(ROM)、数模转换器(DAC)和低通滤波器(LPF)。其中,相幅转换器是系统中最核心的部分,可以将相位转换为幅度,对整个DDS的影响最大,是本次设计的重点。
实现相幅转换器的方法有很多,包括查找表法、泰勒级数近似法等[4],但其对存储容量、计算精度等方面的需求无法满足。CORDIC(Coordinate Rotation Digital Computer)算法采用坐标旋转,可以计算三角函数、双曲函数等基本功能函数。其通过加法运算、数据移位和迭代等基本操作实现函数计算。由于不需要乘法、除法等相对复杂的运算,因此不需要太多的存储空间,且相应的电路结构不复杂,完全适用于DDS系统设计。
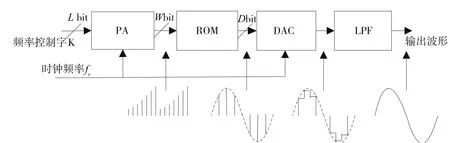
图1 DDS结构原理
2 CORDIC算法的改进
CORDIC算法有两种运算模式[5],即旋转模式和向量模式。本文中采用旋转模式,设定基数,再通过一系列运算,实现角度的不断调整,进而不断逼近设定的旋转角度。
传统的CORDIC算法实现主要有循环迭代结构和流水线迭代结构两种。循环迭代结构借助二选一的数据选择器,不断将计算结果输入迭代结构,通过多次循环获得所需值,所需存储容量小,但每次只能进行一个运算,工作速度慢。而流水线结构可以使电路在时钟周期内执行运算,运算量大,大大提升了工作效率。
为了达到简化电路结构、节省存储空间的目的,在传统CORDIC算法的基础上进行了改进,采用三角函数近似变换,使传统CORDIC算法计算每次迭代的存储角度时更为简单。混合CORDIC算法结构图如图2所示。
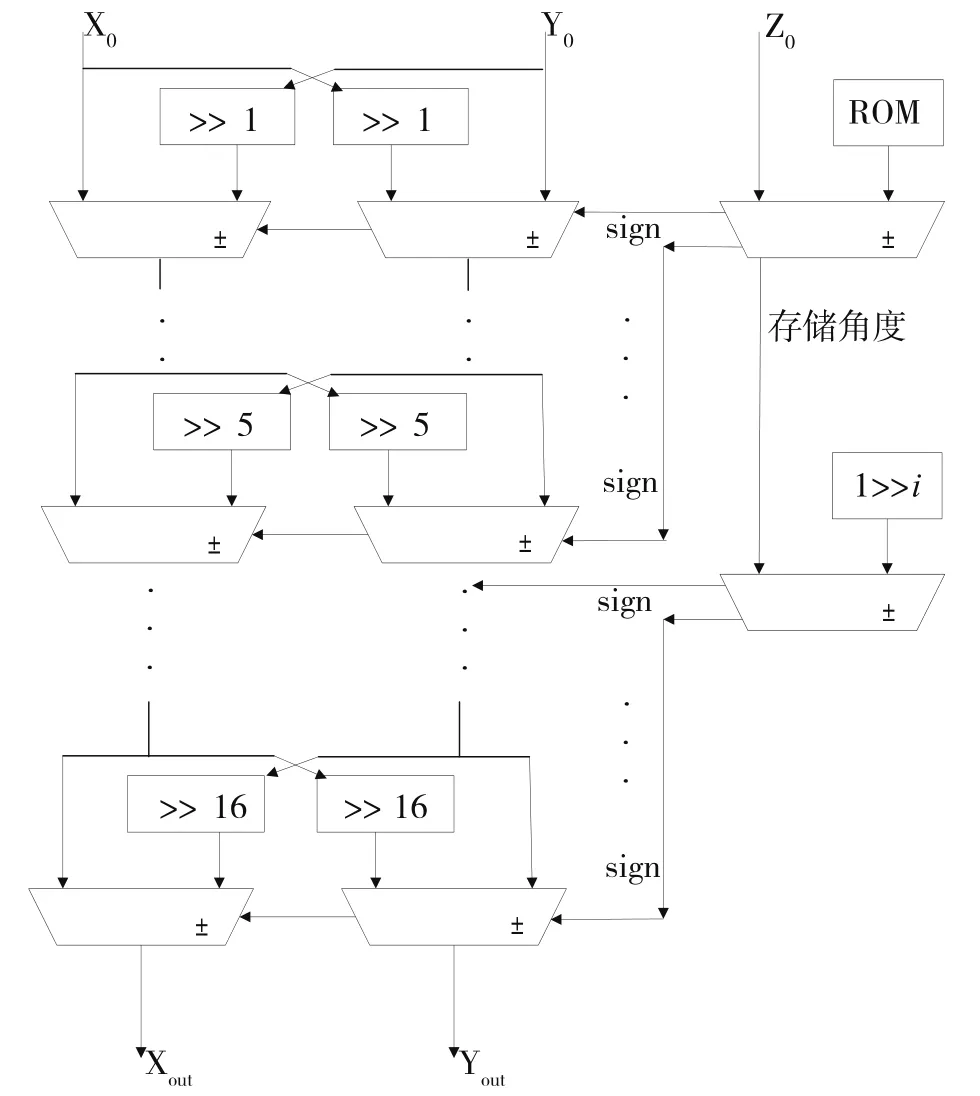
图2 混合CORDIC算法
CORDIC算法中总的输入旋转角度θ可以由一系列二进制数近似线性表示:

其中,∂i∈{-1,1},当∂i为1时,角度沿逆时针方向旋转;当∂i为-1时,角度沿顺时针方向旋转,δ为角度近似误差,满足δ<2-i,且2-i应尽可能小,以最大程度减小近似误差。计算过程中,每次迭代存储时的输入角度为arctan2-k-1arctan2-k-1(其中k=0,1,2…)。当k足够小时,arctan2-k-1≈2-k-1,如此一来,为了获得所需要的精度,CORDIC算法中最后一次旋转的角度需要小于2-i。
迭代计算过程中,不需要每次重新输入。利用正余弦函数的对称性,通过折叠象限,系统只需改变输入角度区间内的初始相位,便能得到整个2π象限的正余弦函数值,从而可以确定区间的输入。各区间所对应的输入值如表1所示。
为了实现16位的系统精度,至少需要16位的字长,对于[0,π/4]内任意输入的16位精度的任意角θ,可用二进制表示法表示:

其中,bi为符号位,bi∈{0,1},进一步化简为:
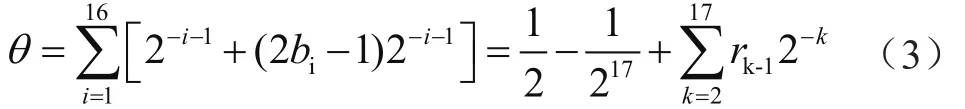

表1 各区间所对应的输入值
其中,rk-1=2bi-1∈{-1,1}。由于精度要求16位,因此可将式(3)中的1/217项忽略,则为:

式(4)中,如果θ2所对应部分的迭代次数超过5时,可以用2-k代替arctan(2-k),采用加法运算和移位等方式,从而轻松成多次迭代运算,节省了系统的存储资源。此外,θ1可改写为:


考虑到误差需要进行变换,将θ1改写为:

计算后发现,5次迭代后的误差较小,不影响运算精度,如式(8)所示:

因此,可以直接转换为二进制系数表示之前的旋转方向,但ε'表示的近似误差不能忽略。一般可将误差合成,形成新的θ2':
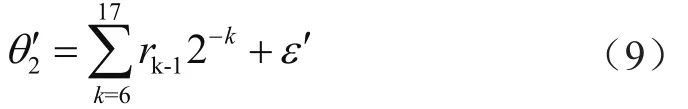
依据上述步骤进行反复推导,最终确定θ2部分的旋转方向。但是,这种做法中的近似误差需要进行额外计算,电路复杂度较高。若根据前次迭代的旋转方向,预测每次迭代后的结果,虽然可以预测所有迭代的旋转方向,但是存在误差,仍需设置专门的电路模块,比如进位保留加法器或超前进位加法器,增加了系统电路的复杂度。
为此,本文进行了以下改进,不再专门计算误差,而是将前面迭代后的剩余角度都存入ROM,作为第5次迭代的角度输入,与2-i(i≥6)进行比较,如此就无需计算近似误差值ε'。改进后的结构示意图如图3所示。
改进算法根据输入角度确定后续四次的迭代方向和相应的剩余角度,并由2-k直接代替arctan(2-k)确定剩余迭代的旋转方向,从而完成所有迭代运算。

图3 改进后的CORDIC算法
3 结 论
相幅转换器是DDS结构的核心部分,本设计采用了CORDIC算法实现相幅转换器,并且改进了传统的CORDIC算法,减少了部分角度存储,改善了传统方法的局限性。
