局部湿润模型模拟南疆滴灌枣园蒸散量及蒸腾量适用性研究*
2019-05-08赵经华马英杰
郑 明,赵经华, 马英杰, 洪 明
局部湿润模型模拟南疆滴灌枣园蒸散量及蒸腾量适用性研究*
郑 明,赵经华**, 马英杰, 洪 明
(新疆农业大学水利与土木工程学院 乌鲁木齐 830052)
为构建适用于模拟南疆滴灌成龄枣园蒸散及其组成成分的模型, 了解枣园土壤蒸发特征,本研究在双源模型和局部湿润灌溉方式下稀疏植被蒸散估算模型基础之上构建滴灌枣园局部湿润模型,以涡度相关法实测2017年枣园蒸散数据, 对双源模型(Shuttleworth-Wallace)及滴灌枣园局部湿润模型(Partial Root-zone Irrigation model)系数进行拟合; 之后通过评价两种模型模拟值的可靠性以及增加和减少模型参数10%来观测模型各参数对蒸散的影响方式, 并校验各模型参数计算公式的准确性; 然后以涡度相关法与液流法实测的2018年枣园蒸散与蒸腾量为基准值, 对双源模型与滴灌枣园局部湿润模型模拟2018年枣园蒸散及蒸腾量的可靠性进行评价, 筛选出适合模拟南疆滴灌枣园蒸散及其组分的模型并模拟滴灌枣园土壤蒸发特征。结果表明: 滴灌枣园局部湿润模型和双源模型的模型系数拟合准确; 依据模型模拟评价标准, 两种模型模拟2018年枣园蒸散的结果均为极好, 且精度基本一致。滴灌枣园局部湿润模型模拟蒸腾量结果良好, 与实际测定值之间的差值为15.73 mm; 双源模型模拟蒸腾量结果不可取。因此筛选出滴灌枣园局部湿润模型模拟枣园土壤蒸发, 枣园土壤蒸发量占蒸散量的19.74%。滴灌枣园局部湿润模型可以准确估算滴灌成龄枣园蒸散及蒸散组成成分。
枣园; 蒸散; 蒸腾; 局部湿润模型; 双源模型; 土壤蒸发
蒸散(evapotranspiration, ET)由植株蒸腾和土壤蒸发组成, 它既是地表能量平衡的重要成分, 又是水量平衡中重要的要素[1], 在能量转换和水循环中起着极其重要的作用, 且是连接生态与水文的重要纽带[2]。植物体通过根从土壤中吸收的水分, 只有约1%被植物体利用, 99%以上的水都通过蒸腾作用以水蒸气的形式从叶片的气孔散发到大气中[3]。因此准确估算农田ET及其组成成分对科学制定灌溉制度、提升作物水分生产力及合理利用有限的水资源有重大意义[4]。
涡度相关法(以下简称EC)作为测定ET最可靠方法之一[5-7], 在森林方面已有广泛应用[8], EC测定的ET常被用作其他方法估算ET精度的参考依据[9]。茎流法也被作为测定植株蒸腾量最可靠的方法[10]。由于仪器测定ET会受到诸多时空因素限制, 因此应用模型估算ET对于农业水管理是一种有效的途径[11]。在已开发的众多ET估算模型中, 应用相对广泛的是Shuttleworth-Wallace Model[12-13](双源模型, 以下简称SW模型)。SW模型在冠层较稀疏的生态系统适用性较强, 且能拆分ET。但SW模型假设土壤的含水率均一, 未考虑地表湿润程度和湿润面积对ET及ET组成成分的影响, 且在沟灌、滴灌、小管出流等局部湿润的农田应用研究报道较少[14]。Zhang等[15]使用SW模型对沟灌葡萄()园ET进行模拟, 模拟结果精度较高, 但并未分析SW模型模拟ET组成成分的精度。此后为准确估算沟灌葡萄园ET组成成分, 张宝忠等[16]提出局部湿润灌溉方式下稀疏植被蒸散估算模型(PRI-ET模型)原理及公式, 并成功构建沟灌葡萄园蒸散估算模型, 且模拟结果较好。但此模型理论在滴灌方式下枣园适用性有待验证。因此, 本研究在张宝忠构建PRI-ET模型和SW模型基础之上, 构建滴灌枣园局部湿润模型(PRI-ET模型)。滴灌枣园PRI-ET模型将土壤蒸发分为干燥土壤区蒸发与湿润土壤区蒸发, 将冠层蒸腾分为干燥土壤区上层冠层蒸腾量与湿润土壤区上方冠层蒸腾量。该模型精度还需验证, 故将滴灌枣园PRI-ET模型与已经应用广泛的SW模型分别模拟枣园ET及其组成成分, 并将模拟结果与涡度相关法及液流法实测值进行对比分析, 评价出更加适合模拟新疆南部果园ET及ET组成成分的模型。为筛选精确估算新疆南部地区果园特有种植模式及灌水方法下的ET模型, 为当地水资源合理分配提供可靠依据。
1 材料与方法
1.1 试验区概况及试验材料
试验于2017年和2018年在新疆阿克苏地区阿克苏市南工业园进行(80°36′E, 41°09′N)。试验田地势较为平坦, 平均海拔1 133 m。坡降为10‰~25‰, 地形较为平缓。
试验田面积为300 m×300 m。供试果树为15 a(2017年)生灰枣()树, 枣园为低矮密植成龄果园, 株行距为2 m×4 m, 平均株高4 m。灌水方式为滴灌, 滴灌带布置方式为1行3管, 滴头流量3.2 L·h–1, 滴头间距30 cm。滴灌带布设位置: 与树行垂直距离为1.3 m, 与树行方向平行, 树行两侧各布设1条; 滴灌管沿树行方向紧贴枣树布置。灌水周期为5 d, 灌水量根据上一灌水周期的枣园蒸散量减去降雨量确定, 若灌水周期内无降雨, 则灌水定额为上一灌水周期的枣园蒸散量。试验田土壤性质见表1。2017年与2018年枣园能量闭合度为0.79与0.80, 枣园能量闭合度符合文献报道范围[17], EC测定数据真实可靠。

表1 试验枣园土壤剖面基本物理性状
1.2 指标测定及仪器布设
1.2.1 ET观测
2017年4—10月与2018年4—9月枣园ET由Campbell公司生产的涡度相关系统(EC)进行测定(ETEC)。红外气体分析仪与三维超声风速仪(一体)(IRGASON, Campbell Scientific, USA)架设高度为6 m; 四分量辐射计(CNR-4)架设高度为5.5 m; 土壤热通量(HFP01SC)板共计两幅, 埋于地表以下8 cm处, 间距1 m; 土壤温度热电偶探头(TCAV)共计两幅, 一幅分为两个探针, 分别埋于地表以下2 cm和6 cm处, 两幅间距1 m。土壤热通量板与地表温度探针, 一幅埋于滴灌管下湿润土壤区, 另一幅埋于滴灌带与滴灌管之间干燥土壤区。土壤体积含水率由土壤三参数传感器测定, 传感器埋于株间滴灌管正下方地表以下2.5 cm处。以上传感器数据采集均由CR3000数据采集器(CR3000, Campbell Scientific, USA)采集, CR3000数据采集器原始采样频率为10 Hz, 设定记录时间为30 min。用CR3000内载Campbell Easy-Flux_DL在线全修正软件(Campbell Scientific Inc.2016)修正数据。
1.2.2 气象数据观测
试验地布设有小型自动监测气象站(Watchdog, USA)。气象站在枣树萌芽期前安装并设置启动运行, 架设高度为4.5 m, 气象站监测枣树全生育期内的太阳辐射、降雨量、风速、相对湿度、空气温度等气象因子, 记录时间设置为30 min。
1.2.3 叶面积指数观测
叶面积指数由HemiView数字植物冠层分析仪测定。HemiView分析仪器由有鱼眼广角镜头的单反数码相机和HemiView 2.1半球影像图片分析软件等组成。测定时间为8:30, 使用相机从东南西北4个方向拍摄3棵样树的冠层图片, 在枣树全生育期每隔10 d拍摄一次冠层图片。拍摄图片通过Photoshop软件预处理后, 使用HemiView 2.1软件进行分析, 计算出半球影像图片中所包含的冠层参数信息。
1.2.4 茎流数据观测
2018年枣园全生育期(5—9月)茎流数据采用热扩散探针法(TDP, Ecomatik, Germany)测定, 4月茎流仪出现故障, 故5月开始正常采集数据。传感器由两根探针组成, 一根加热探针, 另外一根为对照探针。通过给加热针加热来计算两根针的温度差, 最终计算树干茎流。一根探针安装在加热探针正下方且距地面60 cm的树干上, 上探针与下探针间距10 cm, 共选择3棵样树进行安装, 即3个重复。数据采集器(CR1000, Campbell Scientific, USA)自动监测和数据记录, 每2 min记录一次数据, 每10 min求其平均值, 使用间隔30 min的数据, 间隔10 min的数据用于校核间隔30 min的数据。
1.2.5 最小气孔阻力观测
在枣树各生育期内典型晴天, 将3棵样树分冠层顶层与底层两部分, 在样树冠层顶底两层的东南西北4个方向各选择1片树叶。10:00—20:00使用便携式光合测定系统CIRAS-3(PP SYSTEMS, USA)每间隔2 h测定样树选定叶片的光合数据, 每天共计测定6组数据, 1组数据共测定24片树叶。同一时间测定24片树叶气孔导度的平均值作为此时刻枣园气孔导度。最小气孔阻力是最大气孔导度的倒数。
1.3 模型介绍
1.3.1 SW模型
SW模型是在Penman-Monteith模型基础上, 引入了土壤阻力理论及地表空气动力学理论, 该模型将ET分为冠层蒸腾和土壤蒸发两部分, 从而更加全面地模拟作物蒸散过程。在作物冠层未完全发育时, 土壤蒸发量较大, PM模型不能很好地模拟作物实际ET及组成成分特征, 而SW模型由于理论优势则能很好地模拟作物ET特征, 因此SW模型适用性优于PM模型[18-19]。SW模型表达式[20]:
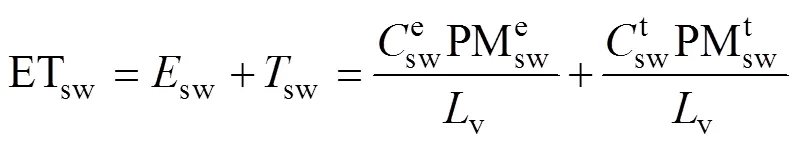

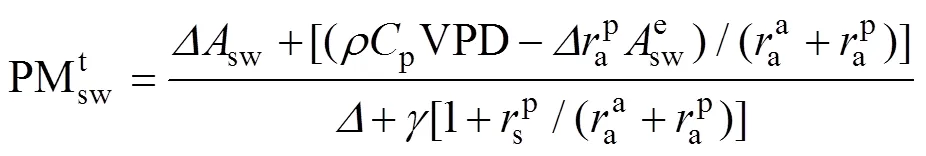
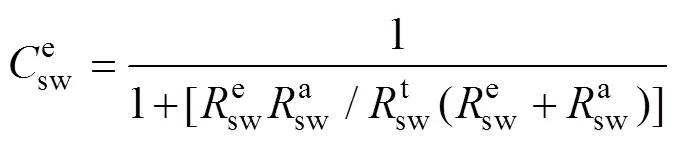
(5)



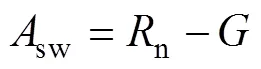
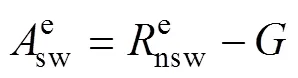
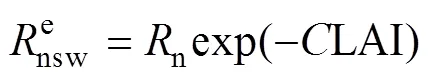

1.3.1.1 冠层阻力
该模型中的冠层阻力采用Jarvis的经验公式计算[22]:
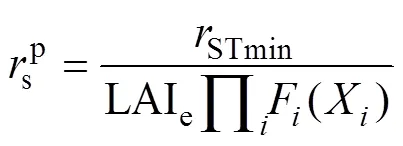

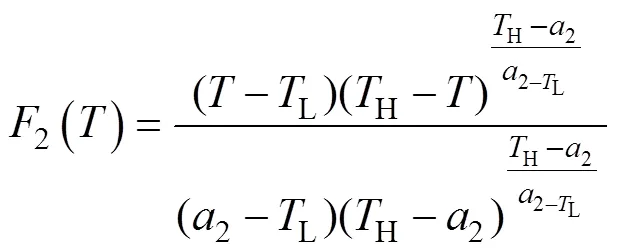
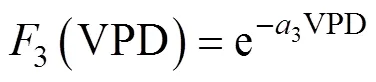
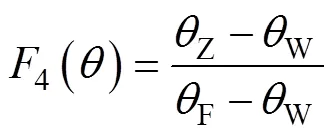
式中:为光合有效辐射(W∙m-2);为空气温度(℃);为土壤含水率(%);Z为根区土壤含水率(%);F为田间持水率(%);W为凋萎含水率(%), 当Z≥F,4()=1, 当Z≤F,4()=0, 当W≤Z≤F,4()取值按公式计算;H与L为作物停止生长的临界温度, 本文取值40 ℃和0 ℃[23]; e为常数, 取值为2.72;1、2和3为经验系数, 通过最小二乘法拟合获得。
1.3.1.2 空气动力学阻力
冠层上方的湍流扩散系数由下式表达[20]:

湍流扩散系数在冠层的表达式为[19]:

式中:h为冠层顶处的湍流扩散系数(m2·s–1);为湍流扩散系数, 作物高度c<1 m时,=2.5,c>10 m时,=4.25[24], 本文根据线性内插法取=3.08;为卡曼常数, 取值0.41;为参照高度(m);为零平面位移(m);*为参照高度处的摩擦风速(m∙s-1)。h的表达式为[25]:
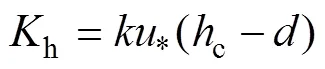

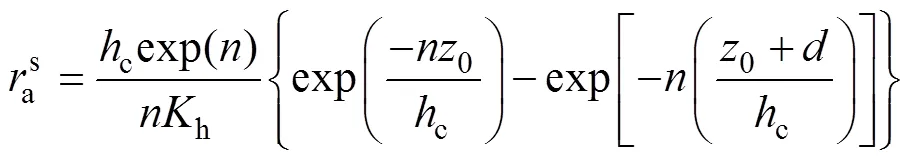
式中:0为动量传输粗糙度长度(m)。
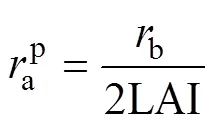
式中:b为单位冠层面积的边界层阻力, 表达式为[20]:
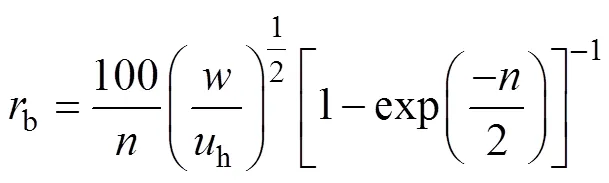
式中:h为冠上风速(m∙s-1);为典型叶片宽度, 本文取值6 cm[26]。
粗糙度长度0和零平面位移随作物高度c和叶面积指数LAI的改变而改变, 其表达式为[20]:

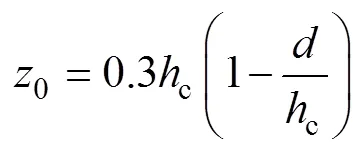

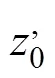
1.3.1.3 地表阻力
地表阻力表达式为[27]:
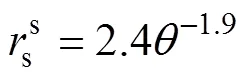
式中:为地表土壤含水率(%), 本文采用地表以下2.5 cm处的土壤含水率。
1.3.2 滴灌枣园PRI-ET模型
SW模型需要平均土壤含水率参数, 而滴灌、沟灌等局部湿润灌溉土壤的平均土壤含水率无法直接获得, 平均土壤含水率、干燥区土壤含水率与湿润区的土壤含水率面积加权平均值之间亦无相关性, 因此SW模型无法准确模拟局部湿润农田的土壤蒸发量。在SW模型和PRI-ET模型基础之上, 滴灌枣园PRI-ET模型将土壤蒸发分为干燥区土壤蒸发量与湿润区土壤蒸发量, 其计算更加准确。为使冠层与土壤划分标准匹配, 本研究将蒸腾分为土壤干燥区上方冠层蒸腾与土壤湿润区上方冠层蒸腾。因此滴灌枣园PRI-ET模型将ET分为土壤湿润区上方冠层蒸腾、土壤干燥区上方冠层蒸腾、湿润土壤蒸发及干燥土壤蒸发4部分。
滴灌枣园PRI-ET模型表达式如下[16]:
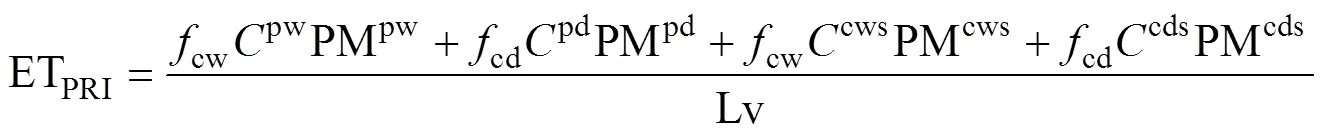
式中:cw为土壤湿润区面积与总面积比值, 实测计算为0.375;cd为土壤干燥区面积与总面积比值, 实测计算为0.625;pw、pd、cws与cds为相应比例系数, 无量纲; PMpw、PMpd、PMcws、PMcds分别表示土壤湿润区上方冠层蒸腾的潜热通量(MJ∙m-2∙d-1)、土壤干燥区上方冠层蒸腾的潜热通量(MJ∙m-2∙d-1)、土壤湿润区土壤蒸发潜热通量(MJ∙m-2∙d-1)、土壤湿润区土壤蒸发潜热通量(MJ∙m-2∙d-1), 以上4个物理量计算公式如下:
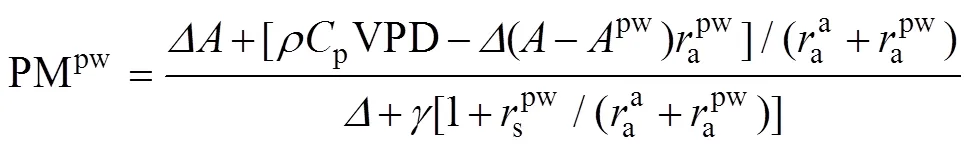
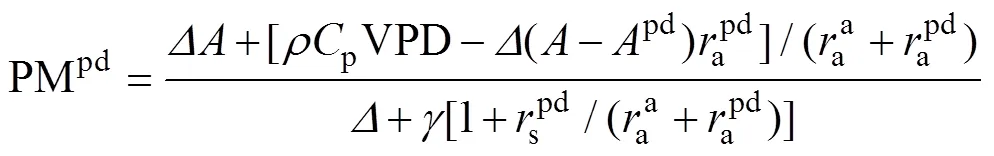
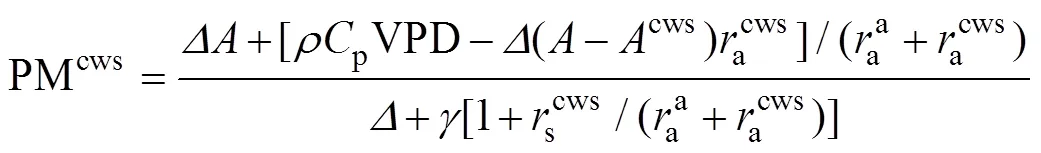

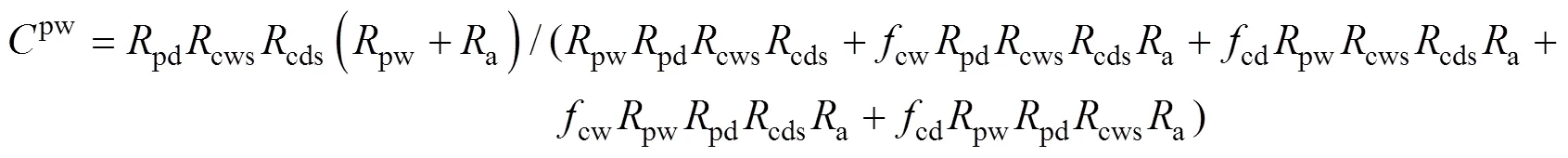



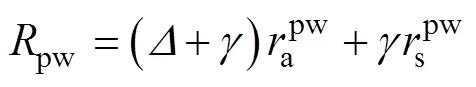

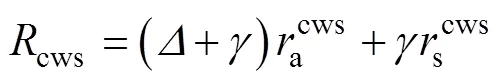


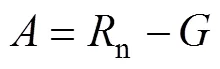
(43)


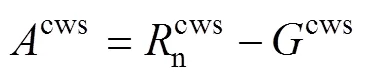

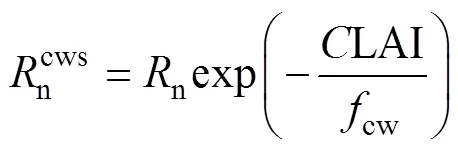
1.4 模型评价
根据前人研究[28-29]选取决定系数(coefficient of determination,2)、纳什系数(Nash Sutcliffe efficiency , NSE)和均方根误差与观测值标准差比率(RMSE-observations standard deviation ratio, RSR)评价模型模拟精度。0.75
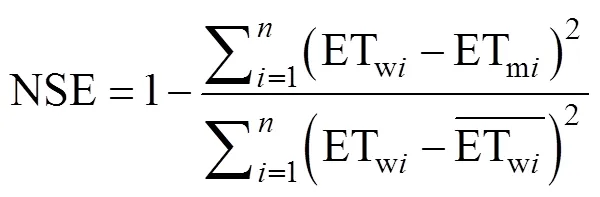
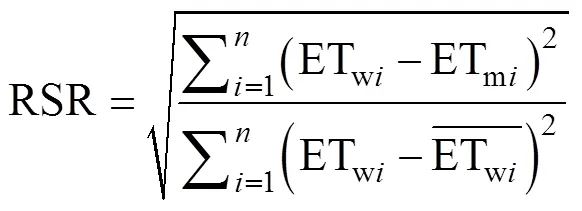
式中: ETwi为EC测定枣园第天ET, mm; ETmi为模型计算枣园的天ET, mm;为数据数量。
1.5 数据处理
采用Microsoft Excel 2010对数据进行统计及绘图, 使用Excel 2010和SPSS 20对模型模拟数据及仪器实测数据进行分析。
2 结果与分析
2.1 模型系数率定
以2017年EC实测枣园全生育期ET为基准值, 对SW模型与滴灌枣园PRI-ET模型进行系数拟合。由图1可知, 两种模型拟合系数后, 验证模型系数拟合精度, ETSW、ETPRI与ETEC变化特征和趋势基本一致, ETEC为551.06 mm, ETSW和ETPRI分别为562.58 mm、537.01 mm, ETSW、ETPRI与ETEC差值分别为11.52 mm和-14.05 mm, 差值分别占实测值的2.1%和-2.5%。ETSW、ETPRI与ETEC呈现极显著相关性(<0.01)。ETSW与ETEC之间的2为0.73, NSE为0.75, RSR为0.5。ETPRI与ETEC之间的2为0.87, NSE为0.81, RSR为0.44。说明两种模型均能较好地模拟枣园ET, 两模型系数拟合较准确。
2.2 模型敏感性分析
为保证模型可靠性, 需探究ET及其组分对参数的敏感性。本试验通过增加和减小10%的模型各阻力参数值, 观测2017年蒸散及其组分的变化量。由表2可知, 在滴灌枣园PRI-ET模型中, 对蒸腾影响最大的参数为LAI与sp, 蒸腾受aa影响较小, 其他阻力参数对蒸腾影响均为0。ap与sp对蒸发量影响为0, 其他参数对蒸发量影响较大, 其中scds与scws影响最大。对ET影响最大的是LAI与sp, 其他参数对其影响较小。在SW模型中, 对蒸腾影响最大的参数为LAI与sp, 蒸腾受其他参数影响较小。对ET影响最大的是LAI与sp, 其他参数对其影响较小。
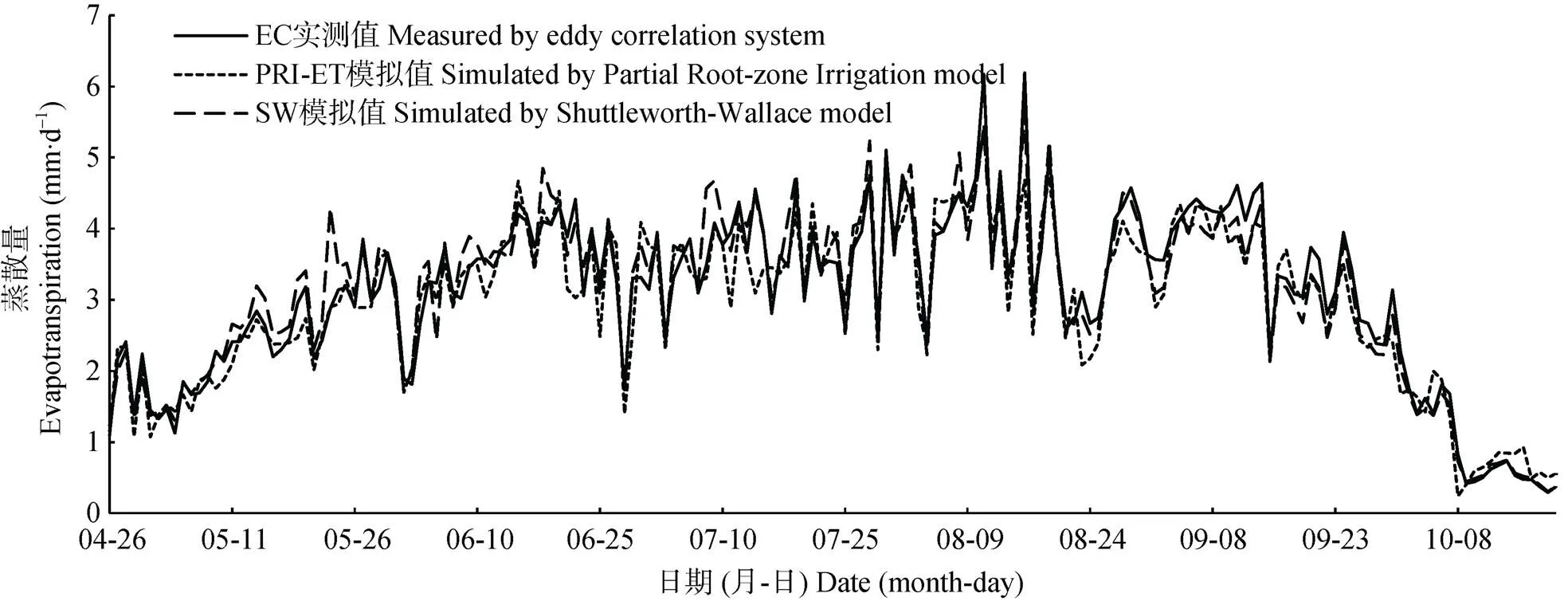
图1 SW模型、滴灌枣园PRI-ET模型和EC计算2017年滴灌枣园蒸散量对比
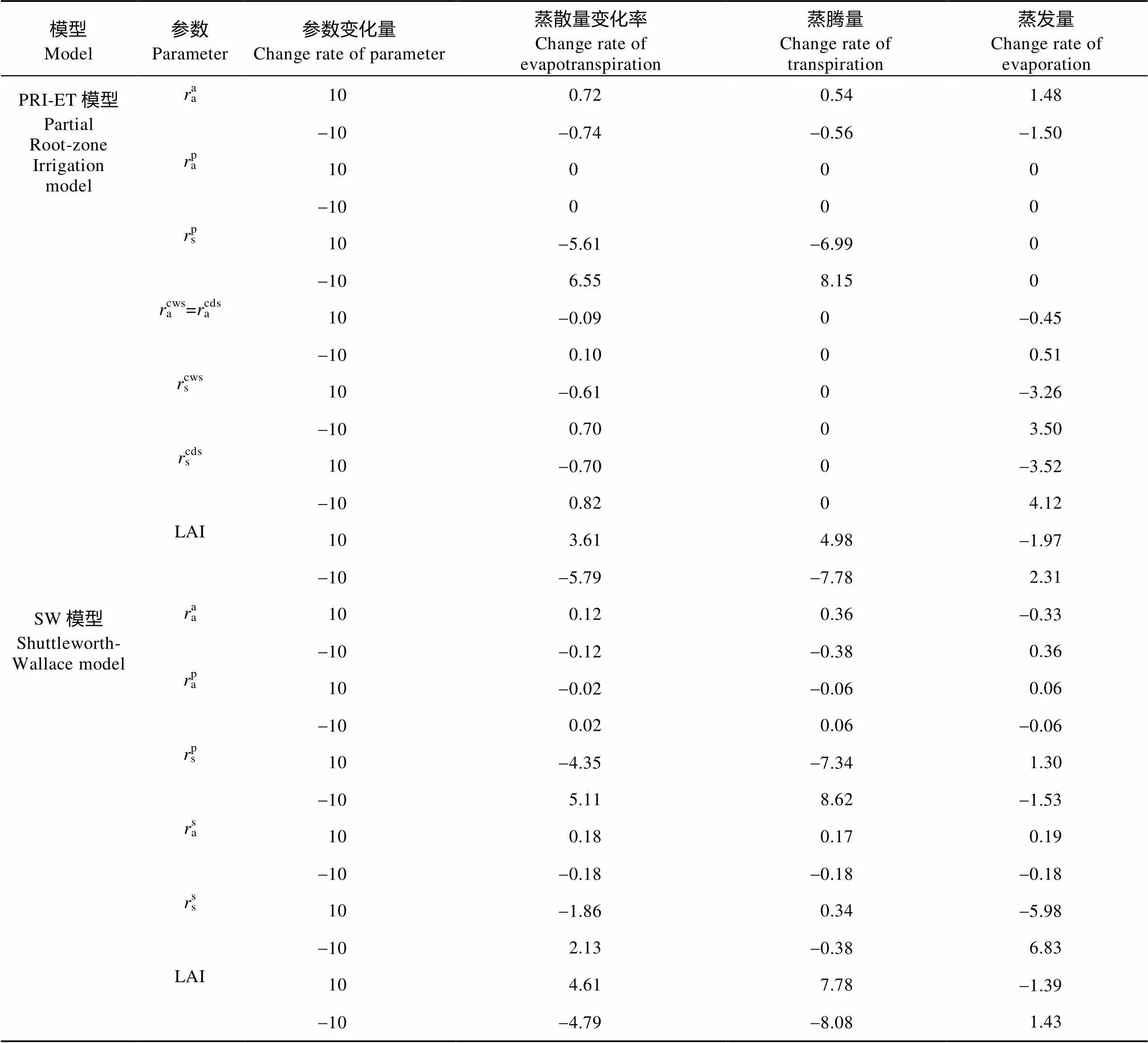
表2 滴灌枣园PRI-ET模型和SW模型模拟ET及其组分对参数变化±10%的敏感性
2.3 模型评价
2.3.1 2018年枣园实测ET与模型模拟ET的对比分析


图2 2018年枣园ET日实测值与两种模型模拟值
对2018年ETPRI、ETSW和ETEC进行线性回归分析, 由图3可知ETPRI()与ETEC()之间的线性回归方程为:=1.006 8,2为0.87, NSE为0.88, RSR为0.35。根据数据评价标准判断, 滴灌枣园PRI-ET模型模拟枣园ET结果为极好。ETSW()与ETEC()之间的线性回归方程为:=1.000 9,2为0.75, NSE为0.76, RSR为0.49。根据数据评价标准判断, SW模型模拟枣园ET结果也为极好。ETPRI相比ETSW,2的值与数据评价结果相对较高, 因此滴灌枣园PRI-ET模型相比SW模型在模拟枣园ET方面优势较突出。
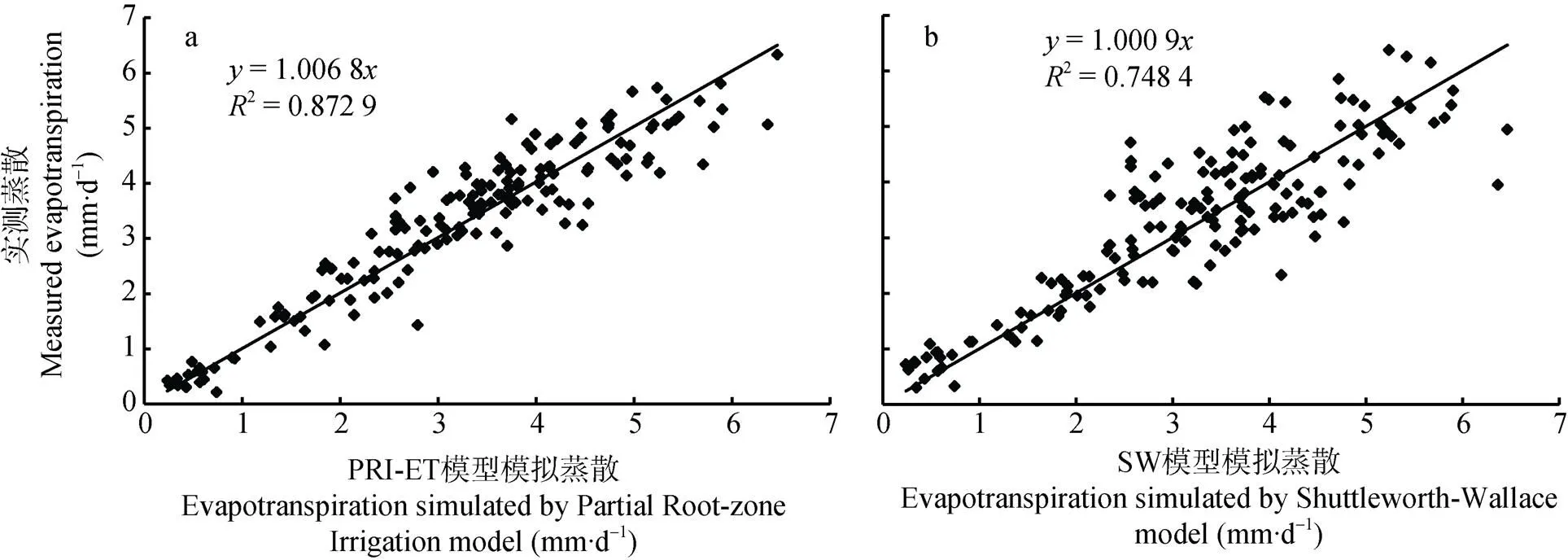
图3 2018年枣园ET日实测值与滴灌枣园PRI-ET(a)和SW模型(b)模拟值的线性回归分析
2.3.2 枣园实测蒸腾量与模型模拟蒸腾量的对比分析
4月份茎流仪出现故障, 因此枣园蒸腾量监测时间为5月6日—9月22日。使用滴灌枣园PRI-ET模型与SW模型对2018年枣园蒸腾量进行模拟。由图4可知, SW模型模拟蒸腾量(TSW)与茎流实测蒸腾量(JL)呈现明显不一致现象, 两种方法测定蒸腾量总差值为97.05 mm, 日均差值为0.70 mm·d–1。这是因为SW模型中的土壤含水率参数采用湿润区的土壤含水率, 而湿润区的土壤含水率相比整个枣园平均土壤含水率较高, 导致模型过高估算土壤蒸发量, 而EC实测ETEC不变, 因此在模型拟合系数时, 模型会相应低估蒸腾量。滴灌枣园PRI-ET模型模拟蒸腾量(PRI)与TJL变化特征及数值基本一致, 两种方法测定值之间的差值为15.73 mm, 日均差值为0.11 mm·d–1。说明滴灌枣园PRI-ET模型估算枣园的蒸腾量具有较高精度。由于滴灌枣园PRI-ET模型模拟土壤蒸发时考虑土壤干燥区土壤含水率、土壤湿润区土壤含水率、干燥土壤区的面积比及湿润土壤区的面积比等影响因素, 因此滴灌枣园PRI-ET模型模拟过程更符合枣园实际蒸散情况及特征, 因此能较准确地模拟枣园土壤蒸发量。
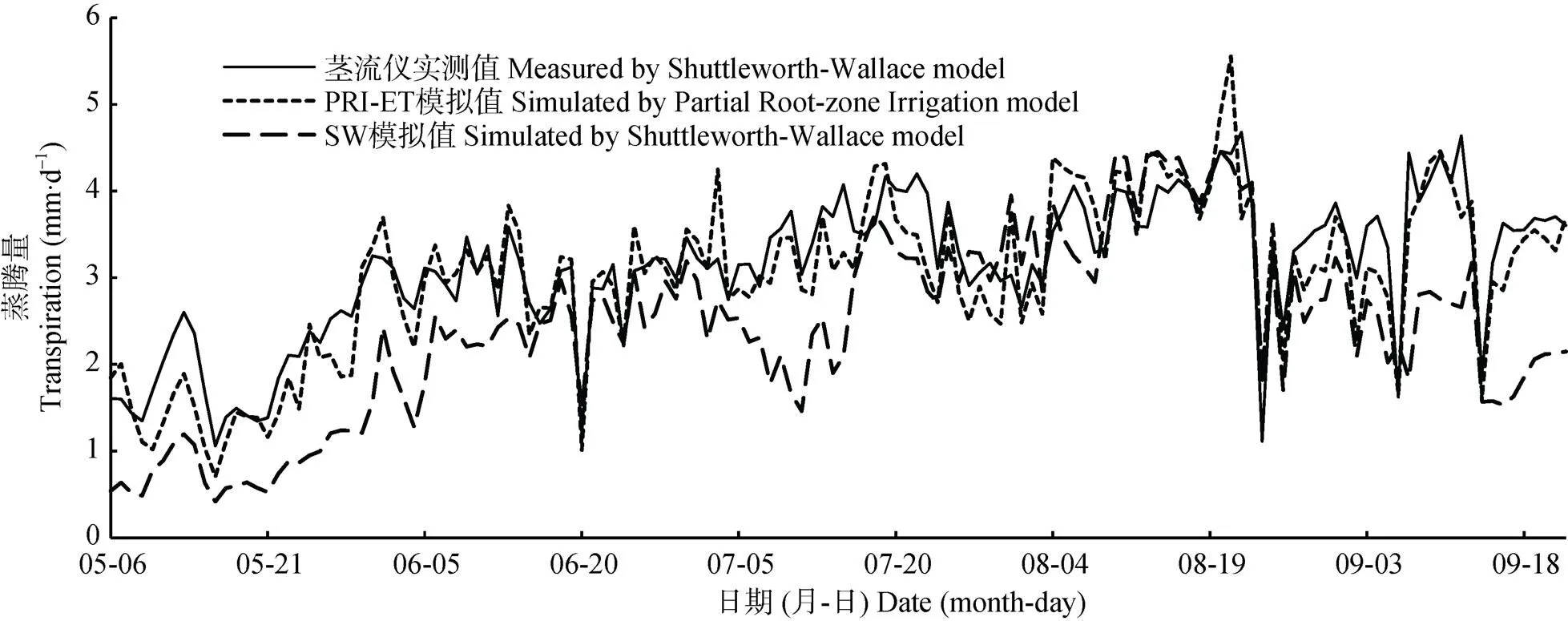
图4 2018年枣园蒸腾量日实测值与两种模型模拟值
对PRI、SW与JL进行线性回归分析, 如图5所示。PRI()与JL()之间的线性回归方程为:=1.015 5,2为0.74, NSE为0.73, RSR为0.52。由数据评价标准判断, 滴灌枣园PRI-ET模型模拟结果为良好。SW()与JL()之间的线性回归方程为:=0.586 11.697 1,2为0.55, NSE为-0.44, RSR为1.20。由数据评价标准判断, SW模型模拟结果不可取。
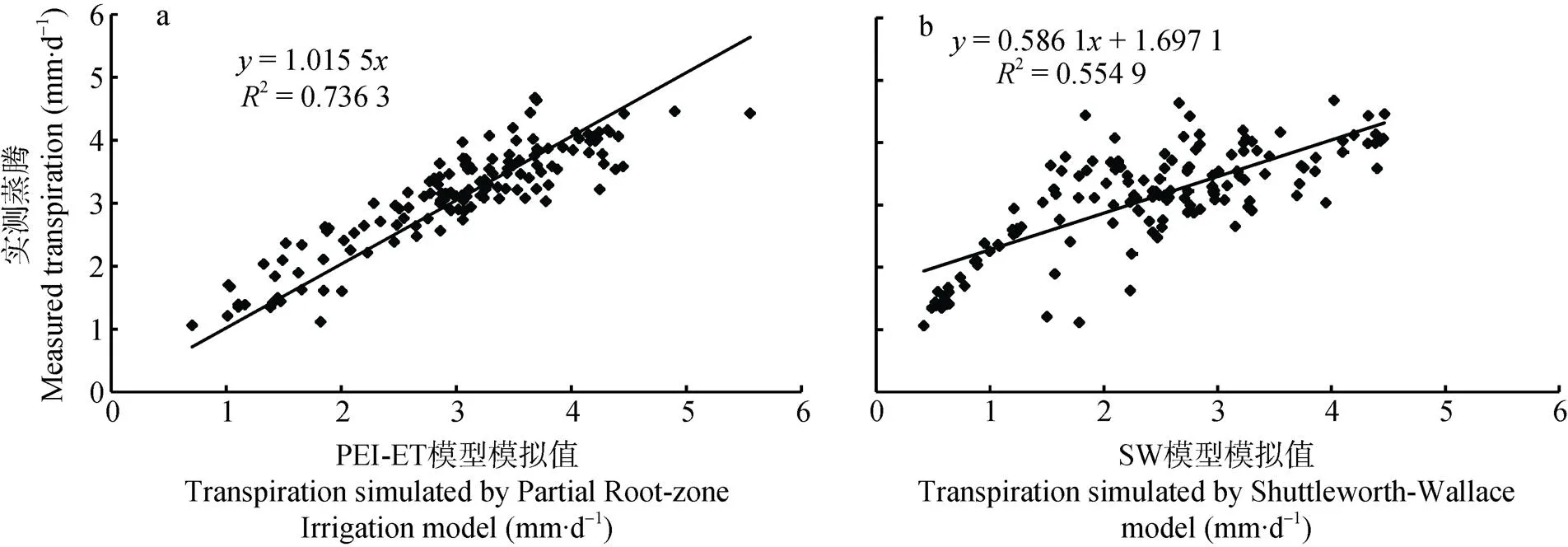
图5 2018年枣园蒸腾量日实测值与滴灌枣园PRI-ET(a)和SW模型(b)模拟值线性回归分析
2.4 枣园土壤蒸发特征
使用滴灌枣园PRI-ET模型估算2018年枣园内日土壤蒸发强度如图6所示。枣园日土壤蒸发强度呈现先增大后减小的变化趋势, 监测期内枣园总土壤蒸发量为106.52 mm, 占总蒸散量19.74%。4月12日至6月25日枣园内日土壤蒸发强度较小, 但此时的日土壤蒸发比(日土壤蒸发量/当天的蒸散量)较大。此阶段灌水量较小、灌水时间较短、气温与太阳辐射等气象因子相对较低, 以上因素使得日土壤蒸发强度较小, 而此时枣园蒸腾量较小, 因此日土壤蒸发比相对较大。6月26日至8月31日, 此阶段是枣树果实发育期, 此发育期耗水量最大, 叶面积指数也达到最大, 是枣园需水关键期。因此为保证枣树正常需水要求, 该时期枣园灌水时间比其他时间长, 造成湿润区的土壤含水率相比其他时间段高; 此外在这一时段气温与太阳辐射气象因子均达到最大, 使得土壤蒸发量加大, 因此该阶段枣园日土壤蒸发强度最大, 但此时的日土壤蒸发比相对较小, 枣园蒸腾量较大, 使得日土壤蒸发强度占比较小。8月31日至9月22日的日土壤蒸发强度较小, 此时的灌水量较小、气温与太阳辐射下降使得日土壤蒸发强度与日土壤蒸发占比较小。总体来说, 滴灌条件下矮化密植模式的农田相比其他灌溉方式及种植模式农田可以有效减小作物无效耗水量(土壤蒸发)。

图6 滴灌枣园PRI-ET模型估算的枣园日土壤蒸发强度及日土壤蒸发比变化特征
3 讨论
本研究通过对参数增加与减小±10%, 发现对ET影响最大的是LAI与sp, 与前人[30-32]研究结论一致。使用SW模型与滴灌枣园PRI-ET模型对2018年ET与蒸腾量进行模拟, 滴灌枣园PRI-ET模型相比SW模型具有较高精度。使用两种模型模拟枣园蒸腾量时, 发现滴灌枣园PRI-ET模型模拟结果与实测结果变化特征基本一致, 而SW模型模拟结果与实测结果呈现较大差异, 滴灌枣园PRI-ET模型在模拟枣园蒸腾量方面的精度远高于SW模型。这是因为SW模型模拟土壤蒸发时, 使用的是滴灌带下湿润区土壤含水率, 而湿润区面积仅占总面积的0.375, 因此SW模型会高估土壤蒸发量, 即高估ET。但SW模型是以实测ET为基础拟合参数, 无形中增加了冠层阻力的值, 即低估植株蒸腾量来弥补高估土壤蒸发的部分。因此SW模型相比滴灌枣园PRI-ET模型在计算蒸散量的精度虽相近, 但若要分别分析枣园ET组成成分时, SW模型精度远低于滴灌枣园PRI-ET模型。
本研究还发现, 利用滴灌枣园PRI-ET模型对枣园ET及枣树蒸腾量进行估算, 其精度相比卫新东等[14]使用SW模型模拟陕北枣林ET较低。这是因为枣树每个生育期都有其各自特点[26], 本研究以全生育期为基准, 对模型进行率定系数, 这可能会对计算ET产生较大误差; 此外本试验由于缺乏对干燥区土壤含水率连续的监测, 而假设干燥区土壤含水率短时间内不变, 采用烘干法定期对干燥土壤含水率进行测定, 会存在较大误差。
研究还发现本试验区土壤蒸发量远远小于艾鹏睿等[33]的研究结果, 艾鹏睿研究结果为土壤蒸发占ET的40%, 而本试验土壤蒸发仅占ET的19.74%。这可能是种植模式及土壤性质不同所致, 其中种植模式影响叶面积指数, 而叶面积指数是影响土壤蒸发的重要因素[34]。本试验田为低矮密植成龄枣树, 叶面积指数较大。而艾鹏睿等的试验对象为幼龄枣树且种植行间距为成龄枣树的标准, 因此其枣树叶面积指数较小。此外两试验田虽相距不远, 但土壤性质却完全不同, 本试验田为细砂, 相比艾鹏睿等试验的壤土, 灌溉水迅速下渗且在同等灌水条件下地表湿润面积较小, 留存于地表湿润区水分较少, 故土壤蒸发量较少。这也侧面说明滴灌条件下, 细砂土壤相比壤土可以有效减少农田无效耗水, 达到有效节水目的。
本研究虽根据当地种植模式及滴灌条件构建滴灌枣园PRI-ET模型, 但模型精度仍未达到理想状态, 这是由于数据采集有所欠缺及未针对各生育期调整系数所致, 为提高滴灌枣园PRI-ET模型精度, 仍需后续工作深入研究。
4 结论
对滴灌枣园局部湿润模型与双源模型的系数进行拟合, 拟合系数后两模型均可以较好地模拟枣园蒸散量, 且两种模型精度基本一致。但在模拟枣园蒸散量组成成分方面, 滴灌枣园局部湿润模型可以较好地模拟枣园蒸散量组成成分, 而双源模型模拟结果不可取, 因此建议使用滴灌枣园局部湿润模型模拟枣园蒸散组成成分。应用滴灌枣园局部湿润模型模拟2018年枣园土壤蒸发为106.52 mm, 仅占蒸散量的19.74%, 远低于其他相关研究, 说明土壤性质对土壤蒸发量影响较大。
[1] XU C Y, SINGH V P. Evaluation of three complementary relationship evapotranspiration models by water balance approach to estimate actual regional evapotranspiration in different climatic regions[J]. Journal of Hydrology, 2005, 308(1/4): 105–121
[2] 张宝忠, 许迪, 刘钰, 等. 多尺度蒸散发估测与时空尺度拓展方法研究进展[J]. 农业工程学报, 2015, 31(6): 8–16 ZHANG B Z, XU D, LIU Y, et al. Review of multi-scale evapotranspiration estimation and spatio-temporal scale expansion[J]. Transactions of the CSAE, 2015, 31(6): 8–16
[3] RANA G, KATERJI N. Measurement and estimation of actual evapotranspiration in the field under Mediterranean climate: A review[J]. European Journal of Agronomy, 2000, 13(2/3): 125–153
[4] 石小虎, 蔡焕杰, 赵丽丽, 等. 基于SIMDualKc模型估算非充分灌水条件下温室番茄蒸发蒸腾量[J]. 农业工程学报, 2015, 31(22): 131–138 SHI X H, CAI H J, ZHAO L L, et al. Estimation of greenhouse tomato evapotranspiration under deficit irrigation based on SIMDualKc model[J]. Transactions of the CSAE, 2015, 31(22): 131–138
[5] 刘海军, 黄冠华, TANNY J, 等. 用涡度相关法测定网室内香蕉树蒸散量[J]. 农业工程学报, 2008, 24(9): 1–5 LIU H J, HUANG G H, TANNY J, et al. Measurement of banana tree evapotranspiration in screen house using eddy covariance method[J]. Transactions of the CSAE, 2008, 24(9): 1–5
[6] Massman W J, Lee X. Eddy covariance flux corrections and uncertainties in long-term studies of carbon and energy exchanges[J]. Agricultural & Forest Meteorology, 2002, 113(1): 121-144
[7] 王维真, 徐自为, 刘绍民, 等. 黑河流域不同下垫面水热通量特征分析[J]. 地球科学进展, 2009, 24(07): 714-723 WANG W Z, XU Z W, LIU S M, et al. The characteristics of heat and water vapor fluxes over different surfaces in the Heihe River Basin[J]. Advances in Earth Science, 2009, 24(7): 714-723
[8] 黄辉, 孟平, 张劲松, 等. 华北低丘山地人工林蒸散的控制因子[J]. 生态学报, 2014, 34(3): 667–673 HUANG H, MENG P, ZHANG J S, et al. Stomatal and environmental control on evapotranspiration in a plantation in the lower mountain areas of North China[J]. Aca Ecologica Sinica, 2014, 34(3): 667–673
[9] 杨凡, 齐永青, 张玉翠, 等. 大孔径闪烁仪与涡度相关系统对灌溉农田蒸散量的对比观测[J]. 中国生态农业学报, 2011, 19(5): 1067–1071 YANG F, QI Y Q, ZHANG Y C, et al. Comparative advantages of large aperture Scintiilometer and Eddy Covariance instrument for measuring evapotranspiration in irrigated farmlands[J]. Chinese Journal of Eco-Agriculture, 2011, 19(5): 1067–1071
[10] 屈艳萍, 康绍忠, 王素芬, 等. 液流—株间微型蒸渗仪法测定新疆杨蒸发蒸腾量适用性分析[J]. 干旱地区农业研究, 2014, 32(3): 88–94 QU Y P, KANG S Z, WANG S F, et al. Applicability analysis for measuring evapotranspiration ofvar. by sap flow and micro-lysimeter method[J]. Agricultural Research in the Arid Areas, 2014, 32(3): 88–94
[11] VILLARREAL-GUERRERO F, KACIRA M, FITZ-RODRÍGUEZ E, et al. Comparison of three evapotranspiration models for a greenhouse cooling strategy with natural ventilation and variable high pressure fogging[J]. Scientia Horticulturae, 2012, 134: 210–221
[12] 朱仲元, 朝伦巴根, 王志强, 等. 基于Shuttleworth-Wallace双源模型的天然杨树蒸散量日变化研究[J]. 水利学报, 2007, 38(5): 582–590 ZHU Z Y, CHAO L B G, WANG Z Q, et al. Study on diurnal variation ofevapotranspiration based on Shuttleworth-Wallace model[J]. Journal of Hydraulic Engineering, 2007, 38(5): 582–590
[13] 杨雨亭, 尚松浩. 双源蒸散发模型估算潜在蒸散发量的对比[J]. 农业工程学报, 2012, 28(24): 85–91 YANG Y T, SHANG S H. Comparison of dual-source evapotranspiration models in estimating potential evaporation and transpiration[J]. Transactions of the CSAE, 2012, 28(24): 85–91
[14] 卫新东, 刘守阳, 陈滇豫, 等. Shuttleworth-Wallace模型模拟陕北枣林蒸散适用性分析[J]. 农业机械学报, 2015, 46(3): 142–151 WEI X D, LIU S Y, CHEN D Y, et al. Applicability of Shuttleworth-Wallace model for evapotranspiration estimation of jujube forests in loess hilly-gully region[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(3): 142–151
[15] ZHANG B Z, KANG S Z, LI F S, et al. Comparison of three evapotranspiration models to Bowen ratio-energy balance method for a vineyard in an arid desert region of northwest China[J]. Agricultural and Forest Meteorology, 2008, 148(10): 1629–1640
[16] 张宝忠, 康绍忠, 刘钰. 局部湿润灌溉方式下稀疏植被蒸散估算模型——以沟灌葡萄园为例[C]//现代节水高效农业与生态灌区建设. 北京: 中国农业工程学会, 2010: 11 ZHANG B Z, KANG S Z, LIU Y. Estimation model for evapotranspiration of sparse vegetation under partial wetting irrigation: A case study of vineyard in furrow irrigation[C]//Proceedings of the Modern Water-Saving and Efficient Agriculture and Ecological Irrigation Area Construction. Beijing: Chinese Society of Agricultural Engineering, 2010: 11
[17] WILSON K, GOLDSTEIN A, FALGE E, et al. Energy balance closure at FLUXNET sites[J]. Agricultural and Forest Meteorology, 2002, 113(1/4): 223–243
[18] BRISSON N, ITIER B, L’HOTEL J C, et al. Parameterisation of the Shuttleworth-Wallace model to estimate daily maximum transpiration for use in crop models[J]. Ecological Modelling, 1998, 107(2/3): 159–169
[19] 母艳梅, 李俊, 同小娟, 等. 基于Penman-Monteith模型和Shuttleworth-Wallace模型对太行山南麓人工林蒸散的模拟[J]. 北京林业大学学报, 2017, 39(11): 35–44 MU Y M, LI J, TONG X J, et al. Evapotranspiration simulated by Penman-Monteith and Shuttleworth-Wallace models over a mixed plantation in the southern foot of the Taihang Mountain, northern China[J]. Journal of Beijing Forestry University, 2017, 39(11): 35–44
[20] SHUTTLEWORTH W J, WALLACE J S. Evaporation from sparse crops —an energy combination theory[J]. Quarterly Journal of the Royal Meteorological Society, 1985, 111(469): 839–855
[21] ZHOU M C, ISHIDAIRA H, HAPUARACHCHI H P, et al. Estimating potential evapotranspiration using Shuttleworth-Wallace model and NOAA-AVHRR NDVI data to feed a distributed hydrological model over the Mekong River basin[J]. Journal of Hydrology, 2006, 327(1/2): 151–173
[22] JARVIS P G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field[J]. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 1976, 273(927): 593–610
[23] HARRIS P P, HUNTINGFORD C, COX P M, et al. Effect of soil moisture on canopy conductance of Amazonian rainforest[J]. Agricultural and Forest Meteorology, 2004, 122(3/4): 215–227
[24] BRUTSAERT W. Evaporation into the Atmosphere: Theory, History and Applications[M]. Netherlands: Springer, 1982
[25] KATO T, KIMURA R, KAMICHIKA M. Estimation of evapotranspiration, transpiration ratio and water-use efficiency from a sparse canopy using a compartment model[J]. Agricultural Water Management, 2004, 65(3): 173–191
[26] 刘守阳. 黄土丘陵沟壑区旱作山地枣林耗水规律研究[D]. 杨凌: 西北农林科技大学, 2013: 39–49LIU S Y. Law of rainfed jujube forest evapotranspiration in the loess hill and gully area[D]. Yangling: Northwest A&F University, 2013: 39–49
[27] 高冠龙, 张小由, 鱼腾飞, 等. Shuttleworth-Wallace双源蒸散发模型阻力参数的确定[J]. 冰川冻土, 2016, 38(1): 170–177 GAO G L, ZHANG X Y, YU T F, et al. Calculation methods of resistances of the Shuttleworth-Wallace model[J]. Journal of Glaciology and Geocryology, 2016, 38(1): 170–177
[28] ROSA R D, PAREDES P, RODRIGUES G C, et al. Implementing the dual crop coefficient approach in interactive software: 2. Model testing[J]. Agricultural Water Management, 2012, 103: 62–77
[29] 王子申, 蔡焕杰, 虞连玉, 等. 基于SIMDualKc模型估算西北旱区冬小麦蒸散量及土壤蒸发量[J]. 农业工程学报, 2016, 32(5): 126–136WANG Z S, CAI H J, YU L Y, et al. Estimation of evapotranspiration and soil evaporation of winter wheat in arid region of Northwest China based on SIMDualKc model[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(5): 126–136
[30] LI X Y, YANG P L, REN S M, et al. Modeling cherry orchard evapotranspiration based on an improved dual-source model[J]. Agricultural Water Management, 2010, 98(1): 12–18
[31] 吴林, 闵雷雷, 沈彦俊, 等. 分时段修正双源模型在西北干旱区玉米蒸散量模拟中的应用[J]. 中国生态农业学报, 2017, 25(5): 634–646WU L, MIN L L, SHEN Y J, et al. Simulation of maize evapotranspiration at different growth stages using revised dual-layered model in arid Northwest China[J]. Chinese Journal of Eco-Agriculture, 2017, 25(5): 634–646
[32] 李俊, 韩凤明, 同小娟, 等. 麦田蒸散模型的改进及其对阻力参数的敏感性分析[J]. 中国农业气象, 2014, 35(6): 635–643LI J, HAN F M, TONG X J, et al. Evapotranspiration models for a winter wheat field: The improvements and analyses on their sensitivities to the resistance parameters[J]. Chinese Journal of Agrometeorology, 2014, 35(6): 635–643
[33] 艾鹏睿, 马英杰, 马亮. 干旱区滴灌枣棉间作模式下枣树棵间蒸发的变化规律[J]. 生态学报, 2018, 38(13): 4761–4769AI P R, MA Y J, MA L. Study on evaporation variation of jujube trees under drip irrigation of jujube and cotton intercropping in an arid area[J]. Acta Ecologica Sinica, 2018, 38(13): 4761–4769
[34] 王新, 刘洪波, 张江辉, 等. 不同水分条件下干旱区葡萄园土面蒸发试验研究[J]. 土壤学报, 2012, 49(5): 1050–1055WANG X, LIU H B, ZHANG J H, et al. Experimental study on soil evaporation in vineyards different in soil moisture in arid region[J]. Acta Pedologica Sinica, 2012, 49(5): 1050–1055
Applicability of Partial Root-zone Irrigation model to simulate evapotranspiration and transpiration in drip irrigation jujube orchards in southern Xinjiang*
ZHENG Ming, ZHAO Jinghua**, MA Yingjie, HONG Ming
(College of Hydraulic and Civil Engineering, Xinjiang Agricultural University, Urumqi 830052, China)
Constructing a model suitable for simulating evapotranspiration and evapotranspiration components of mature jujube orchard under drip irrigation in southern Xinjiang and understanding their soil evaporation characteristics would be beneficial for growers. Based on the Shuttleworth-Wallace model and the evapotranspiration estimation model of sparse vegetation under local wet irrigation, a Partial Root-zone Irrigation model of drip irrigation for the jujube orchard was constructed. The evapotranspiration data were measured by eddy correlation methods in the jujube orchard in 2017, and the coefficients of the Shuttleworth-Wallace model and the Partial Root-zone Irrigation model of drip irrigation for jujube orchard were fitted and evaluated; the effects of the model parameters on evapotranspiration were observed by increasing and decreasing the model parameters by 10%, and the accuracy of the formulas for calculating the parameters of each model was verified. Evapotranspiration was then measured using the eddy correlation method and transpiration was measured using the liquid flow method to obtain accurate values. The reliability of the two models used to simulate evapotranspiration and transpiration in jujube orchard in 2018 were evaluated. The models were suitable for calculating evapotranspiration and evapotranspiration components in the drip irrigation jujube orchard of southern Xinjiang in 2018, as well as simulating the soil evaporation characteristics. Model coefficients of the Shuttleworth-Wallace model and Partial Root-zone Irrigation model for the drip irrigation jujube orchard were accurately fitted according to the criteria for evaluating the simulation results of the model. The results of the two models for simulating evapotranspiration were excellent for the jujube orchard in 2018, and the accuracy of the two models were the same. The results of the Partial Root-zone Irrigation model for drip irrigation jujube orchard were also good, with a difference of 15.73 mm between the model and actual measured value. It was not advisable to simulate transpiration by using the Shuttleworth-Wallace model. Therefore, the Partial Root-zone Irrigation model for drip irrigation was selected to simulate soil evaporation in the jujube orchard, and the results showed that soil evaporation accounted for 19.74% of the evapotranspiration. Thus, the Partial Root-zone Irrigation model for the drip irrigation jujube orchards can be used to accurately estimate the evapotranspiration and evapotranspiration components of the orchards.
Jujube orchard; Evapotranspiration; Transpiration; Partial Root-zone Irrigation model; Shuttleworth-Wallace model; Soil evaporation
, E-mail: zhaojinghua__xj@126.com
Nov. 8, 2018;
Dec. 26, 2018
S715.4
A
2096-6237(2019)05-0726-12
10.13930/j.cnki.cjea.180984
郑明, 赵经华, 马英杰, 洪明. 局部湿润模型模拟南疆滴灌枣园蒸散量及蒸腾量适用性研究[J]. 中国生态农业学报(中英文), 2019, 27(5): 726-737
ZHENG M, ZHAO J H, MA Y J, HONG M. Applicability of Partial Root-zone Irrigation model to simulate evapotranspiration and transpiration in drip irrigation jujube orchards in southern Xinjiang[J]. Chinese Journal of Eco-Agriculture, 2019, 27(5): 726-737
* 新疆教育厅创新项目(XJEDU2017T004)和中国农业大学-新疆农业大学联合基金项目(2015TC051)资助
赵经华, 主要从事节水灌溉技术研究及教学工作。E-mail: zhaojinghua__xj@126.com
郑明, 主要从事节水灌溉技术研究。E-mail: xjzhengming@126.com
2018-11-08
2018-12-26
* This study was supported by the Innovation Project of Xinjiang Education Department (XJEDU2017T004) and China Agricultural University-Xinjiang Agricultural University Joint Fund Project (2015TC051).
