基于电力系统仿真软件的静止无功系统模型应用

杨健，徐政，游广增

(1.浙江大学电气工程学院，杭州 310027；2.云南电网有限责任公司电网规划建设研究中心，昆明 650011)

0 前言

静止无功系统（SVS）是静止无功补偿装置和机械投切的无功补偿装置的组合，各无功补偿装置的输出通过自动控制装置协调配合[1]。SVS能够快速调节注入系统的无功电流[2]，可以用于快速电压控制，同时还能起到提高系统电压稳定性、改善系统阻尼、抑制次同步振荡、改善配电网电能质量等作用[3-5]。如今，静止无功系统已经在世界范围内得到了广泛应用[6-7]。通过电力系统仿真软件对含SVS的电力系统进行研究是对SVS进行规划设计和考察安装SVS后电力系统特性的有效手段。要实现上述目标，首先需要建立SVS的仿真模型。

对SVS建模方面的研究已经比较成熟，美国西部电力协调委员会（the Western Electricity Coordinating Council，WECC）于2012年提出的SVS模型（svsmo1，svsmo2，svsmo3）在潮流计算和时域稳定性仿真中具有广泛的通用性。同时，模型的准确性也已经得到了多次验证[8]。研究表明，上述模型非常适用于电力系统仿真，能够可靠地模拟静止无功系统的动态特性[9]。目前，上述SVS模型已经在包括PSS/E在内的多个商业仿真程序中得到了应用。

PSS/E是美国电力技术公司（Power Technologies Inc，PTI）开发的电力系统仿真软件。它采用了先进的计算机技术和数值计算方法，功能强大，操作灵活，在国际上使用广泛。在国内已有的文献中，已经对PSS/E中直流系统模型、多端直流系统模型、柔性直流系统模型、SVC模型等进行了详细的介绍[10-13]，但对SVS模型的研究还比较少。

本文将讨论SVS模型在电力系统机电暂态计算程序中的模拟原则，分析基于PSS/E的SVS潮流和动态模型，并通过算例验证SVS的功能，比较SVS模型中慢速电纳控制、非线性斜率控制和直接死区控制的特点，为实际应用提供参考。

1 SVS的工作原理及模拟原则

1.1 SVS的工作原理

一种典型的SVS方案如图1所示，它由一个晶闸管控制电抗器（Thyristor Controlled Reactor，TCR）、一个三单元晶闸管投切电容器（Thyristor Switched Capacitor，TSC）和一个滤波器组成。

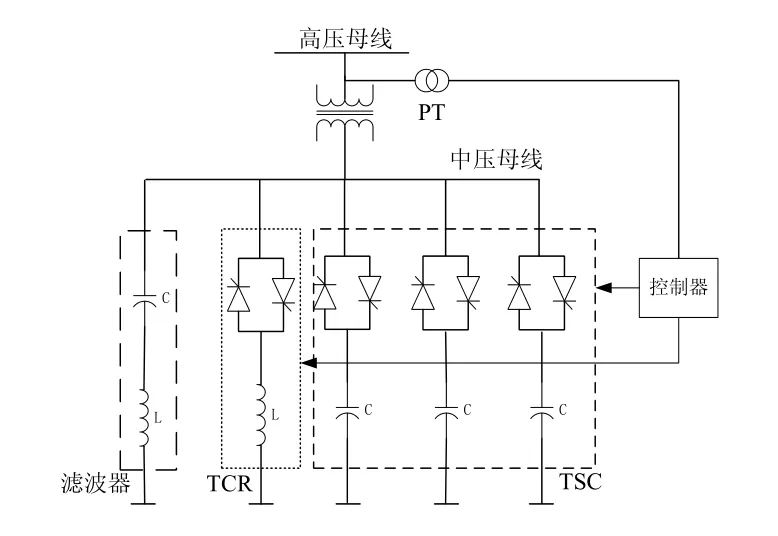
图1 典型静止无功系统

其中，TCR通过控制晶闸管触发角改变其等效并联电抗，其触发角α在～rad之间变化时，基波下TCR的等效电抗XTCR可通过下式计算：

TSC通过晶闸管控制电容的投切。滤波器在基频下为容性，用于滤除TCR产生的谐波。为了实现等效电抗的连续调节，通常TCR的额定容量大于TSC的额定容量。这种SVS通过调节等效电抗来实现对母线电压的控制，并可以进一步起到提高系统的稳定性、增强系统阻尼等作用。

SVS除了上述基于TCR和TSC的结构之外，还包括基于晶闸管投切电抗器(Thyristor Switched Reactor，TSR)和 TSC的 结 构， 以及基于STATCOM的结构，并且这三种结构都可以与机械投切的并联装置（Mechanical Switched Shunt，MSS）进行协调配合。

1.2 SVS的模拟原则

根据研究目的的不同，对SVS进行模拟的详细程度也有所不同。在主要用于系统稳定性分析的机电暂态仿真中，SVS采用基波正序模型。同时，一些对于系统动态行为影响不大的控制和细节可不必在模型中考虑[8]，如：TCR和TSC的电流限制、SVS升压变二次侧电压限制、增益调整器等。此外，对于包含SVC的SVS而言，SVC晶闸管的触发和换相过程相对于机电暂态仿真步长而言是很快的过程，因此可只用一个延时代替，而不进行精确的模拟。同样地，STATCOM中电力电子器件的开关动作也可不进行模拟。

基于SVC的SVS在PSS/E中的表示方法如图2所示，其中SVC的控制器可以进行详细模拟，而SVC的高频特性在仿真中都被忽略。

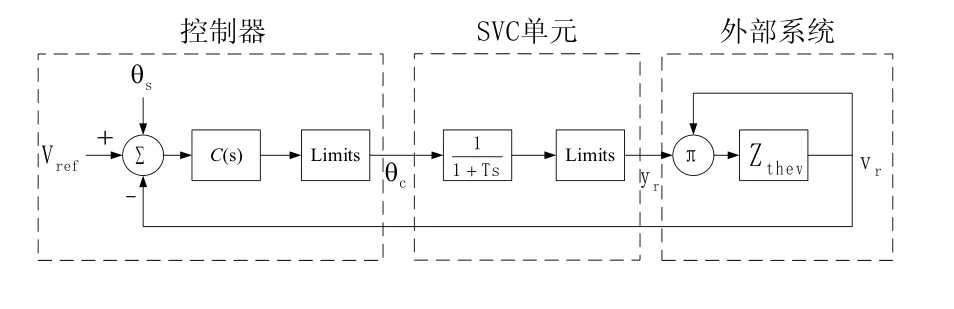
图2 SVC在PSS/E中的表示方法

2 PSS/E中的SVS模型

2.1 潮流模型

PSS/E中包含三种SVS模型（SVSMO1U2、SVSMO2U2和SVSMO3U2），其中基于SVC的SVS模型（SVSMO1U2和SVSMO2U2）在潮流中用可投切并联装置（switched shunt）模拟。两个模型的区别在于包含TCR的SVSMO1U2模型等效电纳可以连续调节；不包含TCR的SVSMO2U2模型等效电纳只能离散变化。SVS所控节点在潮流计算中通常可视为PV节点；当SVS输出达到限幅时，这两种模型都等效为恒定电纳。

基于STATCOM的SVSMO3U2模型在PSS/E中必须采用FACTS模型，以准确模拟其最大输出电流的限制。

2.2 动态模型

PSS/E中的三种SVS模型为通用的时域动态仿真模型，可以在系统规划研究阶段表示SVS一般性的动态行为，但不代表实际控制器的具体实施细节[9]。因此，上述模型具有很强的通用性。此外，这三种SVS模型都可以与MSS进行配合，都可以通过附加控制信号实现附加阻尼控制，在控制结构上有很多的相似之处。以SVSMO1U2模型为例，其整体结构如图3。

三种模型的主要组成部分基本相同。如图3所示，模型包括：测量环节、斜率控制环节、电压调节器（包括超前滞后环节和PI控制环节）、触发延时、稳态输出限制、保护控制策略（低/过电压控制策略、短时过载功能）、MSS的投切逻辑等。

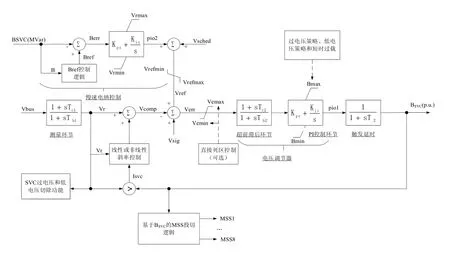
图3 SVSMO1U2模型的控制框

模型中具有三种对SVS稳态输出进行限制的方法，分别为慢速电纳控制、直接死区控制和非线性斜率控制。这三种控制方法都是为了实现当系统电压在设定范围内时，将电流限制在零或零值附近，为后续电压控制或镇定系统保留无功裕度。

慢速电纳控制器缓慢地向SVC参考电压Vsched提供一个偏置，使SVC的输出BSVC回到Bsis和Bscs之间。这一目标通过PI控制器实现。PI控制器输入的Berr需要根据Bref的控制逻辑计算。Bref的控制逻辑如下：

如 果BSVC＜Bsis， 则 令Bref=Bsis+Xeps；如果BSVC＞Bscs，则Bref=Bscs+Xeps；其他情况，Bref=BSVC。

需要注意的是，当BSVC在Bsis和Bscs范围之外时，基于Bsvc的MSS投切逻辑也会动作，使BSVC回到Bsics和Bscs之间。因此，当慢速电纳控制与MSS投切逻辑同时存在时，需要进行协调配合。为了防止两者之间相互影响，需要在慢速电纳控制中设置Xeps这个参数。同时，为了避免MSS过多的动作，慢速电纳调节器应优先动作，因此MSS投切的延时要远大于慢速电纳控制的时间常数。此外，为了不对SVS的电压主控制产生不利影响，慢速电纳控制的时间常数应远大于电压调节器的时间常数。

非线性斜率可以使SVC在给定范围内几乎无响应。SVSMO1U2模型中可以通过参数flag2选择线性或非线性斜率控制。如果flag2参数设置为0，则像其他大多数设计中一样，只有一个标准的线性斜率系数；如果flag2设置为1，则可以实现一个三分段的非线性斜率控制。含有非线性斜率控制的SVC的V-I特性如图4。

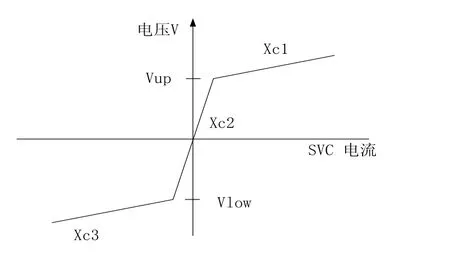
图4 非线性斜率的V-I特性

此外，SVSMO1U2模型还包含可选的直接死区控制。直接死区控制在参考电压Vref附近设定一个电压死区范围：Vref-Vdbd1到Vref+Vdbd1，在电压处于其间时SVC保持输出BSVC不变。其控制逻辑图5。

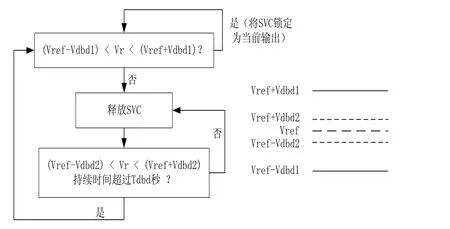
图5 死区控制逻辑

锁定SVC输出表示电压误差Verr被强制为0，同时SVC的输出保持为当前值，直到电压不在指定范围内时释放。释放后，重新锁定SVC输出的条件为电压在更小的范围（Vref－Vdbd2到Vref+Vdbd2）维持一定时间Tdbd。

可见，慢速电纳控制、非线性斜率控制和直接死区控制采用完全不同的方法实现稳态输出限制。因此，为了避免控制上的相互影响，使SVS有稳定和合适的响应效果，PSS/E强烈建议不要将这三种控制中的任意两个组合起来，只能用三个中的一个。

2.3 三种SVS模型对比

SVSMO2U2模型与SVSMO1U2模型的组成结构基本是相同的，但由于SVSMO2U2模型只包含TSC和TSR，其输出是离散的。因此，SVSMO2U2模型的电压调节器输出电纳指令（pio1）后需要经过查询表查找可能的输出，使其尽量接近电纳指令。查询表应包括所有不同输出的TSC/TSR组合。同时，为了避免模型输出在分界点附近时TSC/TSR频繁投切，模型引入了如图6所示的滞回特性。

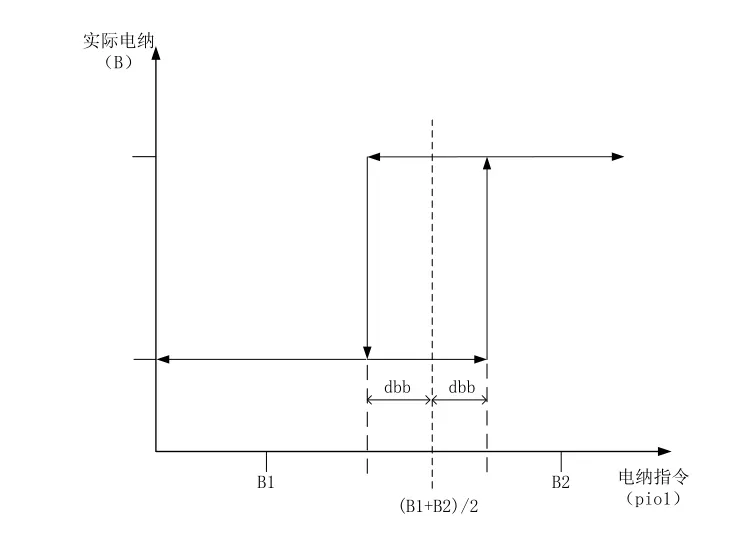
图6 SVSMO2U2模型中电纳变化过程

图中，假设初始电纳输出为B1，之后电压调节器的指令改变，SVC输出保持不变，直到这个指令值超过了B1和B2（下一个可能的离散输出）的平均值加上dbb，此时SVC输出变为B2。由B2变为B1的过程与此相反。这种滞回控制避免了电纳输出的振荡。

SVSMO3U2模型是基于电压源换流器的SVS，核心组成为STATCOM。与基于SVC的SVS不同，当STATCOM达到其无功极限时表现为电流源特性。它与SVSMO1U2模型在电压调节器、超前滞后环节、触发延时环节、斜率控制环节等方面具有相似性，主要区别如下：

1）STATCOM容量通常比较小，因此模型参数基准容量选取为STATCOM的额定容量，而不是与前两个模型相同，为系统基准容量。

2）模型输出为电流，而非电纳。斜率控制、MSS投切逻辑和慢速电流控制器的输入都是模型的输出电流。

3）短时过载有两种选择，其一是允许STATCOM输出短时间内达到Ishrt×Imax1；其二是基于如图7所示的I2t限制。

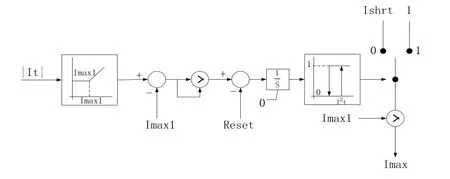
图7 短时过载逻辑

如图所示，当输出电流It超过限值Imax1时，对超过的部分进行时间积分，得到I2t值。当I2t超过设定值时，将输出电流限值在Imax1以下；不超过设定值时，输出电流最大为Ishrt×Imax1。

3 算例分析

3.1 SVS对系统的无功支撑

下面通过算例说明SVS模型对系统的无功支撑作用。采用如图8所示3机9节点系统，将SVS并联于母线9处，并采用SVSMO1U2模型。系统基准容量100MVA。

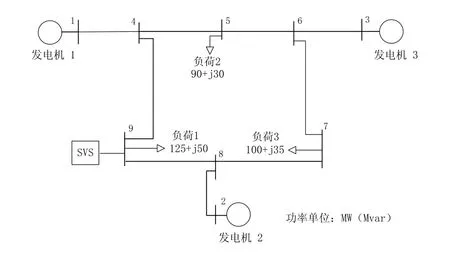
图8 算例系统示意图

采用的SVS结构如图9，包括一个额定容量为45MVA的固定电容器，一个额定容量为25MVA的TCR支路，三个额定容量为20MVA的TSC支路。稳态时保持母线9的电压为1 p.u.，SVS线路潮流见图9。固定电容器向系统注入无功功率45Mvar，一组TSC注入无功功率1.77Mvar，其余支路与系统不交换功率。

在上述潮流计算结果的基础上进行动态仿真。2s时母线4-5之间线路发生三相短路故障，短路阻抗为0。2.1s保护动作切除故障线路。将包含SVS的系统动态响应与母线9仅接有45MVA固定电容器的系统响应进行对比，结果如图10。对含SVS系统，母线9电压和随时间的变化情况如图11，系统中三台发电机无功出力之和与Bsvc随时间的变化情况如图12。

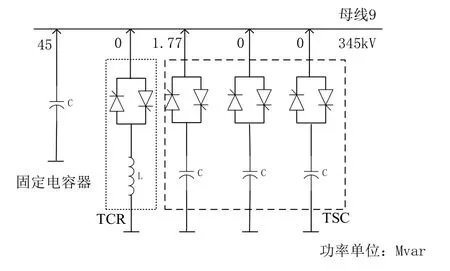
图9 SVS结构图

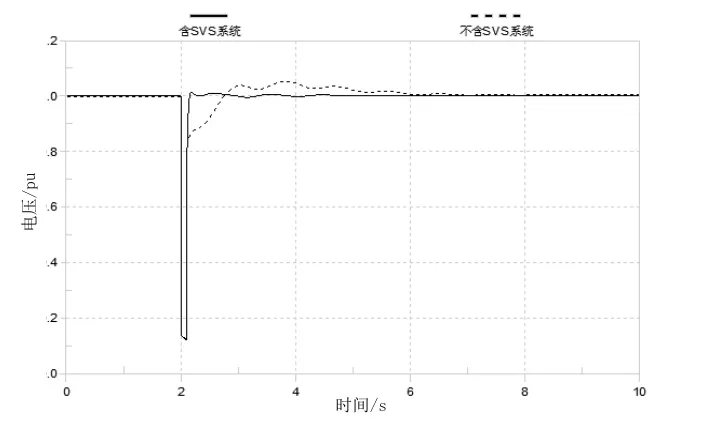
图10 母线9电压对比

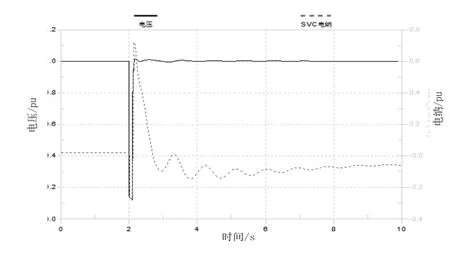
图11 含SVS系统SVC电纳与电压变化

图12 含SVS系统发电机无功出力变化

从图中可以看出，在故障期间，保护控制策略动作，SVS母线电压低于0.3 p.u.时，SVC强制输出为其感性极限-0.25 p.u.。故障线路切除时，SVS母线电压上升到0.6 p.u.以上，SVC在电压调节器的作用下开始输出无功功率，帮助母线电压快速恢复，可以使母线电压在0.1s内恢复到1 p.u.附近。之后，随着发电机无功出力增加，SVC输出电纳逐渐恢复为感性。可见，SVS在故障下可以对系统起到快速的无功支撑作用。

3.2 三种稳态输出限制的控制效果对比

如前所述，SVSMO1U2模型为保证足够的动态无功裕度，可以采用三种不同的控制方法：慢速电纳控制、非线性斜率控制和直接死区控制。为对比这三种方法的控制效果，在3.1节算例系统基础上，分别进行仿真测试。

3.2.1 慢速电纳控制

在2s时将Vsched由1增加到1.02，设置Bscs为10Mvar（0.1p.u.），Bsis为-10Mvar（-0.1p.u.）。有无慢速电纳控制的仿真结果对比如下图。

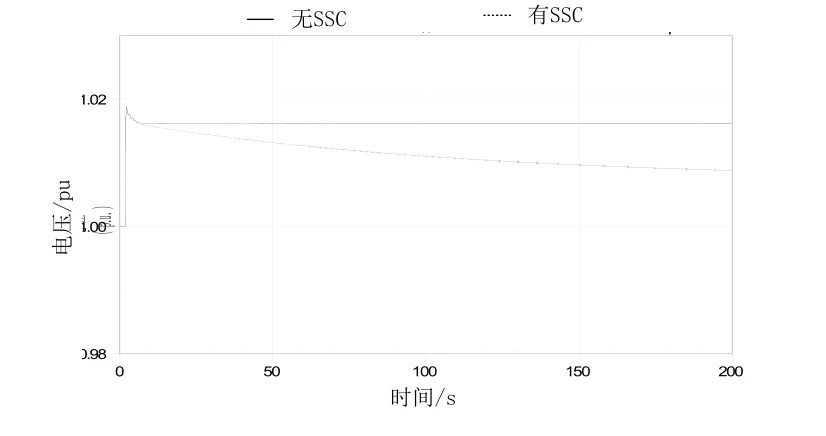
图13 电压变化对比

图14 Bsvc变化对比

可见，在慢速电纳控制起作用之后，SVS输出Bsvc会缓慢减小，以保留更大的动态无功裕度。同时，被控母线电压相比于不采用慢速电纳控制会有一点偏移，与设定的电压值Vsched之间的偏差变大。

3.2.2 三种控制策略对比

为比较三种控制策略的特点，在仿真过程中修改固定电容的数值：稳态时，固定电容器无功功率为45Mvar，仿真到2s时增加10Mvar（变为55Mvar），12s时再增加10Mvar；22s时减小30Mvar，32s时增加10Mvar，恢复到初始状态。对分别采用三种稳态输出控制和无稳态输出限制的仿真结果进行对比，如图15和图16。

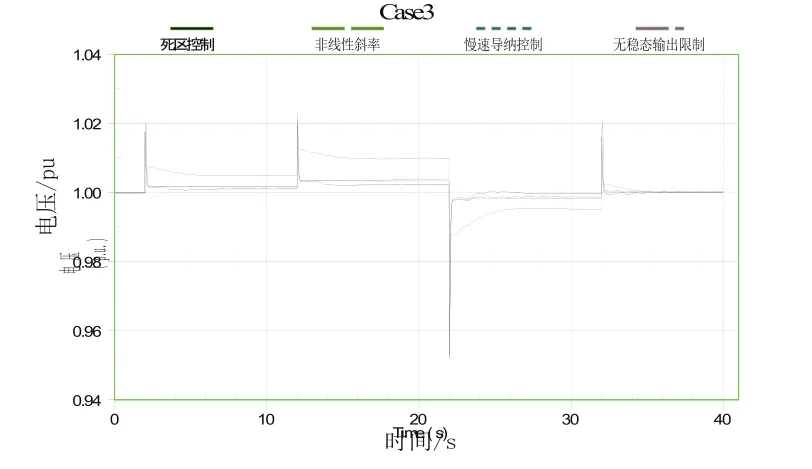
图15 电压变化对比

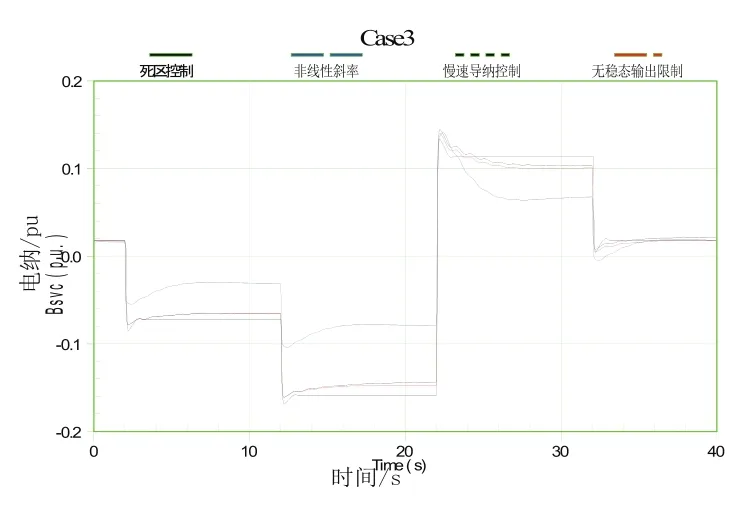
图16 输出电纳对比

由上述仿真结果可以发现，由于慢速电纳控制器的响应时间较长，在仿真中，其母线电压和导纳的变化与无稳态输出限制时很相近。只有当仿真时间足够长时，慢速电纳控制器的作用才会体现出来。慢速电纳控制器的作用总是使SVS输出向零输出靠近，以提高无功裕度。

采用直接死区控制时，当电压在0.99～1.01 p.u.范围内维持1s后，输出Bsvc被锁定不再变化。对比各种策略下的输出导纳可以发现，死区控制在上述仿真条件下无法保证减小SVC输出以维持无功裕度。但若稳态下发生比较小的扰动或增大Vdbd1，使得扰动导致的电压变化不超过Vref－Vdbd1到Vref+Vdbd1的范围，则上述死区控制策略可以维持SVC有较小的输出。因此，可以通过适当增大Vdbd1的范围使死区范围扩大，以保留无功裕度。但另一方面，这将导致电压控制的效果变差，被控母线电压将会在更大的范围内波动。

采用非线性斜率控制时，由于扰动导致的电压变化范围在Vlow到Vup之间，模型的实际反馈系数（斜率）较大（为Xc2）。对比输出导纳可以发现，在Xc2的作用下，SVS的输出电纳变化相比其他策略明显减小，无功裕度更大。但对比电压变化也可以发现，该控制下电压的稳态值距离设定值更远。这一特点与死区控制类似。

综上所述，实际采用具有上述稳态输出限制的控制策略时，一方面需要考虑控制策略的响应时间，以选择合适的控制策略；另一方面要兼顾允许的电压变化范围与动态无功裕度，以确定合理的控制参数。

4 结束语

PSS/E中采用了WECC 推荐的三种SVS通用模型，能够合理模拟实际系统中SVS的动态特性，尤其适用于电力系统稳定性分析。三种SVS模型都包含了电压调节器、MSS投切逻辑、稳态输出限制、保护控制策略等组成结构，在控制上有很多的相似之处。同时，由于三种模型模拟的对象本身特性不同，他们之间在控制和参数上又有一些差别。总体而言，三种模型都具有一定通用性，可以模拟大部分实际的静止无功系统，免去了自定义模型编写的困难与麻烦；三种模型又有一定的灵活性，可以通过修改参数、添加辅助控制环节，以实现提高系统阻尼等作用。

通过算例仿真发现，采用PSS/E中的SVS模型可以快速控制母线电压，提高系统的电压稳定性。模型中包含的慢速电纳控制、非线性斜率控制和直接死区控制策略可以为SVS保证足够的动态无功裕度，但三种策略的实现方式和控制效果有所不同，实际应用中应兼顾响应时间、动态无功裕度和允许的电压变化范围，选择合适的策略和参数。