基于改进PSO-BP神经网络在径流量预测中的应用

王长鹏，齐俊，蔡永宁，杲广文，吴凯

(济南市勘察测绘研究院，山东 济南 250101)

1 引 言

水资源是生产生活中的重要自然资源，河流径流是水文系统的重要内容，河流径流量预测对于汛期防洪、水运灌溉、河流发电等水资源的有效利用起着重要作用[1]。河流径流的生成过程是一个巨大的非线性系统，在建模方面难度较大[2]。同时，河流径流量的影响因素颇多，各项因素的数据单位不统一、数值差异大等客观条件制约，预测系统要求有较好的数据容错能力[3]。构建一个预测精度高、预测速度快的河流径流预测系统，不仅能够完善理论研究，而且对生产实践具有指导意义[4]。

当前，国内外在河流中长期径流量预测这方面的研究还处于摸索阶段，提出了诸多的模型与方法，张利平等在2004年利用4种相空间模型对吉林白山水库的汛期径流量和月径流量进行预测，取得了不错的预测效果[5]。钟平安等在2007年用小波分析法对水库入库径流量进行预测，分析了预测结果与时间、流域等因素的相关关系[6]。王富强等在2009年用多维关联规则数据挖掘算法对嫩江江桥站的汛期径流量进行了预测，结果表明该算法在河流的中长期径流量预测中有良好应用[7]。Kim等在2006年通过对回归模型和神经网络的组合方法对比实验，得出了组合预测方法相较原来的单项预测方法在预测精度上有了提高[8]。Dehuri S等提出了通过粒子群算法优化BP模型预测径流量的一种方法，实验表明两者结合的神经网络算法在预测精度和速度上具备一定的优势[9]。

上述研究具有一定的预测效果，但是，水文系统十分复杂，径流量与降水、蒸发、人类活动等影响因子之间存在着高度的非线性相关性[10]，无法利用单一的数学模型确定建立一个有强大的非线性映射、拟合效果佳的径流量预测模型，反映水文数据规律。

因此，针对河流径流量预测方面的问题，本文进行了深入研究并提出了对应的解决方案，通过优化粒子群算法强大的全局寻优效果来确定BP神经网络最优解的网络连接权值和阈值，优化它在迭代过程中的收敛速度，将改进的混合算法用于训练BP神经网络，并对河流径流量进行预测，用预先准备好未经过训练的数据测试改进后的模型在预测精度上是否有提升。

2 粒子群优化算法的改进

2.1 惯性权重ω的改进

在标准粒子群优化算法(Particle Swarm Optimization，简称PSO算法)中，惯性权重ω决定当前速度相对原有速度的加速程度，能够影响PSO算法的全局搜索和局部搜索能力[11]。由于PSO算法极易早熟，算法后期的时候收敛缓慢，容易在全局最优解附近一直进行寻优，将ω从最大惯性权重值到最小惯性权重值进行递减的方法，来优化问题的最优解寻找[12]。

惯性权重ω的计算公式为：

(1)

在式(1)中，ωset是一个常数值。为了使寻找全局最优解过程中保证有一个合适的收敛速度，设置一个合理的ωset值获取到全局最优解。

在式(1)中，di表示的是第i个粒子到最优粒子之间的由式(2)得到的欧几里得距离：

(2)

在式(2)中，D代表的是每个粒子的问题空间对应的最大维数值，Si，j和Pg，j各自表示的是在第t次的迭代过程中第i个粒子在j维度上的位置值，对应j维位置上最好的粒子，用来求得两个粒子直接的欧几里得距离。dmax和dmin分别代表了粒子群中的所有粒子和最优粒子之间的最大、最小欧几里得距离[13]。当粒子不是当前的最优解时，通过随时间变化的ω值来调节搜索速度，当计算距离变小时，说明离当前的最优粒子越来越近，反之，则说明离当前的最优粒子越来越远。

2.2 加速常数c1，c2的改进

在标准PSO模型中，学习加速常数值c1，c2分别表示每个粒子向pi与pg运动的靠近加速权重数值[14]。通过对粒子当前速度的改变，影响粒子的运动，对粒子目标区域进行搜索，寻找最优解有着重要影响[15]，将加速常数c1，c2从距离最优粒子的平均距离和某维度最大距离的比值随迭代次数变化的方法，来优化问题的最优解寻找。

本文提出了加速常数c1，c2随迭代次数、所有粒子和最优粒子的平均距离与某维度最大距离比值的非线性变化的一种方案，以实现加速常数c1，c2自动变化的目的。加速常数c1，c2的计算公式为：

(3)

(4)

在式(4)中，N代表的是粒子群的粒子数量。

(5)

当初始阶段t较小时，较大的学习常数c1值可以加快粒子群的搜索速度，较快地向全局最优解靠拢；当t逐渐增大时，学习常数c1值随之减小，较大的学习常数c2值可以保证在全局最优解附近搜索而不跳过。

改进后的IPSO算法相较于标准PSO算法在收敛速度上更快，稳定性更高。改进的IPSO算法计算目标函数最优适应值更小，说明预测误差更小，预测的精度更优。

2.3 改进的IPSO算法训练BP神经网络

改进的IPSO算法同标准BP神经网络这两者进行结合，构成IPSO-BP的混合算法模型。在IPSO-BP混合模型训练网络的时候，首先将BP模型的所有连接权值和阈值作为粒子群空间中的各个粒子的位置向量Si，并初始化Si。然后，将BP模型的均方误差值当作每一个粒子的适应度函数值，记录适应值最小值时候的BP模型作为网络的最佳权值和阈值。

改进的IPSO-BP模型的训练步骤流程图如图1所示：

图1 改进IPSO算法训练BP模型步骤流程图

3 IPSO-BP径流量预测模型建立和验证

为了验证训练好的改进IPSO-BP模型预测日径流量，本文以长江干线大埠街至上巢湖段的宜昌水文站所掌握的2008年～2013年的历史日径流量数据对其径流量进行预测。

3.1 数据的采集和预处理

本文所采用的长江干线大埠街至上巢湖段的宜昌水文站2008年～2013年的历史日径流量数据等由武汉市航道局提供。真实数据本身存在噪声数据，而且不利于直接用改进的IPSO-BP结构模型直接进行径流量真实数值的预测。对原始数据进行预处理，确保为改进的IPSO-BP神经网络模型提供准确、适当的特征值，提高预测的准确度。将历史径流量数据分为两部分，一部分为训练数据，用来训练改进的IPSO-BP神经网络，剩余数据用来测试IPSO-BP结构模型，用它的预测效果与真实值进行对比。

对数据的预处理操作主要包含数据的降噪处理、数据时序化处理以及数据归一化处理等内容。

神经网络结构中归一化输入层的输入参数一般通过以下公式进行：

(6)

式(6)中y为输入数据归一化后的参数值；x为输入数据，是经过降噪处理和时序化后的实际数据；xmax为该输入参数的最大实际数据的数值；xmin为该输入参数的最小实际数据的数值。

将河流水位、流速、降水量和温度数据归一化后的部分结果数据如表1所示：

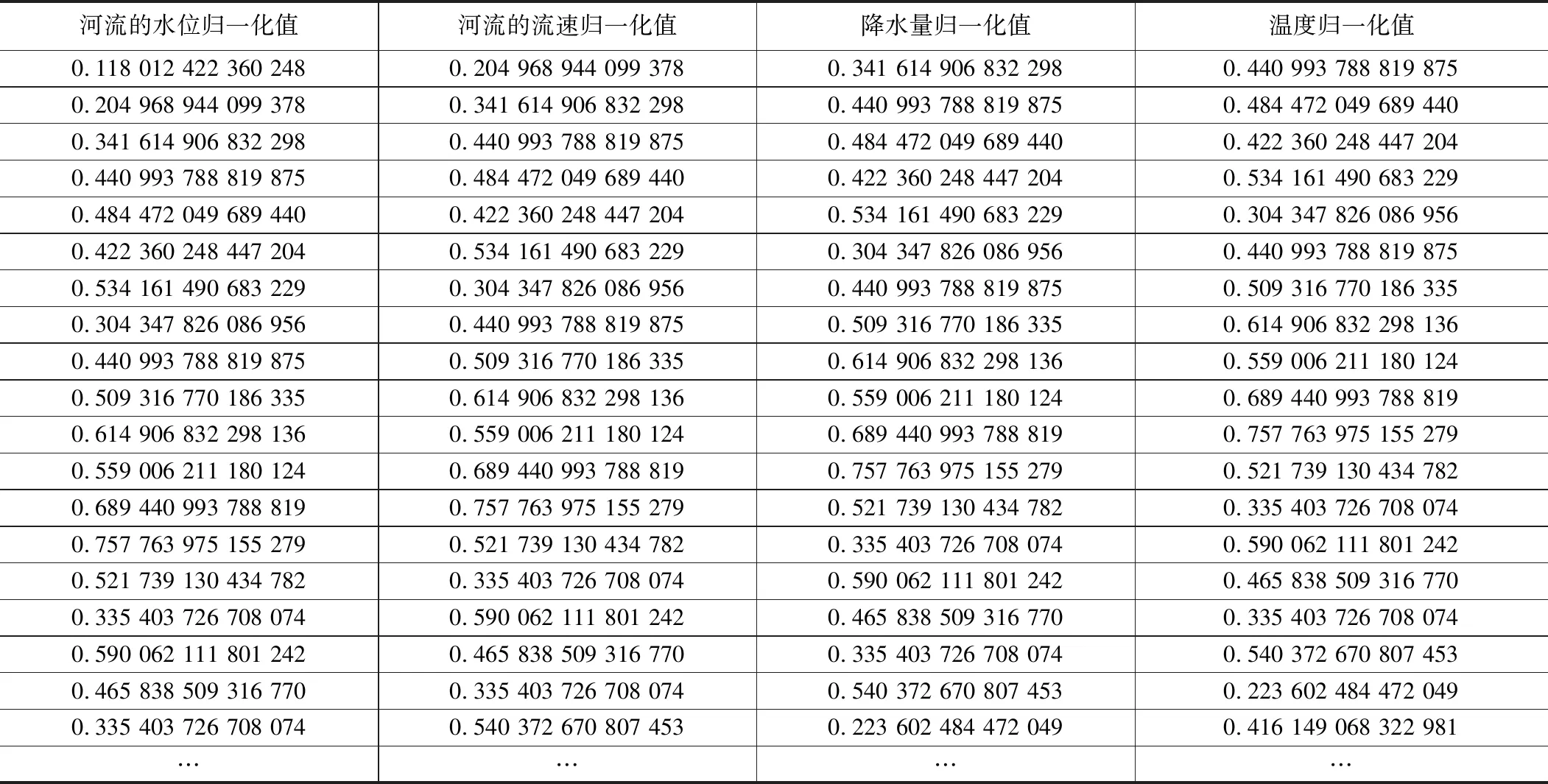
输入数据归一化表 表1

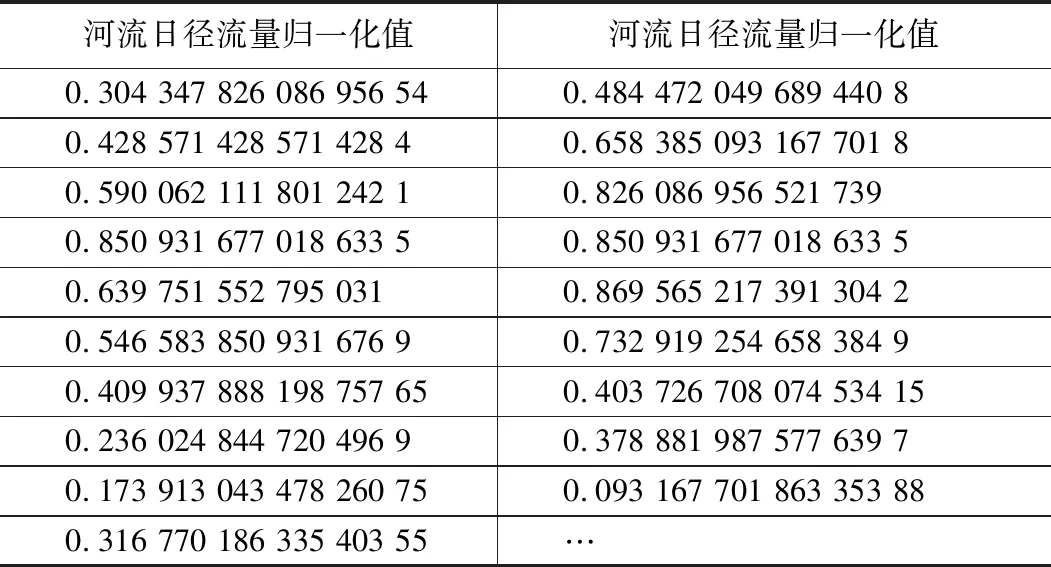
输出数据归一化表 表2

表1的输入数据归一化表和表2的输出数据归一化表，表明数据预处理成功，实验数据已经准备完毕，可以进行下一步的模型验证。

3.2 改进的IPSO-BP模型进行预测和评估

在将实验数据进行预处理后，将它们用来进行神经网络模型的训练，剩下连续的90天数据为测试数据样本，用来验证训练好的神经网络模型的可靠性和预测能力。

用实验数据分别使用的标准BP神经网络模型、标准PSO-BP神经网络模型和改进IPSO-BP神经网络模型对数据进行了训练和验证。

通过预测的精度和模型的收敛速度两方面来对这3个模型进行了对比分析。日径流量预测的精度通过预测径流量与实际径流量的误差比较来衡量，分别比较误差值小于3%和误差值小于5%的统计样本数占总测试样本数的比例来进行判断预测精度的好坏。

如图2所示，为训练好的改进IPSO-BP模型对日径流量进行的预测。

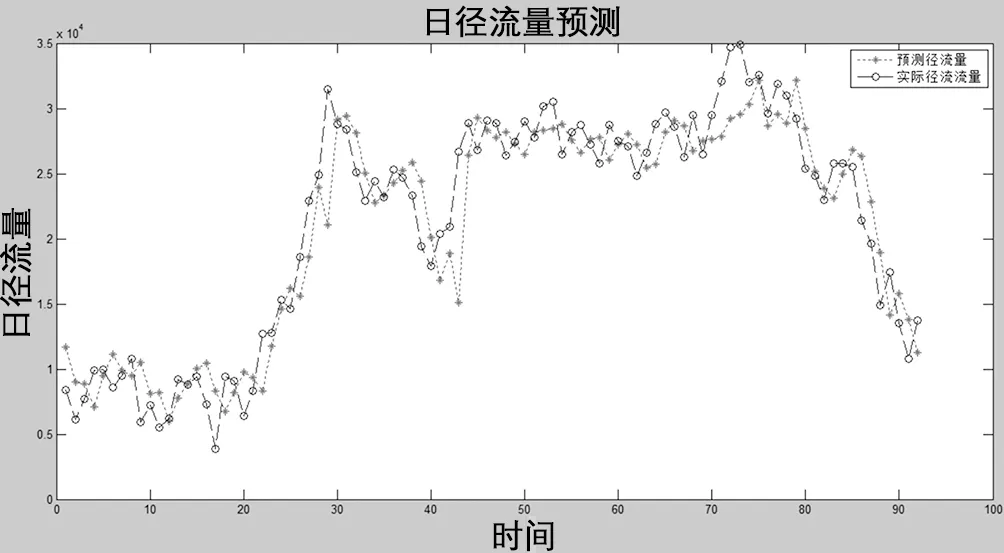
图2 改进的IPSO-BP模型预测日径流量

如图3所示，为训练好的改进IPSO-BP日径流量预测模型所对应的预测均方误差曲线。

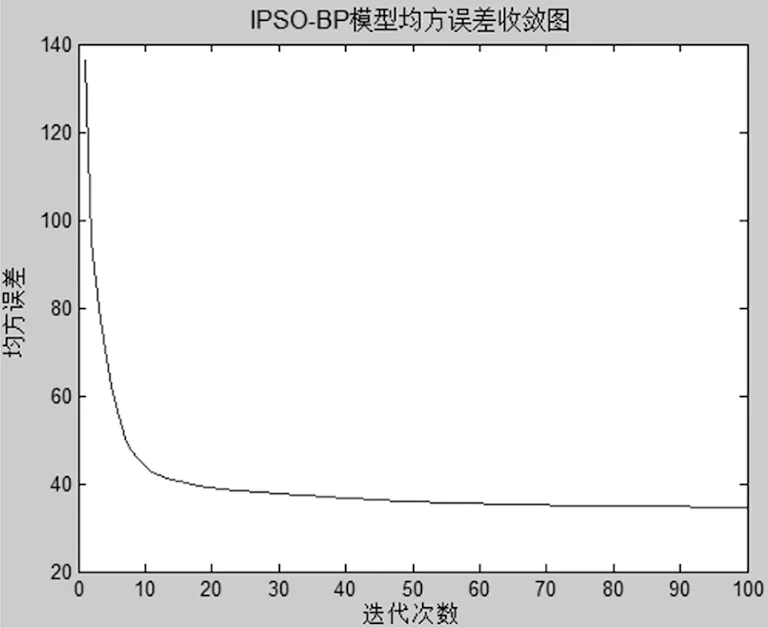
图3 改进的IPSO-BP神经网络误差曲线

如图4所示，为标准BP神经网络模型、标准PSO-BP神经网络模型和本文提出的改进IPSO-BP神经网络模型的算法均方误差的收敛速度快慢比较。

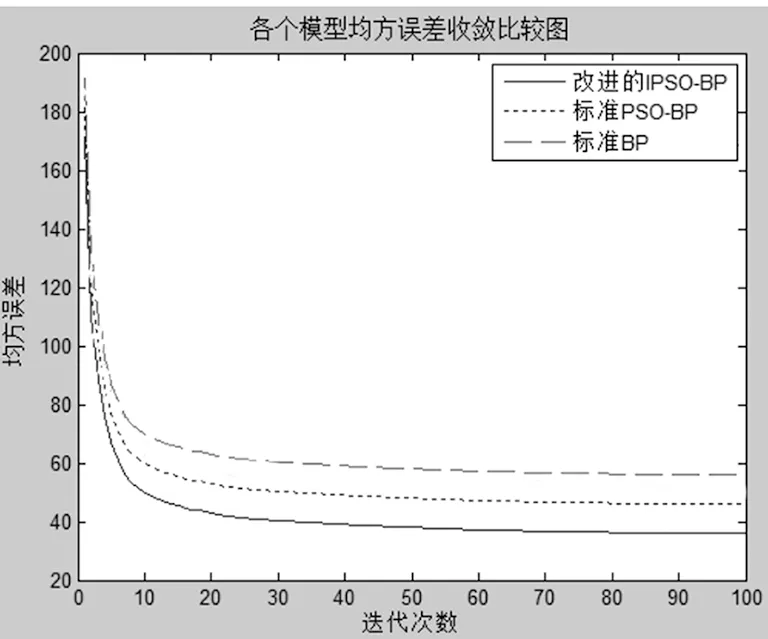
图4 改进的IPSO-BP模型和各种模型的均方误差比较

通过图4，我们可以清楚地看出各种模型的迭代收敛速度，其中改进的IPSO-BP神经网络模型相较于其他2种算法模型在收敛速度方面有着明显优势。

因此，在保证神经网络模型的收敛速度确实占优的同时，我们还要验证改进后IPSO-BP神经网络是否在预测结果误差精度值上面相较于其他模型有明显改善。

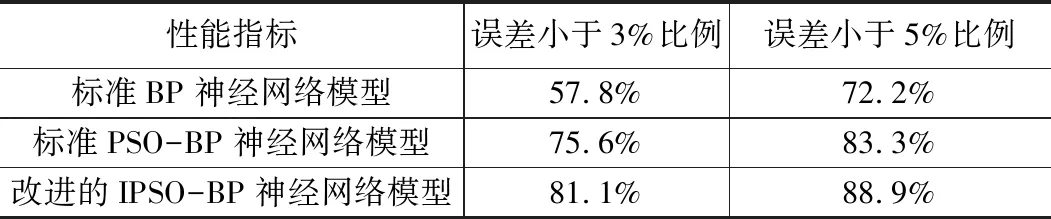
各个模型性能比较表 表3

通过表3各个模型性能对比表，我们可以看出，在各个误差精度相同的条件下，3种模型的性能指标比较中，改进后IPSO-BP神经网络模型在同样的误差指标下面拥有更高的成功收敛数量百分比，说明它在预测精度方面明显拥有更高的精确性。

通过实验对比3种神经网络模型，我们能够从中得到相应的结论：改进的IPSO-BP神经网络模型在河流的日径流量预测中，它的全局搜索能力明显改善，在搜索速度方面也有了较大的提升，同时，在此基础上它还保证了算法预测的精度要求。因此，可以说改进的IPSO-BP神经网络模型算法，确实是优于标准BP神经网络算法以及标准的PSO-BP神经网络算法。

4 总 结

通过动态调节惯性权重和学习加速常数来改变粒子群的粒子速度和位置，将改进的IPSO算法和BP神经网络结构模型相结合，建立改进后IPSO-BP神经网络模型，通过历史真实数据对模型进行训练，利用训练好的模型对宜昌水文站的日径流量数据进行预测，改进后IPSO-BP神经网络模型在收敛的速率方面和预测的误差精度方面都比其他两种算法模型有显著优势。由于受客观因素和作者水平的限制，在河流日径流预测方面还存在着很多的不足，需要以后进行更加深入的研究，提出更加完善的预测模型或预测方法。